الگوریتم ژنتیک – از صفر تا صد
الگوریتم ژنتیک (GA | Genetic Algorithms)، خانوادهای از «مدلهای محاسباتی» (Computational Models) است که از مفهوم «تکامل» (Evolution) الهام گرفته شدهاند. این دسته از الگوریتمها، «جوابهای محتمل» (Potential Solutions) یا «جوابهای کاندید» (Candidate Solutions) و یا «فرضیههای محتمل» (Possible Hypothesis) برای یک مسأله خاص را در یک ساختار دادهای «کروموزوم مانند» (Chromosome-like) کدبندی میکنند. الگوریتم ژنتیک از طریق اعمال «عملگرهای بازترکیب» (Recombination Operators) روی ساختارهای دادهای کروموزوم مانند، اطلاعات حیاتی ذخیره شده در این ساختارهای دادهای را حفظ میکند.


در بسیاری از موارد، از الگوریتمهای ژنتیک به عنوان الگوریتمهای «بهینهساز تابع» (Function Optimizer) یاد میشود؛ یعنی، الگوریتمهایی که برای بهینهسازی «توابع هدف» (Objective Functions) مسائل مختلف به کار میروند. البته، گستره کاربردهایی که از الگوریتم ژنتیک، برای حل مسئله در دامنه کاربردی خود استفاده میکنند، بسیار وسیع است.
پیادهسازی الگوریتم ژنتیک، معمولا با تولید جمعیتی از کروموزومها (جمعیت اولیه از کروموزومها در الگوریتمهای ژنتیک، معمولا تصادفی تولید میشود و مقید به حد بالا و پایین متغیرهای مسأله هستند) آغاز میشود. در مرحله بعد، ساختارهای دادهای تولید شده (کروموزومها) «ارزیابی» (Evaluate) میشوند و کروموزومهایی که به شکل بهتری میتوانند «جواب بهینه» (Optimal Solution) مسأله مورد نظر (هدف) را نمایش دهند، شانس بیشتری برای «تولید مثل» (Reproduction) نسبت به جوابهای ضعیفتر پیدا میکنند. به عبارت دیگر، فرصتهای تولید مثل بیشتری به این دسته از کروموزومها اختصاص داده میشود. میزان «خوب بودن» (Goodness) یک جواب، معمولا نسبت به جمعیت جوابهای کاندید فعلی سنجیده میشود.

مقدمه
بسیاری از اختراعات بشری از طبیعت الهام گرفته شدهاند. «شبکههای عصبی مصنوعی» (ANN | Artificial Neural Network) نمونه بارز چنین ابداعاتی هستند. یکی دیگر از چنین ابداعاتی، توسعه ایده الگوریتم ژنتیک است. الگوریتمهای ژنتیک، با «شبیهسازی» (Simulating) فرایند تکامل در طبیعت، با هدف یافتن بهترین جواب ممکن برای یک مسأله، به جستجو در «فضای جوابهای کاندید» (Candidate Solution Space) میپردازند.
در فرایند جستجو برای یافتن جواب بهینه، ابتدا مجموعه یا جمعیتی از جوابهای ابتدایی تولید میشود. سپس، در «نسلهای» (Generations) متوالی، مجموعهای از جوابهای تغییر یافته تولید میشوند (در هر نسل از الگوریتم ژنتیک، تغییرات خاصی در ژنهای کروموزومهای تشکیل دهنده جمعیت ایجاد میشود). جوابهای اولیه معمولا به شکلی تغییر میکنند که در هر نسل، جمعیت جوابها به سمت جواب بهینه «همگرا» (Converge) میشوند.
این شاخه از حوزه «هوش مصنوعی» (Artificial Intelligence)، بر پایه مکانیزم تکامل موجودات زنده و تولید گونههای موفقتر و برازندهتر در طبیعت الهام گرفته شده است. به عبارت دیگر، ایده اصلی الگوریتمهای ژنتیک، «بقای برازندهترینها» (Survival of the Fittest) است.
یک کروموزوم، رشتهای بلند و پیچیده از «اسید دیاکسی ریبونوکلئیک» (Deoxyribonucleic Acid) یا DNA است. عوامل ارثی که ویژگیها یا خصیصههای یک «فرد» (Individual) را مشخص میکنند، در طول این کروموزومها نقش یافتهاند. هر یک از خصیصههای موجود در افراد، به وسیله ترکیبی از DNA، در ژنهای انسان کدبندی میشوند. در بدن موجودات زنده، معمولا چهار «پایه» (Base) برای تولید کروموزومها از روی DNA وجود دارد:
- پایه A یا Adenine
- پایه C یا Cytosine
- پایه G یا Guanine
- پایه T یا Thymine
همانطور که الفبا، واحدهای سازنده یک «زبان» (Language) را تعریف میکند، ترکیب با معنی از کروموزومها (و پایههای آنها)، دستورالعملهای خاصی را برای سلولها تولید میکند. تغییرات در کوروموزومها، طی فرایند تولید مثل اتفاق میافتد. کروموزومهای «والدین» (Parents) از طریق فرایند خاصی به نام «ترکیب یا آمیزش» (Crossover)، به طور تصادفی با یکدیگر مبادله میشوند. بنابراین، فرزندان برخی از ویژگیها یا خصیصههای پدر و برخی از ویژگی یا خصیصههای مادر را به ارث میبرند و از خود به نمایش میگذارند.
فرایند نادری به نام «جهش» (Mutation) نیز سبب ایجاد تغییراتی در ویژگیها یا خصیصههای موجودات زنده میشود. برخی از مواقع، ممکن است خطایی در فرایند کپی کردن کروموزومها رخ دهد که به آن «میتوز» (Mitosis) نیز گفته میشود. غالب جهشهایی که در موجودات زنده اتفاق میافتد، منجر به از بین رفتن موجودات خواهد شد؛ با این حال، در یک دوره چند میلیون ساله از تکامل، جهش ممکن است منجر به ایجاد گونههای جدید و برازندهتر از موجودات زنده شود.

انتخاب طبیعی
در طبیعت، موجوداتی که ویژگیهای برازندهتری نسبت به دیگر گونهها دارند، برای مدت بیشتری به بقاء در طبیعت ادامه میدهند. چنین ویژگیای، این امکان را در اختیار برازندهترین موجودات زنده قرار میدهد تا بر اساس مواد ژنتیکی خود، اقدام به تولید مثل کنند. بنابراین، پس از یک دوره زمانی بلند مدت، جمعیت موجودات زنده به سمتی تکامل پیدا خواهد کرد که در آن، غالب موجودات بسیاری از ویژگیهای ارثی خود را از «ژنهای» (Genes) موجودات برتر و تعداد کمی از ویژگیهای خود را از ژنهای موجودات «رده پایین» (Inferior) با ژنها یا ویژگیهای نامرغوب به ارث خواهند برد.
به بیان سادهتر، موجودات برازندهتر زنده میمانند و موجودات نامناسب از بین میروند. به این فرایند و نیروی شگفتانگیز طبیعی، «انتخاب طبیعی» (Natural Selection) گفته میشود. نکته مهم در مورد انتخاب طبیعی و اثبات درست بودن این اصل این است که تحقیقات دانشمندان در مورد «توضیحات مولکولی از تکامل» (Molecular Explanation of Evolution) نشان داده است که گونههای مختلف موجودات زنده، خود را با شرایط محیطی تطبیق نمیدهند، بلکه صرفا موجودات برازندهتر به بقاء خود ادامه میدهند.
با توجه به اهمیت روشهای بهینهسازی هوشمند و الگوریتمهای تکاملی، «فرادرس» اقدام به انتشار فیلم آموزش تئوری و عملی الگوریتم ژنتیک در قالب آموزشی ۱۴ ساعت و ۲۳ دقیقهای کرده که در ادامه متن به آن اشاره شده است.
- برای دیدن فیلم آموزش تئوری و عملی الگوریتم ژنتیک + اینجا کلیک کنید.
تکامل شبیهسازی شده
برای شبیهسازی فرایند انتخاب طبیعی توسط سیستمهای کامپیوتری و حل مسأله با استفاده از الگوریتمهای الهام گرفته شده از انتخاب طبیعی، ابتدا باید مدلهای نمایشی جهت مدلسازی متغیرهای مسأله تعریف شوند:
- نمایشی از یک «موجودیت» (Individual) در هر نقطه از فضای جستجوی مسأله در طول فرایند جستجو برای یافتن جواب بهینه: برای چنین کاری، مفهوم «نسلهای» (Generation) متوالی از موجودیتها مطرح میشود. هر موجودیت یک ساختار دادهای خواهد بود که «ساختار ژنتیکی» (Genetic Structure) یک جواب یا فرضیه محتمل/کاندید را نمایش میدهد. همانند یک کروموزوم، ساختار ژنتیکی یک موجودیت توسط الفبایی ثابت و محدود توصیف خواهد شد. به عنوان نمونه، الگوریتم ژنتیک از الفبای مبتنی بر رشتههای «باینری» (Binary)، «مقادیر صحیح» (Integer Values) یا «مقادیر حقیقی» (Real Values) به عنوان تفسیری از جوابهای محتمل برای یک مسأله خاص استفاده میکند.
به عنوان نمونه، مسأله «فروشنده دورهگرد» (Travelling Salesman) یا TSP را در نظر بگیرید. مسأله فروشنده دورگرد، مسأله پیدا کردن مسیر بهینه برای پیمایش مثلا 10 شهر است. فروشنده میتواند مسیر پیمایشی خود را از هر شهری شروع کند. بنابراین، جوابهای این مسأله «جایگشتی» (Permutation) از شهرهای پیمایش شده خواهد بود: 1-3-2-5-4-8-10-9-7-8-6.
فرهنگ لغات الگوریتم ژنتیک
در ادامه، برخی از اصطلاحات و واژگان کلیدی در توصیف فرایندهای موجود در الگوریتم ژنتیک نمایش داده شده است. نکته مهم در مورد فرهنگ لغات الگوریتم ژنتیک این است که اصطلاحات و واژگان کلیدی مترادف و معادل یکدیگر، در زمینههای موضوعی مرتبط با الگوریتم ژنتیک، غالبا به جای یکدیگر مورد استفاده قرار میگیرند.
| الگوریتم ژنتیک | توضیح |
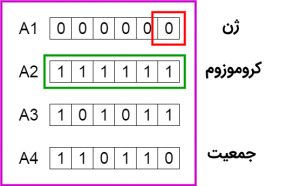
| کروموزوم (رشته، موجودیت) | جواب مسأله |
| ژنها (بیتها) | بخشی از جواب مسأله |
| مکان (Locus) | مکان ژنها |
| آللها (Alleles) | مقادیر ژنها |
| فنوتایپ (Phenotype) | جواب کدگشایی شده مسأله |
| ژنوتایپ (Genotype) | جواب کدبندی شده مسأله |
الگوریتم ژنتیک متعارف
در ادامه، با مؤلفههای اساسی الگوریتمهای ژنتیک و نحوه عملکرد آنها در پیدا کردن جواب بهینه یک مسأله خاص مورد بررسی قرار میگیرد.
مفاهیم مهم ابتدایی در الگوریتم ژنتیک
الگوریتمهای ژنتیک، الگوریتمهای جستجو هستند که بر پایه مفاهیم انتخاب طبیعی و ژنتیک موجودات زنده بنا نهاده شدهاند. الگوریتمهای ژنتیک پدیده آمدهاند تا برخی از فرایندهای مشاهده شده در «تکامل طبیعی» (Natural Evolution) را از طریق الگوریتمهای کامپیوتری شبیهسازی کنند. فرایندهایی که بر اساس انجام عملیات روی کروموزومها (سیستمهای ارگانیک جهت کدبندی کردن ساختار ژنتیکی موجودات زنده) شکل گرفتهاند.
همانطور که پیش از این نیز اشاره شد، الگوریتمهای ژنتیک در زیر مجموعه الگوریتمهای جستجو قرار میگیرند. با این حال، تفاوتهای بسیار اساسی با دیگر الگوریتمهای جستجو دارند. الگوریتمهای ژنتیک به جای اینکه به طور مستقیم با مقادیر پارامترهای مسأله سروکار داشته باشند، با نمایشی کدبندی شده از مجموعه پارامترهای مسأله کار میکنند و جمعیتی متشکل از نقاط در یک فضای جستجو را برای یافتن جوابهای مسأله جستجو میکنند. همچنین، بدون اینکه از اطلاعات «گرادیان» (Gradient) مرتبط با «تابع هدف» (Objective Function) مسأله اطلاعی داشته باشند، تابع هدف مسأله را بهینهسازی میکنند.
در الگوریتمهای ژنتیک برای «گذار» (Transition) از یک حالت در فضای مسأله به حالت دیگر، از مکانیزمهای «احتمالی» (Probabilistic) استفاده میشود؛ در حالی که در الگوریتمهای جستجوی مرسوم، از اطلاعات گرادیان مرتبط با تابع هدف مسأله برای چنین کاری استفاده میشود. چنین ویژگی مهمی در الگوریتمهای ژنتیک، آنها را تبدیل به الگوریتمهای جستجوی «همه منظوره» (General purpose) کرده است. همچنین، از الگوریتمهای ژنتیک برای جستجوی فضاهای جستجوی نامنظم و بیقاعده استفاده میشود. به طور کلی، از الگوریتمهای ژنتیک برای حل مسأله در کاربردهایی نظیر بهینهسازی توابع، «تخمین پارامتر» (Parameter Estimation) و «یادگیری ماشین» (Machine Learning) استفاده میشود.

اصول ابتدایی در الگوریتم ژنتیک
اصول کاری الگوریتم ژنتیک، در ساختار الگوریتمی زیر نمایش داده شده است. مهمترین گام لازم برای پیادهسازی الگوریتم ژنتیک و انواع مختلف آن عبارتند از: تولید جمعیت (اولیه) از جوابهای یک مسأله، مشخص کردن تابع هدف، تابع «برازندگی» (Fitness) و به کار گرفتن «عملگرهای ژنتیک» (Genetic Operators) جهت ایجاد تغییرات در جمعیت جوابهای مسأله. عملگرهای ژنتیک قابل تعریف در الگوریتم ژنتیک، در ادامه معرفی خواهند شد. اصول کاری الگوریتم ژنتیک عبارتست از:
- فرموله کردن جمعیت ابتدایی متشکل از جوابهای مسأله
- مقداردهی اولیه و تصادفی جمعیت ابتدایی متشکل از جوابهای مسأله
- حلقه تکرار:
- ارزیابی تابع هدف مسأله
- پیدا کردن تابع برازندگی مناسب
- انجام عملیات روی جمعیت متشکل از جوابهای مسأله با استفاده از عملگرهای ژنتیک
- عملگر «تولید مثل» (Reproduction)
- عملگر «ترکیب یا آمیزش» (Crossover)
- عملگر «جهش» (Mutation)
- تا زمانی که: شرط توقف ارضا شود.
یکی از مهمترین ویژگیهای الگوریتم ژنتیک، کدبندی متغیرهای لازم برای توصیف مسأله است. مرسومترین روش کدبندی متغیرهای مسأله، تبدیل متغیرها به رشته یا برداری از مقادیر باینری، صحیح و یا حقیقی است. بهترین عملکرد الگوریتمهای ژنتیک معمولا زمانی اتفاق میافتد که از نمایش باینری برای کدبندی متغیرهای مسأله استفاده میشود.
اگر مسألهای که قرار است جوابهای بهینه آن مشخص شود بیش از یک متغیر داشته باشد، به تعداد متغیرهای آن مسأله، «کدبندیهای تک متغیره» (Single-Variable Coding) متناظر با تک تک آنها ایجاد و با یکدیگر ادغام میشوند. در چنین حالتی، یک «کدبندی چند متغیره» (Multi-Variable Coding) از مسأله مورد نظر شکل خواهد گرفت. یکی از مهمترین ویژگیهای الگوریتمهای ژنتیک، پردازش همزمان چندين جواب کاندید تولید شده برای مسأله تعریف شده است.
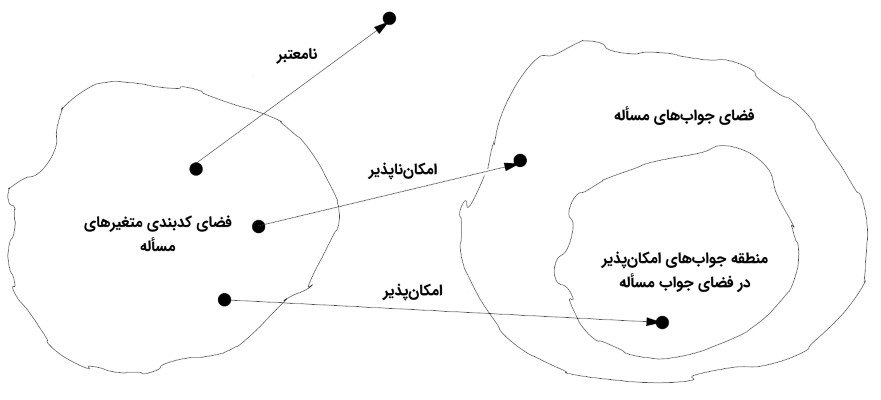
بنابراین، در مرحله اول از پیادهسازی الگوریتم ژنتیک، مجموعهای متشکل از P موجودیت یا کروموزوم توسط «مولدهای شبه تصادفی» (Pseudo Random Generators) تشکیل میشود. هر کدام از موجودیتها با کروموزومهای موجود در این جمعیت، یک جواب کاندید و امکانپذیر برای مسأله را نمایش میدهند. هر کدام از این موجودیتها، یک نمایش برداری از جواب مسأله در یک «فضای جواب» (Solution Space) هستند که به آنها «جواب اولیه» (Initial Solution) نیز گفته میشود.
از آنجایی که عملیات جستجو از مجموعهای از جوابها (جوابهای اولیه به طور تصادفی در فضای جواب پراکنده شدهاند) در فضای جواب مسأله آغاز میشود، جستجوی قدرتمند و بدون بایاس در الگوریتم ژنتیک تضمین خواهد شد. در مرحله بعد، تمامی جوابهای اولیه تولید شده مورد ارزیابی قرار میگیرند تا مقدار تابع هدف هر کدام از آنها مشخص شود.
در این مرحله، معمولا یک «تابع جریمه خارجی» (Exterior Penalty Function) به کار گرفته میشود تا «مسأله بهینهسازی مقید» (Constrained Optimization Problem) به یک مسأله بهینهسازی «نامقید» (Unconstrained) تبدیل شود. چنین تبدیلی، بسته به مسائل بهینهسازی مختلف (مسائلی که قرار است جوابهای بهینه آنها تولید شود)، متفاوت خواهد بود.
در مرحله سوم، تابع هدف مسأله به یک تابع برازندگی نگاشت میشود. از طریق تابع برازندگی، «مقدار برازندگی» (Fitness Value) هر یک از اعضای جمعیت اولیه مشخص میشود. پس از مشخص شدن مقدار برازندگی جوابهای کاندید، از عملگرهای الگوریتم ژنتیک جهت انجام تغییرات روی جوابهای کاندید استفاده میشود.
اصول کاری الگوریتم ژنتیک
برای نمایش اصول کاری الگوریتم ژنتیک، یک مسأله بهینهسازی نامقید در نظر گرفته میشود. فرض کنید که مسأله بهینهسازی زیر داده شده است و هدف الگوریتم ژنتیک، «بیشینهسازی» (Maximizing) تابع زیر باشد:
در این رابطه، و حد بالا و حد پایین تعیین شده برای مقادیر متغیر است. اگر چه در اینجا از یک مسأله بیشینهسازی برای نمایش اصول کاری الگوریتم ژنتیک استفاده است، با این حال، الگوریتم ژنتیک به راحتی قادر به کمینهسازی مسائل مختلف نیز خواهد بود. برای پیادهسازی الگوریتمهای ژنتیک، وظایف خاصی باید تعریف و توسط این الگوریتم، جهت بهینهسازی توابع مختلف، اجرا شوند.
کدبندی متغیرهای مسأله
برای اینکه الگوریتم ژنتیک قادر باشد تا تابع بالا را بیشینه کند، متغیرهای باید توسط یک ساختار رشتهای کدبندی شوند. شایان توجه است که کدبندی متغیرهای مسأله، کاملا ضروری نیست. در تحقیقات انجام شده توسط محققان این حوزه، الگوریتمهای ژنتیکی پیادهسازی شدهاند که به جای کدبندی متغیرهای مسأله، به طور مستقیم روی خود متغیرها عمل میکنند. با این حال، این دسته از الگوریتمها به نوعی استثناء محسوب میشوند و در این مطلب، کدبندی متغیرهای مسأله به عنوان یکی از وظایف اصلی الگوریتمهای ژنتیک مرسوم لحاظ شده است.
از کدبندی مبتنی بر رشتههای باینری، برای کدبندی متغیرهای مسأله استفاده میشود. در الگوریتم ژنتیک، طول رشته باینری معمولا بر حسب دقت مطلوب و مورد انتظار از مسأله بهینهسازی تعیین میشود. به عنوان نمونه، اگر از چهار بیت برای کدبندی یک مسأله بهینهسازی دو متغیره استفاده شود، رشتههای (0000 0000) و (1111 1111) به ترتیب متناظر با دو نقطه و در فضای جواب مسأله خواهند بود؛ زیرا، زیررشتههای (0000) و (1111) حد بالا و پایین یک نقطه در فضای جستجوی مسأله را نمایش خواهند داد.
در کدبندی متغیرهای مسأله، با استفاده از یک «قانون نگاشت» (Mapping Rule) ثابت، هر رشته هشت بیتی را میتوان به یک نقطه در فضای جستجوی مسأله نگاشت کرد. معمولا از قانون نگاشت خطی زیر، برای نگاشت یک رشته هشت بیتی به یک نقطه در فضای جستجوی مسأله استفاده میشود:
در این رابطه، متغیر به وسیله زیر رشته با طول کدبندی شده است. مقدار کدگشایی شده زیر رشته ، از طریق عبارت محاسبه میشود. همچنین، به وسیله مقادیر (0 ، 1) و رشته ، در قالب نمایش داده میشوند. به عنوان نمونه، با استفاده از رابطه ، مقدار کدگشایی شده برای رشته چهار بیتی (0111)، برابر با مقدار 7 محاسبه خواهد شد.
شایان توجه است که برای یک رشته 4 بیتی، از آنجایی که هر بیت تنها میتواند مقادیر 0 یا 1 به خود اختیار کند، تنها 16 زیر رشته متمایز قابل تعریف خواهد بود. دقت قابل استحصال توسط کدبندی چهار بیتی، تقریبا برابر با یک شانزدهم (1/16) فضای جستجوی مسأله است. اما اگر طول رشته به 5 افزایش پیدا کند، دقت قابل استحصال توسط کدبندی پنج بیتی، تقریبا برابر با یک سی و دوم (1/32) فضای جستجوی مسأله خواهد شد.
بنابراین، طول زیر رشتههای نمایش دهنده مقادیر متغیرها، وابستگی مستقیم به دقت مطلوب و مورد انتظار از متغیرها دارد. طول زیر رشتهها، بسته به دقت مطلوب و مورد انتظار از نتایج الگوریتم، متغیر است؛ هر چقدر طول رشتهها بیشتر باشد، دقت نتایج خروجی بیشتر میشود. رابطه میان طول رشته و دقت نتایج تولید شده از طریق رابطه زیر به دست میآید:
به محض اینکه فرایند کدبندی متغیرهای مسأله به پایان رسید، هر کدام از نقاط متناظر با مقادیر متغیرهای مسأله، ، تولید و در فضای جستجوی مسأله قرار داده خواهند شد. پس از تولید نقاط متناظر با مقادیر متغیرهای مسأله در فضای جستجو، مقدار تابع در نقطه ، از طریق جایگذاری در یک تابع هدف داده شده یا همان ، محاسبه خواهد شد.
تابع برازندگی
همانطور که پیش از این نیز اشاره شد، الگوریتم ژنتیک از اصل بقاء برازندهترینها در طبیعت، برای ایجاد فرایند جستجو و متعاقبا، جستجو در فضای جواب مسأله استفاده میکند. بنابراین، الگوریتم ژنتیک برای حل مسائل بهینهسازی (بیشینهسازی یا کمینهسازی) بسیار مناسب خواهد بود. به طور کلی، یک «تابع برازندگی» (Fitness Function) یا ، در ابتدا با استفاده از تابع هدف فرموله میشود و در عملیات ژنتیکی متوالی در نسلهای الگوریتم ژنتیک مورد استفاده قرار میگیرد.
از دیدگاه زیستشناسی، برازندگی یک «مقدار کیفی» (Qualitative Value) است که بازده تولیدِ مثل کروموزومها را میسنجد. در الگوریتم ژنتیک، از تابع برازندگی برای محاسبه شانس (یا احتمال) تولید مثل موجودیتها یا کروموزومهای موجود در جمعیت نیز استفاده میشود؛ به عبارت دیگر، به عنوان معیاری برای مشخص کردن خوب بودن کروموزومها یا جوابهای کاندید مسأله مورد استفاده قرار میگیرد (و معمولا این معیار باید بیشینه شود).
در الگوریتم ژنتیک، کروموزومها یا موجودیتهایی که بیشترین برازندگی را دارند، نسبت به دیگر کروموزومهای موجود در جمعیت، شانس بیشتری برای ترکیب و جهش (عملگرهای ژنتیکی) خواهند داشت. عملکرد صحیح برخی از عملگرهای ژنتیکی منوط به تعریف توابع برازندگی «نامنفی» (Non-Negative) است؛ با این حال، دیگر عملگرهای ژنتیکی، پیششرط نامنفی بودن تابع برازندگی را برای انجام عملیات خود تعریف نمیکنند. در مسائل بیشینهسازی، میتوان تابع برازندگی را معادل تابع هدف در گرفت. به عبارت دیگر:
در مسائل «کمینهسازی» (Minimization)، برای تولید مقادیر نامنفی در تمامی حالات و جهت منعکس کردن برازندگی نسبی رشتههای متناظر با کروموزومها یا موجودیتهای جمعیت، بسیار حیاتی است که تابع هدف اصلی مسأله به تابع برازندگی نگاشت شود. برای انجام چنین نگاشتی، روشهای متفاوتی وجود دارد. در ادامه، دو روش شایع و پرکاربرد جهت نگاشت تابع هدف به تابع برازندگی در مسائل کمینهسازی، معرفی شدهاند.
در این رابطه، تابع برازندگی و تابع هدف مسأله کمینهسازی تعریف شده است. این تبدیل، مکان جواب کمینه در فضای جوابهای مسأله را تغییر نمیدهد ولی یک مسأله کمینهسازی را به یک مسأله بیشینهسازی معادل آن تبدیل میکند. تابع جایگزین دیگری که جهت تبدیل تابع هدف به مقدار برازندگی کروموزوم ، یا ، مورد استفاده قرار میگیرد، به شکل زیر تعریف میشود.
در این رابطه، مقدار تابع هدف موجودیت یا کروموزوم اُم، اندازه جمعیت و یک مقدار بزرگ است که نامنفی شدن مقادیر برازندگی را تضمین میکند. مقدار در این تبدیل، معمولا برابر مقدار بیشینه عبارت در نظر گرفته میشود؛ در چنین حالتی، مقدار برازندگی متناظر با مقدار بیشینه تابع هدف، برابر با صفر میشود. این تبدیل نیز مکان جواب کمینه را در فضای جوابهای مسأله تغییر نمیدهد ولی یک مسأله کمینهسازی را به یک مسأله بیشینهسازی معادل آن تبدیل میکند. به مقدار تابع برازندگی یک رشته، «برازندگی رشته» (String Fitness) نیز گفته میشود.

عملگرهای الگوریتم ژنتیک
عملیات بهینهسازی در الگوریتم ژنتیک، با یک تولید جمعیت اولیه از «رشتههای تصادفی» (Random Strings) آغاز میشود (این رشتهها معادل کروموزومها یا موجودیتها یا جوابهای کاندید مسأله هستند). رشتههای تصادفی، طراحی مسأله یا به عبارت دیگر، «متغیرهای تصمیم» (Decision Variables) مرتبط با یک مسأله را نمایش میدهند.

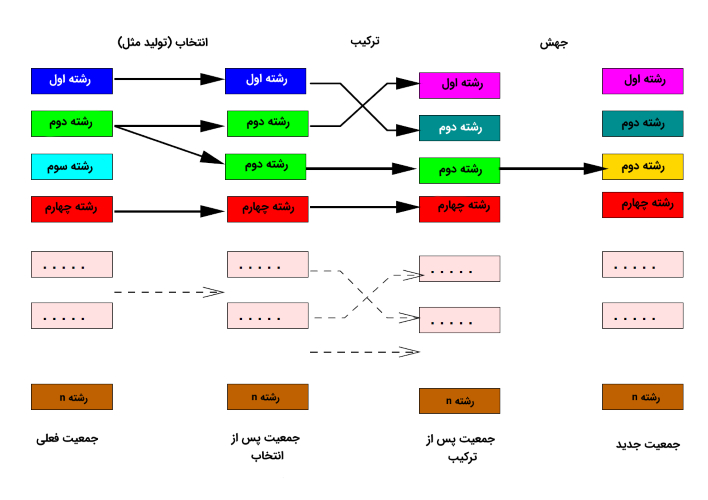
سپس، جمعیت اولیه تحت تأثیر سه دسته عملگر اصلی در الگوریتم ژنتیک قرار میگیرند تا جمعیت جدیدی از نقاط در فضای جواب مسأله تولید شود؛ جمعیت جدید، متشکل از کروموزومها یا موجودیتها یا جوابهای جدید خواهد بود. عملگرهای اصلی الگوریتم ژنتیک عبارتند از: عملگر تولید مثل، عملگر ترکیب یا آمیزش و عملگر جهش.
همانطور که پیش از این نیز اشاره شد، الگوریتم ژنتیک را میتوان به عنوان مکانیزمی جهت بیشینهسازی تابع هدف در نظر گرفت. این کار، از طریق از طریق ارزیابی کروموزومها یا بردارهای جواب انجام میشود. هدف عملگرهای اصلی در الگوریتم ژنتیک، انتخاب، ترکیب و تغییر بردارهای متناظر با جوابهایی است که در نسل کنونی، بهترین جواب برای مسأله بهینهسازی محسوب میشوند. از این طریق، جمعیت جدیدی از کروموزومها یا بردارهای جواب تولید خواهد شد.
جمعیت جدید تولید شده نیز مورد ارزیابی بیشتر قرار میگیرد و اینکار تا «خاتمه یافتن» (Termination) فرایندهای عملیاتی در الگوریتم ژنتیک ادامه پیدا میکند. تا زمانی که شرط توقف الگوریتم ژنتیک ارضا نشود، جمعیت کروموزومها یا بردارهای جواب، به وسیله عملگرهای تولید مثل، ترکیب و جهش دستکاری و ارزیابی میشوند. این رویه تا زمانی که معیار توقف الگوریتم ژنتیک ارضا شود، ادامه پیدا میکند.
یک چرخه (حلقه تکرار) از فرایند دستکاری جمعیت متشکل از کروموزومها یا بردارهای جواب، توسط عملگرهای تولید مثل، ترکیب و جهش و ارزیابی متعاقب آنها، به عنوان یک «نسل» (Generation) از الگوریتم ژنتیک شناخته میشود. در ادامه، هر یک از عملگرهای بالا به تفصیل شرح داده خواهند شد.
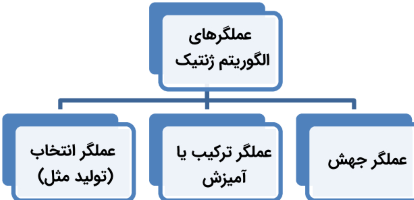
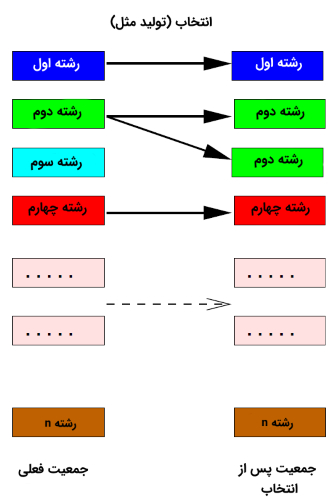
عملگر تولید مثل
عملگر تولید مثل یا «انتخاب» (Selection)، عملگری است که بهترین «رشتهها» (Strings) در یک جمعیت جدید را کپی میکند (منظور، بهترین کروموزومها یا بردارهای جواب کاندید در یک نسل است). عملگر تولیدِ مثل، معمولا اولین عملگری است که برای دستکاری جمعیت مورد استفاده قرار میگیرد و روی کروموزومها اعمال میشود. این عملگر، رشتهها یا کروموزومهای خوب جمعیت را انتخاب میکند و آنها را در مخزنی که در اصطلاح به آن Mating Pool گفته میشود، قرار میدهد؛ به همین دلیل است که به عملگر تولید مثل، عملگر انتخاب نیز گفته میشود.
بنابراین، عملیات تولید مثل در انتخاب طبیعی سبب میشود تا رشتهها یا کروموزومهایی که برازندگی بهتری نسبت به دیگر کروموزومها دارند، با تناوب بیشتری خود را تکثیر کنند. تولید مثل رشتهها یا کروموزومهای موجود در جمعیت فعلی، برای کمک به تولید جمعیت جدید در الگوریتم ژنتیک ضروری است. برای اینکه جمعیت جدید تولید شده در نسلهای آینده، برازندگی بهتری نسبت به جمعیت نسل فعلی داشته باشند، لازم است تا تناوب تولیدِ مثل در برازندهترین کروموزومهای موجود در جمعیت نسل فعلی بیشتر شود.
تاکنون، عملگرهای تولید مثل مختلفی برای الگوریتم ژنتیک توسعه داده شده است، ولی مکانیزمهای عملیاتی آنها تقریبا یکسان است؛ رشتهها یا کروموزومهای خوب از جمعیت فعلی انتخاب و کپیهای تولید شده از آنها، به شیوهای احتمالی، در مخزن Mating Pool قرار داده میشوند. نکته مهم در مورد عملیات انجام شده توسط عملگر تولید مثل یا ترکیب این است که در این مرحله، رشتهها یا کروموزومهای جدیدی (با مقادیر متغیر متفاوت از جمعیت اصلی) تشکیل نمیشود.
عملگر انتخاب مبتنی بر چرخ رولت
یکی از عملگرهای شایع و پرکاربرد برای تولید مثل در الگوریتم ژنتیک، روش «انتخاب چرخ رولت» (Roulette-Wheel Selection) نام دارد. در این عملگر، احتمال انتخاب یک رشته یا کروموزوم برای قرار گرفتن در مخزن Mating Pool، متناسب با برازندگی آن رشته یا کروموزم محاسبه میشود. بنابراین، احتمال قرار گرفتن رشته اُم در مخزن Mating Pool، متناسب یا برازندگی آن یا خواهد بود.
از آنجایی در الگوریتم ژنتیک اندازه جمعیت ثابت است، حاصل جمع تمامی احتمالات محاسبه شده برای انتخاب و قرار گرفتن کروموزومها یا رشتهها در مخزن Mating Pool، برابر با 1 خواهد بود. بنابراین، احتمال انتخاب و قرار گرفتن رشته اُم در مخزن Mating Pool، برابر است با:
در این رابطه، برابر با اندازه جمعیت است. یک روش ساده برای پیادهسازی این عملگر، تصور کردن یک چرخ رولت است که محیط آن، متناسب با برازندگی هر یک از رشتهها یا کروموزومها نشانهگذاری شده است. چرخ رولت، بار خواهد چرخید. در هر بار چرخش این چرخ، هر نمونهای که توسط نشانهگر چرخ نشان داده شود، برای قرار گرفتن در مخزن Mating Pool انتخاب میشود.
از آنجایی که محیط چرخ رولت، متناسب با برازندگی هر یک از رشتهها یا کروموزومها نشانهگذاری شده است، انتظار میرود که کپی از رشته اُم توسط این عملگر، در مخزن Mating Pool تولید شود. برازندگی میانگین جمعیت کروموزومها نیز به شکل زیر محاسبه میشود.
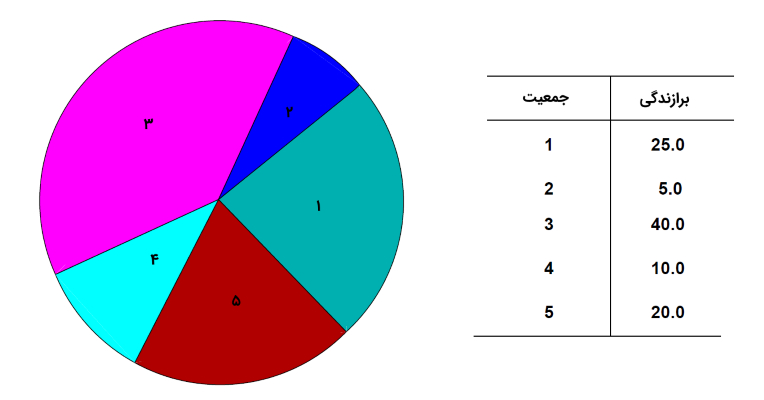
به عبارت دیگر، احتمال انتخاب هر کدام از کروموزومهای جمعیت نسل فعلی برابر با مقدار زیر خواهد بود:
شکل بالا، عملگر انتخاب چرخ رولت را برای هر کدام از موجودیت یا کروموزومهای موجود در جمعیت را نمایش میدهد. همانطور که مشاهده میشود، برازندگی کروموزومها متفاوت از یکدیگر است. از آنجایی که موجودیت یا کروموزوم سوم، مقدار برازندگی بالاتری نسبت دیگر کروموزومهای موجود در جمعیت دارد، میتوان انتظار داشت که عملگر انتخاب (تولید مثل) مبتنی بر چرخ رولت، این کروموزومها را بیش از دیگر کروموزومها انتخاب کند و در مخزن Mating Pool قرار دهد. جدول زیر، برازندگی هر کدام از کروموزومهای شکل بالا، احتمال انتخاب و احتمال تجمعی آنها را نمایش میدهد:
| جمعیت | برازندگی | احتمال انتخاب | احتمال تجمعی |
| 1 | 25 | 0٫25 | 0٫25 |
| 2 | 5 | 0٫05 | 0٫30 |
| 3 | 40 | 0٫40 | 0٫70 |
| 4 | 10 | 0٫10 | 0٫80 |
| 5 | 20 | 0٫20 | 1 |
به عنوان نمونه، به مثال جمعیت بالا توجه کنید. برای انتخاب موجودیت یا کروموزوم از بین جمعیت نسل فعلی، تعداد عدد تصادفی بین صفر و یک تولید خواهد شد. سپس، به ازاء هر کدام از مقادیر تصادفی تولید شده، شرطهای زیر به ترتیب چک میشوند:
- در صورتی که مقدار تصادفی تولید شده کوچکتر از احتمال تجمعی کروموزوم اول (0٫25) باشد، کروموزوم 1 انتخاب میشود. در غیر این صورت، شرط بعدی چک میشود.
- در صورتی که مقدار تصادفی تولید شده کوچکتر از احتمال تجمعی کروموزوم دوم (0٫30) باشد، کروموزوم 2 انتخاب میشود. در غیر این صورت، شرط بعدی چک میشود
- در صورتی که مقدار تصادفی تولید شده کوچکتر از احتمال تجمعی کروموزوم سوم (0٫70) باشد، کروموزوم 3 انتخاب میشود. در غیر این صورت، شرط بعدی چک میشود.
- در صورتی که مقدار تصادفی تولید شده کوچکتر از احتمال تجمعی کروموزوم چهارم (0٫80) باشد، کروموزوم 4 انتخاب میشود. در غیر این صورت، شرط بعدی چک میشود.
- در نهایت، در صورتی هیچ یک از شرطهای بالا صحیح نباشند، کروموزوم 5 انتخاب میشود.
عملگر انتخاب باقی مانده تصادفی (بدون جایگذاری)
این عملگر، روش بهتری برای انتخاب رشتهها یا کروموزومها است. ایده اصلی این روش این است که رشتهها یا کروموزومها، بر اساس تعداد دفعات تولید مثل از آنها، از جمعیت جدید حذف و یا در جمعیت جدید تکثیر میشوند. برای چنین کاری، پارامتر تعداد «دفعات تولید مثل» (Reproduction Count) به ازاء هر کدام از رشتهها یا کروموزومها محاسبه میشود.
پارامتر تعداد دفعات تولید مثل متناظر با هر یک از رشتهها یا کروموزومها، بر اساس مقدار برازندگی (هر کدام از رشتهها) و بدون جایگذاری محاسبه خواهد شد. این روش، نسبت به دیگر عملگرهای انتخاب برتر است و برای استفاده در الگوریتم ژنتیک پیشنهاد میشود. در این عملگر، ابتدا احتمال انتخاب یا به شکل زیر محاسبه میشود:
بنابراین، تعداد دفعات تولید مثل مورد انتظار به ازاء هر رشته یا کروموزوم، از طریق رابطه زیر محاسبه میشود:
در این رابطه، برابر با اندازه جمعیت است. از قسمت کسری مقادیر تولید شده به ازاء هر رشته یا کروموزوم، به عنوان احتمالات انتخاب آن کروموزومها استفاده میشود. به عنوان نمونه، در صورتی که پارامتر تعداد دفعات تولید مثل مورد انتظار یک رشته یا کروموزوم، برابر با باشد، حتما یک کپی از این رشته در جمعیت جدید وجود خواهد داشت. همچنین، یک کپی دیگر با احتمال 0٫50، برای قرار گرفتن در جمعیت جدید انتخاب خواهد شد.
این کار تا زمانی انجام میشود که پارامتر تعداد دفعات تولید مثل مورد انتظار، به ازاء هر کدام از کروموزمها یا رشتههای موجود در جمعیت محاسبه شود. کروموزومهایی که پارامتر تعداد دفعات تولید مثل مورد انتظار آنها برابر با صفر باشد، از جمعیت کروموزومها حذف خواهند شد.
کروموزومهایی که پارامتر دفعات تولید مثل مورد انتظار آنها برابر با مقداری غیر صفر باشد، تعداد کپیهای تکثیر شده از کروموزوم آنها در جمعیت جدید، متناسب با مقدار پارامتر تعداد دفعات تولید مثل مورد انتظار، محاسبه شده خواهد بود.
همچنین، اندازه جمعیت جدید (حاصل شده پس از فرایند تولید مثل) ثابت و با اندازه جمعیت قبلی (پیش از عملیات تولید مثل) برابر خواهد بود. با چنین کاری، عملیات تولید مثل در الگوریتم ژنتیک کامل خواهد شد.
تقریبا تمامی عملگرهای انتخاب یا تولید مثل، اصول کاری مشابه یکدیگر دارند و فقط تعداد کپیهایی که به هر کروموزوم یا رشته اختصاص میدهند متفاوت خواهد بود. در نهایت، این نکته شایان توجه است که در تمامی عملگرهای تولید مثل یا انتخاب برای الگوریتم ژنتیک، رشتههایی به تعداد بیشتر در جمعیت جدید کپی میشوند که برازندگی آنها، از دیگر رشتههای موجود در جمعیت بیشتر باشند.
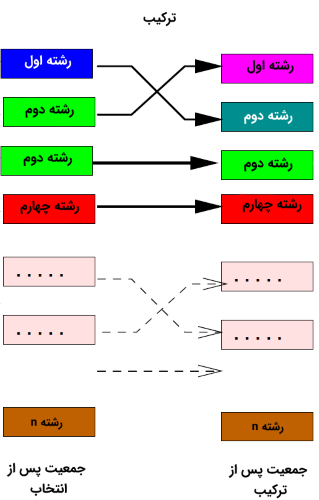
عملگر ترکیب یا آمیزش
از عملگر «ترکیب یا آمیزش» (Crossover)، برای «بازترکیب» (Recombine) دو رشته یا کروموزوم استفاده میشود. این کار، با هدف تولید رشتهها یا کروموزومهای بهتر انجام میشود. در عملیات ترکیب در الگوریتم ژنتیک، طریق ترکیب کردن مواد ژنتیکی دو کروموزوم موجود در جمعیت نسل قبل، کروموزومهای جدیدی در نسلهای فعلی میشود. به عبارت دیگر، فرایند بازترکیب، ژنهای موجود در دو کروموزوم را ترکیب و از این طریق، کروموزومهای جدیدی در جمعیت فعلی تولید میکند.
چنین فرایندی به صورت تکراری و در تمامی نسلهای یک الگوریتم ژنتیک انجام خواهد شد. در فرایند تولید مثل، معمولا تعداد کپیهای ایجاد شده از کروموزومهایی که برازندگی بالایی دارند، بیشتر از دیگر کروموزمها خواهد بود. در پایان فرایند تولید مثل، مخزن Mating Pool تشکیل میشود (و تمامی کپیهای تولید شده در آن قرار میگیرد).
همانطور که پیش از این نیز اشاره شد، در مرحله تولید مثل، رشتهها یا کروموزومهای جدیدی (با مقادیر متغیر متفاوت از جمعیت اصلی) در جمعیت تشکیل نمیشوند. در این مرحله (و پس از عملیات حاصل از عملگر ترکیب)، رشتهها یا کروموزومهای جدیدی از طریق تبادل اطلاعات (ژنی) میان رشتهها یا کروموزومهای موجود در مخزن Mating Pool تشکیل میشوند.
به دو کروموزوم یا رشتهای که در عملیات ترکیب یا آمیزش مشارکت میکنند، کروموزومهای «والد» (Parents) گفته میشود. همچنین، کروموزومهایی که در اثر فرایند ترکیب یا آمیزش تولید میشوند، کروموزومهای «فرزند» (Children) نامیده میشوند.
بنابراین، یک نتیجهگیری ممکن از عملیات ترکیب میتواند این گونه باشد که ترکیب زیررشتههای خوب (منظور، مجموعهای از ژنهای خوب در کروموزومهای والد) از رشتهها یا کروموزومهای والدین با یکدیگر، میتواند منجر به تولید رشتهها یا کروموزومهای فرزند خوب شوند. چنین برداشتی، زمانی منطقی و صحیح به شمار میآید که عملیات ترکیب زیررشتهها، به صورت مشخص و روی ژنهایی از رشتههای والدین صورت بگیرد که ترکیب آنها، سبب تولید رشته یا کروموزوم فرزند خوب میشود (ترکیب این زیر رشتهها، به صورت احتمالی انجام میشود).
در صورتی که عملیات انتخاب زیررشتهها و ترکیب آنها، بر اساس فرایندهای تصادفی انجام شود، هیچ تضمینی وجود ندارد که فرزندهای حاصل، زیررشتههای خوب والدین خود را به ارث ببرند. در این حالت، خوب بودن یا خوب نبودن فرزندان، به طور مستقیم، به ژنهایی در رشتههای والدین بستگی دارد که در عملیات ترکیب و تولید فرزندان مشارکت دارند.
با این حال، چنین منطقی در الگوریتم ژنتیک نگران کننده نیست؛ زیرا در صورتی که کروموزومهای فرزند خوبی توسط عملیات ترکیب یا آمیزش تولید شوند، در نسلهای بعدی، با احتمال بیشتری انتخاب میشوند و کپیهای بیشتری از آنها تولید میشود. کپیهای تولید شده نیز در مخزن Mating Pool قرار میگیرند تا در مراحل بعدی مورد دستکاری ژنی قرار بگیرند.
با این حال، طبیعت تصادفی عملگرهای ژنتیک (نظیر عملگر ترکیب) ممکن است اثر «مخرب» (Detrimental) یا «سودمند» (Beneficial) در کیفیت کروموزومها یا همان جوابهای مسأله داشته باشد. در صورتی که کروموزومهای فرزند خوبی در نتیجه ترکیب تولید شوند، در جمعیت نسلهای بعدی، کروموزومهای خوبی مشارکت خواهند کرد و برعکس.
بنابراین، برای حفظ برخی از رشتهها یا کروموزومهای خوبی که در مخزن Mating Pool وجود دارند، تمامی رشتهها یا کروموزومهای موجود در مخزن Mating Pool، توسط عملگر ترکیب دستکاری نخواهند شد. برای چنین کاری، از مفهومی به نام «احتمال ترکیب» (Crossover Probability) یا استفاده میشود.
وقتی که در الگوریتم ژنتیک، پارامتر احتمال ترکیب تعریف میشود، یعنی تنها درصد از رشتهها یا کروموزومهای موجود در جمعیت، توسط عملگر ترکیب دستکاری میشوند. به عبارت دیگر، درصد از رشتهها یا کروموزومهای موجود در جمعیت، به همان شکل اصلی خودشان در جمعیت نسل فعلی باقی خواهند ماند.
در الگوریتم ژنتیک، از عملگر ترکیب برای جستجوی رشتهها یا کروموزومهای جدید در فضای جواب (فضای جستجو) استفاده میشود. البته، عملگر جهش در الگوریتم ژنتیک نیز برای چنین کاربردی مورد استفاده قرار میگیرد.
تاکنون، عملگرهای ترکیب متعددی برای الگوریتم ژنتیک توسعه داده شدهاند. روشهای «تک نقطهای» (Single Point) و «دو نقطهای» (Two point)، از جمله مهمترین عملگرهای ترکیب در الگوریتم ژنتیک محسوب میشوند. در غالب عملگرهای ترکیب توسعه داده شده برای الگوریتم ژنتیک، دو رشته یا کروموزوم به طور تصادفی از مخزن Mating Pool انتخاب میشوند و بخشهایی از رشتههای این دو کروموزوم با یکدیگر ترکیب میشوند تا رشتهها یا کروموزومهای جدیدی پدید آیند.
عملیات ترکیب در سطح رشته انجام میشود و پس از انتخاب دو رشته یا کروموزوم والد، ژنهای آنها با یکدیگر مبادله میشوند تا کروموزومهای فرزند جدید شکل بگیرد. در عملگر ترکیب تک نقطهای، یک ژن به شکل تصادفی، در امتداد یکی از دو رشته یا کروموزوم والد، به عنوان «محل ترکیب» (Crossover Site) در عملیات ترکیب انتخاب میشود. سپس، تمامی ژنهای موجود در سمت راست محل ترکیب رشته اول، با ژنهای متناظر آنها در کروموزوم یا رشته دوم جا به جا میشوند. چگونگی انجام عمل ترکیب تک نقطهای روی کروموزومهای والد (توسط عملگر متناظر آن در الگوریتم ژنتیک)، در شکل زیر نمایش داده شده است.
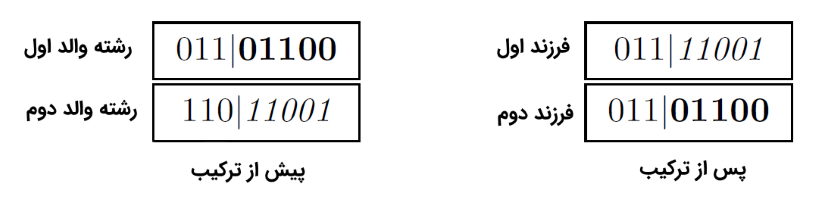
همانطور که در شکل بالا مشهود است، در عملگر ترکیب تک نقطهای، یک محل ترکیب به شکل تصادفی انتخاب میشود (در شکل بالا، محل ترکیب به شکل یک خط عمودی نمایش داده شده است). تمامی ژنهایی که در سمت راست محل ترکیب انتخاب شده (در دو رشته یا کروموزوم) قرار دارند، با یکدیگر مبادله خواهند شد و از این طریق، دو کروموزوم یا رشته جدید تولید میشود.
عملگر ترکیب دو نقطهای، حالت خاصی از عملگر ترکیب تک نقطهای محسوب میشود؛ با این تفاوت که به جای یک محل ترکیب، دو محل ترکیب در رشتهها یا کروموزومهای والد انتخاب میشوند و ژنهای قرار گرفته میان محلهای ترکیب انتخابی، به نحوی که در شکل 5 نمایش داده شده است، با یکدیگر مبادله میشوند.

عملگر ترکیب تک نقطهای برای حالتی مناسب است که طول رشتهها یا کروموزومها کوتاه هستند. در صورتی که طول رشتهها یا کروموزوها بلند باشند، بهتر است که از عملگر ترکیب دو نقطهای برای تولید کروموزومهای جدید استفاده شود. بنابراین، در ادامه این مطلب، از عملگر ترکیب دو نقطهای، به عنوان عملگر پیشفرض برای انجام عملیات ترکیب استفاده میشود.
هدف اصلی عملیات ترکیب در الگوریتم ژنتیک این است که با ترکیب ژنهای دو کروموزوم یا رشته والد، به کروموزومها یا رشتههای فرزندی دست پیدا شود که به احتمال زیاد، ویژگیهای بهتری نسبت به کروموزومهای والد از خود نشان میدهند (برازندگی بهتری نسبت به کروموزومهای والد دارند).
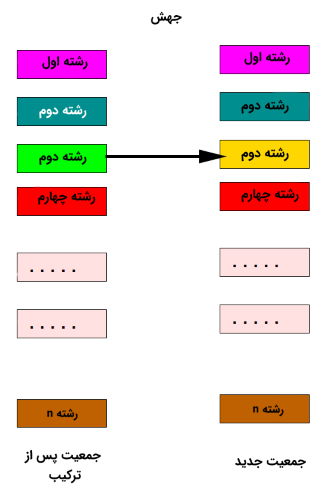
عملگر جهش
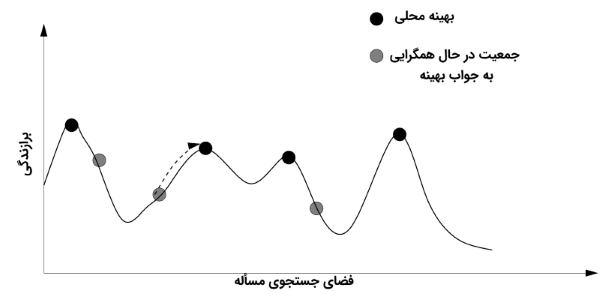
عملگر جهش یکی از مهمترین فرایندهای تکاملی برای رسیدن به جواب بهینه در الگوریتم ژنتیک محسوب میشود. در عملگر جهش، به شکل تصادفی، اطلاعات جدیدی به فرایند جستجو در الگوریتم ژنتیک اضافه میشود. چنین ویژگی مهمی به الگوریتم ژنتیک کمک میکند تا از قرار گرفتن در دام «بهینه محلی» (Local Optimum) فرار کند.
زمانی که در نسلهای متوالی، از عملیات ترکیب و تولید مثل به دفعات روی رشتهها یا کروموزومها استفاده میشود، جمعیت کروموزومها یا جوابهای کاندید به «همگن» (Homogeneous) شدن گرایش پیدا میکند. عملگر جهش به الگوریتم ژنتیک کمک میکند تا «تنوع» (Diversity) در جمعیت کروموزومها یا جوابهای کاندید افزایش پیدا کند.
عملگر جهش ممکن است منجر به تغییرات عمده در کروموزومهای فرزندان تولید شده شود و سبب شود که کروموزومها یا رشتههای فرزند تولید شده، ژنهای کاملا متفاوتی نسبت به کروموزوم یا رشته والدین داشته باشند.
به بیان سادهتر، عملگر جهش، فرایندی تصادفی برای به هم ریختن و ایجاد اختلال در اطلاعات ژنتیکی محسوب میشود. بر خلاف عملگر ترکیب، عملگر جهش در سطح ژن کار میکند؛ یعنی، زمانی که ژنها از رشته یا کروموزوم فعلی در رشته یا کروموزوم جدید کپی میشوند، این احتمال وجود دارد که هر کدام از این ژنها جهش پیدا کنند. این احتمال معمولا مقدار بسیار کوچکی است که به آن «احتمال جهش» (Mutation Probability) یا گفته میشود.
در صورتی که از نمایش بیتی (صفر و یک) برای مشخص کردن مقادیر متغیرهای مسأله یا ژنها استفاده شود، جهت انجام عملیات جهش، از مکانیزم «پرتاب سکه» (Coin Toss) در الگوریتم ژنتیک استفاده میشود؛ یعنی، در صورتی که مقدار تصادفی (بین صفر و یک) از احتمال جهش کمتر باشد، مقدار ژن یا همان بیت ژن معکوس میشود. به عبارت دیگر، مقادیر ژنی برابر با یک تبدیل به صفر و مقادیر ژنی برابر با صفر، تبدیل به یک خواهند شد.
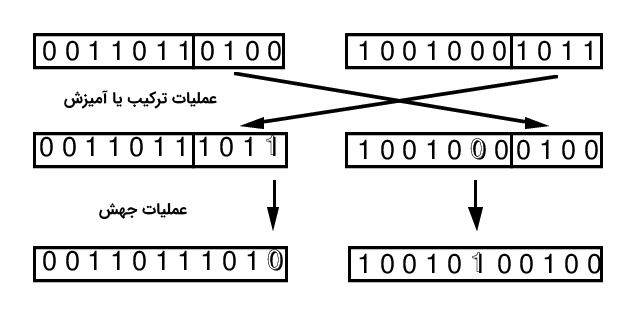
اگر به مکانیزم جهش دقت شود میتوان دریافت که عملگر جهش از طریق معکوس کردن تصادفی مقدار ژنها، باعث ایجاد تنوع در جمعیت کروموزومها یا جوابهای کاندید میشود. معکوس کردن تصادفی مقدار ژنها، هم باعث همگرایی به جواب بهینه بهتر در فضای جستجوی مسأله میشود و هم منجر به تغییرات اساسی در کدهای ژنتیکی کروموزومها میشود؛ پدیدهای که مسیر رسیدن به جواب بهینه سراسری را در نسلهای متوالی از الگوریتم ژنتیک هموارتر میکند. از طرف دیگر، عملگر جهش ممکن است منجر به تولید رشتهها یا کروموزومهای ضعیفی شود که به هیچ عنوان توسط عملگر تولید مثل یا انتخاب، انتخاب نخواهند شد.
عملگر جهش مکانیزم هوشمندانهای برای جستجوی محلی در فضای جستجوی جوابهای مسأله به شمار میآید. با استفاده از عملگر جهش در الگوریتم ژنتیک، رشتهها یا کروموزومهای جدیدی در همسایگی رشته یا کروموزوم فعلی ایجاد میشوند. در نتیجه، عملگر جهش سبب ایجاد مکانیزم جستجوی محلی اطراف کروموزومهای فعلی میشود. همچنین، عملگر جهش سبب حفظ تنوع در جمعیت کروموزومها یا جوابهای کاندید میشود. به عنوان نمونه، به جمعیت زیر توجه کنید. این جمعیت، از 4 کروموزم تشکیل شده است که هر کدام از آنها، یک رشته 8 بیتی هستند:
01101011
00111101
00010110
01111100
با دقت به جمعیت کروموزومی نمایش داده شده میتوان دریافت که اولین ژن تمامی رشتهها از سمت چپ، صفر (0) است. در صورتی که ابتداییترین ژن رشته متناظر با جواب بهینه سراسری برابر با (1) باشد، هیچ کدام از عملگرهای تولید مثل (انتخاب) و ترکیب قادر به تولید مقدار یک (1) در این مکان ( اولین ژن رشته از سمت چپ) نخواهند بود. استفاده از عملگر جهش در الگوریتم ژنتیک سبب میشود تا مقدار اولین ژن این رشتهها، با احتمال از صفر (0) به یک (1) تغییر پیدا کند.
سه عملگر معرفی شده برای انجام عملیات تولید مثل (انتخاب)، ترکیب و جهش، عملگرهای ساده و سر راستی هستند. عملگر تولید مثل، رشته خوب را انتخاب و عملگر ترکیب، بهترین زیررشتههای موجود در رشتههای خوب جمعیت را با یکدیگر ترکیب میکند؛ به امید اینکه جوابها یا رشتهها یا کروموزومهای حاصل، جوابها یا رشتهها یا کروموزومهای بهتری نسبت به والدین خود باشند. عملگر جهش، ژنهای کروموزومها را به شکل محلی تغییر میدهد و از این طریق، منجر به ایجاد جوابها یا رشتهها یا کروموزومهای بهتر میشود.
با اینکه هیچگونه تضمینی برای ایجاد جوابها یا رشتهها یا کروموزومهای خوب در نتیجه عملیات این عملگرها وجود ندارد، با این حال میتوان از دو مورد زیر تا حد زیادی مطمئن بود:
- در صورتی که جوابها یا رشتهها یا کروموزومهای بدی در نتیجه عملگرهای تولید مثل (انتخاب)، ترکیب و جهش حاصل شوند، در عملیات تولیدِ مثل (انتخاب) نسل بعد حذف خواهند شد.
- در صورتی که جوابها یا رشتهها یا کروموزومهای خوبی در نتیجه عملگرهای تولید مثل (انتخاب)، ترکیب و جهش حاصل شوند، الگوریتم ژنتیک در نسلهای متوالی، تاکید بیشتری روی آنها خواهد داشت.
استفاده از عملگرهای تولید مثل (انتخاب)، ترکیب و جهش روی رشتهها یا کروموزومهای نسل حاضر، سبب ایجاد جمعیت نسل بعد خواهد شد. از جمعیت تولید شده نیز برای تولید جمعیت نسل بعد از آن (از طریق عملگرهای تولید مثل (انتخاب)، ترکیب و جهش) استفاده میشود. این چرخه در نسلهای بعدی ادامه پیدا میکند و در هر نسل، الگوریتم ژنتیک یک قدم به تولید جواب بهینه سراسری نزدیکتر خواهد شد. مقدار برازندگی هر یک از رشتهها یا کروموزومهای جمعیت جدید نیز از طریق قرار دادن مقادیر متغیرها در تابع برازندگی و کد گشایی آنها به دست میآید.
مقادیر به دست آمده، برازندگی هر یک از رشتهها یا کروموزومهای جمعیت نسلهای جدید را نمایش خواهند داد. محاسبه برازندگی هر یک از رشتهها یا کروموزومها، پایان یک حلقه از الگوریتم ژنتیک خواهد بود که به آن «نسل» (Generation) گفته میشود. در هر نسل، در صورتی که برازندگی یک کروموزوم یا جواب بهبود پیدا کند، به عنوان یکی از جوابهای خوب شناخته خواهد شد. این کار تا زمانی که الگوریتم ژنتیک به جواب بهینه سراسری همگرا شود ادامه پیدا میکند.
نمایش عملکرد الگوریتم ژنتیک در بهینهسازی توابع
برای اینکه با عملکرد الگوریتم ژنتیک در همگرایی به جواب بهینه بهتر آشنا شویم، یک تابع دو متغیری ساده با استفاده از الگوریتم ژنتیک حل خواهد شد. گامهای تفصیلی و جوابهای حاصل شده در ادامه نمایش داده شدهاند. مسأله کمینهسازی زیر را در بازه در نظر بگیرید:
جواب بهینه سراسری برای مسأله بهینهسازی فوق در نقطه حاصل میشود. در این نقطه، مقدار تابع هدف نمایش داده شده برابر با صفر خواهد بود.
مرحله اول
برای حل این مسأله توسط الگوریتم ژنتیک، از کدبندی باینری برای نمایش متغیرهای و استفاده میشود. در این مسأله، از 10 بیت برای نمایش هر متغیر استفاده شده است؛ در نتیجه، از آنجایی که مسأله دو متغیری است، طول رشته یا کروموزوم برابر با 20 خواهد بود.
با انتخاب ده بیت برای نمایش متغیرهای مسأله، الگوریتم ژنتیک به دقتی برابر با یا ۰٫۰۰۶ در بازه (6 ، 0) دست خواهد یافت. احتمال ترکیب () و احتمال جهش () به ترتیب برابر با 0٫۸ و ۰٫05 در نظر گرفته شده است.
اندازه جمعیت برابر با 20 و تعداد نسلها نیز برابر با 30 خواهد بود. از یک مولد تصادفی تعبیه شده برای تولید مقادیر تصادفی و از یک «نمونهگیری تصادفی بدون جایگذاری» (Stochastic Sampling Without Replacement) به عنوان عملگر انتخاب یا تولید مثل استفاده میشود. در مرحله بعد، برازندگی تمامی رشتهها یا کروموزومهای موجود در جمعیت سنجیده میشود. در این مثال کاربردی، تنها برازندگی رشته یا کروموزوم اول محاسبه میشود.
مرحله دوم
در این مرحله، برازندگی تمامی رشتهها یا کروموزومهای موجود در جمعیت سنجیده میشود. این کار از طریق کد گشایی رشتهها یا کروموزومها انجام میشود. زیر رشته اول (1000001110) با استفاده از تابع زیر به مقداری برابر با یا 525 کد گشایی میشود.
بنابراین، با استفاده از تابع زیر، مقدار پارامتر متناظر، برابر با یا 3٫۰۹ خواهد بود.
همچنین، فرض کنید که زیر رشته دوم (0001110000) به مقداری برابر با 12 کد گشایی میشود. مقدار پارامتر متناظر با این زیر رشته، یا 0٫۶۶ خواهد شد. بنابراین اولین زیر رشته، برابر با نقطه در فضای جستجوی مسأله خواهد بود. با جایگذاری این مقادیر در تابع هدف، مقدار تابع هدف برابر با ۱۲٫۸۱۶ برای رشته اول در نقطه تولید خواهد شد.
با توجه به اینکه مسأله بهینهسازی تعریف شده در اصل یک مسأله کمینهسازی است، مقدار برازندگی رشته اول به شکل محاسبه میشود. از مقدار برازندگی محاسبه شده، در عملیات تولید مثل (عملگر انتخاب یا تولید مثل) استفاده میشود. جدول زیر، جزئیات مرتبط با رشتهها یا کروموزومهای دوم تا دهم جمعیت را نشان میدهد.
جزئیات مربوط به رشتههای دوم (شماره 1) تا دهم (شماره 9) تا مرحله انتخاب یا تولید مثل کروموزومها
| شماره | زیر رشته اول | زیر رشته دوم | پارامتر اول | پارامتر دوم | مقدار تابع هدف | مقدار تابع برازندگی | تعداد کپیها در نسل بعد |
| 1 | 1100110000 | 0101111110 | 4.7 | 2.2 | 207.9 | 0.005 | 1 |
| 2 | 0010110110 | 0000110000 | 1.0 | 0.2 | 126.0 | 0.008 | 1 |
| 3 | 0100001001 | 1000011011 | 1.5 | 3.1 | 50.0 | 0.020 | 2 |
| 4 | 1011001101 | 0100111010 | 4.2 | 1.8 | 73.0 | 0.014 | 1 |
| 5 | 1001111001 | 0111100011 | 3.7 | 2.8 | 53.9 | 0.018 | 1 |
| 6 | 1000111011 | 1101111111 | 3.3 | 5.2 | 601.2 | 0.002 | 0 |
| 7 | 0011100111 | 1001110100 | 1.3 | 3.6 | 92.7 | 0.011 | 1 |
| 8 | 0110001101 | 1011111111 | 2.3 | 4.5 | 243.4 | 0.004 | 1 |
| 9 | 0010101011 | 1000110000 | 1.0 | 3.2 | 67.9 | 0.014 | 1 |
مرحله سوم
از آنجایی که الگوریتم ژنتیک هنوز به حد بالای تعداد نسلهای لازم برای همگرایی به جواب بهینه نرسیده است، کنترل اجرای الگوریتم به مرحله بعد داده میشود.
مرحله چهارم
در این مرحله، عملیات انتخاب یا تولید مثل با استفاده از نمونهگیری تصادفی بدون جایگذاری انجام میشود. به عبارت دیگر، تعداد کپیهای هر رشته یا کروموزم در مخزن Mating Pool، بر اساس برازندگی آنها مشخص میشود. به عنوان نمونه، رشته یا کروموزم هفتم (شماره 6) تعداد 0 کپی، رشته یا کروموزم دوم تعداد 1 کپی و رشته یا کروموزم چهارم تعداد 2 کپی به آنها در مخزن Mating Pool اختصاص داده خواهد شد.
دقت کنید از آنجایی که مقدار تابع هدف رشته یا کروموزوم هفتم (شماره 6) بسیار بالاتر از دیگر رشتهها است، تعداد 0 کپی به آن در مخزن Mating Pool اختصاص داده شده است؛ ولی رشته یا کروموزوم چهارم، تعداد 2 کپی به آن در مخزن Mating Pool اختصاص داده خواهد شد. به عبارت دیگر، دو کپی از این رشته یا کروموزوم در جمعیت نسل بعد حضور خواهد داشت. با این کار فرایند تولید مثل یا انتخاب به اتمام میرسد.
در ادامه، از عملگرهای ترکیب و جهش برای دستکاری ژنی کروموزومهای والدین و تولید کروموزومهای فرزند استفاده میشود. دقت داشته باشید پیش از اینکه عملگرهای جهش و ترکیب روی کروموزومها اعمال شوند، کروموزومهایی که مقدار تابع هدف آنها بالا است از جمعیت حذف میشوند. با این حال، پس از انجام عملیات جهش و ترکیب روی کروموزومهای انتخاب شده، برازندگی برخی از کروموزومها بدتر (نظیر کروموزوم شماره 8) و برازندگی برخی دیگر از آنها بهتر میشوند (نظیر کروموزوم شماره 1).
جزئیات مرتبط با رشتهها یا کروموزومهای اول تا دهم جمعیت، پس از انجام عملیات جهش و ترکیب روی آنها در جدول زیر نمایش داده شده است.
جزئیات مربوط به رشتههای دوم (شماره 1) تا دهم (شماره 9) پس از عملیات ترکیب و جهش روی جمعیت
| شماره | زیر رشته اول | زیر رشته دوم | پارامتر اول | پارامتر دوم | مقدار تابع هدف | مقدار تابع برازندگی |
| 1 | 011010000 | 00001111110 | 2.4 | 0.7 | 34.6 | 0.028 |
| 2 | 001011011 | 11001110000 | 0.5 | 1.0 | 122.5 | 0.008 |
| 3 | 010000100 | 10000011001 | 1.0 | 3.6 | 94.0 | 0.011 |
| 4 | 101000111 | 11010111110 | 1.5 | 0.1 | 100.6 | 0.010 |
| 5 | 100111101 | 10111100011 | 3.8 | 4.1 | 252.2 | 0.004 |
| 6 | 001110101 | 11001000011 | 3.7 | 2.8 | 55.0 | 0.018 |
| 7 | 11001000011 | 00010110100 | 1.3 | 3.4 | 67.4 | 0.015 |
| 8 | 111000110 | 10110111101 | 5.3 | 2.6 | 427.7 | 0.002 |
| 9 | 001110111 | 00101010000 | 1.4 | 1.9 | 53.0 | 0.018 |
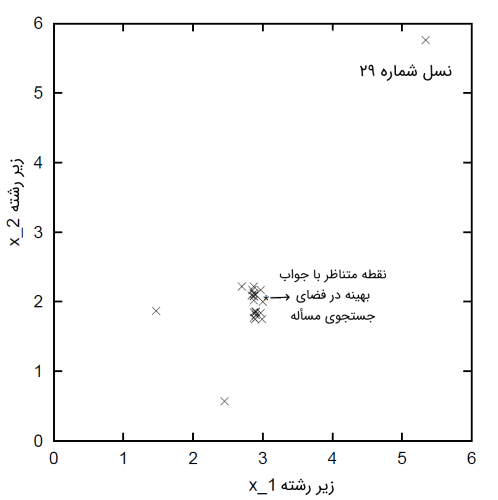
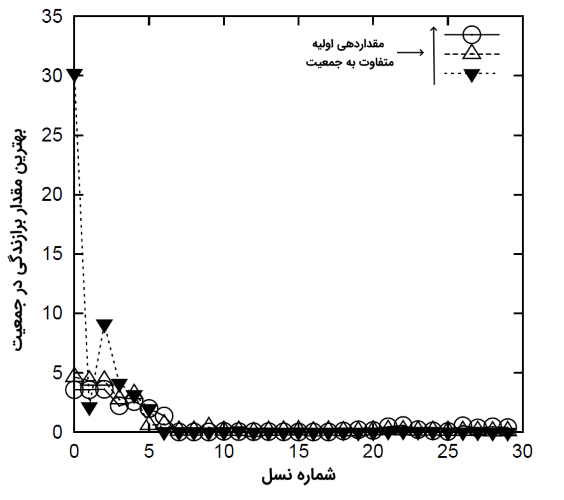
پیشرفتهای حاصل شده پس از نسل اول معنادار نخواهد بود. با این حال، با مقایسه جوابهای به دست آمده پس از نسل اول و جوابهای به دست آمده پس از نسل سیاُم، به راحتی میتوان نتیجه گرفت که پیشرفتهای بسیار خوبی در زمینه همگرایی به جواب بهینه حاصل شده است.

تفاوت الگوریتم ژنتیک و الگوریتمهای بهینهسازی و جستجوی سنتی
الگوریتم ژنتیک، تفاوتهای بنیادی با الگوریتمهای جستجو و بهینهسازی سنتی دارد. مهمترین این تفاوتها عبارتند از:
- الگوریتم ژنتیک از طریق کدبندی مجموعه جوابهای کاندید، توابع را بهینه و مسائل بهینهسازی را حل میکند. در حالی که الگوریتمهای بهینهسازی و جستجوی سنتی، از مجموعه جوابهای کاندید برای بهینهسازی استفاده میکنند.
- الگوریتم ژنتیک، مجموعهای از جوابهای کاندید را برای یافتن جواب بهینه جستجو میکند. در حالی که الگوریتمهای بهینهسازی و جستجوی سنتی، از همان ابتدا به دنبال یک جواب واحد هستند.
- الگوریتم ژنتیک، از اطلاعات مرتبط با تابع برازندگی برای حل مسائل بهینهسازی بهره میبرد. در حالی که الگوریتمهای بهینهسازی و جستجوی سنتی، از مشتق تابع هدف و دیگر اطلاعات کمکی استفاده میکنند.
- الگوریتم ژنتیک از قوانین گذار «احتمالی» (Probabilistic) برای بهینهسازی و جستجو استفاده میکنند. در حالی که الگوریتمهای بهینهسازی و جستجوی سنتی، از قوانین «قطعی» (Deterministic) بهره میگیرند.
کاربردهای الگوریتم ژنتیک
در صورتی که بتوانید جوابهای کاندید یک مسأله را در قالب کروموزومها کدبندی کنید، به راحتی خواهید توانست از الگوریتم ژنتیک برای حل مسأله و مقایسه عملکرد (برازندگی) نسبی جوابهای بهینه حاصل شده استفاده کنید. نمایش دقیق و مؤثر از متغیرهای مسأله و پیادهسازی ساز و کارهای با معنی برای ارزیابی برازندگی جوابهای کاندید، مهمترین عوامل در موفقیت در کاربردهای تولید شده از الگوریتم ژنتیک است.
نقطه قوت الگوریتم ژنتیک، در سادگی و ظرافت آنها به عنوان یک الگوریتم جستجوی قدرتمند و قدرت آنها در کشف سریع جوابهای خوب برای مسائل سخت و «با ابعاد بالا» (High Dimensional) نهفته است. الگوریتم ژنتیک زمانی میتوانند مفید و مؤثر واقع شود که:
- فضای جستجوی مسأله بزرگ، پیچیده و دارای ساختار بندی ضعیف باشد.
- دانش دامنه نایاب باشد و یا دانش خبره، جهت محدود کردن فضای جستجو، به سختی کدبندی شود.
- هیچگونه تحلیل ریاضی در دسترس نباشد.
- روشهای جستجوی سنتی با شکست مواجه شوند.
از الگوریتمهای ژنتیک، جهت حل مسأله و مدلسازی استفاده میشود. امروزه، از الگوریتمهای ژنتیک و مشتقات آن، در دامنه وسیعی از مسائل علمی و مهندسی استفاده میشود. مهمترین کاربردهای الگوریتم ژنتیک عبارتند از:
- بهینهسازی: دامنه وسیعی از مسائل بهینهسازی نظیر «بهینهسازی عددی» (Numerical Optimization) و «بهینهسازی ترکیبیاتی» (Combinatorial Optimization).
- «برنامهنویسی خودکار» (Automatic Programming): برنامهنویسی سیستمهای کامپیوتری برای انجام وظایف خاص و طراحی ساختارهای محاسباتی نظیر «اتوماتای سلولی» (Cellular Automata) و «شبکههای مرتبسازی» (Sorting Networks).
- «یادگیری ماشین» (Machine Learning): «دستهبندی» (Classification)، «پیشبینی» (Prediction)، طراحی «شبکههای عصبی مصنوعی» (Artificial Neural Networks) و سایر موارد.
- مدلهای «سیستم ایمنی» (Immune Systems): برای مدلسازی جنبههای مختلف سیستم ایمنی طبیعی، از جمله برخی جهشها در طول دوره حیات موجودات و اکتشاف خانوادههای «چندژنی» (Multi-Genes) در طول فرایند تکامل.
- مدلهای اقتصادی: مدلسازی فرایند نوآوری، توسعه استراتژیهای مناقصه و ظهور بازارهای اقتصادی.

کدهای پیادهسازی الگوریتم ژنتیک در زبانهای برنامهنویسی مختلف
در این بخش، کدهای پیادهسازی الگوریتم ژنتیک برای مدلسازی و حل «الگوریتم راسو» (Weasel algorithm) [+] نمایش داده شده است. هدف این الگوریتم این است که نشان دهد تغییرات تصادفی در ژنها و ترکیب آنها با یک مکانیزم انتخاب غیر تصادفی، منجر به تولید نتایجی متفاوت و بهتر از شانس خالص در فرایندهای تکاملی خواهد شد. مشخصات این مسأله به شکل زیر است:
- جمعیت اولیه: یک آرایه 28 عنصری متشکل از الفبای ABCDEFGHIJKLMNOPQRSTUVWXYZ.
- هدف نهایی: تبدیل رشته ورودی یا جمعیت اولیه به رشته METHINKS IT IS LIKE A WEASEL.
- تابع برازندگی: تابعی که شباهت آرگومان ورودی را به رشته نهایی یا هدف نهایی مشخص میکند.
- عملگرهای تکاملی (پیادهسازی عملگر انتخاب و جهش ضروری است، ولی پیادهسازی عملگر ترکیب اختیاری است)
پیادهسازی الگوریتم ژنتیک با C
خروجی:
پیادهسازی الگوریتم ژنتیک با C#
خروجی:
پیادهسازی الگوریتم ژنتیک با C++
خروجی:
BBQYCNLDIHG RWEXN PNGFTCMS: -203 ECPZEOLCHFJBCXTXFYLZQPDDQ KP: -177 HBSBGMKEEIM BUTUGWKWNRCGSZNN: -150 EEUCGNKDCHN RSSITKZPRBESYQK: -134 GBRFGNKDAINX TVRITIZPSBERXTH: -129 JEUFILLDDGNZCWYRIWFWSUAERZUI: -120 JESGILIGDJOZCWXRIWFVSXZESXXI: -109 JCSHILIIDIOZCTZOIUIVVXZEUVXI: -93 ........... NETHINKS IT JS LHKE A WEASEL: -3 NETHINKS IT JS LIKE A WEASEL: -2 NETHINKS IT JS LIKE A WEASEL: -2 NETHINKS IT JS LIKE A WEASEL: -2 NETHINKS IT JS LIKE A WEASEL: -2 NETHINKS IT JS LIKE A WEASEL: -2 NETHINKS IT JS LIKE A WEASEL: -2 METHINKS IT JS LIKE A WEASEL: -1 METHINKS IT JS LIKE A WEASEL: -1 METHINKS IT JS LIKE A WEASEL: -1 final string: METHINKS IT IS LIKE A WEASEL
پیادهسازی الگوریتم ژنتیک با جاوا
خروجی:
100: MEVHIBXSCG TP QIK FZGJ SEL, fitness: 13, rate: 0.4875 200: MEBHINMSVI IHTQIKW FTDEZSWL, fitness: 15, rate: 0.42250000000000004 300: METHINMSMIA IHUFIKA F WEYSEL, fitness: 19, rate: 0.29250000000000004 400: METHINSS IT IQULIKA F WEGSEL, fitness: 22, rate: 0.195 METHINKS IT IS LIKE A WEASEL, 492
پیادهسازی الگوریتم ژنتیک با متلب
اجرا:
خروجی:
Target fitness is 28 1: MVEOCXXFBYD SFCMJQNWTPM PCVA - Fitness: 2 2: MEEOCXXFBYD SFCMJQNWTPM PCVA - Fitness: 3 3: MEEHCXXFBYD SFCMJXNWTPM ECVA - Fitness: 4 4: MEEHCXXFBYD SFCMJXNWTPM ECVA - Fitness: 4 5: METHCXAFBYD SFCMJXNWXPMARPVA - Fitness: 5 6: METHCXAFBYDFSFCMJXNWX MARSVA - Fitness: 6 7: METHCXKFBYDFBFCQJXNWX MATSVA - Fitness: 7 8: METHCXKFBYDFBF QJXNWX MATSVA - Fitness: 8 9: METHCXKFBYDFBF QJXNWX MATSVA - Fitness: 8 10: METHCXKFUYDFBF QJXNWX MITSEA - Fitness: 9 20: METHIXKF YTBOF LIKN G MIOSEI - Fitness: 16 30: METHIXKS YTCOF LIKN A MIOSEL - Fitness: 19 40: METHIXKS YTCIF LIKN A MEUSEL - Fitness: 21 50: METHIXKS YT IS LIKE A PEUSEL - Fitness: 24 100: METHIXKS YT IS LIKE A WEASEL - Fitness: 26 150: METHINKS YT IS LIKE A WEASEL - Fitness: 27 195: METHINKS IT IS LIKE A WEASEL - Fitness: 28
پیادهسازی الگوریتم ژنتیک با پایتون
خروجی:
#100 , fitness: 50.0%, 'DVTAIKKS OZ IAPYIKWXALWE CEL' #200 , fitness: 60.7%, 'MHUBINKMEIG IS LIZEVA WEOPOL' #300 , fitness: 71.4%, 'MEYHINKS ID SS LIJF A KEKUEL' #378 , fitness: 100.0%, 'METHINKS IT IS LIKE A WEASEL'
فیلم آموزش تئوری و عملی الگوریتم ژنتیک و پیاده سازی آن در MATLAB
در صورتی که به موضوع الگوریتم ژنتیک علاقهمند هستید، میتوانید دوره ویدیویی آموزش این الگوریتم و پیادهسازی آن در متلب را در وب سایت فرادرس مشاهده کنید. در این دوره آموزشی، ابتدا مروری بر مبانی علم ژنتیک و منشأ الهام الگوریتمهای تکاملی و الگوریتمهای ژنتیک انجام شده است. سپس، اجزا و ساختار پایه الگوریتمهای ژنتیک معرفی شده است. در گام بعدی، انواع شرایط خاتمه در روشهای بهینهسازی و الگوریتمهای عددی، انواع ساختارهای ممکن برای تلفیق و انتخاب اعضای جمعیت جدید، انواع روشهای انتخاب والدین و انواع عملگرها برای مسائل مختلف مورد بررسی قرار گرفتهاند. در ادامه، پیادهسازی الگوریتم ژنتیک باینری و پیادهسازی الگوریتم ژنتیک پیوسته، در متلب انجام شده است. همچنین، مسأله مکانیابی هاب، مسأله حمل و نقل، مسأله تخصیص درجه دو یا QAP، مسأله شناسایی سیستم و مدلسازی سیستمهای غیر خطی و روش حل آنها با استفاده از الگوریتم ژنتیک، بیان و در متلب پیادهسازی شده است. مدرس این دوره آموزشی دکتر سید مصطفی کلامی هریس و مدت زمان دوره 14 ساعت و 20 دقیقه است.
- برای دیدن فیلم آموزش تئوری و عملی الگوریتم ژنتیک + اینجا کلیک کنید.
جمعبندی
الگوریتمهای ژنتیک، به راحتی در دامنه وسیعی از مسائل، از جمله مسائل بهینهسازی نظیر «مسأله فروشنده دورهگرد» (Travelling Salesman Problem) و مسائل مرتبط با «برنامهریزی» (Scheduling)، میتوانند مورد استفاده قرار بگیرند. نتایج حاصل از الگوریتم ژنتیک برای برخی از مسائل ممکن است بسیار خوب و برای برخی دیگر از مسائل، ممکن است بسیار ضعیف باشد. اگر تنها از عملگر جهش در الگوریتم ژنتیک استفاده شود، الگوریتم بسیار کند میشود. استفاده از عملگر ترکیب، سبب سرعت بخشیدن به فرایند همگرایی در الگوریتم ژنتیک خواهد شد.
مشکل بهینه محلی در الگوریتم ژنتیک بسیار شایع است. در حالتی که الگوریتم در بهینه محلی قرار بگیرد، استفاده از عملگر جهش سبب میشود تا جوابهای بدتری نسبت به بهینه محلی تولید شود. با این حال، برای فرار از دام بهینه محلی میتوان از عملگر ترکیب استفاده کرد. البته، از آنجایی که جهش یک فرایند کاملا تصادفی است، این امکان نیز وجود دارد که جهشهای بزرگی در کروموزومها ایجاد شوند و آن کروموزومها یا جوابهای کاندید از بهینه محلی خارج شوند.
در آینده، ممکن است شاهد توسعه الگوریتمهای تکاملی باشید که برای حل مسائل خاص مورد استفاده قرار بگیرند. این امر، نقض اصول پیادهسازی الگوریتم ژنتیک است که با هدف استفاده همه منظوره و بدون در نظر گرفتن دامنه مسائل قابل حل، توسعه داده شدهاند.
با این حال، چنین گرایشی در توسعه الگوریتمهای تکاملی ممکن است منجر به تولید سیستمهای تکاملی به مراتب قویتر شود.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای الگوریتمهای بهینهسازی هوشمند
- آموزش تئوری و عملی الگوریتمهای ژنتیک
- مجموعه آموزشهای الگوریتمهای ژنتیک و محاسبات تکاملی
- الگوریتم بهینه سازی فاخته — از صفر تا صد
- رویکرد هوش ازدحامی با استفاده از کلونی زنبور عسل مصنوعی برای حل مسائل بهینهسازی
- الگوریتم کلونی مورچگان — از صفر تا صد
- درس هوش مصنوعی | مفاهیم پایه به زبان ساده — منابع، کتاب و فیلم آموزشی
^^













سلام
مطلب جامع و مفیدی بود اما بنده بطور دقیق متوجه کاربرد این الگوریتم نشدم که مثلا با یادگیری این الگوریتم بطور مثال در صنعت نفت و گاز چه اقدامی میتوانیم انجام دهیم و اینکه این الگوریتم چگونه دراین صنعت میتواند به ما کمک کند و آیا پیشنهاد میدهید که این الگوریتم را مطالعه کرده و آموزش ببینم؟
تشکر از وقتی که قرار دادید
ایام به کام
با سلام خدمت شما همراه گرامی؛
الگوریتم ژنتیک در صنعت نفت و گاز برای حل مسائل پیچیده و بهینهسازی فرآیندها کاربرد دارد. به طور خلاصه، GA در موارد زیر کمک میکند:
۱- حفاری و تولید: بهینهسازی مسیر مته، نرخ تولید و پارامترهای چاه.
۲- اکتشاف: تفسیر دادههای لرزهای، مدلسازی مخزن و تخمین پارامترهای مخزن.
۳- مدیریت زیرساختها: بهینهسازی شبکههای لوله، برنامهریزی تعمیر و نگهداری و مدیریت ریسک.
به طور کلی، GA به بهبود کارایی، کاهش هزینهها و افزایش ایمنی در صنعت نفت و گاز کمک میکند.
از بازخورد و همراهی شما با مجله فرادرس سپاسگزاریم.
الگوریتم بهینه سازی NSGA ii رو شرحش رو میگذارید لطفا؟
در بیان پایههای تولثد کروموزوم از دی ان آ که چهذ مورد هست یک اشتباه صورت گرفته و جای T و G اشتباه نوشته شده است.
سلام
یعنی هر چی زمان میگذره انسان های بهتری متولد میشن؟
با سلام و احترام؛
صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم.
این مورد اصلاح شد.
برای شما آرزوی سلامتی و موفقیت داریم.
سلام
فوق العاده بود.
سلام
من یه سوال داشتم اینکه روشهای انتخاب جمعیت جدید تو این الگوریتم ژنتیک به چه صورتی هست اگه میشه لطفا توضیح بدید ممنون میشم؟
با سلام، ببخشید یه سوال درباره الگوریتم ژنتیک داشتم اونم اینکه در توابع چند هدفه که الگوریتم تعدادی از توابع رو بهینه کرده، تکلیف توابعی که بهینه نشدن چیه و چطور باید اونا رو با این الگوریتم بهینه کرد؟ ممنون میشم راهنمایی بفرمایید برای پایان نامه ام میخوام
سلام .ابتدا از طریق تابع براندازی رشته های براندازه تر انتخاب میشن و باقی رشته ها از جمعیت حذف میشن سپس سه عملگر ژنتیک روی آن ها عمال میشن و به جمعیت کلی به به عنوان جمعیت جدید اضافه میشن
سلام سوالی داشتم از محضرتون چرا در الگوریتم ژنتیک چند هدفه با تغییر تعداد اعضای جمعیت تعداد نقاط پارتو تغییر میکنه؟
سلام در مسئله مطرح شده متغیر ها بین 0 تا 6 تغییر میکنند که به اشتباه در صورت سوال بین 0 تا 0 ذکر شده
با سلام و احترام؛
صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم. اصلاحات لازم انجام شد.
برای شما آرزوی سلامتی و موفقیت داریم.
در انتهای جمله “اما اگر طول رشته به 5 افزایش پیدا کند، دقت قابل استحصال توسط کدبندی پنج بیتی، تقریبا برابر با یک شانزدهم (1/32) فضای جستجوی مسأله خواهد شد.” باید یک سی و دوم قید شود که اشتباه تایپی دارد.
با سلام؛
از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم. اصلاحات لازم انجام شد.
پیروز، شاد و تندرست باشید.
با سلام و احترام .
ممنون از مطلب عالی تون .
فقط من نیاز دارم که منابع این مطلب شمارو مطالعه کنم . میشه منابعش رو معرفی کنید ؟
سلام، وقت شما بخیر؛
منابع تمامی مجله فرادرس در انتهای آنها و بعد از بخش معرفی مطالب و آموزشهای مشابه ذکر شده است.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
خیلی عالی بود و همچنین کامل.
خیلی عالی و کامل بود، ممنون.