آزمون های فرض آماری در یادگیری ماشین – اصول و مفاهیم اولیه

در دیگر نوشته‌های فرادرس مانند آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات با مفاهیم اولیه «آزمون فرض آماری» (Statistical Hypothesis Testing) آشنا شده‌اید. همچنین در بعضی از مطالب وبلاگ فرادرس با کاربردهای آزمون فرض مثلا در آزمون برابری میانگین یا برابری واریانس در نمونه‌های تصادفی برخورد داشته‌اید. در این نوشتار به بررسی آزمون فرض آماری در «یادگیری ماشین» (Machine Learning) پرداخته و برای انجام محاسبات نیز از زبان برنامه نویسی «پایتون» (Python) کمک خواهیم گرفت. این نوشتار در دو قسمت تهیه شده است. در قسمت اول نوشتار، به معرفی اصطلاحات آزمون آماری پرداخته شده و در قسمت دوم با عنوان آزمون فرض آماری در یادگیری ماشین --- پیاده سازی با پایتون به همراه کدهای پایتون به انجام آزمون‌هایی آماری خواهیم پرداخت. آزمون‌هایی که در این دو نوشتار به آن‌ها اشاره خواهیم داشت مطابق فهرست زیر هستند.

• آزمون تک نمونه‌ای برای جامعه نرمال با فرض نامعلوم بودن واریانس (One sample T-test)
• آزمون‌های مقایسه میانگین دو جامعه نرمال با فرض نامعلوم بودن واریانس (Two-sample T test)
• آزمون‌های مقایسه میانگین دو جامعه نرمال با فرض معلوم بودن واریانس (Two-sample Z test)
• آزمون تحلیل واریانس (One Way F-test ،Anova)
• آزمون F دو طرفه (Two Way F-Test)
• آزمون کای ۲ (Chi-Square Test)

از آنجایی که در بسیاری از روش‌های آزمون فرض آماری از مقدار احتمال (p-Value) استفاده می‌شود، مطالعه نوشتار مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری ضروری به نظر می‌رسد. همچنین نحوه محاسبه احتمال برای توزیع نرمال توسط جدول‌های این توزیع در نوشتار توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها قابل مطالعه است. از طرفی با خواندن مطلب توزیع های آماری F و T — مفاهیم و کاربردها از خصوصیات توزیع T و F که در این نوشتار از آن‌ها استفاده خواهیم کرد آگاهی پیدا می‌کنید. در نتیجه خواندن این مطالب نیز خالی از لطف نیست.

آزمون های فرض آماری در یادگیری ماشین

آشنایی با آمار و شیوه‌های مختلف به کارگیری آن در یادگیری ماشین، برای مبتدیان یا حتی کسانی که در امر داده‌کاوی با تجربه هستند، ضروری است. یکی از روش‌های مرسوم آماری در یادگیری ماشین، آزمون فرض آماری است. براساس این روش در مورد توزیع یا پارامترهای توزیع داده‌های جمع‌آوری شده، دست به قضاوت می‌زنیم.

البته مشخص است که با توجه به انجام تحلیل روی نمونه تصادفی به جای جامعه آماری، نتایج یا تصمیمات صورت گرفته، حتما با خطا نیز همراه خواهند بود. به کمک آزمون‌های آماری و داده‌های حاصل از نمونه‌گیری، سعی داریم این خطا حداقل ممکن باشد تا به نتایج نسبتا دقیقی برسیم.

تعریف‌های اولیه در آزمون فرض آماری

یکی از روش‌های آماری برای اتخاذ تصمیم در مورد داده‌ها، استفاده از «آزمون فرض آماری» (Statistical Hypothesis Testing) است. هنگام استفاده از آزمون‌های آماری باید بدانیم چه زمانی از چه آزمون استفاده و نتایج حاصل را به چه شکل تفسیر کنیم. به این منظور در ابتدا با اصطلاحاتی که در آزمون فرض آماری به کار می‌رود، آشنا شده و سپس در قسمت دوم این نوشتار، با استفاده از کدهای پایتون به بررسی داده‌ها و انجام آزمون فرض آماری خواهیم پرداخت.

هر آزمون فرض آماری از دو فرضیه تشکیل شده است. «فرض صفر» (Null Hypothesis) که به صورت $$H_0$$ نشان داده می‌شود و «فرض مقابل» (Alternative Hypothesis) که با علامت $$H_A$$ مشخص می‌شود. البته گاهی فرض مقابل را «فرض یک» نیز می‌نامند و آن را به صورت $$H_1$$ نشان می‌دهند. هر یک از این فرضیه‌ها، توصیفی برای پارامتر یا توزیع جامعه آماری هستند.

فرض صفر (Null Hypothesis)

در آزمون فرض آماری، فرض صفر بیانگر وضعیت جاری یا تصور موجود برای جامعه آماری است. معمولا عدم رابطه بین دو جامعه یا دو پدیده احتمالی در فرض صفر قرار می‌گیرد. برای مثال می‌توان تصور کرد که در یک کارخانه تولید خودرو، متوسط خودورهای تولیدی در روز برابر با ۵۰ است. البته این ادعای کارخانه است. اگر $$\mu$$ میانگین تولیدات این کارخانه در روز باشد، این گزاره را به بیان ریاضی به صورت زیر می‌نویسیم.

$$\large H_0: \mu = 50$$

یک تحلیل‌گر داده با استفاده از نمونه‌‌گیری در روزهای مختلف سعی دارد این گزاره یا ادعا را بسنجد و فرض صفر (نظر کارخانه تولید کننده) را تایید یا رد کند. معمولا در تحقیقات آماری سعی بر رد فرض صفر است در غیر اینصورت توجیهی برای اجرای طرح آماری و انجام آزمون فرض آماری وجود ندارد.

نکته: البته گاهی برای تایید فرض صفر نیز طرح آماری و آزمون فرض صورت می‌گیرد ولی نتیجه‌ای که حاصل می‌شود، بیانگر وضع موجود است. باید توجه داشت که با استفاده یک نمونه آماری نمی‌توان فرض صفر را قبول کرد، بلکه فقط می‌توان شواهدی مبنی بر تایید فرض صفر داشت. در حالیکه هنگام رد فرض صفر، می‌توان نمونه به کار گرفته شده در آزمون فرض را یک مثال نقض برای حکمی که در فرض صفر نوشته شده در نظر گرفت.

فرض مقابل (Alternative Hypothesis)

گزاره یا وضعیتی که ادعای محقق را نشان می‌دهد، فرض مقابل می‌نامیم. ممکن است این گزاره به صورت نقیض فرض صفر نوشته شده باشد. به هر حال باید توجه داشت که فرض مقابل نباید دارای نقاط اشتراکی با فرض صفر باشد. به عنوان مثال می‌توان با توجه به نظر کارخانه تولید کننده خودرو، فرض مقابل را به یکی از صورت‌های زیر نوشت:

• میزان تولید در روز این کارخانه کمتر از ۵۰ دستگاه است.

$$\large H_A: \mu < 50$$

• میزان تولید در روز این کارخانه بیشتر از ۵۰ دستگاه است.

$$\large H_A: \mu > 50$$

• میزان تولید در روز این کارخانه مخالف ۵۰ دستگاه است.

$$\large H_A: \mu \neq 50$$

خطای نوع اول (Type I Error)

هنگامی که بوسیله نمونه تصادفی رای به رد فرض صفر می‌دهیم، ممکن است دچار خطا شده باشیم. این نوع خطا را نوع اول می‌نامند. به این ترتیب می‌توان احتمال مرتکب شدن خطای نوع اول را به صورت زیر نشان داد. در اینجا منظور از reject رد کردن فرض و correct به معنی صحیح بودن فرض است.

$$\large \alpha =P(reject\;H_0| H_0\; is\;correct)$$

خطای نوع دوم (Type II Error)

اگر در آزمون فرض آماری فرض صفر، رد نشود در حالیکه در واقعیت گزاره بیان شده در فرض مقابل صحیح باشد، باز هم مرتکب خطا شده‌ایم. این خطا را به نام خطای نوع دوم شناخته و احتمال رخداد آن را با $$\beta$$ نشان می‌دهند.

$$\large \beta= P(reject\;H_A |H_0 \; is \; not \; correct)$$

سطح معنی‌داری یا آزمون (Level of Significant)

میزان دقت یا درصد خطای که در آن به رد فرض صفر رای می‌دهیم، سطح آزمون گفته می‌شود. معمولا با توجه به استفاده از نمونه تصادفی، میزان دقت هرگز به ۱۰۰٪ نخواهد رسید. به همین علت در حالت کلی خطا را ۵٪ یا 0.05 و دقت را 95٪ یا 0.95 در نظر می‌گیرند. به این ترتیب، سطح آزمون نشان می‌دهد که فرض صفر با حداکثر چه خطای رد شده است. در حقیقت سطح آزمون مقدار احتمال خطای نوع اول است. انتظار داریم که این احتمال بسیار کم باشد زیرا این احتمال نشان‌دهنده رد فرض صفر به ناحق است. به این ترتیب سطح آزمون $$\alpha$$ و دقت آزمون به صورت $$۱-\alpha$$ در نظر گرفته می‌شود. از طرف دیگر توان آزمون (صحت آزمون‌) نیز برابر با $$1-\beta$$ است.

آزمون یک طرفه و دو طرفه

اگر ناحیه رد فرض صفر در یک طرف توزیع نمونه‌ای قرار بگیرد، آزمون را یکطرفه می‌گویند. معمولا در این آزمون‌ها فرض صفر به صورت تساوی و فرض‌ مقابل به صورت بزرگتر یا کوچکتر نوشته می‌شوند. به تصویرهای زیر که مربوط به توزیع نمونه‌ای آماره آزمون است، توجه کنید. در تصویر زیر ناحیه مربوط به رد فرض صفر در سمت چپ قرار دارد. اگر $$T$$ آماره آزمون (تابعی از نمونه تصادفی که براساس آن تصمیم به رد فرض صفر می‌گیریم) و $$c$$ نیز تعیین کننده ناحیه بحرانی باشد، مشخص است که فرض مقابل به صورت مثلا $$H_A: \mu$$ نوشته شده است و ناحیه بحرانی نیز به صورت $$T$$ در نظر گرفته شده است.

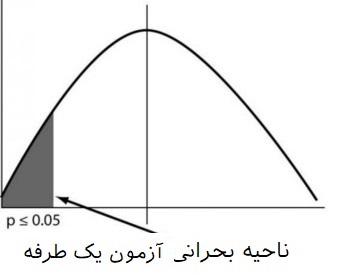
همچنین ممکن است که ناحیه بحرانی در سمت راست نمودار توزیع قرار گیرد. در این صورت فرض مقابل به صورت مثلا $$H_A: \mu >a$$ نوشته شده است و ناحیه بحرانی نیز به صورت $$T>c$$ خواهد بود. این حالت در تصویر زیر قابل مشاهده است.

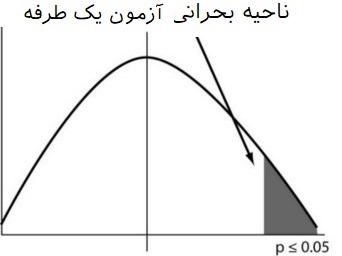
آزمون دو طرفه

در آزمون دو طرفه، فرض مقابل به صورت متمم فرض صفر است. بنابراین اگر فرض صفر به صورت $$H_0: \mu=a$$ باشد، فرض مقابل به شکل $$H_A: \mu \neq a$$ نوشته خواهد شد. در نتیجه ناحیه بحرانی به شکل $$|T|$$ در نظر گرفته می‌شود. چنین حالتی روی نمودار توزیع آماره آزمون مطابق زیر نمایش داده خواهد شد.

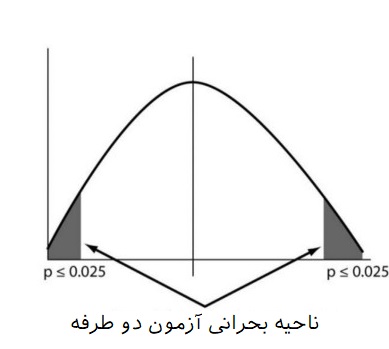
مقدار احتمال (p-Value)

در یک آزمون فرض، مقدار احتمال (p-Value) برابر با کمترین مقداری از سطح معنی‌داری (significance level) یا همان احتمال خطای نوع اول است، که به موجب آن (با توجه به مقدارهای اندازه‌گیری شده از نمونه‌ها)، فرض صفر رد می‌شود. به این ترتیب، قاعده‌ای برای انجام آزمون فرض آماری بوسیله مقدار احتمال در نظر گرفته شده است. این قاعده بیان می‌کند که فرض صفر رد می‌شود، هر گاه مقدار احتمال (p-Value) از $$\alpha$$ (احتمال خطای نوع اول) کوچکتر باشد. به این ترتیب در آزمون فرض آماری، با در نظر گرفتن سطح آزمون برابر با 0.05 و محاسبه مقدار احتمال می‌توان نسبت به رد یا عدم رد فرض صفر رای داد.

فیلم آموزش مقدماتی استنباط و آمار بیزی در فرادرس

کلیک کنید

نکته: از این قاعده بدون در نظر گرفتن فاصله مقدار احتمال با خطای نوع اول به کار می‌رود. به این معنی که اگر برای مثال سطح آزمون (احتمال رد فرص صفر) برابر با 0.05 در نظر گرفته شود و مقدار احتمال برابر با 0.01 باشد فرض صفر رد خواهد شد. همچنین اگر مقدار احتمال برابر با 0.04 نیز باشد باز هم فرض صفر رد می‌شود. پس مشخص است که نزدیکی یا دوری مقدار احتمال از سطح آزمون، بر روی تصمیمی که در مورد فرض صفر گرفته می‌شود، تاثیرگذار نیست.

به کارگیری مقدار احتمال در آزمون فرض

فرض کنید یک سکه را برای مشخص کردن سالم بودن آن پرتاب کرده‌ایم. یعنی می‌خواهیم بسنجیم که احتمال مشاهده شیر برابر با 0.5 است یا خیر.

به این ترتیب می‌توان فرضیات مربوط به آزمون فرض آماری را به صورت زیر نوشت.

$$\large \begin{cases}H_0: & p = 0.5\\H_A: & p \neq 0.5\end{cases}$$

حال با در نظر گرفتن میزان خطا یا سطح آزمون $$\alpha=0.05$$ می‌خواهیم آزمون را اجرا کنیم. در نتیجه اگر $$X$$ تعداد شیرهای مشاهده شده با توزیع دو جمله‌ای در نظر گرفته شود، فرض صفر رد می‌کنیم، اگر $$X$$ کمتر از نصف تعداد پرتاب‌ها باشد. در نتیجه مقدار احتمال به صورت زیر محاسبه می‌شود.

اگر در دو بار پرتاب سکه، هیچ شیری مشاهده نشود:

$$\large \displaystyle P(X=0|p=0.5) = {2\choose 0}p^0(1-p)^{1-0}=(1-0.5)^1=0.5$$

پس در این حالت با توجه به قاعده تصمیم بوسیله مقدار احتمال، دلیلی برای رد فرض صفر وجود ندارد.

اگر در چهار بار پرتاب سکه، سه شیر مشاهده شود:

$$\large \displaystyle P(X= 3|p=0.5) ={4 \choose 3} p^3(1-p)^{4-1}=0.5^3(1-0.5)^1=0.5^4=0.0625$$

با توجه به اینکه $$p-value=0.0625>0.05= \alpha$$ باز هم قادر به رد فرض صفر نیستیم.

حالتی را در نظر بگیرید که در ده‌ بار پرتاب سکه دو بار شیر دیده شده است. پس مقدار احتمال به صورت زیر قابل محاسبه است.

$$\large \displaystyle P(X= 2|p=0.5) ={10 \choose 2} p^2(1-p)^{10-2}=120\times (0.5)^10=0.044$$

از آنجایی که مقدار احتمال کمتر از سطح آزمون ($$\alpha$$) است، فرض صفر در اینجا رد خواهد شد.

آماره آزمون و درجه آزادی (Degree of Freedom)

به منظور مشخص کردن ناحیه بحرانی احتیاج به تابعی از نمونه تصادفی داریم. توزیع احتمالاتی این آماره نباید مرتبط با پارامتری باشد که در آزمون آماری به کار رفته است. به کمک ترکیبی از آماره آزمون و پارامتر، ناحیه بحرانی تشکیل می‌شود که مبنای محاسبه احتمال خطای نوع اول و همچنین مقدار احتمال است.

ممکن است برای محاسبه یا تعیین توزیع آماره آزمون، مجبور به برآورد بعضی از پارامترهای دیگر باشیم. این کار تغییر پذیری (درجه آزادی) مقدارهای نمونه را کاهش می‌دهد. برای مثال فرض کنید که میانگین چهارعدد مشخص (برآورد) شده باشد. پس چهار عدد داریم که مجموعشان از قبل مشخص است. اگر بخواهیم همه اعداد را آزادانه تغییر دهیم، بطوری که مجموعشان (میانگین) ثابت باشد، لازم است که روی یک از مقدارها محدودیت داشته باشیم.

$$\large x_1+x_2+x_3+x_4=a\rightarrow x_1=a-(x_2+x_3+x_4)$$

همانطور که دیده می‌شود مقدار $$X_1$$ برحسب مقدار جمع کل و بقیه مقدارها، قابل محاسبه است. در نتیجه مقدار $$X_1$$ آزادانه قابل انتخاب نیست. در چنین حالتی می‌گوییم، درجه آزادی برای داده‌ها (با توجه به برآورد میانگین یا مجموعشان) مقدار سه است. یعنی یک درجه از آزادی این چهار عدد کم شده است.

مشخص است که این محدودیت در تعیین توزیع آماره آزمون نیز دیده می‌شود. در ادامه خواهید دید که در بعضی از مواقع برای آماره‌های آزمونی که دارای پارامتری به صورت درجه آزادی هستند، به علت برآورد یکی از پارامترهای توزیع (مثلا میانگین) یک درجه از درجه آزادی توزیع کاسته می‌شود. آماره‌های آزمون با توزیع‌های آماره‌های t و F و همچنین کای ۲ از این گونه هستند.

خلاصه و جمع‌بندی

در قسمت اول از این نوشتار به معرفی مشخصه‌ها و اصطلاحات اصلی مرتبط با آزمون آماری پرداختیم. در بخش یا قسمت دوم از این مطلب با استفاده از زبان برنامه‌نویسی پایتون به انجام آزمون‌های آماری پرداخته خواهد شد. برای کسب اطلاعات بیشتر در زمینه‌ انجام آزمون‌های آماری می‌توانید به مطلب آزمون تی (T Test) در R — راهنمای کاربردی یا آزمون میانگین نمونه تکی در SPSS — راهنمای کاربردی مراجعه کنید.

اگر مطلب بالا برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های SPSS
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آزمون آماری و پی مقدار (p-value)
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات

^^