آزمون های فرض آماری در یادگیری ماشین — پیاده سازی با پایتون

در قسمت اول این نوشتار با عنوان آزمون های فرض آماری در یادگیری ماشین — اصول و مفاهیم اولیه، با مفاهیم اولیه «آزمون های فرض آماری» (Statistical Hypothesis Testing) آشنا شده‌اید. در این قسمت با استفاده از مفاهیم فراگرفته شده و به کمک توابع موجود در زبان برنامه نویسی پایتون، چند مثال کاربردی در زمینه آزمون فرض آماری را حل خواهیم کرد. در این میان برای حل مثال‌ها، از آزمون‌ T، آزمون Z، تحلیل واریانس و آزمون کای ۲ استفاده می‌شود.

آزمون های فرض آماری در پایتون

در این نوشتار به بررسی چند روش آزمون و توابع موجود در کتابخانه‌های پایتون که بیشتر در زمینه آزمون فرض در مورد میانگین و مقایسه آن در بین چندین جامعه است می‌پردازیم که همگی از نوع آزمون‌های پارامتری هستند. البته در بخش ناپارامتری نیز به بررسی آزمون کای ۲ خواهیم پرداخت که مربوط به استقلال دو سری یا گروه داده طبقه‌ای است.

فیلم آموزش برنامه نویسی پایتون Python – مقدماتی در فرادرس

کلیک کنید

آزمون‌های تی (T-test)

این گروه از آزمون‌ها به بررسی برابری میانگین در بین یک یا دو جامعه مستقل یا وابسته می‌پردازد. در ادامه حالت‌هایی از این گونه آزمون‌ها را ارائه خواهیم داد که آماره آزمون آن‌ها دارای توزیع T است.

آزمون تی تک نمونه‌ای (One Sample T-test)

از این آزمون برای مقایسه میانگین یک جامعه با توزیع نرمال با مقدار ثابت استفاده می‌شود. ابتدا حدسی برای میانگین جامعه زده شده که این مقدار حدسی در فرض صفر قرار می‌گیرد. با استفاده از یک نمونه تصادفی سعی داریم نشان دهیم که میانگین جامعه نرمال با مقدار حدس زده شده یکسان نیست.

$$\large \begin{cases} H_0: \mu =\mu_0 \\ \large H_1: \mu \neq  \mu_0\\ \end{cases}$$

آماره آزمون برای چنین حالتی به صورت زیر نوشته می‌شود.

$$\large T=\dfrac{\overline{X}-\mu_0}{\frac{s}{\sqrt{n}}}$$

منظور از $$\overline{X}$$ میانگین نمونه‌ای و $$s$$ نیز انحراف استاندارد نمونه‌ای است. همچنین $$n$$ بیانگر تعداد نمونه‌ها است. واضح است که این آماره دارای توزیع t است. ولی از آنجایی که میانگین جامعه برآورد شده است، یک واحد از درجه آزادی کاسته می‌شود. بنابراین آماره آزمون دارای توزیع t با n-1‌ درجه آزادی است.

مثال: فرض بر این است که میانگین سن دانشجویان مقطع دکتری برابر با ۳۰ سال است. با استفاده از یک نمونه چهارده‌تایی، سعی داریم آزمون آماری که به صورت زیر نوشته شده است را مورد بررسی قرار دهیم.

$$\large \begin{cases}H_0 :& \mu =30\\H_A:& \mu \neq 30 \end{cases}$$

در جدول زیر این مقادیر دیده می‌شود.

نکته: فرض کنید این مقدارهای در یک فایل متنی به نام ages.csv ثبت شده‌اند.

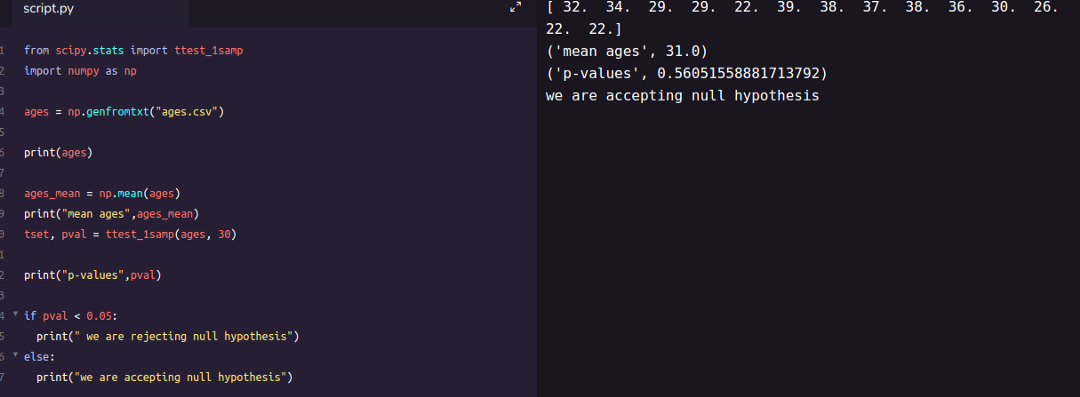
کد زیر به منظور محاسبه و اجرای آزمون فرض در روش t-test تهیه شده است. همانطور که دیده می‌شود تابع ttest_1samp از کتابخانه scipy.stats در پایتون وظیفه انجام آزمون را دارد. مشخص است که پارامتر دوم در این تابع همان مقدار حدسی برای میانگین ($$\mu_0$$) است.

1from scipy.stats import ttest_1samp
2import numpy as np
3ages = np.genfromtxt(“ages.csv”)
4print(ages)
5ages_mean = np.mean(ages)
6print(ages_mean)
7tset, pval = ttest_1samp(ages, 30)
8print(“p-values”,pval)
9if pval < 0.05:    # alpha value is 0.05 or 5%
10   print(" we are rejecting null hypothesis")
11else:
12  print("we are accepting null hypothesis")

خروجی برای چنین برنامه‌ای، در تصویر زیر دیده می‌شود. با توجه به بزرگتر بودن مقدار احتمال (p-value=0.5605) از مقدار $$\alpha=0.05$$، فرض صفر در این مثال رد نخواهد شد.

آزمون تی دو جامعه مستقل (Two Sample T-test)

فرض کنید دو جامعه A و B یا دو سری داده در دسترس است. می‌خواهیم برای نمونه‌های تصادفی از هر دو جامعه، تصمیم بگیریم که آیا میانگین این دو جامعه با یکدیگر برابر هستند یا خیر.

فیلم آموزش ساختمان داده ها با پایتون در فرادرس

کلیک کنید

در چنین حالتی آزمون فرض به صورت زیر نوشته خواهد شد:

$$\large \begin{cases}H_0: \mu_A =\mu_B \\H_A: \mu_A \neq \mu_B\end{cases}$$

آماره آزمون برای آزمون تی دو جامعه مستقل به شکل زیر نوشته می‌شود:

$$\large T=\dfrac{\overline{x}_A-\overline{x}_B}{\sqrt{\frac{S^2}{n_A}+\frac{S^2}{n_B}}}$$

از آنجایی که در این آماره از برآورد دو میانگین جامعه استفاده شده، درجه آزادی آن برابر با $$n_A+n_B-2$$‌ خواهد بود.

مثال: می‌خواهیم مشخص کنیم که میانگین بارش در دو هفته از فصل پاییز با یکدیگر برابر هستند یا خیر. از آنجایی که میزان بارش‌ها در هر هفته از یکدیگر مستقل هستند، باید از آزمون میانگین t مستقل استفاده کنیم. فرض کنید که میزان بارش هفته اول در فایل week1.csv و بارش هفته دوم نیز در فایل week2.csv ثبت شده است. با استفاده از کد‌های زیر که به زبان پایتون نوشته شده‌اند، اجرای چنین آزمون میسر خواهد بود.

1from scipy.stats import ttest_ind
2import numpy as np
3week1 = np.genfromtxt("week1.csv",  delimiter=",")
4week2 = np.genfromtxt("week2.csv",  delimiter=",")
5print(week1)
6print("week2 data :-\n")
7print(week2)
8week1_mean = np.mean(week1)
9week2_mean = np.mean(week2)
10print("week1 mean value:",week1_mean)
11print("week2 mean value:",week2_mean)
12week1_std = np.std(week1)
13week2_std = np.std(week2)
14print("week1 std value:",week1_std)
15print("week2 std value:",week2_std)
16ttest,pval = ttest_ind(week1,week2)
17print("p-value",pval)
18if pval <0.05:
19  print("we reject null hypothesis")
20else:
21  print("we accept null hypothesis")

مشخص است که اجرای این آزمون توسط تابع ttest_ind از کتابخانه scipy.stats صورت گرفته است. پس از اجرای این برنامه خروجی ممکن است به صورت زیر ظاهر شود. البته برای محاسبه شاخص‌های آماری نظیر انحراف استاندارد و میانگین نیز از توابع mean و std از کتابخانه numpy کمک گرفته‌ایم.

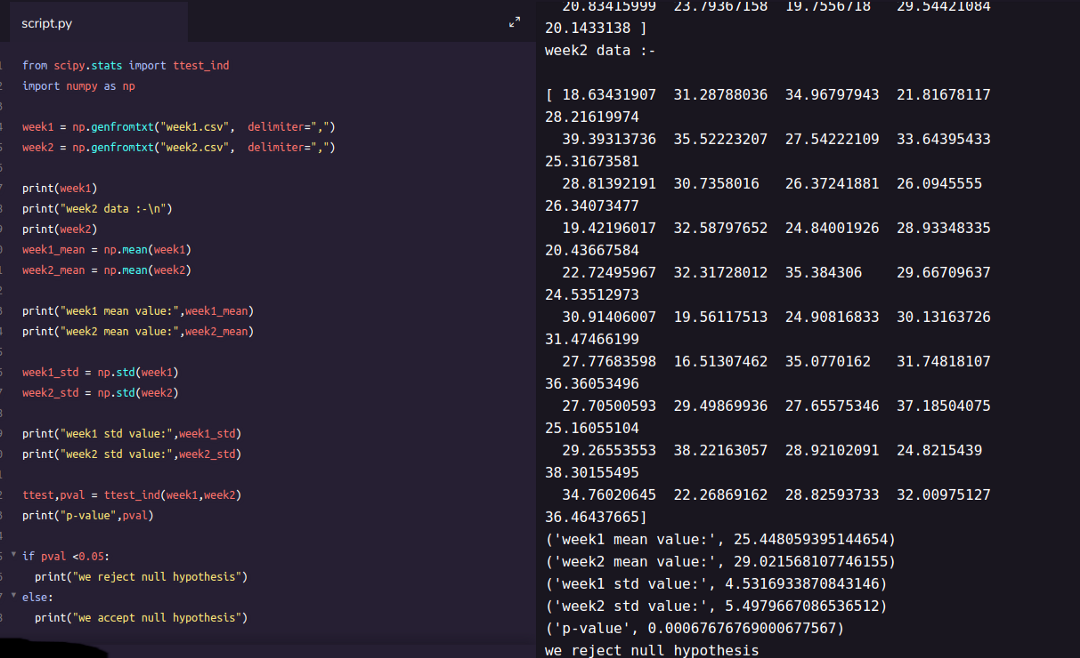
با توجه به مقدارهای محاسبه شده برای میانگین و انحراف استاندارد دو جامعه و مقدار احتمال (p-value=0.000676)، مشخص است که فرض صفر در سطح آزمون 0.05 رد می‌شود. پس به نظر می‌رسد که مقدار بارندگی در هفته اول و دوم تفاوت داشته و در هفته دوم متوسط بارش بیشتر از هفته اول است. این نتیجه را به زبان آماری به این صورت بیان می‌کنیم: «اختلاف میانگین بارندگی بین هفته اول و دوم، از لحاظ آماری معنی‌دار است.»

آزمون تی برای مقایسه میانگین در زوج مشاهدات (Paired Sample T-test)

از آنجایی که در این آزمون از زوج مشاهدات استفاده می‌شود، می‌توان آن را «آزمون نمونه‌های وابسته» (Dependent Sample T-test) نیز نامید. معمولا از این آزمون زمانی استفاده می‌شود که مقدار متغیری قبل و بعد از یک تغییر اندازه‌گیری می‌شود. برای مثال فرض کنید می‌خواهید موثر بودن اثر یک دارو فشار خون را بررسی کنید.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS در فرادرس

کلیک کنید

اگر میزان فشار خون افراد قبل و بعد از مصرف دارو اندازه‌گیری شود، با استفاده از آزمون تی برای مقایسه میانگین زوجی، روش مناسبی برای مشخص کردن اثر بخش بودن دارو است. در چنین وضعیتی می‌خواهیم نشان دهیم که میانگین فشار خون افراد قبل مصرف دارو با میانگین فشار خون بعد از مصرف آن تغییر یا اختلاف معنی‌داری داشته است. در ادامه مثالی برای اجرای آزمون تی توسط کد پایتون ارائه شده است.

مثال

براساس موضوع مصرف دارو و اثر آن بر فشار خون فرضیه‌های به صورت زیر نوشته شده است. نام‌گذاری میانگین برای گروه اول به صورت $$\mu_b$$ در نظر گرفته شده تا بیانگر قبل از مصرف (before) دارو باشد. همچنین میانگین گروه دوم $$\mu_a$$ مشخص شده تا نشانگر میانگین پس از مصرف (after) دارو باشد.

$$\large \begin{cases}H_0: \mu_b =\mu_a \\H_A: \mu_a \neq \mu_b\end{cases}$$

کد زیر برای انجام آزمون مقایسه میانگین فشار خون قبل و بعد از مصرف دارو نوشته شده است. برای دسترسی به اطلاعات مربوطه به این آزمون، فایل اطلاعاتی مورد نظر را از اینجا دریافت کنید.

1import pandas as pd
2from scipy import stats
3df = pd.read_csv("blood_pressure.csv")
4df[['bp_before','bp_after']].describe()
5ttest,pval = stats.ttest_rel(df['bp_before'], df['bp_after'])
6print(pval)
7if pval<0.05:
8    print("reject null hypothesis")
9else:
10    print("accept null hypothesis")

همانطور که دیده می‌شود، تابع stats.ttest_rel برای انجام چنین آزمونی انتخاب شده و مقدار pval یا همان مقدار احتمال، محاسبه و گزارش شده است.

نکته: در اینجا فرض شده است که ستون bp_before مربوط به میزان فشار خون فرد قبل از مصرف دارو است. به این ترتیب مشخص می‌شود که ستون bp_after نیز فشار خون را بعد از مصرف دارو نشان می‌دهد.

آزمون $$Z$$ (Z-test)

در بعضی از مواقع می‌خواهیم آزمون مربوط به میانگین یک جامعه نرمال را با فرض مشخص بودن واریانس جامعه آماری اجرا کنیم. در این حالت استفاده از آماره $$Z$$ (Z Statistics) مناسب‌تر از آماره T‌ است.

آزمون Z تک نمونه‌ای (One Sample Z Test)

در چنین وضعیتی آماره آزمون تک نمونه‌ای به صورت زیر نوشته خواهد شد:

$$\large Z=\dfrac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$$

این آماره دارای توزیع نرمال با میانگین صفر و واریانس ۱ است. بنابراین برای محاسبه مقدار احتمال باید به جداول توزیع نرمال استاندارد مراجعه کرد. در صورتی که شرط‌های زیر برقرار باشد، می‌توان از آماره Z و آزمون Z به جای آزمون T استفاده کرد. مشخص است که در این صورت توان آزمون Z بیشتر از توان آزمون T خواهد بود.

• اندازه یا حجم نمونه بزرگ باشد. اگر تعداد نمونه‌ها بیشتر از ۳۰ باشند می‌توان به جای آزمون T از آزمون Z استفاده کرد.
• نمونه‌های مستقل از یکدیگر باشند. به این معنی که مشاهده یک مقدار در نمونه تصادفی در مقدار مشاهده دیگر تاثیر گذار نباشد.
• توزیع داده‌ها باید نرمال یا حداقل دارای چولگی کم باشد. هر چند برای اندازه نمونه‌های بزرگ انحراف از توزیع نرمال مشکلی ایجاد نمی‌کند.
• نمونه باید به صورت تصادفی تهیه شده باشد و بخصوص در آزمون‌های زوجی، تعداد مشاهدات در هر نمونه یکسان باشد.

در ادامه به بررسی یک مثال در این زمینه می‌پردازیم

مثال

فرض کنید برای آزمودن برابری میانگین فشار خون بیمارانی که دارو مصرف نکرده‌اند با مقدار حدسی برای میانگین (یعنی 156) داده‌هایی جمع‌آوری شده است. این اطلاعات در فایلی که در مثال قبلی مورد بررسی قرار گرفت وجود دارد. کدی که در زیر قابل مشاهده است به این منظور تهیه شده است.

1import pandas as pd
2from scipy import stats
3from statsmodels.stats import weightstats as stests
4ztest ,pval = stests.ztest(df['bp_before'], x2=None, value=156)
5print(float(pval))
6if pval<0.05:
7    print("reject null hypothesis")
8else:
9    print("accept null hypothesis")

همانطور که مشاهده می‌کنید، کد $$stests.ztest(df['bp_before'], x2=None, value=156 )$$ با پارامتر value=156 مشخص می‌کند که مقایسه با میانگین حدسی صورت گرفته است.

آزمون Z دو نمونه‌ای مستقل (Two Sample Z Test)

با فرض نرمال و مشخص بودن واریانس دو جامعه می‌توان به جای آماره T از آماره‌ Z با توزیع نرمال استاندارد استفاده کرد. در چنین حالتی آماره آزمون به صورت زیر نوشته خواهد شد.

$$\large Z=\dfrac{(\overline{X_1}-\overline{X_2})-(\mu_1-\mu_2)}{\sqrt{\sigma^2_1+\sigma^2_2}}$$

مشخص است که این آماره دارای توزیع نرمال استاندارد است و باید مقدار احتمال را بر اساس این توزیع محاسبه کرد. با توجه به مثال مربوط به فشار خون و فرض اینکه داده‌های از جامعه نرمال گرفته شده‌اند، از کد زیر برای انجام آزمون Z دو نمونه‌ مستقل استفاده خواهیم کرد.

1ztest ,pval1 = stests.ztest(df['bp_before'], x2=df['bp_after'], value=0,alternative='two-sided')
2print(float(pval1))
3if pval<0.05:
4    print("reject null hypothesis")
5else:
6    print("accept null hypothesis")

آزمون تحلیل واریانس (ANOVA)

به منظور مقایسه میانگین بین چند جامعه مستقل از روش و آزمون تحلیل واریانس استفاده می‌شود. هر چند به نظر می‌رسد این تحلیل مربوط به واریانس است ولی یکی از کاربردهای آن تحلیل و تشخیص اختلاف بین میانگین چند جامعه است. البته ممکن است مقایسه بین میانگین‌ها را به واسطه آزمون T روی گروه‌های دوتایی از جامعه‌ها نیز انجام داد ولی مشکلی که پیش خواهد آمد افزایش تعداد آزمون‌ها و همچنین افزایش خطای کلی برای آن‌ها است. بنابراین تحلیل واریانس، روشی است که مقایسه بین میانگین چند جامعه مستقل را امکان‌پذیر کرده و خطای مشخص و ثابتی را نیز پوشش می‌دهد.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

اساس آزمون تحلیل واریانس، تجزیه واریانس به دو بخش واریانس یا «پراکندگی بین گروهی» (Between Group Variability) و واریانس یا «پراکندگی درون گروهی» (Within Group Variability) است. نسبت این دو بخش از پراکندگی، آماره‌ای با توزیع F را تشکیل می‌دهد که در آزمون تحلیل واریانس به عنوان آماره آزمون در نظر گرفته می‌شود.

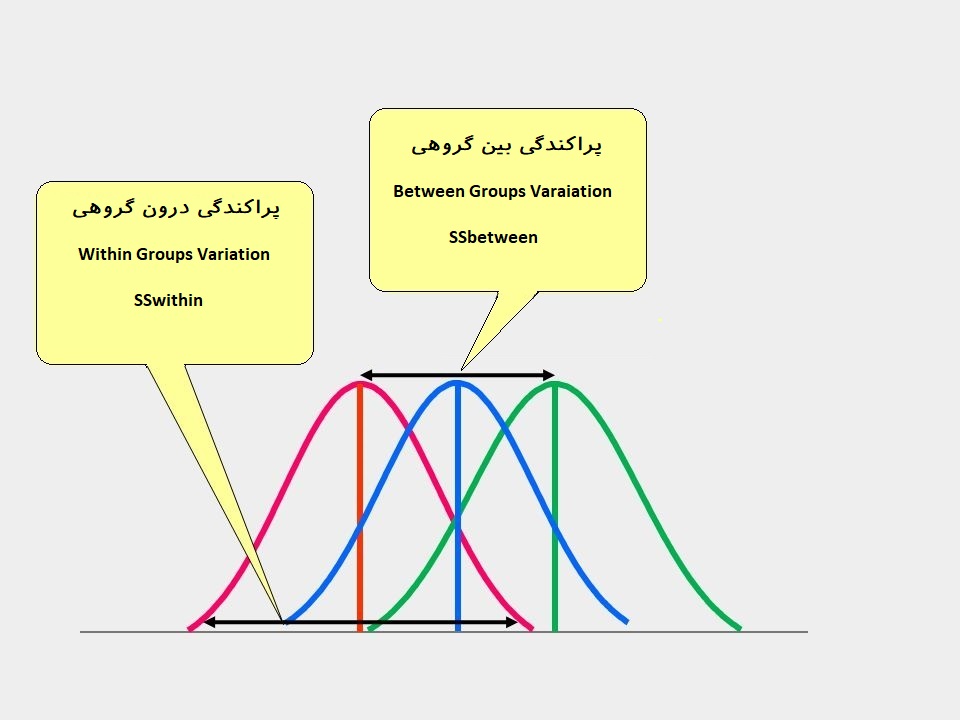
از آنجایی که این پراکندگی‌ها به صورت مربع فاصله‌ها اندازه‌گیری می‌شوند، آماره F دارای مقدارهای مثبت است. حال به شیوه استفاده از آزمون تحلیل واریانس می‌پردازیم.

تحلیل واریانس یک طرفه (One Way ANOVA, F-test)

اگر مقایسه بین دو یا چند جامعه صورت بگیرید و جامعه‌ها توسط سطوح مختلف یک متغیر طبقه‌ای (عامل) ایجاد شده باشند، استفاده از تحلیل واریانس یک طرفه مناسب است. البته در چنین مواقعی ثابت بودن واریانس در بین گروه‌ها از شرط‌های اولیه چنین تحلیلی است. به یاد داشته باشید که در این تحلیل به دنبال مقایسه میانگین در بین چند جامعه هستیم ولی برای انجام آزمون از واریانس‌ها استفاده خواهیم کرد.

مثال

فرض کنید که در یک باغ، سه گونه درخت سیب وجود دارد. از هر گونه نیز به تعداد مشخصی درخت کاشته شده است. در طی ۵ سال، میزان برداشت از این سه گونه درخت ثبت شده است. می‌خواهیم مشخص کنیم که میزان برداشت از این سه گونه یکسان است یا اختلاف در میزان برداشت در این سه گونه وجود دارد. به معنی دیگر می‌خواهیم نشان دهیم که انتخاب صحیح گونه درخت سیب در میزان محصول تاثیر گذار است. داده‌های مربوط به این مثال را می‌توانید از اینجا دریافت کنید. کد زیر به منظور اجرای تحلیل واریانس یک طرفه روی فایل اطلاعاتی به نام PlantGrowth نوشته شده است.

1df_anova = pd.read_csv('PlantGrowth.csv')
2df_anova = df_anova[['weight','group']]
3grps = pd.unique(df_anova.group.values)
4d_data = {grp:df_anova['weight'][df_anova.group == grp] for grp in grps}
5 
6F, p = stats.f_oneway(d_data['ctrl'], d_data['trt1'], d_data['trt2'])
7print("p-value for significance is: ", p)
8if p<0.05:
9    print("reject null hypothesis")
10else:
11    print("accept null hypothesis")

همانطور که دیده می‌شود، تابع stats.f_oneway برای محاسبات تحلیل واریانس استفاده شده است. گروه‌ها یا سه گونه درخت نیز با اسامی ctrl، trt1 و trt2 مشخص شده‌اند. در اینجا عبارتctrl مخفف گروه کنترل (Control) و trt نیز  مخفف تیمار (Treatment) است. به این ترتیب یک گونه به عنوان گروه کنترل و دو گونه دیگر به عنوان تیمار ۱ و تیمار ۲ مشخص شده‌اند.

تحلیل واریانس دو طرفه (Two Way ANOVA, F-test)

برای آزمون برابری میانگین بین چند جامعه که توسط بیش از دو متغیر طبقه‌ای معرفی شوند، باید از تحلیل واریانس دو طرفه استفاده کرد. فرض کنید متغیر طبقه‌ای اول با نام A با دو سطح و متغیر طبقه‌ای دوم نیز با نام B با ۲ سطح جامعه را تقسیم‌بندی کرده باشند. در این صورت با استفاده از آنالیز واریانس دو طرفه می‌توان موارد زیر را مورد بررسی قرار داد.

• متغیر A در تغییر میانگین جامعه‌ها موثر است.
• متغیر B در تغییر میانگین جامعه‌ها موثر است.
• متغیرهای A و B بطور همزمان روی میانگین جامعه‌ها تاثیر گذار هستند.

نکته: البته ممکن است سطوح مختلف برای هر متغیر بیش از ۲ وضعیت باشد. وجود سطوح متعدد در آزمون آنالیز واریانس دو طرفه، پیچیدگی مدل را به همراه خواهد داشت.

در ادامه به بررسی یک مثال در این زمینه پرداخته‌ایم. با اجرای این مثال بیشتر از نحوه انجام این آزمون مطلع خواهید شد.

مثال

فرض کنید دو نوع کود و دو شیوه آبیاری برای درختان یک باغ استفاده شده است. مشخص است که نوع کود می‌تواند به صورت یک متغیر طبقه‌ای (عامل) بر روی میزان محصول اثر گذار باشد. از طرف دیگر، نوع آبیاری نیز آن هم یک نوع متغیر طبقه‌ای محسوب می‌شود، در وزن محصولات درختان تاثیر گذار است. می‌خواهیم اثر هر یک از عوامل و البته اثر متقابل هر دو عامل را روی میانگین محصول بسنجیم. برای انجام این کار به طور تصادفی خاک بعضی از درختان را با کود نوع A و بعضی دیگر را با کود نوع B مخلوط کرده‌ایم. همچنین برای آبیاری نیز به طور تصادفی بعضی از درختان را انتخاب کرده و با شیوه قطره‌ای و بعضی دیگر را به صورت غرقابی آبیاری کرده‌ایم.

کد زیر به منظور انجام آزمون واریانس دو طرفه بر اساس داده‌هایی که از اینجا قابل دریافت هستند، تهیه شده است.

1import statsmodels.api as sm
2from statsmodels.formula.api import ols
3df_anova2 = pd.read_csv("crop.csv")
4model = ols('Yield ~ C(Fert)*C(Water)', df_anova2).fit()
5print(f"Overall model F({model.df_model: .0f},{model.df_resid: .0f}) = {model.fvalue: .3f}, p = {model.f_pvalue: .4f}")
6res = sm.stats.anova_lm(model, typ= 2)
7res

همانطور که دیده می‌شود در قسمتی از  کد که در ادامه مشخص شده است، بین متغیرهای طبقه‌ای از علامت ضرب (*) استفاده شده است. این امر بیانگر محاسبه اثرات اصلی و متقابل هر دو متغیر روی میزان محصول است.

model = ols('Yield ~ C(Fert)*C(Water)', df_anova2).fit()

آزمون کای ۲ (Chi Square Test)

برعکس آزمون‌های t که پارامتری است و با توجه به توزیع داده‌ها صورت می‌گیرد، «ازمون کای ۲» (Chi Sqaure Test) از نوع آزمون‌های ناپارامتری است. به این معنی که برای داده‌ها یا جامعه آماری هیچ توزیعی احتمالی در نظر گرفته نمی‌شود. از این آزمون برای تعیین ارتباط بین دو متغیر طبقه‌ای استفاده می‌شود. برای استفاده از آزمون کای ۲ از یک جدول توافقی که دارای s سطر و r ستون است استفاده می‌شود. سطر‌ها می‌تواند مربوط به سطوح متغیر طبقه‌ای اول و ستون‌ها نیز مربوط به سطوح متغیر طبقه‌ای دوم باشد. آماره مربوط به این آزمون به صورت زیر خواهد بود:

$$V=\sum_{i1=}^s \sum_{j=1}^r \dfrac{(o_{ij}-e_{ij})^2}{e_{ij}}$$

مقدار مورد انتظار با توجه به شرط استقلال دو متغیر طبقه‌ای برای سطر iام و ستون jام با $$e_{ij}$$ نشان داده می‌شود. همچنین مقدارهای مشاهده شده در جدول توافقی در سطرiام و ستون jام به صورت $$o_{ij}$$ مشخص می‌شود. به این ترتیب آماره آزمون V دارای توزیع کای ۲ با $$(s-1)(r-1)$$‌ درجه آزادی است. در ادامه به بررسی یک مثال در این زمینه می‌پردازیم.

مثال

فرض کنید در یک بررسی بازاریابی، خریداران به دو دسته زن و مرد تقسیم شده‌اند. از طرفی طبقه پرسشنامه‌های جمع‌آوری ، علاقه آن‌ها به خرید کالاهای دست دوم پرسیده شده است. با استفاده از جدول توافقی و آزمون استقلال کای ۲ می‌خواهیم بدانیم آیا جنسبت در انتخاب یا خرید کالای دست دوم دخیل است یا خیر. داده‌های مربوط به این آزمون را می‌توانید از اینجا دریافت کنید. مشخص است که در اینجا از دو متغیر طبقه‌ای (جنسیت و علاقمندی)  استفاده شده است. می‌خواهیم نقش هر یک را بر دیگری در آزمون کای ۲ که عمل سنجش استقلال دو متغیر را صورت می‌دهد، مشخص کنیم.

کدی که در ادامه قابل مشاهده است، به این منظور تهیه شده است. همانطور که می‌بینید ابتدا یک جدول توافقی با تابع pd.crosstab ایجاد شده و نتایج حاصل از این جدول برای انجام آزمون به کار گرفته شده است. مقدارهای مورد انتظار در متغیر Expected_Values و مقدارهای مشاهده شده نیز در متغیر Observed_Values ثبت شده‌اند. به این ترتیب آماره آزمون نیز  در متغیر chi_sqaure_statistic محاسبه و ثبت شده است. توجه داشته باشید که درجه آزادی آماره کای ۲ در کد مورد نظر به صورت $$ddof=(no\_of\_rows-1)*(no\_of\_columns-1)$$ بدست آمده است.

1df_chi = pd.read_csv('chi-test.csv')
2contingency_table=pd.crosstab(df_chi["Gender"],df_chi["Shopping?"])
3print('contingency_table :-\n',contingency_table)
4#Observed Values
5Observed_Values = contingency_table.values 
6print("Observed Values :-\n",Observed_Values)
7b=stats.chi2_contingency(contingency_table)
8Expected_Values = b[3]
9print("Expected Values :-\n",Expected_Values)
10no_of_rows=len(contingency_table.iloc[0:2,0])
11no_of_columns=len(contingency_table.iloc[0,0:2])
12ddof=(no_of_rows-1)*(no_of_columns-1)
13print("Degree of Freedom:-",ddof)
14alpha = 0.05
15from scipy.stats import chi2
16chi_square=sum([(o-e)**2./e for o,e in zip(Observed_Values,Expected_Values)])
17chi_square_statistic=chi_square[0]+chi_square[1]
18print("chi-square statistic:-",chi_square_statistic)
19critical_value=chi2.ppf(q=1-alpha,df=ddof)
20print('critical_value:',critical_value)
21#p-value
22p_value=1-chi2.cdf(x=chi_square_statistic,df=ddof)
23print('p-value:',p_value)
24print('Significance level: ',alpha)
25print('Degree of Freedom: ',ddof)
26print('chi-square statistic:',chi_square_statistic)
27print('critical_value:',critical_value)
28print('p-value:',p_value)
29if chi_square_statistic>=critical_value:
30    print("Reject H0,There is a relationship between 2 categorical variables")
31else:
32    print("Retain H0,There is no relationship between 2 categorical variables")
33    
34if p_value<=alpha:
35    print("Reject H0,There is a relationship between 2 categorical variables")
36else:
37    print("Retain H0,There is no relationship between 2 categorical variables")

خلاصه و جمع‌بندی

در قسمت اول از این نوشتار به معرفی مشخصه‌ها و اصطلاحات اصلی مرتبط با آزمون آماری پرداختیم. در قسمت دوم از این مطلب نیز با استفاده از زبان برنامه‌نویسی پایتون به انجام آزمون‌های آماری پرداخته شد. همچنین به کمک مثال‌هایی از توابع پایتون برای انجام آزمون آماری استفاده و فرضیه‌های صفر را در بعضی از مواقع با توجه به مقدار احتمال (p-Value) رد کردیم.

اگر مطلب بالا برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های SPSS
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• آموزش آزمون آماری و پی مقدار (p-value)

^^