تفاوت خطا و مقدار باقیمانده در محاسبات آماری — به زبان ساده

در بسیاری از «تحلیل‌های آماری» (Statistical Analysis) بخصوص در زمینه «مدل‌سازی» (Modeling) در «یادگیری ماشین» (Machine Learning) با اصطلاح «خطا» (Error) و «مقدار باقیمانده» (Residual) مواجه می‌شویم. درک درست از مفهوم این اصطلاحات می‌تواند در توصیف مدل ایجاد شده، برای کسانی که به عنوان «تحلیل‌گر داده‌ها» (Data Scientist) مشغول به کار هستند، بسیار مفید باشد. اغلب افرادی که با تجزیه و تحلیل داده‌ها سروکار دارند، ممکن است باقیمانده را با خطا اشتباه بگیرند. هر چند هر دوی این مقدارها تقریبا به یک شیوه تعریف می‌شوند ولی روش استفاده از آن‌ها در حوزه‌های گوناگون، متفاوت است. در این مطلب قصد داریم برای روشن شدن تفاوت بین خطا و مقدار باقیمانده از مثال‌هایی استفاده کنیم تا درک این دو مفهوم برای خوانندگان بیشتر و بهتر حاصل شود.

هنگام مدل‌سازی در تحلیل‌های رگرسیونی بسیار از خطا و باقیمانده صحبت به میان می‌آید. بنابراین در این مطلب هم از تکنیک‌های رگرسیونی برای بیان تفاوت بین خطا و باقیمانده استفاده خواهیم کرد. از آنجایی که برای این منظور باید از روش و تکنیک‌های رگرسیونی آگاه باشید، بهتر است قبلا مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده را مطالعه کرده و یا از قبل اطلاعاتی در این زمینه کسب کنید. از طرفی خواندن تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست زیرا در این تکنیک آماری نیز از مفاهیم خطا و باقیمانده بسیار استفاده می‌شود.

خطا و مقدار باقیمانده

فرض کنید یک سری مشاهدات از متغیرهای تصادفی یک بُعدی از توزیع یکسانی در اختیارتان هست و قرار است میانگین توزیع را به عنوان یک پارامتر جامعه آماری یا توزیع مورد نظر، برآورد کنید. در اصطلاح مدل‌سازی میانگین را گاهی «پارامتر مکان» (Location Parameter) نیز می‌نامند. در چنین وضعیتی «خطا» (Error) فاصله یا انحرافی است که مقدار برآورد شده برای پارامتر مکان از مقدار واقعی آن دارد.

فیلم آموزش تخمین خطای طبقه بندی یا کلاسیفایر در داده کاوی در فرادرس

کلیک کنید

البته براساس توابع فاصله یا شیوه‌های محاسبه انحراف، ممکن است این مقدار به صورت‌های متفاوتی بدست آید. ولی نکته مهم در این است که اگر مقدار واقعی پارامتر توزیع مشخص نباشد، نمی‌توان خطای برآورد را محاسبه کرد. در ادامه علت این امر مشخص خواهد شد.

به این ترتیب با توجه به توضیحات بالا می‌توان این وضعیت را برای توزیع نرمال یک متغیره در نظر گرفت. فرض کنید $$X_1, \dots, X_n\sim N(\mu,\sigma^2)$$ نمونه تصادفی $$n$$ تایی iid از جامعه نرمال باشند. واضح است که پارامترهای این توزیع به ترتیب میانگین ($$\mu$$) و واریانس ($$\sigma^2$$) هستند. به این ترتیب خطا آماری به صورت زیر محاسبه می‌شود.

$$\large E_{i}=X_{i}-\mu ,\,$$

واضح است که در این حالت با فرض اینکه هنوز مشاهده‌ای برای $$X_i$$ وجود ندارد، خطای $$E_i$$ نیز یک متغیر تصادفی است که توزیعی مشابه با توزیع $$X_i$$ دارد. در صورتی که مقادیر متغیر تصادفی مشاهده شود و پارامتر توزیع نیز معلوم باشد، می‌توان خطاها را به ازاء هر مشاهده، به شکل زیر محاسبه کرد.

$$\large \operatorname{e}_{i}=x_{i}-\mu ,\,$$

در نتیجه میانگین خطا به صورت زیر در خواهد آمد.

$$\large \overline{\operatorname{e}}=\overline{x}-\mu ,\,$$

برای مثال فرض کنید متوسط سن دانشجویان در یک دانشگاه (جامعه آماری) برابر با ۲۱ سال است. یک دانشجو به تصادف انتخاب شده و سنش مورد پرسش قرار گرفته است. به این ترتیب مشخص شده که سن او برابر با ۲۷ سال است. در این حالت مقدار خطا سن این فرد از میانگین سن دانشجویان (میانگین جامعه آماری) برابر با $$27-21=6$$ است.

اگر هدف از انجام بررسی آماری محاسبه مجموع مربعات خطا باشد (مانند روش تحلیل واریانس) می‌دانیم که توزیع آماری این شاخص مرتبط با توزیع کای ۲ با $$n$$ درجه آزادی است. به این ترتیب خواهیم داشت:

$$\large {\frac 1{\sigma ^{2}}}\sum _{{i=1}}^{n}e_{i}^{2}\sim \chi _{n}^{2}$$

نکته: همانطور که مشاهده شده، خطای آماری ($$E$$) یک متغیر تصادفی است در حالیکه مقدار خطای آماری ($$\operatorname{e}$$) براساس مقادیر مشاهده شده از متغیرهای تصادفی حاصل می‌شود.

در مقابل باقیمانده یا مقدار «اختلاف برازش» (Fitting Deviation)، مقداری است که براساس برآورد میزان خطای آماری حاصل می‌شود. فرض کنید به کمک روش‌های برآوردیابی مثلا روش حداکثر درستنمایی (با فرض معلوم بودن واریانس) می‌دانیم که برآوردگر مناسب برای میانگین جامعه نرمال، میانگین نمونه ($$\overline{X}$$) است.

$$\large \overline{X}={X_1 + \cdots + X_n \over n}$$

در این حالت باقیمانده با $$r_i$$ نشان داده شده و به صورت زیر محاسبه می‌شود.

$$\large r_{i}=X_{i}-\overline {X}$$

از آنجایی که می‌دانیم $$X_i$$ها متغیر تصادفی هستند، باقیمانده $$r_i$$ نیز متغیر تصادفی است. به مانند قبل اگر هدف، محاسبه مربعات مقادیر باقیمانده باشد، توزیع آماری آن، کای ۲ با $$n-1$$‌ درجه آزادی خواهد بود. در این صورت رابطه زیر برقرار است.

$$\large {\frac 1{\sigma ^{2}}}\sum _{{i=1}}^{n}r_{i}^{2}\sim \chi _{{n-1}}^{2}$$

توجه داشته باشید که هم در مجموع مربعات خطا و هم در باقیمانده‌ها، فرض بر معلوم بودن واریانس در جامعه آماری است و خطا یا باقیمانده برای میانگین جامعه آماری نسبت به مشاهدات محاسبه شده است. از طرفی تفاوت در توزیع آماری مجموع مربعات خطا و باقیمانده نیز دیده می‌شود بطوری که در اولی درجه آزادی توزیع کای ۲ برابر با $$n$$ و در دومی برابر با $$n-1$$‌ است.

نکته: با توجه به قضیه باسو مشخص است که میانگین نمونه آماری از مجموع مربعات باقیمانده‌ها مستقل است. در نتیجه نسبتی که در رابطه زیر نوشته شده دارای توزیع $$t$$ با $$n-1$$ درجه آزادی خواهد بود. البته باید توجه داشت که منظور از $$S_n$$‌ نیز انحراف استاندارد نمونه‌ای برای $$n$$ نمونه تصادفی است.

$$\large {\displaystyle {\frac {{\overline {X}}_{n}-\mu }{S_{n}/{\sqrt {n}}}}}\sim t_{(n-۱)}$$

خطا و مقدار باقیمانده در رگرسیون

تشخیص تفاوت بین خطا و مقدار باقیمانده در تجزیه و تحلیل رگرسیون مقداری گنگ بوده ولی بسیار مهم است. بر این اساس مفاهیم دیگری مانند باقیمانده‌های Studentized در مقابل باقیمانده‌های Standardized ظاهر می‌شود. اگر در رگرسیون خطی یک تابع به شکل خط با پارامتری نامعلوم بیانگر رابطه بین متغیر مستقل و متغیر وابسته باشد، فاصله یا اختلاف بین مقدارهای واقعی متغیر وابسته و مقدارهای پیش‌بینی شده توسط تابع خطی، خطای غیرقابل مشاهده را مشخص می‌کند، زیرا هنوز پارامترهای مدل خطی برآورد نشده‌اند.\

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

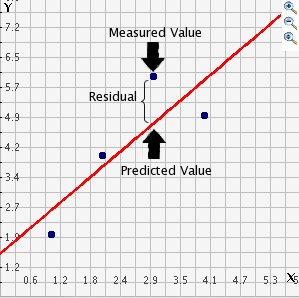
ولی اگر پارامترهای مدل توسط زوج مشاهده‌های مربوط به $$X$$ و $$Y$$ به عنوان متغیرهای مستقل و وابسته برآورد شده باشد، اختلاف بین مقدار واقعی (Measured Value) و مقدار «برازش شده» (Fitted Value) یا «مقدار پیش‌بینی شده» (Predicted Value) توسط مدل (که پارامترهای آن مشخص است)، باقیمانده را تعیین می‌کند.

شاید مفهوم خطا و باقیمانده در تعریف «میانگین مربعات خطا» (Mean Squared Error - MSE) بهتر قابل درک باشد. MSE برای یک مدل رگرسیونی، مقداری است که براساس مجموع مربعات باقیمانده‌ها حاصل می‌شود و ارتباطی با خطاهای غیرقابل مشاهده ندارد. اگر مجموع مربعات باقیمانده‌ها را بر تعدادشان یعنی $$n$$ تقسیم کنیم میانگین مربعات باقیمانده حاصل خواهد شد. در ادامه این رابطه برای متغیر وابسته $$Y$$ محاسبه شده است.

$$\large {\displaystyle \operatorname {MSE_b} ={\frac {1}{n}}\sum _{i=1}^{n}(Y_{i}-{\hat {Y_{i}}})^{2}}$$

از آنجایی که میانگین مربعات باقیمانده ارائه شده در رابطه بالا، برآوردگر «اریب» (Biased) برای واریانس خطا محسوب می‌شود آن را به صورت $$MSE_b$$ نشان داده‌ایم. با تقسیم مجموع مربعات باقیمانده‌ها بر $$df=n-p-1$$ برآوردگر نااریب واریانس خطا بدست خواهد آمد. واضح است که در اینجا $$p$$ تعداد پارامترهای برآورد شده و $$df$$ درجه آزادی برای مجموع مربعات باقیمانده‌ها در نظر گرفته‌ شده است. این «آماره» (Statistic) که به عنوان برآوردگر نااریب واریانس خطاهای غیرقابل مشاهده در نظر گرفته می‌شود مطابق با رابطه زیر محاسبه می‌شود.

$$\large {\displaystyle \operatorname {MSE} =\frac {1}{n-p-1}\sum _{i=1}^{n}(y_{i}-{\hat {y_i}})^2}$$

یکی دیگر از روش‌های آماری که وابسته به خطا و باقیمانده است، تکنیک «تحلیل واریانس» یا (ANOVA (Analysis of Variance در تحلیل رگرسیونی است. به این ترتیب براساس تجزیه «مجموع مربعات کل خطا» مشاهدات (Total Sum of Squared) مربوط به متغیر وابسته به مجموع «مربعات خطای رگرسیون» (Sum of Squared- Regression) و «مجموع مربعات خطا» (Sum of Squared Error)، می‌توان نسبت به وجود اختلاف در میانگین‌های چند جامعه آماری رای داد. به این ترتیب با استفاده از آماره‌ای با توزیع $$F$$، آزمون فرض آماری نسبت به یکسان یا وجود اختلاف در میانگین جوامع، صورت می‌گیرد. با مشاهده مقادیر و محاسبه مقدارهای برازش شده،‌ خطاها تبدیل به باقیمانده شده و مقدار آماره آزمون با مقدار $$F$$ توزیع مقایسه می‌شود. به این ترتیب ملاکی برای رد یا عدم رد فرض صفر بوجود می‌آید.

از طرف دیگر، در مدل رگرسیونی فرض بر این است که باقیمانده‌ها دارای توزیع یکسان بوده و نسبت به هم مستقل هستند. البته در رگرسیون خطی OLS، فرض نرمال بودن برای خطاها نیز وجود دارد. هر چند در روند انجام تحلیل رگرسیونی، توزیع باقیمانده‌ها برای همه نقاط یکسان در نظر گرفته می‌شود ولی به علت اینکه مقدارهایی که دور از مرکز یا میانگین متغیر مستقل قرار گرفته‌اند، نقش بیشتری در کمینه‌سازی تابع هدف (کمینه‌سازی مربعات خطا) دارند، بهتر توسط مدل رگرسیونی برازش می‌شوند، به معنی دیگر این نقاط دارای خطای کمتری هستند.

به این ترتیب برای مقایسه باقیمانده‌ها در نقاط مختلف متغیر مستقل، باید باقیمانده به شکلی استاندارد شود. این شیوه به نام Studentizing مشهور است. این کار یعنی Studentized‌ کردن باقیمانده‌ها، به شناسایی «نقاط پرت» (Outlier) کمک می‌کند.

باقیمانده‌های Studentized

فرض کنید یک مدل رگرسیونی خطی ساده بین متغیر مستقل $$X$$ و وابسته $$Y$$ به صورت زیر ایجاد شده است.

$$\large Y = \alpha_0 + \alpha_1 X + \varepsilon$$

به این ترتیب مشخص است که برای زوج $$(X_i,Y_i)$$ رابطه زیر برقرار است.

$$\large Y_i = \alpha_0 + \alpha_1 X_i + \varepsilon_i,\;\;\;i=1,2,\ldots,n$$

از طرفی مشخص است که در رابطه بالا منظور از $$\varepsilon_i$$ خطای مربوط به مدل در نقطه $$X_i$$ است. فرض بر این است که این خطاها مستقل و همتوزیع با واریانس ثابت $$\sigma^2$$ در نظر گرفته شده است. اما برآورد این خطا که همان باقیمانده‌ها هستند براساس مقدارهای مشاهده شده برای متغیرهای مستقل $$X$$ و وابسته $$Y$$ بدست می‌آیند و به نظر می‌رسد دیگر مستقل از یکدیگر نیستند زیرا در روش OLS شرط‌های زیر را باید برایشان در نظر گرفته باشیم.

$$\large {\displaystyle \sum _{i=1}^{n}{\widehat {\varepsilon \,}}_{i}=0}$$

$$\large {\displaystyle \sum _{i=1}^{n}{\widehat {\varepsilon \,}}_{i}x_{i}=0}$$

در رابطه‌های بالا منظور از $$\widehat {\varepsilon_i}$$ باقیمانده مشاهده $$i$$ام است.

متاسفانه باقیمانده‌ها برعکس خطاها دارای واریانس ثابت و یکسانی نیستند. واریانس باقیمانده‌ها، زمانی که مقدارهای متغیر مستقل $$x$$ از میانگینشان دور می‌شود، کاهش یافته و زمانی که به میانگین نزدیک می‌شود، افزایش می‌یابد. این تغییرات در «تابع اثر» (Influence Function) نیز به خوبی دیده می‌شود. به این ترتیب برای نشان دادن صحت شرایط مدل رگرسیونی بهتر است به جای مقایسه باقیمانده‌های استاندارد شده (Standardized) از باقیمانده‌های Studentized استفاده شود.

فرض کنید ماتریس طرح مدل رگرسیونی را به صورت زیر در نظر گرفته‌ایم.

$$\large X=\left[\begin{matrix}1 & x_1 \\ \large \vdots & \vdots \\ \large 1 & x_n \end{matrix}\right]$$

به این ترتیب ماتریس تصویر عمودی برای ماتریس طرح (Hat Matrix) را به صورت زیر خواهیم داشت.

$$\large H=X(X^T X)^{-1}X^T$$

این ماتریس عمل برآورد را روی متغیر $$X$$ انجام می‌دهد. به این معنی که مقدار برازش شده برای بردار $$Y$$ به شکل زیر حاصل می‌شود.

$$\large {\displaystyle {\widehat {y }}=X {\widehat {\boldsymbol {\beta }}}=X \left(X ^TX \right)^{-1}X ^Ty}=Hy$$

همچنین در نظر داشته باشید که واریانس خطای مدل رگرسیونی $$\sigma^2$$ را به صورت زیر برآورد کرده‌ایم:

$$\large{\displaystyle {\widehat {\sigma }}^{2}={1 \over n-p}\sum _{i=1}^{n}{\widehat {\varepsilon \,}}_{i}^{\,2}}$$

به این ترتیب باقیمانده Studentized شده مطابق با رابطه زیر قابل محاسبه است.

$$\large{\displaystyle t_{i}={{\widehat {\varepsilon \,}}_{i} \over {\widehat {\sigma }}{\sqrt {1-h_{ii}\ }}}}$$

که در آن $$h_{ii}$$‌ مولفه‌های روی قطر اصلی (سطر $$i$$ام و ستون $$i$$ام) ماتریس $$H$$ هستند. به این ترتیب $$t_i$$ها دارای توزیع مشابه توزیع $$t$$‌ هستند. یعنی داریم:

$$\large t_{i}\sim {\sqrt {n-p }}{t \over {\sqrt {t^{2}+n-p -1}}}$$

که در آن $$t$$ دارای توزیع student't با $$n-p-1$$‌ درجه آزادی است.

خلاصه

همانطور که دیدید، خطا در مباحث آماری به عنوان یک متغیر تصادفی در نظر گرفته شده که وابسته به پارامتر توزیع جامعه آماری است. ولی از طرف دیگر باقیمانده به میزان خطای قابل اندازه‌گیری گفته می‌شود که وابسته به برآوردهای حاصل از پارامتر جامعه است. هر چند هر دو مفهوم برای مشخص کردن میزان انحراف به کار گرفته می‌شوند ولی توزیع‌های آماری و زمینه استفاده از آن‌ها با یکدیگر متفاوت است.

فیلم آموزش مدیریت خطا و حالات استثنایی برنامه ها در متلب (رایگان) در فرادرس

کلیک کنید

در مطالب مربوط به مباحث آماری در اکثر اوقات فاصله یا انحراف را به صورت مربع تفاضل مقدار مشاهده شده از مقدار مورد انتظار در نظر می‌گیرند. در حقیقت مربع فاصله اقلیدسی ملاک محاسبه خطا یا انحراف است و به این ترتیب جهت اختلاف را از بین می‌برند. ولی ممکن است برای از بین بردن جهت اختلاف از روش‌ها یا توابع دیگری نیز استفاده شود. برای مثال از توابع فاصله مانند «فاصله ماهالانوبیس» (Mahalanobis Distance) یا «فاصله منهتن» (Manhattan Distance) نیز در بسیاری از تکنیک‌های آماری استفاده شده و مبنای اندازه‌گیری اختلاف یا خطا را این توابع در نظر می‌گیرند.به عنوان نمونه، در شیوه محاسبه میانگین قدر مطلق انحرافات از میانه (Median Absolute Deviation) از فاصله منهتن استفاده شده است.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• مجموعه آموزش‌های مدل سازی، برازش و تخمین
• رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده
• هم خطی در مدل رگرسیونی — به زبان ساده

^^