القای الکترومغناطیسی (Electromagnetic Induction) — از صفر تا صد

پیش‌تر در بلاگ فرادرس در مورد مفاهیم میدان مغناطیسی و قانون القای فارادی صحبت شد. در مطالب مذکور عنوان شد که اگر میدان مغناطیسی عبوری از یک حلقه رسانای بسته، با زمان تغییر کند، جریانی الکتریکی در آن حلقه القا خواهد شد. مفاهیم القا (Inductance) و انرژی مغناطیسی، بیان می‌کنند که چگونه یک جریان الکتریکی می‌تواند عامل ایجاد جریان در رسانای دومی شود.

پیشنهاد می‌شود قبل از مطالعه این مطلب، قانون دست راست را نیز مطالعه فرمایید.

القای متقابل

مطابق با شکل زیر دو سلونوئید را در نظر بگیرید که کنار هم قرار گرفته‌اند.

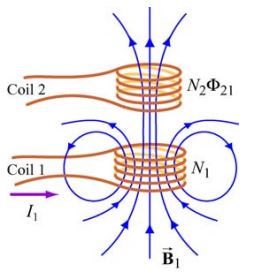
تعداد حلقه‌ها و جریان سلو‌نوئید اول به‌ترتیب برابر با N₁ و I₁ است که منجر به تولید میدان مغناطیسی $$\large {\overrightarrow{B}_{1}}$$ می‌شود. زمانی که دو سلونوئید به یکدیگر نزدیک شوند، تعدادی از خطوط میدان مغناطیسیِ سلونوئید اول از سلونوئید دوم نیز عبور خواهند کرد. فرض کنید Φ_۲۱، نشان دهنده شار مغناطیسی عبوری از یک حلقه‌ی سلونوئید دوم، ناشی از جریان I₁ باشد. حال با تغییر جریان I₁ با زمان، نیروی محرکه القایی بوجود خواهد آمد که ناشی از تغییر شار مغناطیسی عبوری از سلونوئید دوم است. این نیروی محرکه برابر است با:

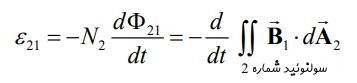
در حقیقت تغییر شار مغناطیسی Φ_۲۱ در سلونوئید شماره ۲، متناسب با تغییر زمانی جریان در سلونوئید شماره ۱ است. از این رو می‌توان گفت:

در رابطه بالا M₂₁ ضریب القای متقابل است و می‌توان آن را در قالب رابطه زیر نشان داد:

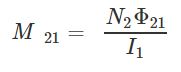
واحد SI خودالقایی، هانری (H) است. در حقیقت:

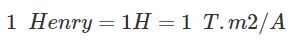
همان‌گونه که در رابطه بالا نیز دیده می‌شود، ضریب خودالقایی M₂₁ به شکل هندسی دو سلونوئید و تعداد حلقه‌های آن‌ها وابسته است. به طریقی مشابه فرض کنید جریان I₂ در سلونوئید دوم برقرار است و با زمان تغییر می‌کند. در نتیجه نیرو محرکه در سلونوئید شماره ۱ برابر می‌شود با:

مطابق با شکل زیر نیروی محرکه بدست آمده در بالا منجر به ایجاد جریان در سولنوئید شماره ۱ نیز می‌شود.

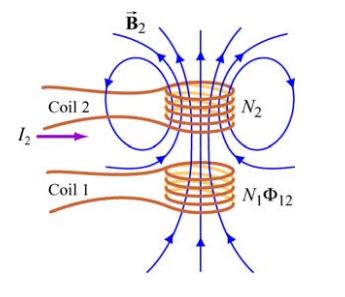
تغییر شار مغناطیسی عبوری از سلونوئید شماره ۱ متناسب با تغییرات زمانی جریانِ سلونوئید شماره ۲ است. بنابراین داریم:

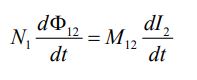
در رابطه بالا M_۱۲ نیز ضریب القای متقابل است که می‌توان آن را به‌شکل زیر بدست آورد.

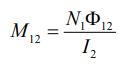
با استفاده از قانون متقابل، که در نتیجه ترکیب قوانین آمپر و بیو-ساوار است، رابطه بین ضرایب خودالقایی برابر است با:

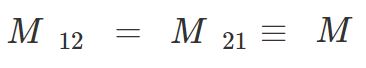
رابطه بالا نشان می‌دهد که ضریب القای متقابل در هر دو سناریو برابر هستند. جهت درک بهتر مفاهیم بالا توجه شما را به مثالی که در ادامه آمده جلب می‌کنیم.

مثال ۱: القای متقابل دو حلقه هم‌مرکز

مطابق با شکل زیر دو حلقه بسته به شعاع‌های R₁ و R₂ را در نظر بگیرید.

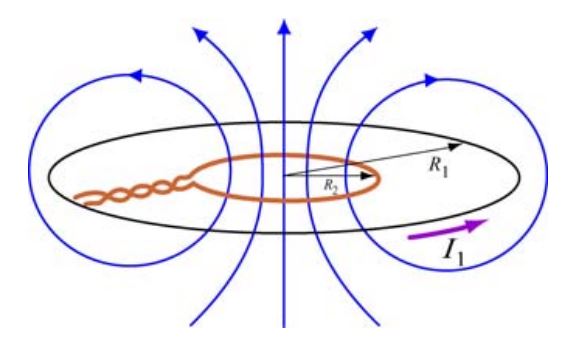
القای متقابل این دو حلقه چقدر است؟

در ابتدا بایستی میدان مغناطیسی در مرکز حلقه و ناشی از جریان I₁ را بیابیم. در نتیجه اندازه میدان مذکور برابر است با:

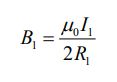
با توجه به این‌که R₁>>R₂ است، در نتیجه میدان مغناطیسی در تمامی فضای حلقه کوچک‌تر (حلقه شماره ۲) را می‌توان برابر با B₁ فرض کرد. بنابراین شار عبوری از حلقه مذکور برابر است با:

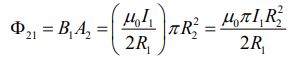
از این رو ضریب القای متقابل برابر است با:

توجه داشته باشید که اگر با استفاده از شار عبوری از حلقه شماره ۱، ناشی از حلقه شماره ۲ نیز مسئله را حل می‌کردیم، به همین نتیجه می‌رسیدیم. دلیل استفاده از این روش، یکنواخت فرض شدن میدان مغناطیسی در حلقه شماره ۲ است که باعث می‌شود مسئله راحت‌تر حل شود.

رابطه بالا از این زاویه جالب است که ضریب القای متقابل تنها به پارامتر‌های هندسی، هم‌چون R₁ و R₂ وابسته است و به جریان‌های دو سیم‌پیچ (همان سولنوئید) وابسته نیست.

خودالقایی

مطابق شکل زیر سلونوئیدی با N حلقه را در نظر بگیرید که جریان I را در خود و در جهت پادساعتگرد دارد. اگر جریان بصورت پایا باشد، میدان مغناطیسی عبوری از حلقه ثابت خواهد ماند. در حالتی دیگر فرض کنید که جریان I با زمان تغییر کند. در این شرایط،‌ مطابق با قانون القای فارادی،‌ نیروی محرکه القایی، در خلاف جهت تغییرات جریان الکتریکی است. در حقیقت با فرض این‌که dI/dt > 0  باشد، جریان الکتریکی القایی، ساعتگرد و در حالت dI/dt < 0،‌ جریان القاییِ پادساعتگرد در حلقه بوجود خواهد آمد.

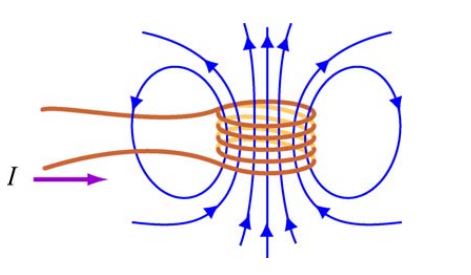
به این خاصیت از حلقه جریان که در آن میدان مغناطیسی القایی، در خلاف جهت تغییرات جریان الکتریکی است، خودالقایی گفته می‌شود. هم‌چنین نیروی محرکه ناشی از تغییر مذکور،‌ نیروی محرکه خود القایی نامیده می‌شود و آن را با $$\epsilon_L \enspace$$ نشان می‌دهند. تمامی حلقه‌های حامل جریان این خاصیت را دارند. به‌طور ویژه، سلونوئید، جزئی از مدار الکتریکی است که دارای ضریب خودالقایی بزرگی است.

نیروی محرکه خود القایی را می‌توان با استفاده از قانون القای فارادی، به شکل زیر بیان کرد:

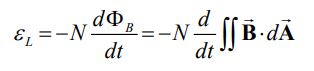
نیروی محرکه بالا را می‌توان با استفاده از مفهوم ضریب ثابت خودالقایی، به شکل زیر بدست آورد:

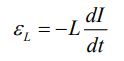
با ترکیب دو رابطه بالا داریم:

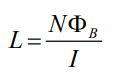
از منظر فیزیکی، ضریب القایی L، میزان مقاومت القاگر در مقابل تغییرات جریان الکتریکی القاگر را نشان می‌دهد. L بزرگ‌تر نشان‌ دهنده تغییرات زمانی کوچک‌تر جریان الکتریکی است.

مثال ۲: خودالقایی سولنوئید

ضریب خودالقایی سولنوئید زیر با N حلقه، طول L، شعاع R و جریان I را بدست آورید.

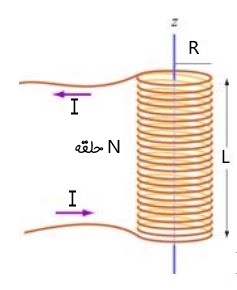
با در نظر نگرفتن اثر لبه و استفاده از قانون آمپر، میدان مغناطیسی در وسط سولنوئید برابر است با:

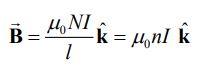
در رابطه بالا n=N/l، نشان دهنده تعداد دور‌های حلقه در واحد طول است. در نتیجه شار مغناطیسی عبوری از هرکدام از این حلقه‌ها برابر است با:

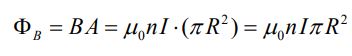
بنابراین ضریب خودالقایی سولنوئید برابر با مقدار زیر بدست می‌آید.

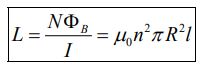
رابطه بالا دوباره بر این موضوع تاکید می‌کند که ضریب خودالقایی تنها به پارامترهای هندسی القاگر وابسته است.

مثال ۳: خودالقایی تروئید (Toroid)

تروئید سیم‌پیچی حلقوی است که نقش القاگر را در مدار‌های الکتریکی ایفا می‌کند. مطابق با شکل زیر تروئیدی را شامل N حلقه در نظر بگیرید که مقطع آن به‌صورت مستطیلی است. فرض کنید ارتفاع، شعاع داخلی و خارجی این سولنوئید به ترتیب برابر با b ,a ,h است.

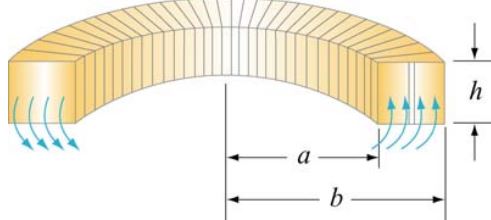
مطابق با قانون آمپر که در بخش قبل در مورد آن بحث شد، میدان مغناطیسی در سلونوئید با استفاده از رابطه زیر بدست می‌آید.

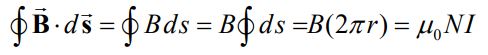
یا

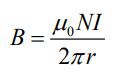
شار مغناطیسی عبوری از یک حلقه تروئید، با انتگرال‌گیری از میدان مغناطیسی روی دیفرانسیل سطح dA=hdr نشان داده شده در شکل زیر بدست می‌آید.

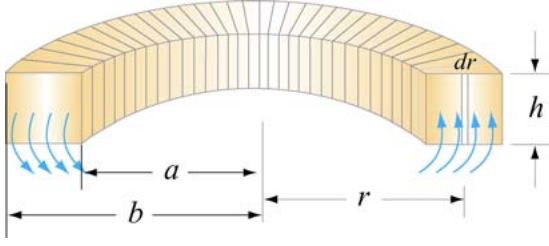
با محاسبه انتگرال میدان مغناطیسی روی سطح دیفرانسیلی نشان داده شده در شکل بالا داریم:

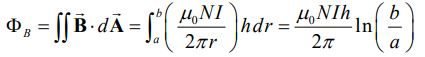
با فرض این‌که شار عبوری از N حلقه برابر با $$N \Phi_B$$ باشد، ضریب خودالقایی برابر می‌شود با:

رابطه بالا نیز نشان می‌دهد که ضریب خودالقایی تنها به ویژگی‌های هندسی القاگر مرتبط است. حال تروئیدی را تصور کنید که در آن a>>b-a است. در حالتی حدی، عبارت لگاریتمیِ رابطه بالا به شکل زیر قابل بازنویسی می‌شود:

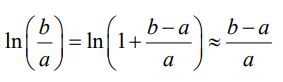
در نتیجه ضریب خودالقایی برابر است با:

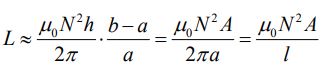
در رابطه بالا (A = h (b-a، مقطع تیروئید و L=2πa محیط داخلی آن است. بنابراین ضریب خودالقایی تروئید در حالت حدی برابر با ضریب سولنوئید شده که نشان دهنده درست بودن حل است.

مثال ۴: سیمِ پیچیده شده دور سولنوئید

همانند تصویر زیر سولنوئیدی به طول l،‌ تع

داد دور سیمِ N₁ و سطح مقطع A را در نظر بگیرید. فرض کنید سیم عایقی با تعداد دورِ N₂ اطراف آن پیچیده شده است.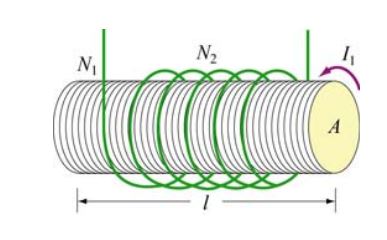

 

1. با توجه به توصیفات بالا، القای متقابل M را با این فرض بیابید که تمامی شار تولید شده توسط سولنوئید از سیم‌ پیچ خارجی عبور می‌کند.
2. رابطه بین M و ضرایب خودالقایی L₁ و L₂ سولنوئید و سیم‌پیچ را بیابید.

(a): شار مغناطیسی تولید شده توسط سولنوئید که از یک حلقه‌ی سیم‌پیچ عبور می‌کند، برابر است با:

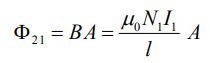
در رابطه بالا $$B \enspace =\mu_0 N_1I_1 /l$$، میدان مغناطیسی یکنواخت تولید شده توسط سولنوئید است. در نتیجه ضریب القایی متقابل برابر است با:

(‌b): با توجه به مثال ۲، ضریب خودالقایی سولنوئیدی با N₁ حلقه، برابر است با:

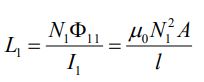
در رابطه بالا $$\Phi_{11}$$ شار مغناطیسی عبوری از یک حلقه‌ی سولنوئید است که توسط جریان I₁ تولید شده. به همین روش ضریب خودالقایی برای سیم‌پیچ بیرونی برابر است با:

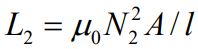
با توجه به روابط ۱، ۲ و ۳ ارتباط بین ضریب القای متقابلِ M و ضرایب خودالقایی L₁ و L₂ برابر است با:

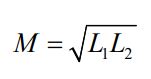
البته رابطه بالا را می‌توان به شکلی عمومی‌تر و به‌صورت زیر بیان کرد:

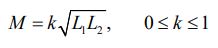
در رابطه بالا k را تحت عنوان «ضریب تزویج» (Coefficient of Coupling) می‌شناسند. این ضریب معیاری از میزان شار مغناطیسی تولید شده توسط سولنوئید است که از سیم‌پیچ عبور می‌کند.

انرژی ذخیره شده در میدان مغناطیسی

از آنجایی که در یک سولنوئید، میدان مغناطیسی تولید شده با جریان حامل در آن مخالفت می‌کند، بنابراین به‌منظور برقراری جریان، بایستی از کار خارجی استفاده شود. کار خارجی می‌تواند باتری یا هر منبع دیگری باشد.

جهت ایجاد جریانِ I در القاگر از توان خارجی $$\epsilon_{ext}$$ استفاده می‌شود. این توان جهت ایجاد جریان I در سولنوئید و مقابله با نیروی محرکه القا شده‌ی $$\epsilon_{L}$$ مورد استفاده قرار می‌گیرد. نیروی محرکه خارجی استفاده شده برابر است با:

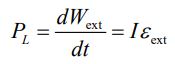
با توجه به این‌که در فرض بالا تنها نیروی محرکه القا شده و نیرو محرکه خارجی وجود دارند، بنابراین می‌توان رابطه $$\epsilon_{L}$$=$$-\epsilon_{ext}$$ را بیان کرد. در نتیجه تعادل انرژی به شکل زیر قابل بازنویسی است:

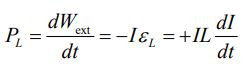
اگر نرخ جریان در زمان افزایشی باشد (dl/dt > 0)، در این صورت p>0 است. این جمله به معنی آن است که نیروی خارجی به سیستم انرژی می‌دهد. بنابراین U_B یا همان انرژی القاگر افزایش می‌یابد. از سویی دیگر اگر جریان الکتریکی با زمان کاهش یابد (dI/dt < 0)، در این صورت توان P نیز منفی است. بنابراین در این حالت منبع خارجی از سیستم انرژی می‌گیرد. در حالتی که منبعی با کار خارجی، جریانی را از صفر تا I افزایش دهد، کار خارجی انجام شده جهت این افزایش جریان، برابر است با:

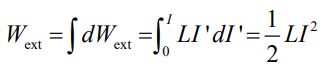
این کار معادل با انرژی ذخیره شده در القاگر است. بنابراین انرژی ذخیره شده در القاگری که جریان آن از صفر تا I افزایش یافته برابر است با:

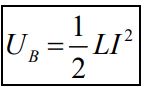
با دقت در رابطه بالا احتمالا متوجه شده‌اید که بسیار شبیه به رابطه میزان انرژی ذخیره شده در خازن است که در زیر بیان شده.

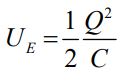
توجه داشته باشید که از منظر انرژی، تفاوت عمده‌ای میان یک القاگر و یک مقاومت وجود دارد. زمانی که جریان I به یک مقاومت وارد می‌شود، انرژی به درون آن جریان یافته و در قالب حرارت خارج می‌شود. این فرآیند ربطی به پایا یا ناپایا بودن جریان ندارد. اما در یک القاگر، تنها زمانی انرژی به آن وارد می‌شود که جریان الکتریکی ناپایا بوده و با زمان افزایش یابد (dI/dt > 0). در این حالت، انرژی به القاگر وارد شده و دفع نمی‌شود. در حقیقت زمانی این انرژی دفع می‌شود که جریان ورودی به القاگر با زمان کاهش یابد (dI/dt < 0). اگر جریان ورودی به القاگر با زمان ثابت باشد، با توجه به رابطه P_L = LI dI/dt انرژی ذخیره شده در آن نیز تغییر نخواهد کرد.

مثال ۵: انرژی ذخیره شده در سولنوئید

سولنوئید طویلی به طول l و شعاع R را در نظر بگیرید که از N حلقه سیم تشکیل شده است. جریانی به اندازه I از آن عبور می‌کند. انرژی ذخیره شده در آن را بیابید.

در ابتدا با استفاده از رابطه انرژی ذخیره شده در سولنوئید، انرژی ذخیره شده در این سولنوئید نیز برابر می‌شود با:

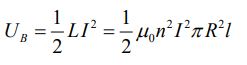
البته رابطه بالا را می‌توان در قالب اندازه میدان مغناطیسی $$B \enspace =\enspace \mu_0nI $$ نیز بیان کرد:

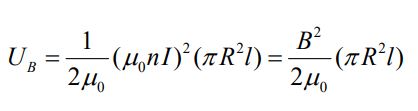
با توجه به این‌که πR²l حجم درون سولنوئید است، در نتیجه با استفاده از چگالی انرژی مغناطیسی بیان شده در زیر، کل انرژی موجود در سولنوئید را می‌توان محاسبه کرد.

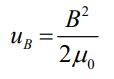
رابطه بالا حتی در حالتی که میدان مغناطیسی یکنواخت نباشد، نیز صادق خواهد بود. مثال بالا انرژی موجود در یک میدان مغناطیسی را محاسبه می‌کند. اما با وجود برقراری جریان الکتریکی در القاگر، تغییر این انرژی با زمان صفر است. برای درک بهتر تصور کنید که جریان I از یک مقاومت الکتریکی عبور کند؛ در این حالت انرژی تلف شده توسط مقاومت،‌ در هر لحظه برابر RI² است. مسئله زیر نیز مثال مناسبی جهت یادگیری مفهوم انرژی در القاگر است.

مثال ۶

مطابق با شکل زیر سیمی به طول بینهایت را در نظر بگیرید که حامل جریان I بوده و در سمت چپ حلقه‌ای مستطیلی به طول L و عرض w قرار گرفته است. ضریب القایی متقابل را برای این سیستم بیابید.

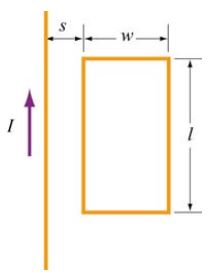
جهت محاسبه ضریب القایی دو طرفه (M)، در ابتدا بایستی شار مغناطیسی عبور کرده از حلقه‌ مستطیلی را محاسبه کرد. همان‌گونه که در مطلب مقدمه میدان مغناطیسی نیز عنوان شد، میدان مغناطیسی ناشی از سیم حامل جریان در فاصله r از آن برابر با $$B \enspace =\enspace \mu_0I/2 \pi r $$ است که با استفاده از قانون آمپر بدست آمده. نهایتا کل شار عبوری از سطح مستطیلی شکل را می‌توان با استفاده از انتگرال‌گیری روی دیفرانسیل dA=ldr،‌ به شکل زیر بدست آورد.

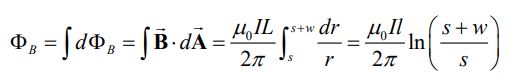
در نتیجه ضریب القایی متقابل برابر است با:

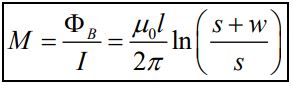
در مطالب آینده در مورد کاربرد مفهوم ارائه شده در مدارات RC ،RL و RLC صحبت خواهیم کرد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی برق و فیزیک آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی برق
• مجموعه آموزش‌های مهندسی برق
• میدان مغناطیسی ناشی از سیم حامل جریان -- از صفر تا صد
• فیزیک الکتریسیته را به سادگی و با مجموعه مقالات وبلاگ فرادرس یاد بگیرید
• مجموعه آموزش‌های نرم‌افزار‌های مهندسی برق و الکترونیک
• مجموعه آموزش‌های فیزیک