برنامه تشخیص وجود دور در گراف جهت دار – راهنمای کاربردی

در این مطلب، برنامه تشخیص وجود دور در گراف جهت دار در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java) و «پایتون» (Python) ارائه شده است. همچنین، در مطلب «برنامه بررسی وجود دور در گراف بدون جهت -- راهنمای کاربردی» نیز به روش تشخیص دور در گراف‌های بدون جهت پرداخته شده است. در ادامه، مساله تشخیص دور در گراف جهت‌دار، همراه با مثالی تشریح می‌شود. یک گراف جهت‌دار (Directed Graph) داده شده است و هدف بررسی این است که آیا گراف دارای دور است یا خیر. تابع باید در صورتی که گراف داده شده حاوی دستکم یک دور باشد مقدار True و در غیر این صورت مقدار False را بازگرداند. برای مثال، گراف زیر دارای سه دور از 0->2->0، 0->1->2->0 و 3->3 است. بنابراین تابع باید مقدار true را باز گرداند. می‌توان از «پیمایش اول عمق» (Depth First Traversal | DFS) برای شناسایی دور در گراف استفاده کرد. DFS برای گراف هم‌بند یک درخت تولید می‌کند. در گراف در صورتی که یال پشتی وجود داشته باشد، دور ایجاد می‌شود. یال پشتی، یالی است که از یک گره به خودش (خود-حلقه‌ای) و یا به والدین خود در درخت تولید شده توسط DFS متصل است. در گرافی که در ادامه می‌آید، سه یال پشتی وجود دارد که با ضرب‌در علامت گذاری شده‌اند. می‌توان مشاهده کرد که ۳ یال پشتی نشانگر ۳ دور نمایش داده شده در گراف هستند.

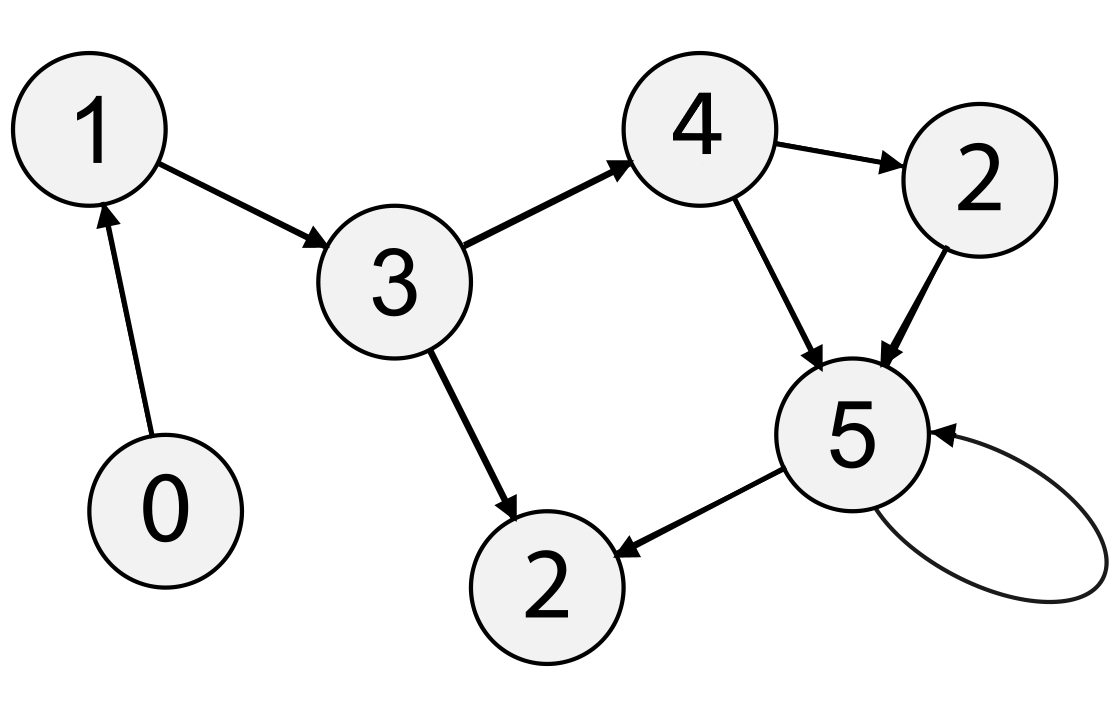
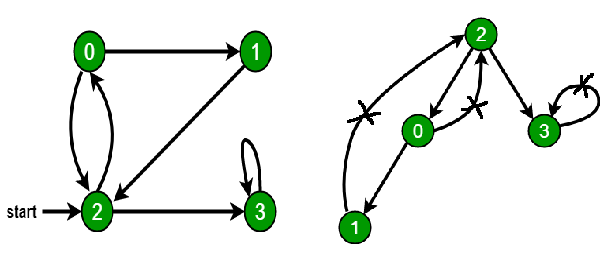
برای یک گراف غیر هم‌بند، جنگل DFS به عنوان خروجی گرفته می‌شود. برای شناسایی دور، می‌توان وجود یک چرخه در درخت‌های مجزا را با بررسی یال پشتی بررسی کرد. برای شناسایی یال پشتی، می‌توان راس‌های موجود در پشته بازگشتی تابع برای پیمایش DFS را دنبال کرد. اگر به راسی رسید که در حال حاضر در پشته بازگشتی قرار دارد، دور در درخت وجود دارد. یالی که راس کنونی را به راس موجود در پشته بازگشتی متصل می‌کند، یال پشتی است. در اینجا، از آرایه []recStack برای پیگیری راس‌ها در پشته بازگشتی استفاده می‌شود.

برنامه تشخیص وجود دور در گراف جهت دار در ++C

برنامه تشخیص وجود دور در گراف جهت دار در جاوا

برنامه تشخیص وجود دور در گراف جهت دار در پایتون

پیاده‌سازی و انجام عملیات مختلف مربوط به گراف در پایتون هم دارای اصول و قواعد یکسانی است. با این تفاوت که هر زبان سینتکس و قواعد گرامری مخصوص به خود را دارد. در زیر کدهای مربوط به برنامه تشخیص وجود دور در گراف جهت‌دار را در این زبان مشاهده می‌کنید.

خروجی

Graph contains cycle

پیچیدگی زمانی این روش، مشابه با پیچیدیگی زمانی پیمایش DFS و برابر با (O(V+E است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^