مختصات استوانه ای – به زبان ساده

همانطور که می‌دانید، شیوه نمایش مختصات سه بعدی در حالت استاندارد یعنی (x, y, z) را سیستم مختصات کارتزین می‌نامند. علاوه بر این مورد، شیوه‌های نمایش دیگری نیز برای نمایش مختصات سه بعدی وجود دارد که از جمله آن‌ها می‌توان به مختصات کروی و مختصات استوانه‌ای اشاره کرد.

این مطلب به صورت دقیق به بررسی مختصات استوانه‌ای می‌پردازد و روابط میان این دستگاه مختصات و دستگاه مختصات کارتزین را بیان می‌کند و در انتهای مطلب نیز با استفاده از چند مثال، شیوه نمایش صفحات مختلف در دستگاه مختصات استوانه‌ای را مورد بررسی قرار می‌دهد. البته در آینده انتگرال‌گیری در مختصات استوانه‌ای را نیز توضیح خواهیم داد.

مختصات استوانه‌ای

همانطور که اشاره شد، مختصات استوانه‌ای یکی از شیوه‌های نمایش یک نقطه در حالت سه بعدی است و برای نمایش آن، محورهای مختصات کارتزین را با استفاده از سه رابطه به رابطه‌ای جدید تبدیل می‌کنیم.

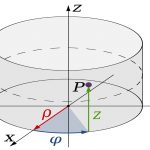
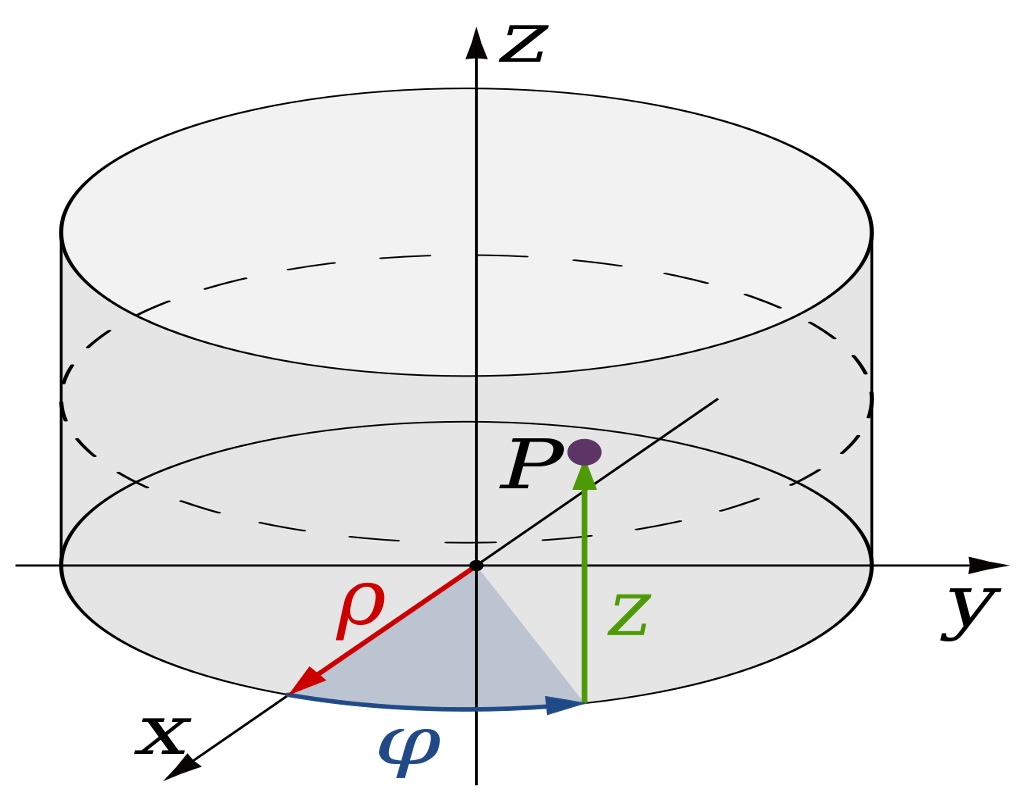
توجه کنید که از روابط بیان شده در مختصات قطبی برای بیان مختصات استوانه‌ای استفاده می‌شود و تنها مختصات z نیز به آن اضافه می‌گردد. شکل زیر نمایی از مختصات استوانه‌ای را در فضای سه بعدی به تصویر کشیده است.

بنابراین در صورتی که یک نقطه در مختصات استوانه‌ای موجود باشد، مختصات کارتزین را می‌توان با استفاده از روابط زیر مورد محاسبه قرار داد.

$${ \begin {align*} x & = { r } \cos \theta \\ { y } & = { r } \sin \theta \\ { z } & = { z } \end {align*} }$$

همانطور که مشاهده می‌شود، رابطه سوم بیان می‌کند که مختصات z در دستگاه مختصات کارتزین و استوانه‌ای یکسان است. به صورت مشابه می‌توان بیان کرد که اگر ما یک نقطه در دستگاه مختصات کارتزین داشته باشیم، مختصات استوانه‌ای را می‌توان با استفاده از روابط زیر مورد ارزیابی قرار داد.

$${ \begin {align*} r & = \sqrt { { x ^ 2 } + { y ^ 2 } } \end{align*} }$$

$${ \begin {align*} { r ^ 2 } = { x ^ 2 } + { y ^ 2 } \end{align*} }$$

$${ \begin {align*} \theta = { \tan ^ { - 1 } } \left ( { \frac { y } { x } } \right ) \end {align*} }$$

$${ \begin {align*} z = z \end{align*} }$$

در ادامه به کمک چند مثال، شیوه استفاده از دستگاه مختصات استوانه‌ای و همچنین بیان صفحات مختلف در این دستگاه مختصات مورد ارزیابی قرار می‌گیرد.

مثال 1

با استفاده از روابط ارائه شده برای مختصات استوانه‌ای، مشخص کنید که معادله زیر چه صفحه‌ای را نمایش می‌دهد.

$${ r = 5 }$$

در حالت دو بعدی رابطه $${ r = 5 }$$ نشان دهنده یک دایره به شعاع $${ 5 }$$ است. اما در اینجا ما در مختصات سه‌بعدی قرار داریم و معادله فوق نیز رابطه‌ای برای z بیان نکرده است. بنابراین می‌توان نتیجه گرفت که مقدار z به صورت آزاد، قابلیت تغییر دارد. بنابراین ما یک استوانه به شعاع $${ 5 }$$ داریم که محور آن روی محور z قرار گرفته است.

مثال 2

رابطه زیر را در نظر بگیرید.

$${ { r ^ 2 } + { z ^ 2 } = { 100 } }$$

این رابطه چه صفحه‌ای را مشخص می‌کند؟

فیلم آموزش ریاضی عمومی ۲ – جامع و کاربردی در فرادرس

کلیک کنید

برای تحلیل بهتر این رابطه، آن را به دستگاه مختصات کارتزین منتقل می‌کنیم. برای اینکار، از رابطه زیر برای تبدیل شعاع r به دستگاه مختصات کارتزین استفاده می‌شود.

$${ \begin {align*} { r ^ 2 } = { x ^ 2 } + { y ^ 2 } \end{align*} }$$

بنابراین رابطه صورت سوال را می‌توان به شکل زیر بازنویسی کرد.

$${ \begin {align*} { r ^ 2 } + { z ^ 2 } & = 100 \\ { x ^ 2 } + { y ^ 2 } + { z ^ 2 } & = 100 \end {align*} }$$

بنابراین این رابطه، نشان دهنده یک کره به شعاع $${ 10 }$$ است که مرکز آن در مرکز محور مختصات قرار دارد.

مثال 3

رابطه زیر چه صفحه‌ای را نمایش می‌دهد.

$${ z = r }$$

برای بیان این صفحه نیز باید فرم کارتزین و آشنای آن را بیابیم. بنابراین ابتدا طرفین رابطه فوق را به توان دو می‌رسانیم.

$${ \begin {align*} { z ^ 2 } = { r ^ 2 } \end {align*} }$$

همچنین با توجه به اینکه رابطه زیر در دستگاه مختصات استوانه‌ای برقرار است، رابطه فوق را می‌توانیم به فرم ساده‌تری بیان کنیم.

$${ \begin {align*} { r ^ 2 } = { x ^ 2 } + { y ^ 2 } \end{align*} }$$

$${ \begin {align*} { z ^ 2 } = { x ^ 2 } + { y ^ 2 } \end {align*} }$$

همانطور که از هندسه به یاد داریم، معادله نهایی فوق، یک مخروط را نشان می‌دهد. بنابراین با توجه به سه مثالی که در بالا بیان شد، برای تحلیل بهتر دستگاه مختصات استوانه‌ای، می‌توانیم به کمک روابط بیان شده، روابط مربوط به دستگاه مختصات استوانه‌ای و کارتزین را به یکدیگر تبدیل کنیم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• مجموعه آموزش‌های ریاضیات
• مختصات قطبی — از صفر تا صد
• انتگرال در مختصات استوانه‌ای -- از صفر تا صد
• مختصات کروی — به زبان ساده
• اتحاد و تجزیه در ریاضی — به زبان ساده

^^