جریان کوئت (Couette Flow) در مکانیک سیالات — از صفر تا صد

در مطالب قبلی وبلاگ فرادرس، معادلات ناویر-استوکس به صورت کامل مورد بررسی قرار گرفتند. همانطور که بیان شد، ویژگی‌های مختلف سیال به کمک معادلات ناویر-استوکس و معادله بقای جرم قابل محاسبه هستند. ولی از آنجایی که ترم‌های غیر خطی در معادلات ناویر-استوکس حضور دارند، عموماً برای حل آن‌ها از روش‌های عددی بهره گرفته می‌شود و تنها با استفاده از برخی ساده‌سازی‌ها، این معادلات دارای حل دقیق هستند. یکی از این ساده‌سازی‌ها در حالتی رخ می‌دهد که سیال، بین دو صفحه موازی، جریان دارد و یکی از این صفحات ساکن و صفحه دیگر با سرعت ثابت در حال حرکت است. به این نوع جریان، جریان کوئت گفته می‌شود. در این مطلب مفهوم جریان کوئت و روابط حاکم بر آن به صورت دقیق و به کمک یک مثال مورد بررسی قرار می‌گیرند.

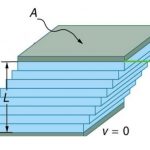
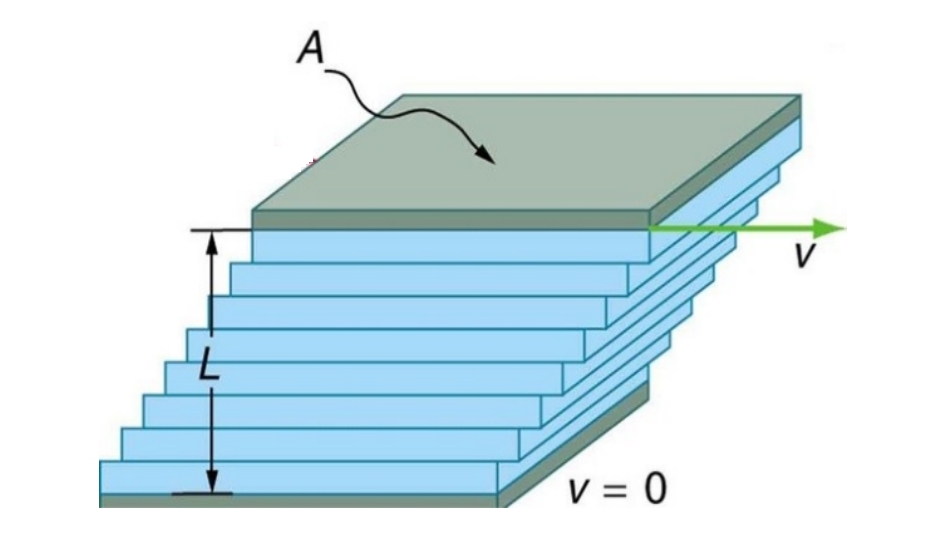
جریان کوئت

همانطور که اشاره شد، جریان کوئت به جریان سیال، بین دو صفحه موازی گفته می‌شود که در آن یکی از صفحات ساکن و صفحه دیگر با سرعت ثابت U در حال حرکت است. جزئیات این جریان را می‌توان به شکل زیر نمایش داد.

فیلم آموزش هیدرودینامیک – جامع و با حل مثال مختلف در فرادرس

کلیک کنید

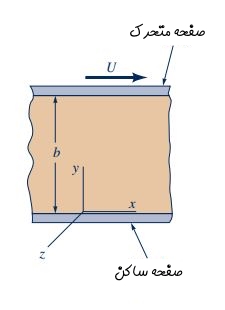
همانطور که در شکل بالا نشان داده شده، ذرات سیال در راستای x و موازی با دو صفحه بالا و پایین حرکت می‌کنند و این ذرات سرعتی در راستای y و z ندارند. بنابراین داریم:

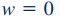
رابطه پیوستگی را که در مطالب قبلی وبلاگ فرادرس بیان کردیم در اینجا بازنویسی می‌کنیم:

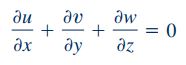
با جایگذاری روابط ۱ و ۲ در رابطه ۳، در نهایت عبارت زیر را برای جریان کوئت داریم:

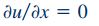
نکته دیگر در جریان بین دو صفحه موازی موسوم به جریان کوئت، این است که سرعت در راستای u) x)، هیچ تغییراتی در راستای z ندارد. همچنین در اینجا جریان به صورت پایا در نظر گرفته می‌شود. بنابراین با توجه به نکات ذکر شده و رابطه ۴، می‌توان نتیجه گرفت که سرعت در راستای x، تنها تابعی از متغیر y است و به شکل زیر نمایش داده می‌شود.

برای بازنویسی معادلات ناویر-استوکس علاوه بر روابطی که در قسمت قبل اشاره شد، باید ترم‌های شتاب را نیز مورد ارزیابی قرار دهیم. در جریان کوئت، تنها ترم شتاب، شتاب گرانش در راستای y است. بنابراین داریم:

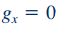
با جایگذاری روابط بالا در معادلات ناویر-استوکس در نهایت این معادلات به شکل زیر در می‌آیند.

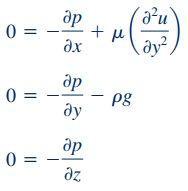
همانطور که مشاهده می‌شود، معادلات ناویر-استوکس در جریان کوئت بسیار ساده‌تر از شکل رایج این معادلات هستند. با انتگرال‌گیری از معادله ناویر-استوکس نشان داده شده در راستای y و z، رابطه زیر برای فشار به دست می‌آید:

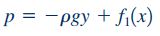
این رابطه نشان می‌دهد که در این جریان، فشار در راستای y به صورت هیدرواستاتیک تغییر می‌کند. برای ساده‌سازی معادلات حاکم بر جریان کوئت، معادله ناویر-استوکس در راستای x را به شکل زیر بازنویسی می‌کنیم.

در ادامه از طرفین این معادله، به شکل زیر انتگرال می‌گیریم:

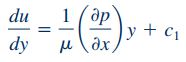
با انتگرال‌گیری دوباره از طرفین معادله بالا، رابطه زیر برای سرعت در راستای x، به دست می‌آید.

توجه کنید که در انتگرال‌گیری بالا، عبارت مشتق جزئی فشار در راستای x به عنوان یک ثابت در نظر گرفته شده و دلیل این امر این است که مطابق رابطه ۶، مشتق جزئی فشار در راستای x، تابعی از y نیست و می‌توان در انتگرال‌گیری فوق آن را ثابت فرض کرد.

نکته دیگر این است که در این رابطه دو ثابت $$C_{1}$$ و $$C_{2}$$ با استفاده از شرایط مرزی قابل محاسبه خواهند بود که در ادامه به بررسی آن‌ها می‌پردازیم.

برای محاسبه رابطه سرعت‌ سیال در جریان کوئت، مرکز محور مختصات را در صفحه‌ زیرین و فاصله بین دو صفحه را برابر با b فرض می‌کنیم. این مورد در شکل 1 نشان داده شده است.

دو شرط مرزی در جریان کوئت مطابق با روابط زیر، در نظر گرفته می‌شوند.

$$u=0\enspace \enspace \enspace@ \enspace y= 0$$

$$u=U\enspace \enspace \enspace@ \enspace y= b$$

این روابط نشان‌ دهنده شرط عدم لغزش است که مطابق این شرط، سیال در مجاورت یک صفحه با سرعتی برابر با سرعت همان صفحه حرکت می‌کند.

با اعمال شرایط مرزی بالا در رابطه ۸، می‌توان دو ثابت $$C_{1}$$ و $$C_{2}$$ را محاسبه کرد و در نهایت رابطه سرعت سیال در راستای x به شکل زیر در می‌آید.

این رابطه را به فرم بی‌بعد نیز می‌توان نوشت:

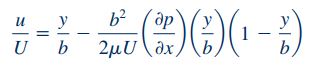
در رابطه بالا، سرعت u با استفاده از سرعت صفحه بالایی جریان کوئت و موقعیت y با استفاده از فاصله بین دو صفحه در جریان کوئت بی‌بعد شده‌اند. همچنین پارامتر بی‌بعد دیگری نیز به شکل زیر در این رابطه موجود است.

پروفیل‌های مختلفی برای سرعت سیال در جریان کوئت به شکل زیر قابل مشاهده هستند. شکل این پروفیل‌ها به متغیر بی‌بعد P در رابطه بالا بستگی دارد.

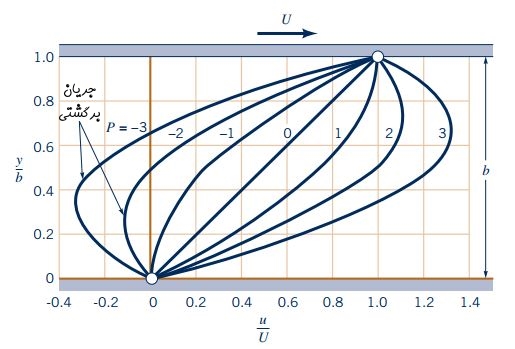
ساده‌ترین فرم جریان کوئت، حالتی است که گرادیان فشار صفر باشد. در این حالت، تنها حرکت صفحه بالایی، عامل حرکت سیال است. بنابراین رابطه ۹ برای سرعت سیال در جریان کوئت به شکل زیر بازنویسی می‌شود.

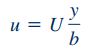
این رابطه نشان می‌دهد که سرعت سیال در حالتی که گرادیان فشار صفر است، به صورت خطی بین دو صفحه تغییر می‌کند. این مورد در شکل ۲ با $$P=0$$ به تصویر کشیده شده است.

جریان کوئت کاربرد بسیار زیادی در صنایع دارد. به عنوان مثال، شرایط توضیح داده شده در بالا را می‌توان در دو سیلندر هم‌مرکز مشاهده کرد که یکی از این سیلندرها ثابت و دیگری با سرعت دورانی ثابت $$\omega$$ می‌چرخد. این مورد در شکل زیر برای یک «یاتاقان استوانه‌ای» (Journal Bearing) نشان داده شده است.

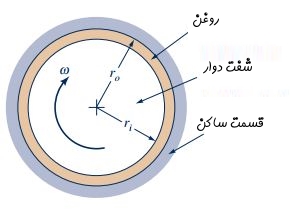
در صورتی که در یاتاقان استوانه‌ای فوق، فاصله‌ی بین دو محور بسیار کم باشد (رابطه 11) می‌توان از فرض جریان کوئت برای محاسبه خواص جریان در این یاتاقان استفاده کرد.

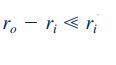
همانطور که اشاره شد، با استفاده از رابطه بالا می‌توان جریان سیال در یاتاقان استوانه‌ای را به صورت جریان کوئت در نظر گرفت. برای این مسئله سرعت، ضخامت و تنش برشی به شکل زیر در نظر گرفته می‌شوند.

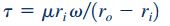
در ادامه با استفاده از یک مثال کاربرد روابط حاکم بر جریان کوئت در مسائل مکانیک سیالات مورد بررسی قرار داده می‌شود.

مثال

یک مخزن حاوی سیال ویسکوز را مطابق شکل زیر در نظر بگیرید. یک نواز نازک با سرعت $$V_{0}$$ به صورت عمودی از این مخزن عبور می‌کند. با توجه به حضور نیروهای لزج، بخشی از سیال با ضخامت h و در حضور نیروی گرانش توسط نواز نازک به سمت بالا حرکت می‌کند. در این حالت جریان به صورت لایه‌ای، پایا و کاملا توسعه یافته در نظر گرفته می‌شود. با استفاده از معادله ناویر-استوکس رابطه‌ای را برای سرعت میانگین لایه نازک سیالی بنویسید که مطابق شکل زیر توسط نوار نازک به سمت بالا حرکت می‌کند.

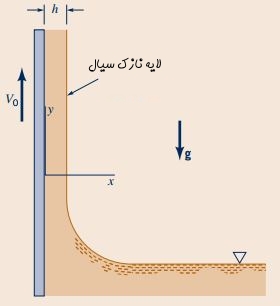
در این مثال، با توجه به آن‌که جریان به صورت کاملا توسعه یافته در نظر گرفته شده، تنها سرعت در راستای y موجود است که مقدار آن با v نشان داده می‌شود و می‌توان نتیجه گرفت u=v=0 است. در ادامه معادله پیوستگی را برای این مثال به شکل زیر بازنویسی می‌کنیم:

فیلم آموزش انتقال حرارت هدایتی CFD و کنترل انتقال حرارت به وسیله فین (رایگان) در فرادرس

کلیک کنید

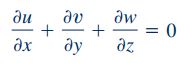
بنابراین با توجه به معادله پیوستگی، مشتق جزئی سرعت در راستای y، نسبت به y برابر با صفر می‌شود و از آنجایی که جریان به صورت پایا فرض شده، عبارت سرعت در راستای y، تنها تابعی از متغیر x خواهد بود. این روابط به شکل زیر قابل بیان هستند.

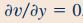
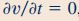
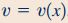
با استفاده از روابط بالا، معادله ناویر-استوکس در راستای x و z به شکل ساده‌ شده زیر بازنویسی می‌شوند.

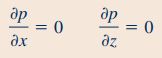
روابط بالا نشان می‌دهند که فشار در راستای افقی تغییر نمی‌کند. نکته دیگر این است که فشار در سطح لایه نازک سیال یعنی مکانی که x=h است، برابر با فشار اتمسفر در نظر گرفته می‌شود بنابراین فشار در تمام لایه نازک سیال برابر با فشار اتمسفر و در نتیجه فشار نسبی در این ناحیه صفر است.

با توجه به نکاتی که بیان شد، معادله ناویر-استوکس در راستای y را می‌توان به شکل زیر بازنویسی کرد.

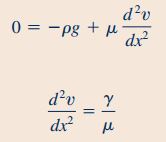
در ادامه از طرفین رابطه بالا یک بار انتگرال می‌گیریم.

در این مسئله فرض می‌شود که مقاومت هوا در سطح لایه نازک سیال یعنی x=h، برابر با صفر است. بنابراین تنش برشی در این نقطه را برابر با صفر در نظر می‌گیریم. برای این کار رابطه تنش برشی برای دو صفحه موازی را به شکل زیر می‌نویسیم.

در صورتی که مقدار تنش برشی در این رابطه را برابر با صفر قرار دهیم، ثابت موجود در معادله ناویر-استوکس در راستای y (رابطه 13) مطابق با رابطه زیر محاسبه می‌شود.

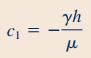
در ادامه از رابطه ۱۳ یک بار دیگر انتگرال می‌گیریم و در نهایت رابطه‌ای برای سرعت در راستای y به شکل زیر به دست می‌آید.

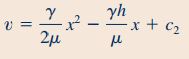
شرط مرزی دیگر این است که سیال در سطح نوار نازک (x=0) شرط عدم لغزش را ارضا می‌کند و سرعت آن برابر با سرعت نواز نازک ($$V_0$$) است. با جایگذاری این شرط مرزی در رابطه بالا ضریب $$c_2$$ به شکل زیر محاسبه می‌شود.

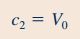
بنابراین فرم نهایی رابطه توزیع سرعت در سیالی که به وسیله نواز نازک بالا رفته است به شکل زیر در می‌آید.

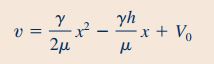
در ادامه به محاسبه سرعت میانگین سیال می‌پردازیم. در این قسمت با توجه به رابطه‌ای که که در مطلب پیوستگی و بقای جرم بیان شد، ابتدا باید نرخ جریان سیال بالارونده به وسیله نوار نازک را محاسبه کنیم. بنابراین به شکل زیر عمل می‌کنیم.

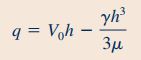
در ادامه با توجه به رابطه $$q=Vh$$، که در آن V سرعت میانگین سیال است، داریم:

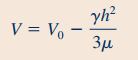
رابطه بالا سرعت میانگین سیالی را نشان می‌دهد که توسط نوار نازک به سمت بالا در حال حرکت است.

در این مطلب جریان کوئت مورد مطالعه قرار داده شد. این جریان کاربرد بسیار زیادی در مسائلی مانند یاتاقان‌ها دارد که در آن‌ها سیال، بین دو سطح موازی، جریان دارد که یکی از این سطوح ساکن و دیگری با سرعت ثابت در حال حرکت است. در انتهای این مطلب به کمک یک مثال کاربرد روابط حاکم بر جریان کوئت به صورت دقیق مورد بررسی قرار گرفت و نشان داده شد که معادلات ناویر-استوکس در این جریان، دارای جواب دقیق هستند.

در صورتی که به مطلب ارائه شده، علاقه‌مند هستید و قصد یادگیری بیشتر در زمینه مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• آموزش مکانیک سیالات
• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
• مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد
• سینماتیک سیالات — مقدمه‌ای بر مکانیک
• پیوستگی و بقای جرم در سیالات — از صفر تا صد

^^