معرفی اعداد شگفت انگیز یا اتومورفیک (Automorphic)
در ریاضیات به یک عدد زمانی عدد شگفت انگیز گفته میشود که n رقم آخر مربع عدد، برابر با خود عدد باشد. برای مثال 625 = 252 و 5776 = 762. این اعداد به نام اعداد اتومورفیک نیز نامیده میشوند.


اعداد اتومورفیک بزرگتری مانند 212890625 و 787109376 نیز وجود دارند:
2128906252 = 45322418212890625
و
7871093762 = 619541169787109376
همچنین باید بدانید که اگر n رقم آخر مربع عدد برابر با خود عدد باشد، این رابطه در مورد مکعب عدد و توانهای بالاتر نیز صدق میکند. مشخص شده است که برای هر n>1 دو عدد شگفت انگیز به طول n وجود دارد.
حتی یک فرمول نیز برای این دو عدد وجود دارد. فرمول نخست به صورت باقیمانده 5 به توان 2n تقسیم بر 10n است و دومی به صورت 10n + 1 منهای اولی است.
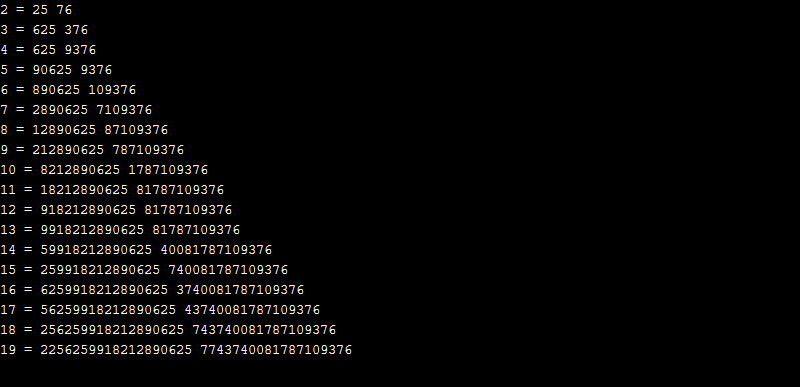
در کد پایتون زیر صحت این دو راهحل برای چند عدد نخست نشان داده شده است.
for i in range(2, 20):
a = (5**(2**i)) % (10**i)
b = 10**i - a + 1
print(i,"=" , a, b)
اعداد کروی
اعداد دایرهای یا کروی نیز نوع اندکی متفاوت از این اعداد هستند که توانهای آنها آخرین ارقام خود عدد هستند. تنها اعداد کروی 5، 6 و 10 هستند. توالی اعداد اتومورفیک به صورت 1، 5، 6، 235، 376، 625، 9376 و ... آغاز میشوند.
با توجه به عدد اتومورفیک k رقمی n که n>1 است، یک عدد اتومورفیک ’n با حداکثر 2k رقم با فرمول زیر قابل دسترسی است:
برای k های بالاتر از 1، حداکثر دو عدد اتومورفیک با k رقم وجود دارند که یکی با 5 و دیگری با 6 پایان مییابد. یکی از آنها به شکل زیر است:
مجموع دو عدد به صورت 10k + 1 است. عدد کوچکتر شاید کمتر از 10k − 1 باشد. برای نمونه برای k=4 آن دو عدد به صورت 9376 و 625 هستند. در این حالت تنها یک عدد اتومورفیک با k رقم است، عدد کوچکتر تنها در صورتی یک عدد اتومورفیک k رقمی تشکیل میدهد که 0 ابتدایی به ارقام آن اضافه شود.

توالی ارقام زیر میتوانند برای یافتن اعداد اتومورفیک k رقمی مورد استفاده قرار گیرند که k ≤ 1000 است.
12781 25400 13369 00860 34889 08436 40238 75765 93682 19796 26181 91783 35204 92704 19932 48752 37825 86714 82789 05344 89744 01426 12317 03569 95484 19499 44461 06081 46207 25403 65599 98271 58835 60350 49327 79554 07419 61849 28095 20937 53026 85239 09375 62839 14857 16123 67351 97060 92242 42398 77700 75749 55787 27155 97674 13458 99753 76955 15862 71888 79415 16307 56966 88163 52155 04889 82717 04378 50802 84340 84412 64412 68218 48514 15772 99160 34497 01789 23357 96684 99144 73895 66001 93254 58276 78000 61832 98544 26232 82725 75561 10733 16069 70158 64984 22229 12554 85729 87933 71478 66323 17240 55157 56102 35254 39949 99345 60808 38011 90741 53006 00560 55744 81870 96927 85099 77591 80500 75416 42852 77081 62011 35024 68060 58163 27617 16767 65260 93752 80568 44214 48619 39604 99834 47280 67219 06670 41724 00942 34466 19781 24266 90787 53594 46166 98508 06463 61371 66384 04902 92193 41881 90958 16595 24477 86184 61409 12878 29843 84317 03248 17342 88865 72737 66314 65191 04988 02944 79608 14673 76050 39571 96893 71467 18013 75619 05546 29968 14764 26390 39530 07319 10816 98029 38509 89006 21665 09580 86381 10005 57423 42323 08961 09004 10661 99773 92256 25991 82128 90625
با انتخاب k رقم از این توالی، یک عدد اتومورفیک به دست میآید؛ عدد دوم با کم کردن عدد از 10k + 1 به دست میآید.
عدد n-اتومورفیک
یک عدد n-اتومورفیک عددی مانند k است که ارقام آخر nk2 برابر با k باشد. برای مثال25392 = 3*922 و چون 25,392 با ارقام 92 خاتمه مییابد، از این رو 92 یک عدد 3-اتومورفیک است.
اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد میکنیم موارد زیر را نیز ملاحظه نمایید:
- عدد اویلر یا نپر – به زبان ساده
- اعداد مختلط – به زبان ساده
- آموزش های ریاضیات
- الگوها و دنباله های متداول عددی – به زبان ساده
- اعداد حقیقی — به زبان ساده
- آموزش های رایگان ریاضی و فیزیک
==













سلام ببخشید عدد شماره 5 و 6 اولی را چگونه پیدا میکنید
اون کد پایتون و همچنین فرمولی که گفتید درست نیست چون این جوابی که نمایش میدید رو نمیده
با سلام و احترام؛
صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم.
کد مربوطه در محیط Google Colab تست شد و خروجی آن دقیقاً مطابق با تصویری است که در این مطلب قرار داده شده است.
در صورتی که همچنان مشکلی وجود دارد، لطفاً دقیقتر اشکال را شرح بدهید تا امکان بررسی بیشتر وجود داشته باشد.
برای شما آرزوی سلامتی و موفقیت داریم.
سلام میشه همین کد پایتون رو که نوشتید طوری بنویسید که n رو بگیره و n امین عدد از اعداد اتومورفیک رو چاپ کنه ممنون
سلام مطلب خوبی بود فقط اولین قطعه کد خروجی نامناسب میدهد(تمامی خروجی ها به صورت 0 0 میباشد)
دوست عزیز کد منبع دارای اشکالی بود که اصلاح و تست شد. اینک میتوانید از فرمول تولید اعداد اتومورفیک استفاده نمایید.