منحنی یادگیری — کاربرد معادلات دیفرانسیل
همیشه کسب مهارت و تخصص در یک زمینه جدید مقداری زمان خواهد برد. منحنی یادگیری نموداری است که در آن، رابطه تعداد تلاشهای یک فرد برای یادگیری یک کار خاص را با سطح عملکرد او در انجام آن کار نشان میدهد. در این آموزش، مدل فرایند یادگیری را با استفاده از یک معادله دیفرانسیل به دست میآوریم.
ابتدا، تابع یادگیری قابل اندازهگیری $$ L ( t ) $$ را معرفی میکنیم. این تابع، برای مثال، ممکن است بهرهوری نیروی کار فعلی را توصیف کند. فرض کنید $$ {L_{\max }} $$ حداکثر مقدار قابل دسترس $$ L ( t) $$ باشد. در بسیاری از موارد، استفاده از یک قاعده سرانگشتی برای محاسبات کارساز خواهد بود: سرعت یادگیری متناسب با حجم موارد باقیمانده (یاد گرفته نشده) است.
از نظر ریاضی، این موضوع را میتوان به صورت زیر نشان داد:
$$ \large \frac { { d L } } { { d t } } = k \left ( { { L _ { \max } } – L } \right ) , $$
که در آن، $$k$$ ضریب تناسب است. معادله بالا، یک معادله دیفرانسیل جداشدنی است؛ بنابراین، میتوان آن را به سادگی در فرم عمومی حل کرد:
$$ \large \begin {align*} & \frac { { d L } } { { d t } } = k \left ( { { L _ { \max } } – L } \right ) , \; \; \Rightarrow { \frac { { d L } } { { { L _ { \max } } – L } } = k d t , \; \; } \Rightarrow { \int { \frac { { d L } } { { { L _ { \max } } – L } } } = \int { k d t } , \; \; } \\ & \Rightarrow { { - \int { \frac { { d \left ( { { L _ { \max } } – L } \right ) } } { { { L _ { \max } } – L } } } } = { \int { k d t } , \; \; } } \Rightarrow { { - \ln \left ( { { L _ { \max } } – L } \right ) } = { k t + \ln C , \; \; } } \\ & \Rightarrow { { \ln \left ( { { L _ { \max } } – L } \right ) } = { – k t + \ln C , \; \; } } \Rightarrow { { \ln \left ( { { L _ { \max } } – L } \right ) } = { \ln { e ^ { – k t } } } + { \ln C . } } \end {align*} $$
پس از حذف لگاریتمها، جواب عمومی به فرم زیر به دست میآید:
$$ \large { L _ { \max } } – L = C { e ^ { – k t } } . $$
ثابت $$ C$$ را میتوان از شرایط اولیه $$ L ( t = 0 ) = M $$ به دست آورد؛ یعنی $$C = {L_{\max }} – M $$. در نتیجه، منحنی یادگیری با فرمول زیر توصیف میشود:
$$ \large { L \left ( t \right ) = { L _ { \max } } } - { \left ( { { L _ { \max } } – M } \right ) { e ^ { – k t } } . } $$
پارامتر $$M$$ در عبارت بالا، سطح اولیه دانش یا مهارت را نشان میدهد. در سادهترین حالت، میتوان فرض کرد $$ M = 0 $$. پارامتر دیگر $$k$$ سرعت بالا رفتن نمودار است. منحنیهای یادگیری به ازای مقادیر مختلف $$M$$ و $$k$$، به ترتیب، در شکلهای ۱ و ۲ نشان داده شدهاند.
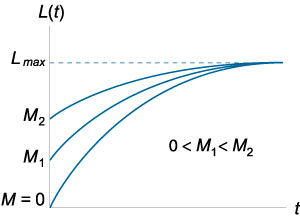
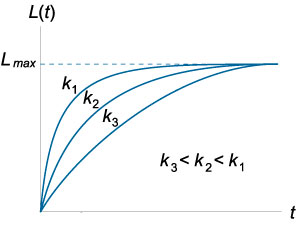
همانطور که میبینیم، سطح یادگیری $$L$$ در همه موارد در ابتدای فرایند افزایش مییابد، و پس از آن نرخ یادگیری با رسیدن سطح یادگیری $$L$$ به حداکثر مقدار $${L_{\max }} $$ کاهش مییابد.
مثالهای منحنی یادگیری
در این بخش دو مثال را از منحنی یادگیری بیان میکنیم.
مثال ۱
به طور معمول، یک نسخهخوان در داروخانه باید ۱۰۰۰ نسخه را در روز بررسی کند. فرض کنید یک نسخهخوان جدید در داروخانهای استخدام شده و در هفته اول قادر است ۱۰۰ نسخه را در روز بررسی کند. تعداد نسخههایی را به دست آورید که او میتواند در هفته دوم بررسی کند.
حل: با قرار دادن سطح مهارت اولیه برابر با صفر ($$ M = 0 $$)، میتوانیم فرایند یادگیری را به صورت زیر توصیف کنیم:
$$ \large L \left ( t \right ) = { L _ { \max } } \left ( { 1 – { e ^ { – k t } } } \right ) . $$
پارامتر $$k$$ را با دانستن تعداد نسخههای هفته اول، به صورت زیر تعیین میکنیم:
$$ \large \begin {align*}
& 1 0 0 = 1 0 0 0 \left ( { 1 – { e ^ { – k t } } } \right ) , \; \; \Rightarrow { 1 – { e ^ { – k t } } = 0 . 1 , \; \; } \\ & \Rightarrow { { e ^ { – k t } } = 0 . 9 , \; \; } \Rightarrow { - k t = \ln 0 . 9 , \; \; } \Rightarrow { k = – \frac { { \ln 0 . 9 } } { t } . }
\end {align*} $$
با جایگذاری $$ t = 1 $$ هفته، خواهیم داشت:
$$ \large k = – \frac { { \ln 0 . 9 } } { 1 } \approx – 0 . 1 0 5 $$
اکنون میتوانیم بهرهوری نسخهخوان را برای هفته دوم محاسبه کنیم:
$$ \large \begin {align*}
L \left ( { t = 2 } \right ) & = { 1000 \left ( { 1 – { e ^ { – 0 . 1 0 5 \cdot 2 } } } \right ) } = { 1 0 0 0 \left ( { 1 – { e ^ { – 0 . 2 1 } } } \right ) } \\ & \approx { 1 0 0 0 \left ( { 1 – 0 . 8 1 1 } \right ) } = { 1 8 9 \left [ { \frac { \text{receipts} } { \text {day} } } \right ] . }
\end {align*} $$
مثال ۲
فرض کنید یک خبر از یک رسانه جمعی بر اساس منحنی یادگیری پخش میشود. درصد اولیه جمعیتی که باید از این اخبار مطلع شوند باید چقدر باشد تا این خبر در هفته اول به ۵۰ درصد جمعیت و در هفته دوم به ۹۰ درصد آنها برسد؟
حل: اخبار با قانون زیر پخش میشود:
$$ \large L \left ( t \right ) = { L _ { \max } } – M { e ^ { – k t } } . $$
دو نقطه از این منحنی معلوم هستند: در هفته $$ t = 1 $$ و در هفته $$ t = 4 $$. بنابراین، میتوانیم دو معادله زیر را بنویسیم:
$$ \large { \left \{ \begin {array} {l}
L \left ( { t = 1 } \right ) = { L _ { \max } } – r { L _ { \max } }{ e ^ { – k \cdot 1 } } \\
L \left ( { t = 4 } \right ) = { L _ { \max } } – r { L _ { \max } } { e ^ { – k \cdot 4 } }
\end {array} \right . , \; \; } \Rightarrow
{ \left\{ \begin {array} {l}
0 . 5 { L _ { \max } } = { L _ { \max } } – r { L _ {\max }}{ e ^ { – k \cdot 1 } } \\
0 . 9 { L _ { \max } } = { L _ { \max } } – r { L _ { \max } }{ e ^ { – k \cdot 4 } }
\end {array} \right . } $$
در اینجا، $$M$$ به صورت $$r{L_{\max }} $$ نشان داده شده است، که در آن، $$r$$ در بازه $$0 \le r \le 1 $$ قرار دارد و زمان $$t$$ بر حسب هفته است.
با تقسیم روابط بر $$ {L_{\max }} $$، یک دستگاه معادلات برای متغیرهای مجهول $$r$$ و $$ k $$ خواهیم داشت:
$$ \large { \left \{ \begin {array} {l}
0 . 5 = 1 – r { e ^ { – k } } \\
0 . 9 = 1 – r { e ^ { – 4 k } }
\end {array} \right . , \; \; } \Rightarrow { \left \{ \begin {array} {l}
r { e ^ { – k } } = 0 . 5 \\
r { e ^ { – 4 k } } = 0 . 1
\end {array} \right . . } $$
با لگاریتم گرفتن از معادلات، داریم:
$$ \large \left \{ \begin {array} {l}
\ln r – k = \ln 0 . 5 \\
\ln r – 4 k = \ln 0 . 1
\end {array} \right . . $$
اکنون، با ضرب $$-4$$ در معادله اول، و پس از آن، جمع دو معادله، پارامتر $$k$$ را از معادلات حذف میکنیم:
$$ \large \begin {align*} { \left . { \left \{ \begin {array} {l}
– 4 \ln r + 4 k = – 4 \ln 0 . 5 \\
\ln r – 4 k = \ln 0 . 1
\end {array} \right . } \right | + , \; \; } & \Rightarrow
{ – 3 \ln r = \ln 0 . 1 – 4 \ln 0 . 5 , \; \; } \\ & \Rightarrow
{ \ln r = \frac { 1 } { 3 } \left ( { 4 \ln 0 . 5 – \ln 0 . 1 } \right ) . } \end {align*} $$
با انجام محاسبات ساده، جواب زیر به دست میآید:
$$ \large \begin {align*} \ln r & = \frac { 1 } { 3 } \left ( { 4 \ln 0 . 5 – \ln 0 . 1 } \right )
\approx { \frac { 1 } { 3 } \left [ { 4 \cdot \left ( { – 0 . 6 9 3 } \right ) – \left ( { – 2 . 3 0 2 } \right ) } \right ] }
\\ &= { \frac { 1 } { 3 } \left ( { – 0 . 4 6 9 } \right ) }
= { – 0 . 1 5 6 } \end {align*} $$
بنابراین، پارامتر $$r$$ برابر است با:
$$ \large r = { e ^ { – 0 . 1 56 } } \approx 0 . 8 5 5 $$
بنابراین، در این حالت، سطح اولیه نفوذ اخبار باید به صورت زیر باشد:
$$ \large \begin {align*}
L \left ( { t = 0 } \right ) & = { L _ { \max } } – r { L _ { \max } }
= { { L _ { \max } } – 0 . 8 5 5 { L _ { \max } } } \\ &
= { 0 . 1 4 5 { L _ { \max } } }
\approx { 1 5 \% { L _ { \max } } . }
\end {align*}$$










