ممان اینرسی چیست؟ + روش محاسبه و فرمول به زبان ساده
ممان اینرسی یا لختی دورانی، مقاومتی است که اجسام در هنگام شروع به حرکت دایرهای یا توقف از حرکت دایرهای از خود به نمایش میگذارند. اجسام، همواره تمایل دارند وضعیت فعلی خود را حفظ کنند و هنگام تغییر وضعیت (از حالت سکون به حرکت یا حرکت به سکون)، مقاومت مشخصی را از خود به نمایش میگذارند. این مقاومت که به جرم جسم بستگی دارد، با عنوان اینرسی شناخته میشود. اگر تغییر وضعیت، در حرکت دورانی و شتاب زاویهای مد نظر باشد، به مقاومت مذکور، ممان اینرسی/لختی دورانی میگویند. ممان اینرسی، از مباحث مهم در علوم مهندسی به شمار میرود. در این مقاله، به معرفی تعاریف و فرمول ممان اینرسی به همراه حل چند مثال میپردازیم. علاوه بر این، فرمول ممان اینرسی اشکال معروف هندسی را نیز معرفی میکنیم.
- تعریف ممان اینرسی و ارتباط آن با حرکت دورانی را یاد میگیرید.
- میآموزید گشتاور و انواع آن را چگونه تشخیص داده و محاسبه کنید.
- نحوه استفاده از فرمولهای ممان اینرسی برای اشکال رایج را خواهید آموخت.
- یاد خواهید گرفت گشتاور دوم سطح با ممان اینرسی چه تفاوتی دارد.
- خواهید آموخت چگونه از جدولها و ابزارهای آنلاین برای محاسبه لختی دورانی بهره بگیرید.
- تمرین میکنید چگونه ممان اینرسی را در مسائل مهندسی محاسبه کنید.


گشتاور چیست ؟
گشتاور، لنگر یا اصطلاحا «ممان» (Moment)، یک کمیت فیزیکی است که تاثیر نیروی اعمال شده بر یک نقطه از جسم را بر روی پیچش دیگر نقاط آن نمایش میدهد. از اینرو، این کمیت، با عنوان «گشتاور پیچشی» (Torque) نیز شناخته میشود. برای درک بهتر مفهوم گشتاور، تصویر زیر را در نظر بگیرید.
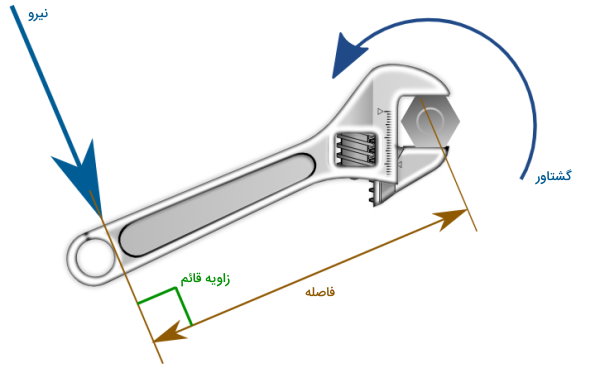
در تصویر بالا، یک پیچ توسط آچار در حال بسته شدن است. شخصی که آچار را در دست دارد، به دسته آن نیرو وارد میکند. این نیرو، در انتهای آچار به صورت گشتاور به پیچ اعمال میشود و آن را در جهت باز یا بسته شدن میچرخاند. گشتاور، برابر با حاصلضرب نیرو در فاصله است. فرمول گشتاور معمولا به صورت زیر نوشته میشود:
- M: گشتاور
- F: نیروی اعمال شده
- d: فاصله از محل اعمال نیرو
- α: زاویه بین راستای اعمال نیرو با d (در صورت راست بودن زاویه، عبارت سینوسی برابر با ۱ و از رابطه حذف میشود.)
مثال ۱: محاسبه گشتاور وارد به پیچ
شخصی در هنگام باز کردن یک پیچ، نیرویی معادل ۱۲۰ نیوتون را به دسته آچار وارد میکند. اگر فاصله بین دست تا پیچ برابر با ۰/۳ متر و زاویه بین دست با راستای این فاصله، برابر با ۱۱۵ درجه باشد، گشتاور وارد بر پیچ چقدر خواهد بود؟
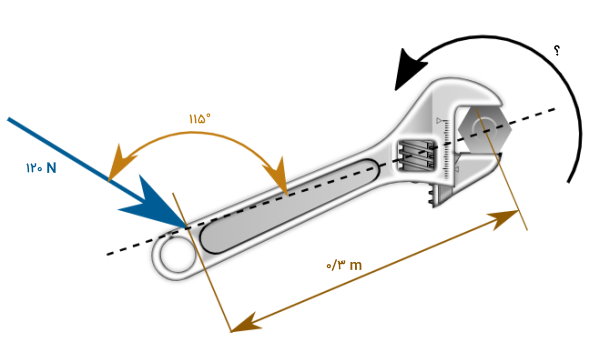
تصویر بالا، پارامترهای معلوم و مجهول در صورت سوال را نمایش میدهد. بر اساس فرمول گشتاور، داریم:
- M: گشتاور وارد بر پیچ
- F: نیروی اعمال شده بر آچار برابر با ۱۲۰ نیوتن
- d: فاصله از محل اعمال نیرو برابر با ۰/۳ متر
- α: زاویه بین راستای اعمال نیرو با d برابر با ۱۱۵ درجه
مقادیر معلوم را درون فرمول قرار میدهیم:
در نتیجه، گشتاور وارد بر پیچ، برابر با ۳۲/۶۳ نیوتن متر است.
انواع گشتاور کدام هستند ؟
در حالت کلی، گشتاور، به صورت حاصلضرب نیرو در فاصله تعریف میشود. این کمیت، انواع مختلفی دارد. از انواع پرکاربرد گشتاور میتوان به موارد زیر اشاره کرد:
- گشتاور اول سطح
- گشتاور اول جرم
- گشتاور دوم سطح
- گشتاور دوم جرم
«گشتاور اول سطح» (First Moment of Area)، از ضرب اندازه سطح (مساحت) در فاصله تا مرکز جرم سطح به دست میآید. این فاصله میتواند نسبت به محور X یا محور Y باشد. گشتاور اول سطح، معمولا به منظور تعیین موقعیت مرکز جرم مورد استفاده قرار میگیرد. این کمیت، با حرف Q نمایش داده میشود. تعریف گشتاور اول جرم نیز به همین شکل است؛ با این تفاوت که این گشتاور از ضرب اندازه جرم در فاصله تا مرکز جرم به دست میآید. در مجموع، مرکز جرم، پارامتر بسیار مهمی در محاسبه گشتاور اول است.
گشتاور دوم سطح چیست ؟
«گشتاور دوم سطح» (Second Moment of Area)، یکی از مشخصات هندسی جسم است که نحوه توزیع سطوح آن نسبت به یک محور دلخواه را نمایش میدهد. این مشخصه معمولا با حرف I یا J نمایش داده میشود. گشتاور دوم سطح، از رابطه انتگرالی زیر به دست میآید:
مفهوم گشتاور دوم سطح، چندین شباهت و تفاوت با مفهوم گشتاور دوم جرم دارد. در بخشهای بعدی، به معرفی این شباهتها و تفاوتها خواهیم پرداخت. پیش از این، باید مفهوم اینرسی را تعریف کنیم.
اینرسی چیست ؟
لختی یا «اینرسی» (Inertia)، کمیتی برای نمایش توانایی جسم برای مقابله در برابر تغییر وضعیت سکون یا حرکت است. اینرسی، از جرم مواد نشات میگیرد. هرچه جرم یک جسم بیشتر باشد، اینرسی آن بیشتر خواهد بود. به عبارت دیگر، به حرکت درآوردن آن از حالت سکون یا متوقف کردن آن در حین حرکت سختتر میشود.

به عنوان مثال، یک سنگ کوچک و یک سنگ بزرگ را در نظر بگیرید. پرتاب سنگ کوچک، سادهتر از پرتاب سنگ بزرگ است. در واقع، سنگ کوچک، مقاومت کمتر در برابر تغییر وضعیت از خود نشان میدهد. این تفاوت، به دلیل تفاوت در جرم سنگها و اینرسی آنها است. سنگهای کوچک، به دلیل وزن کمترشان، اینرسی کمتری دارند. به همین دلیل، راحتتر میتوان آنها را پرتاب کرد (از حالت سکون به حالت حرکت درآورد).
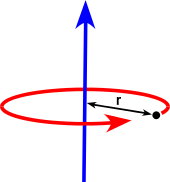
لختی دورانی یا ممان اینرسی چیست ؟
در بخشهای قبلی، با مفهوم ممان یا گشتاور و انواع آن آشنا شدیم و فهمیدیم که اینرسی، اساسا همان جرم اجسام است. با این پیشزمینه، به سراغ تعریف ممان اینرسی میرویم. در حرکت دورانی یا حرکت دایرهای، جسم حول یک محور ثابت میچرخد. به این ترتیب، تمام ذرات جسم، بر روی یک مسیر دایرهای شکل و با سرعت ثابت، دوران میکنند. در این شرایط، حرکت ذرات، با یک شتاب زاویهای همراه است.
لختی دورانی یا «ممان اینرسی» (Moment of Inertia)، توانایی جسم برای مقاومت در برابر شتاب زاویهای است. این کمیت، از جمع حاصلضربهای جرم هر ذره در مربع فاصله آن ذره تا محور دوران به دست میآید. ممان اینرسی، با عنوان گشتاور دوم جرم نیز شناخته میشود.
فرمول ممان اینرسی چیست ؟
ممان اینرسی، با حرف I نمایش داده میشود. فرمول این کمیت عبارت است از:
- I: ممان اینرسی
- mi: جرم ذره i ام
- ri: فاصله ذره i ام از محور دوران
فرم انتگرالی فرمول ممان اینرسی به صورت زیر نوشته میشود:
اهمیت و کاربرد ممان اینرسی چیست ؟
ممان اینرسی، از مشخصات جرمی اشیا است که پایداری و نیروی مورد نیاز برای به حرکت درآوردن آنها را توصیف میکند. به همین دلیل، این مشخصه به عنوان یکی از پارامترهای بسیار مهم در طراحی قطعات و سازههای مهندسی مورد استفاده قرار میگیرد. مهندسی مکانیک، هوافضا، عمران و خودروسازی، از حوزههای شناخته شده در زمینه کاربرد لختی دورانی هستند.
ممان اینرسی، به ما نشان میدهد که برای رسیدن به یک شتاب زاویهای مشخص، به چه مقدار گشتاور یا نیروی دورانی نیاز داریم. با ضرب این کمیت در شتاب زاویهای، گشتاور یا نیروی مورد نیاز به دست میآید. هر چه ممان اینرسی بیشتر باشد، گشتاور مورد نیاز نیز بیشتر خواهد بود. طراحان با محاسبه دقیق این پارامتر میتوانند بین ابعاد، وزن و کارایی سازه، تعادل خوبی را برقرار کنند.
مثال ۲: محاسبه ممان اینرسی
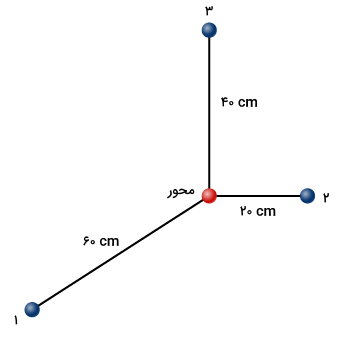
تصویر زیر، سیستمی متشکل از چندین ذره نقطهای را نمایش میدهد. هر ذره، ۰/۳ کیلوگرم جرم داشته و تمام ذرات بر روی یک صفحه مشترک قرار دارند. با توجه به موقعیت قرارگیری محور دوران، ممان اینرسی سیستم را به دست بیاورید.
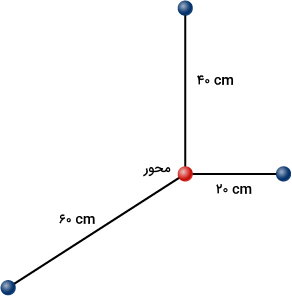
برای به دست آوردن ممان اینرسی یا لختی دورانی سیستم بالا، ابتدا هر یک از نقاط ذرهای را شمارهگذاری میکنیم.
فرمول لختی دورانی برای این سیستم، به صورت زیر نوشته میشود:
- I: ممان اینرسی
- mi: جرم ذره i ام
- ri: فاصله ذره i ام از محور دوران
به دلیل وجود سه نقطه در سیستم، فرمول بالا را به فرم زیر بازنویسی میکنیم:
از آنجایی که جرم تمام ذرات برابر است، نیازی به نوشتن آنها با اندیس جداگانه نیست:
از جرم m فاکتور میگیریم:
پارامترهای رابطه بالا عبارت هستند از:
- I: ممان اینرسی سیستم
- m: جرم ذرات برابر با ۰/۳ کیلوگرم
- r۱: فاصله ذره اول تا محور برابر با ۶۰ سانتیمتر
- r۲: فاصله ذره اول تا محور برابر با ۲۰ سانتیمتر
- r۳: فاصله ذره اول تا محور برابر با ۴۰ سانتیمتر
در صورت سوال، فاصلهها بر حسب سانتیمتر داده شدهاند. برای حل مسئله، باید واحد آنها را به متر تبدیل کنیم. بنابراین داریم:
- I: ممان اینرسی سیستم
- m: جرم ذرات برابر با ۰/۳ کیلوگرم
- r۱: فاصله ذره اول تا محور برابر با ۰/۶ متر
- r۲: فاصله ذره اول تا محور برابر با ۰/۲ متر
- r۳: فاصله ذره اول تا محور برابر با ۰/۴ متر
اکنون، مقادیر بالا را در رابطه ممان اینرسی قرار میدهیم:
در نتیجه، ممان اینرسی سیستم مورد سوال برابر با ۰/۱۶۸ کیلوگرم در متر مربع است.
قضیه محورهای موازی در محاسبه ممان اینرسی
برای اغلب اجسام، ممان اینرسی، حول محور گذرنده از مرکز جرم محاسبه میشود. «قضیه محورهای موازی» (Parallel Axis Theorem)، به منظور محاسبه این کمیت، حول محورهای دیگر مورد استفاده قرار میگیرد. بر اساس این قضیه، ممان اینرسی یک جسم، حول محوری موازی با محور گذرنده از مرکز جرم آن، از جمع ممان اینرسی جسم حول محور گذرنده از مرکز جرم با حاصلضرب جرم جسم در مربع فاصله دو محور به دست میآید. 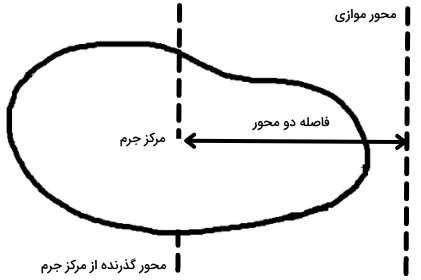
برای درک بهتر این قضیه، تصویر بالا را در نظر بگیرید. ممان اینرسی جسم، حول محور موازی برابر است با:
- I: ممان اینرسی جسم حول محور موازی
- Ic: ممان اینرسی جسم حول محور گذرنده از مرکز جرم
- M: جرم جسم
- h: فاصله بین محور گذرنده از مرکز جرم و محور موازی با آن
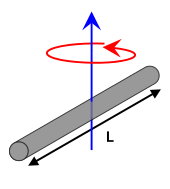
مثال ۳: تعیین فرمول ممان اینرسی میله استوانه ای
یک میله استوانهای به طول L و جرم M را در نظر بگیرید. لختی دورانی این میله را حول محور مرکزی به دست بیاورید. با استفاده از قضیه محورهای موازی، لختی دورانی حول محور موازی با محور مرکزی و گذرنده از انتهای میله را تعیین کنید.
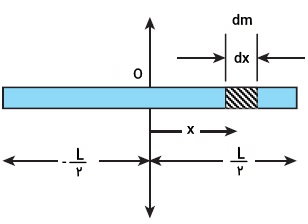
تصویر بالا، محور گذرنده از مرکز جرم میله استوانهای (O) و دیگر اندازههای مورد نیاز برای محاسبه گشتاور دوم جرم را نمایش میدهد. بر خلاف مثال ۲ (سیستم نقاط ذرهای)، اجزای یک میله، پیوسته هستند. به همین دلیل، برای به دست آوردن ممان اینرسی، باید فرم انتگرالی استفاده کنیم:
به دلیل توزیع یکنواخت جرم در میله، جرم بر واحد طول (λ) برابر است با:
اگر جرم جزئی میله (dm) را در نظر بگیریم، خواهیم داشت:
جرم بر واحد طول را در رابطه بالا قرار میدهیم:
dx، از تا تغییر میکند. با در نظر داشتن این موضوع و رابطه بالا، فرمول انتگرالی ممان اینرسی را بازنویسی میکنیم:
، معلوم است. بنابراین، این کسر از انتگرال خارج و به پشت آن منتقل میشود:
انتگرال x۲ برابر است با:
جواب این انتگرال را در بازه تا در رابطه I قرار میدهیم:
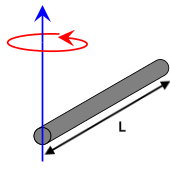
رابطه بالا، فرمول ممان اینرسی میله استوانهای شکل، حول محور گذرنده از مرکز جرم آن است. برای به دست آوردن ممان اینرسی، حول محور موازی و گذرنده از انتهای میله، دو راه حل داریم.
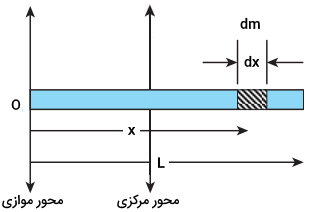
راه حل اول، استفاده از رابطه انتگرال (بخش اول مثال) است. راه حل دوم، استفاده از قضیه محورهای موازی است. بر اساس این قضیه، داریم:
- I: ممان اینرسی جسم حول محور موازی
- Ic: ممان اینرسی جسم حول محور گذرنده از مرکز جرم
- M: جرم جسم
- h: فاصله بین محور گذرنده از مرکز جرم و محور موازی با آن
با توجه به نتایج بخش اول سوال، ممان اینرسی جسم حول محور گذرنده از مرکز جرم برابر است با:
فاصله بین محور گذرنده از مرکز جرم و محور موازی با آن، برابر است با:
این روابط را درون قضیه محورهای موازی قرار میدهیم:
به این ترتیب، فرمول ممان اینرسی میله استوانهای به طول L و جرم M برای محورهای موازی به دست آمد. برای اطمینان از صحت این فرمول، میتوان بار دیگر از روش انتگرالی نیز به آن رسید.
ممان اینرسی اجسام و اشکال مختلف
در این بخش، به معرفی فرمول ممان اینرسی برخی از اجسام و اشکال معروف و پرکاربرد میپردازیم.
فرمول ممان اینرسی نقطه چیست ؟
برای جرمهای نقطهای، هیچ ممان اینرسی حول محور گذرنده از مرکز جرم تعریف نمیشود. از اینرو، لختی دورانی آنها با استفاده از قضیه محورهای موازی به دست میآید. تصویر زیر را در نظر بگیرید. این تصویر، جرم نقطهای M در فاصله r از یک محور موازی را نمایش میدهد.
با توجه به قضیه محورهای موازی، لختی دورانی نقطه برابر است با:
فرمول ممان اینرسی دو نقطه چیست ؟
سیستمی با دو جرم نقطهای m۱ و m۲ با جرم کاهشیافته μ را در نظر بگیرید.
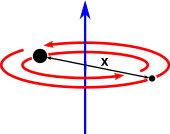
ممان اینرسی این سیستم حول محور گذرنده از مرکز جرم آن (مرکز جرم کل سیستم)، از رابطه زیر به دست میآید:
x، فاصله عمودی بین دو نقطه است.
ممان اینرسی میله چیست ؟
در مثال ۳، فرمول ممان اینرسی میله را تعیین کردیم. برای میلهای به طول L، جرم m و محور گذرا از مرکز جرم، این فرمول به صورت زیر نوشته میشود:
فرمول ممان اینرسی میله حول محورهای موازی انتهایی نیز عبارت است از:
در فرمولهای ارائه شده، فرض میشود که میله، طول بینهایت نازک اما ساختاری صلب دارد.
ممان اینرسی حلقه دایره ای چیست ؟
تصویر زیر، یک حلقه دایرهای به شعاع r و جرم m را نمایش میدهد.
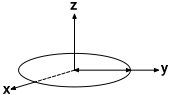
ممان اینرسی حلقه، حول محورهای افقی x و y و محور عمودی z برابر است با:
ممان اینرسی حلقه دارای ضخامت چیست ؟
اگر حلقه، دارای ضخامت (شعاع داخلی r۱ و شعاع خارجی r۲) باشد، فرمول محاسبه لختی دورانی آن به فرم زیر درمیآید:
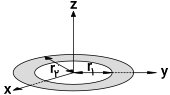
اگر چگالی سطح (جرم در واحد سطح) برای حلقه بالا، یک عدد ثابت باشد، لختی دورانی آن توسط روابط زیر محاسبه میشود:
π، عدد ثابت ۳/۱۴ و ، چگالی سطح را نمایش میدهد.
ممان اینرسی دیسک توپر چیست ؟
دیسک توپر به شعاع r و جرم m را در نظر بگیرید.
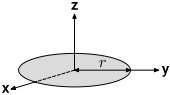
فرمول ممان اینرسی دیسک بالا، حول محورهای دستگاه مختصات سهبعدی به صورت زیر نوشته میشود:
دیسک توپر، یک حالت خاص از استوانه توپر با ارتفاع صفر (h = ۰) است. ممانهای اینرسی حول سه محور، به صورت زیر با یکدیگر رابطه دارند:
به عبارت دیگر، ممان اینرسی حول محور Z، دو برابر همین ممان حول محورهای X و Y است. این ویژگی، از قضیه محورهای عمود نشات میگیرد.
ممان اینرسی استوانه توخالی چیست ؟
تصویر زیر، یک پوسته استوانهای نازک با دو انتهای باز را نمایش میدهد. شعاع این استوانه برابر با r و جرم آن برابر با m است.
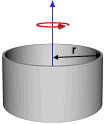
ممان اینرسی استوانه بالا، از رابطه زیر به دست میآید:
جواب فرمول بالا، به صورت تقریبی است؛ چراکه در آن از ضخامت استوانه صرفنظر میشود. این استوانه، حالت خاصی از لوله با شعاع داخلی و خارجی برابر (r۱=r۲) است. ممان اینرسی جرم نقطهای m در انتهای میلهای به طول r نیز توسط رابطه بالا تعیین میشود. در این حالت، به r، شعاع ژیراسیون میگویند.
ممان اینرسی استوانه توپر چیست ؟
لختی دورانی استوانه توپر به شعاع r، ارتفاع h و جرم m، برابر است با:
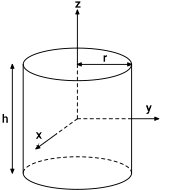
استوانه توپر را میتوان به عنوان حالت خاصی از لوله با شعاع داخلی صفر (r۱=۰) در نظر گرفت.
ممان اینرسی لوله استوانه ای با جداره ضخیم چیست ؟
یک لوله استوانهای با جداره ضخیم را در نظر بگیرید. این لوله، دارای شعاع داخلی r۱، شعاع خارجی r۲ و ارتفاع h است.
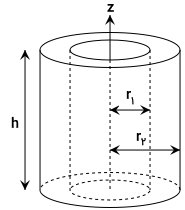
اگر جرم لوله بالا برابر با m باشد، لختی دورانی آن حول محور Z برابر با رابطه زیر خواهد بود:
t، از فرمول زیر به دست میآید:
این پارامتر، نسبت ضخامت نرمالشده را نمایش میدهد. لختی دورانی لوله حول محورهای X و Y، عبارت است از:
فرمول بالا، لختی دورانی حول صفحه xy گذرنده از مرکز جرم لوله است. اگر این صفحه در کف لوله قرار داشته باشد (در )، بر اساس قضیه محورهای موازی، ممان اینرسی برابر با رابطه زیر خواهد بود:
در صورت یکسان بودن هندسه و چگالی سطح (ρ)، روابط لختی دورانی به فرم زیر نوشته میشوند:
ممان اینرسی هرم مثلثی چیست ؟
تصویر زیر، یک هرم با قاعده و وجههای مثلثی (مثلث متساویالاضلاع) را نمایش میدهد. این هرم، یک چهاروجهی منتظم با ضلعهایی به اندازه s و جرم m است.
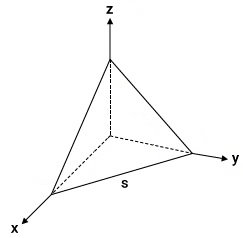
در صورت توپر بودن هرم بالا، لختی دورانی آن مطابق با فرمول زیر محاسبه میشود:
اگر هرم، توخالی باشد، محاسبه لختی دورانی آن بر اساس رابطه زیر انجام میگیرد:
ممان اینرسی کره توخالی چیست ؟
کره توخالی به جرم m و شعاع r را در نظر بگیرید.
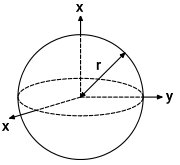
محاسبه لختی دورانی کره توخالی بالا از فرمول زیر به دست میآید:
ممان اینرسی کره توپر چیست ؟
تصویر زیر، یک کره توپر به شعاع r و جرم m را نمایش میدهد.
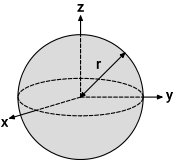
لختی دورانی کره توپر بالا توسط فرمول زیر محاسبه میشود:
ممان اینرسی پوسته کروی دارای ضخامت چیست ؟
یک پوسته کروی با ضخامت مشخص، شعاع داخلی r۱، شعاع خارجی r۲ و جرم m را در نظر بگیرید.
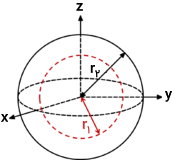
لختی دورانی کره دارای جداره ضخیم (ضخامت غیر قابل چشمپوشی)، توسط رابطه زیر تعیین میشود:
اگر شعاع داخلی کره برابر با صفر باشد (r۱=۰)، یک کره توپر به وجود میآید. در صورتی که شعاع داخلی با شعاع خارجی برابر باشد (r۱=r۲)، کره توپر به عنوان یک پوسته کروی توخالی در نظر گرفته میشود.
ممان اینرسی مخروط توپر و توخالی چیست ؟
تصویر زیر، یک مخروط قائم با شعاع r و ارتفاع h را نمایش میدهد.
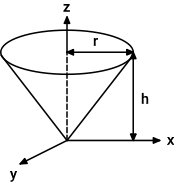
اگر مخروط بالا، توپر باشد، میتوانیم سه حالت را در نظر بگیریم. در تمام حالتها، فرمول لختی دورانی مخروط توپر حول محور Z برابر است با:
در حالت اول، راس مخروط به عنوان محور دوران در نظر گرفته میشود. در این حالت، ممانهای اینرسی حول محورهای X و Y، از رابطه زیر به دست میآید:
در حالت دوم، محور دوران از درون قاعده گذر میکند. فرمول لختی دورانی برای این حالت به صورت زیر نوشته میشود:
در حالت سوم، محور دوران از مرکز جرم مخروط میگذرد. برای این حالت، فرمول ممان اینرسی عبارت است از:
اگر مخروط، توخالی باشد، لختی دورانی حول محورهای سهگانه از روابط زیر به دست میآید:
ممان اینرسی صفحه مستطیلی شکل چیست ؟
تصویر زیر، یک صفحه مستطیلی شکل به طول h، عرض w و جرم m را نمایش میدهد.
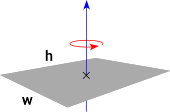
اگر محور دوران، مانند تصویر بالا، از مرکز صفحه عبور کند، فرمول لختی دورانی به صورت زیر نوشته میشود:
اکنون محور دوران را به انتهای صفحه انتقال در نظر بگیرید.
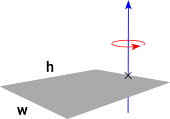
لختی دورانی صفحه مستطیلی بالا از رابطه زیر به دست میآید:
ممان اینرسی مکعب مستطیل توپر چیست ؟
مکعب مستطیل توپر زیر، دارای طول h، عرض w، ارتفاع d و جرم m است.
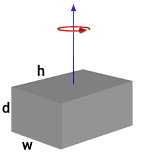
لختی دورانی مکعب مستطیل بالا، در راستای محورهای عمودی گذرنده از وجههای آن عبارت است از:
مکعب مربع، یکی از حالتهای خاص مکعب مستطیل است که در آن، تمام لبهها، اندازه برابر دارند. فرمول لختی دورانی مکعب مربع حول محور مرکزی، از رابطه زیر به دست میآید:
اگر محور دوران از قطر بزرگ مستطیل عبور کند، فرمول ممان اینرسی به صورت زیر نوشته میشود:
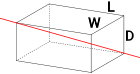
در مکعب مربع، فرمول لختی دورانی حول قطر از رابطه زیر به دست میآید:
ممان اینرسی چند ضلعی منتظم چیست ؟
چندضلعی منتظم، از n ضلع با اندازههای برابر تشکیل میشود. علاوه بر این، این نوع چندضلعی، n زاویه داخلی مساوی دارد.
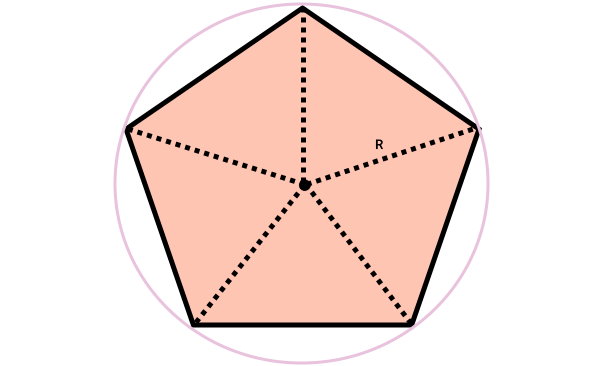
اگر شعاع دایره محیط بر چندضلعی منتظم برابر با R و وزن چندضلعی منتظم برابر با m باشد، لختی دورانی حول محور گذرنده از مرکز جرم، توسط رابطه زیر تعیین میشود:
جدول ممان اینرسی اشکال هندسی
در بخش قبلی، روابط مربوط به محاسبه ممان اینرسی شکلهای مهم و پرکاربرد را معرفی کردیم. جدول زیر، خلاصهای از این روابط را به همراه چند رابطه دیگر نمایش میدهد.
| شکل | فرمول ممان اینرسی | پارامترها |
| یک نقطه | M: جرم نقطهای؛ r: کمترین فاصله جرم تا محور دوران | |
| دو نقطه | m۱: جرم نقطه اول؛ m۲: جرم نقطه دوم؛ μ: جرم کاهشیافته؛ x: فاصله بین دو نقطه | |
| میله | Ic: ممان اینرسی حول محور گذرنده از مرکز جرم؛ m: جرم میله؛ L: طول میله | |
| Ie: ممان اینرسی حول محور گذرنده از انتهای میله؛ m: جرم میله؛ L: طول میله | ||
| دیسک توپر |
| Iz: ممان اینرسی حول محور Z؛ Ix: ممان اینرسی حول محور X؛ Iy: ممان اینرسی حول محور Y؛ m: جرم دیسک؛ r: شعاع دیسک |
| حلقه دارای ضخامت |
| Iz: ممان اینرسی حول محور Z؛ Ix: ممان اینرسی حول محور X؛ Iy: ممان اینرسی حول محور Y؛ m: جرم حلقه؛ r۱: شعاع داخلی حلقه؛ r۲: شعاع خارجی حلقه |
| حلقه توخالی |
| Iz: ممان اینرسی حول محور Z؛ Ix: ممان اینرسی حول محور X؛ Iy: ممان اینرسی حول محور Y؛ m: جرم حلقه؛ r: شعاع حلقه |
| مستطیل مسطح | Ic: ممان اینرسی حول محور گذرنده از مرکز مستطیل؛ m: جرم مستطیل؛ h: طول مستطیل؛ w: عرض مستطیل | |
| Ie: ممان اینرسی حول محور گذرنده از انتهای مستطیل؛ m: جرم مستطیل؛ h: طول مستطیل؛ w: عرض مستطیل | ||
| چندضلعی منتظم مسطح | m: جرم صفحه؛ R: شعاع دایره محیط بر چندضلعی؛ n: تعداد ضلعهای چندضلعی | |
| مکعب مستطیل توپر |
| Ih: ممان اینرسی حول محور گذرنده از مرکز وجه طولی؛ Iw: ممان اینرسی حول محور گذرنده از مرکز وجه عرضی؛ Id: ممان اینرسی حول محور گذرنده از مرکز وجه ارتفاعی؛ m: جرم مکعب مستطیل |
|
(محور قطری) | L: طول مکعب مستطیل؛ W: عرض مکعب مستطیل؛ D: ارتفاع مکعب مستطیل؛ m: جرم مکعب مستطیل | |
| مکعب مربع توپر | ICM: ممان اینرسی حول محور گذرنده از مرکز وجوه؛ m: جرم مکعب مربع؛ s: اندازه ضلعهای مکعب مربع | |
|
(محور قطری) | m: جرم مکعب مربع؛ s: اندازه ضلعهای مکعب مربع | |
| استوانه توپر |
| Iz: ممان اینرسی حول محور Z؛ Ix: ممان اینرسی حول محور X؛ Iy: ممان اینرسی حول محور Y؛ m: جرم استوانه؛ r: شعاع مقطع استوانه؛ h: ارتفاع استوانه |
| استوانه دارای جداره ضخیم |
| Iz: ممان اینرسی حول محور Z؛ Ix: ممان اینرسی حول محور X؛ Iy: ممان اینرسی حول محور Y؛ m: جرم استوانه؛ r۱: شعاع داخلی استوانه؛ r۲: شعاع خارجی استوانه؛ h: ارتفاع استوانه |
|
؛ (محور انتهایی) | ||
| استوانه دارای جداره نازک | m: جرم استوانه؛ r: شعاع مقطع استوانه | |
| چهاروجهی منتظم توپر | m: جرم چهاروجهی؛ s: اندازه ضلع | |
| چهاروجهی منتظم توخالی | ||
| کره توپر | m: جرم کره؛ r: شعاع کره | |
| کره با جداره ضخیم | m: جرم کره؛ r۱: شعاع داخلی کره؛ r۲: شعاع خارجی کره | |
| کره با جداره نازک | m: جرم کره؛ r: شعاع کره | |
| بیضیگون |
| Ia: ممان اینرسی حول محور طولی؛ Ib: ممان اینرسی حول محور عرضی؛ Ic: ممان اینرسی حول محور ارتفاعی؛ a: طول یا بیشتر گسترش طولی بیضیگون؛ b: عرض یا کمترین گسترش بیضیگون؛ c: ارتفاع یا بیشترین گسترش بیضیگون در بعد سوم؛ m: جرم بیضیگون |
| مخروط توپر | m: جرم مخروط؛ r: شعاع قاعده مخروط | |
|
(محور راس) | m: جرم مخروط؛ r: شعاع قاعده مخروط؛ h: ارتفاع مخروط | |
|
(محور قاعده) | ||
|
(محور مرکز جرم) | ||
| مخروط توخالی |
| m: جرم مخروط؛ r: شعاع قاعده مخروط؛ h: ارتفاع مخروط |
| چنبره |
(محور مرکزی) | m: جرم چنبره؛ a: شعاع کوچک چنبره؛ b: شعاع بزرگ چنبره |
|
(محور قطری) |
تفاوت گشتاور دوم سطح با ممان اینرسی
به دلیل شباهتهای زیاد بین فرمول ممان اینرسی با گشتاور دوم سطح و شباهت اسمی بین این دو (گشتاور دوم جرم و گشتاور دوم سطح)، امکان اشتباه در تعریف و استفاده کمیتهای مذکور وجود دارد. در جدول زیر، تفاوتهای اصلی این کمیتها آورده شدهاند.
| معیار مقایسه | ممان اینرسی جرم | گشتاور دوم سطح |
| فرمول | ||
| واحد بینالمللی | ||
| مفهوم | توزیع جرم جسم نسبت به محور دلخواه | مقاومت در برابر تغییر شتاب زاویهای حول محور دلخواه |
| کاربرد | مسائل دینامیکی | مسائل مقاومت مصالح (خمش تیر) یا مسائل مکانیک مواد |
برای یادگیری کامل مفهوم ممان اینرسی، باید با مفاهیم پارامترهای مقاومت مصالح آشنا باشید. مطالعه مطلب «مقاومت مصالح چیست؟ – پارامترها و مفاهیم پایه به زبان ساده» به شما کمک میکند تا به درک بهتری از خصوصیات رفتاری مواد برسید.
محاسبه آنلاین ممان اینرسی
ابزارهای اینترنتی مختلفی برای محاسبه ممان اینرسی وجود دارند. یکی از این ابزارها، ماشین حساب سایت OmniCalculator (+) است. تصویر زیر، نمایی از ماشینحساب ممان اینرسی (گشتاور دوم جرم) برای اشکال معروف هندسی را نمایش میدهد.
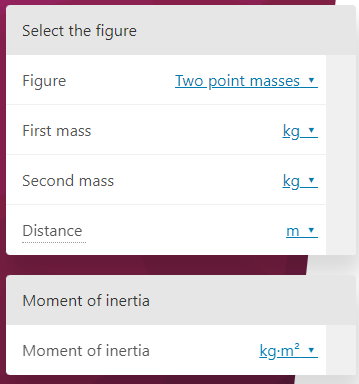
در کادر مقابل عنوان «Figure»، امکان انتخاب شکل مورد نظر فراهم شده است.
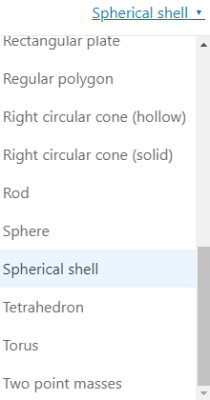
به عنوان مثال، اگر گزینه «Spherical Shell» را از بخش مذکور انتخاب کنیم، کادرهای مربوط به وارد کردن پارامترهای محاسبه ممان اینرسی پوسته کروی (جرم، شعاع داخلی و شعاع خارجی) به نمایش درمیآیند.
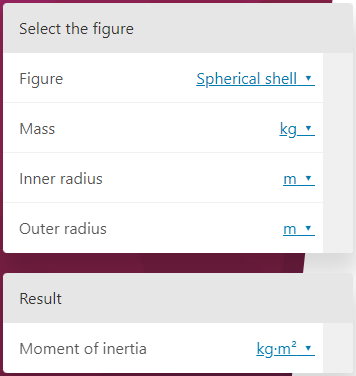
با وارد کردن مقادیر مورد نظر، نتیجه ممان اینرسی در کادر مقابل «Moment of Inertia» نشان داد میشود.
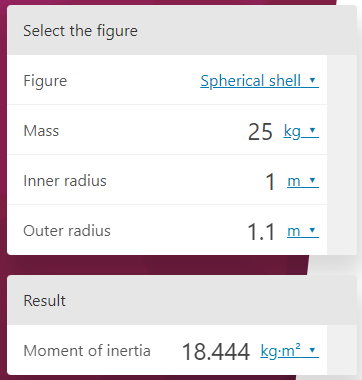
در صورت تمایل میتوانید یکای هر یک از پارامترهای ورودی و خروجی مورد نظر را تغییر دهید.
سوالات متداول در رابطه با ممان اینرسی
در این بخش، به برخی از پرتکرارترین سوالات در رابطه با ممان اینرسی به طور خلاصه پاسخ میدهیم.
تعریف ممان اینرسی یعنی چه ؟
ممان اینرسی، مقاومت ذرات جسمِ در حال حرکت دورانی، در برابر شتاب زاویهای است.
نام دیگر ممان اینرسی چیست ؟
ممان اینرسی، با عنوان «لختی دورانی» و «گشتاور دوم جرم» نیز شناخته میشود.
منشا وجود ممان اینرسی چیست ؟
جرم جسم، دلیل وجود ممان اینرسی و مقاومت آن در برابر شتاب زاویهای است.
رابطه ممان اینرسی با جرم جسم چگونه است ؟
ممان اینرسی با جرم جسم، رابطه مستقیم دارد. هرچه جرم بیشتر باشد، این پارامتر (مقاومت در برابر شتاب زاویهای) نیز بیشتر میشود.
یکای ممان اینرسی چیست ؟
واحد ممان اینرسی در سیستم بینالمللی (SI)، کیلوگرم در متر مربع است. در سیستمهای دیگر، یکای این کمیت، به صورت حاصلضرب جرم در مربع طول بیان میشود.
دلیل نامگذاری ممان اینرسی چیست ؟
ممان اینرسی، از دو کلمه «ممان» به معنای گشتاور یا نیروی دورانی و «اینرسی» به معنای لختی یا مقاومت در برابر تغییر حالت تشکیل میشود. این دو کلمه، ماهیت ممان اینرسی (نیروی دورانی مورد نیاز برای غلبه بر حالت جسم در حرکت دورانی) را نمایش میدهد.
آیا ممان اینرسی یک کمیت تانسور است ؟
بله. ممان اینرسی، هم دارای مقدار و هم دارای جهت است؛ اما از اصول محاسبات بردارها پیروی نمیکند. به این ترتیب، این کمیت، به عنوان یک کمیت تانسور در نظر گرفته میشود.
ممان اینرسی چگونه بدست می آید ؟
ممان اینرسی، از مجموع یا انتگرال حاصلضرب جرمهای جزئی جسم در مربع فاصله آنها تا یک محور مشخص به دست میآید.
علامت ممان اینرسی چیست ؟
رایجترین و شناخته شدهترین علامت برای نمایش ممان اینرسی، حرف I است.
فرمول ممان اینرسی چیست ؟
فرمول انتگرالی ممان اینرسی به فرم I=∫r۲dm نوشته میشود. r، فاصله هر بخش از جرم m یا همان dm از محور مورد نظر را نمایش میدهد.
ممان اینرسی در کجا کاربرد دارد ؟
ممان اینرسی، در خودروسازی، هواپیماسازی، کشتیسازی، مکانیک و عمران کاربرد دارد. قطعاتی نظیر فلایویل، شفتها، تیرها و غیره، با کمک مفهوم لختی دورانی طراحی میشوند.
آزمون سنجش یادگیری
۱. کدام جمله بهترین توصیف برای ممان اینرسی (لختی دورانی) است و ارتباط آن با مقاومت جسم نسبت به تغییر حرکت دورانی را بیان میکند؟
ممان اینرسی نشانه میزان مقاومت جسم در برابر آغاز یا توقف چرخش به دلیل جرم و فاصله اجزا تا محور دوران است.
ممان اینرسی تنها در حرکت خطی نقش دارد و در حرکت دورانی تاثیری ندارد.
ممان اینرسی نشاندهنده مجموع نیروهای وارد بر جسم است.
ممان اینرسی فقط به جنس ماده بستگی دارد و مقدار آن برای همه اجسام یکسان است.
عبارت «ممان اینرسی نشانه میزان مقاومت جسم در برابر آغاز یا توقف چرخش به دلیل جرم و فاصله اجزا تا محور دوران است» توضیح میدهد که این کمیت وابستگی به جرم و چگونگی توزیع آن نسبت به محور دارد و به همین دلیل در شروع یا توقف حرکت چرخشی جسم، مقاومت زیادی ایجاد میکند. گزینه «مجموع نیروهای وارد بر جسم» تعریف گشتاور یا نیرو است نه ممان اینرسی. جمله مربوط به وابستگی تنها به جنس ماده نادرست است، زیرا فاصله اجزا تا محور موثر است. همچنین عبارت «ممان اینرسی تنها در حرکت خطی نقش دارد» نادرست است، چون این کمیت مخصوص حرکت دورانی است.
۲. در محاسبه گشتاور (Moment/Torque)، کدام عوامل از میان موارد زیر نقش مستقیم دارند و هر یک چگونه بر مقدار گشتاور تاثیرگذارند؟
نیرو، فاصله تا محور و زاویه بین آنها تاثیر یکسان دارند.
تنها نیروی وارد شده تعیینکننده گشتاور است.
گشتاور فقط به جرم جسم بستگی دارد.
نیرو، فاصله از محور و زاویه اثر، هر سه بر مقدار گشتاور موثرند.
گشتاور (Moment/Torque) وابسته به نیرو، فاصله از محور دوران و زاویهی اثر نیرو با محور است. هر سه پارامتر باعث تغییر مقدار گشتاور میشوند، یعنی افزایش نیرو یا فاصله یا افزایش مولفه عمودی نیرو نسبت به محور، باعث افزایش گشتاور میگردد. عبارت «نیرو، فاصله تا محور و زاویه بین آنها تاثیر یکسان دارند» نادرست است چون نقش هر کدام متفاوت است و زوایا تاثیر سینوسی دارند. تمرکز صرف بر نیرو یا جرم نیز نادرست است، چون فرمول گشتاور به این سه پارامتر نیاز دارد.
۳. فرمول کلی گشتاور چگونه نوشته میشود و زاویه نیرو چه تاثیری بر مقدار گشتاور دارد؟
گشتاور همواره برابر با حاصل ضرب ساده نیرو و فاصله است.
فرمول گشتاور به صورت حاصل ضرب نیرو و فاصله و سینوس زاویه آنها بیان میشود.
فرمول گشتاور حاصل جمع نیروهای وارد بر جسم است و زاویه اثری ندارد.
فرمول گشتاور فقط برای نیروهای عمود بر بازو تعریف شده و زاویه اهمیتی ندارد.
گشتاور با فرمول M = F · d · sin(α) تعریف میشود که در آن F نیرو، d فاصله تا محور چرخش و α زاویه بین نیرو و بازو است. بسته به مقدار سینوس زاویه، تاثیر نیرو بر گشتاور تغییر میکند؛ اگر زاویه صفر باشد گشتاور صفر میشود و بیشترین مقدار آن زمانی است که نیرو عمود بر بازو وارد شود. انتخابهایی که زاویه را بیتاثیر یا صرفا حاصل ضرب مستقیم نیرو و فاصله میدانند نادرست هستند، زیرا نقش زاویه را نادیده میگیرند.
۴. در مهندسی، تمایز اصلی بین کاربردهای گشتاور اول سطح و گشتاور اول جرم در چیست؟
هر دو عمدتا در طراحی سازههای لوکس و معماری تزئینی کاربرد دارند.
گشتاور اول سطح برای یافتن مرکز هندسی و گشتاور اول جرم برای محاسبات مبتنی بر جرم به کار میرود.
گشتاور اول سطح اغلب برای محاسبه اینرسی دورانی و گشتاور اول جرم برای سختی مصالح استفاده میشود.
گشتاور اول جرم تنها در علوم پایه و گشتاور اول سطح فقط در هوافضا کاربرد دارد.
در کاربردهای مهندسی، «گشتاور اول سطح» جهت تعیین مرکز هندسی یا مرکز سطح استفاده میشود، در حالی که «گشتاور اول جرم» بر پایه جرم سیستم است و برای تحلیلهای مبتنی بر جرم کاربرد دارد. گزینهای که اشاره به همین کاربردها دارد درست است، زیرا دیگر گزینهها این تمایز را به درستی بیان نمیکنند یا اطلاعات نادرست ارائه میدهند.
۵. گشتاور دوم سطح در مهندسی چه کاربردی دارد و فرمول انتگرالی آن چگونه بیان میشود؟
برای محاسبه مقاومت کششی یک ماده به کار میرود و فرمول آن I = ∫σ dA است.
برای تعیین مرکز جرم جسمی مورد استفاده قرار میگیرد و فرمول آن I = ∫xdA است.
برای سنجش نحوه توزیع سطح نسبت به یک محور به کار میرود و با انتگرال I = ∫y² dA تعریف میگردد.
برای اندازهگیری مقدار جرم یک جسم و انتگرال آن I = ∫dm میباشد.
گشتاور دوم سطح، مشخصهای هندسی است که برای نمایش نحوه توزیع سطوح نسبت به یک محور استفاده میشود و فرمول اصلی آن به صورت انتگرالی I = ∫y² dA بیان میگردد. عبارت «تعیین مرکز جرم» مربوط به گشتاور اول سطح است. عبارت «اندازهگیری مقدار جرم» ارتباطی با گشتاور دوم سطح ندارد و به جرم کل اشاره دارد. عبارت «محاسبه مقاومت کششی» نیز به گشتاور دوم سطح مربوط نیست و به ویژگیهای مکانیکی ماده اشاره میکند.
۶. کدام گزینه درباره ارتباط جرم (Mass) و اینرسی (Inertia) صحیح است؟
افزایش جرم باعث افزایش اینرسی میشود.
اینرسی جسم تنها به شکل هندسی آن وابسته است.
هرچه جرم کمتر باشد، اینرسی بیشتر خواهد بود.
جرم تاثیری بر مقدار اینرسی ندارد.
عبارت «افزایش جرم باعث افزایش اینرسی میشود» درست است چون اینرسی (Inertia) یا لختی یک جسم مستقیما با مقدار جرم آن ارتباط دارد؛ اگر جرم جسم بیشتر باشد، مقاومت آن در برابر تغییر حالت سکون یا حرکت نیز بیشتر است. جمله «هرچه جرم کمتر باشد، اینرسی بیشتر خواهد بود» صحیح نیست چون کاهش جرم موجب کاهش اینرسی میگردد. اینکه «اینرسی تنها به شکل هندسی وابسته است» نادرست است، چرا که جرم نیز در تعیین آن نقش دارد. همچنین «جرم تاثیری بر مقدار اینرسی ندارد» غلط بوده، زیرا جرم عامل اصلی تعیینکننده اینرسی است.
۷. ممان اینرسی (Moment of Inertia) یک جسم در حرکت زاویهای چه مفهومی را بیان میکند و شتاب زاویهای چه تاثیری بر آن دارد؟
ممان اینرسی مقدار نیروی لازم برای حرکت خطی جسم را تعیین میکند و شتاب زاویهای آن را تغییر نمیدهد.
این پارامتر نشاندهنده مقاومت جسم در برابر تغییر سرعت زاویهای است و با افزایش شتاب زاویهای، مقدار آن تغییر نمیکند.
این کمیت فقط برای اجسام با جرم ثابت استفاده میشود و اثری از شتاب زاویهای در آن دیده نمیشود.
ممان اینرسی نسبت بین شتاب زاویهای و سرعت خطی را بیان میکند و با افزایش شتاب زاویهای کاهش مییابد.
ممان اینرسی نشاندهنده مقاومت جسم در برابر تغییر شتاب زاویهای یا همان لختی دورانی است و مستقل از مقدار شتاب زاویهای، ثابت میماند؛ یعنی وقتی شتاب زاویهای افزایش مییابد، مقدار ممان اینرسی به خاطر مشخصات جرم و موقعیت وضعیت جسم تغییر نمیکند. «مقدار نیروی لازم برای حرکت خطی» و «نسبت بین شتاب زاویهای و سرعت خطی» ویژگیهای مربوط به کمیتهای دیگر هستند و ارتباط مستقیمی با تعریف ممان اینرسی ندارند. همچنین ممان اینرسی تنها وابسته به توزیع جرم و فاصله تا محور دوران است و برای هر جسم فارغ از مقدار شتاب زاویهای معنا دارد.
۸. در فرمولبندی ممان اینرسی (Moment of Inertia) برای دستگاههای گسسته و پیوسته، اصلیترین تفاوت در کدام بخش محاسباتی دیده میشود؟
در دستگاههای گسسته فاصله از محور نادیده گرفته میشود ولی در پیوسته لحاظ میگردد.
در هر دو حالت فقط مقدار کل جرم ملاک است و نحوه بیان فرمول تفاوتی ندارد.
در دستگاههای گسسته از مجموع مقادیر جرم و فاصله استفاده میشود، در پیوسته از انتگرال برای جرمهای بینهایت کوچک
فرمول دستگاههای پیوسته فقط برای اجسام با شکل کروی کاربرد دارد ولی گسسته برای هر جسمی به کار میرود.
در محاسبه ممان اینرسی برای دستگاههای گسسته، جرم هر ذره جداگانه و فاصله آن نسبت به محور به صورت مجموع Σ(mᵢ rᵢ²) لحاظ میشود. اما برای دستگاههای پیوسته، به دلیل بینهایت بودن ذرات، از انتگرال ∫r²dm برای درنظر گرفتن توزیع پیوسته جرم استفاده میکنند. برخلاف پاسخهایی مانند «فقط مقدار کل جرم ملاک است» یا «فرمول پیوسته فقط برای شکل کروی است»، همواره ساختار محاسبه بر مبنای مجموع یا انتگرال است. همچنین فاصله از محور همیشه مهم است و نادیده گرفته نمیشود.
۹. چرا محاسبه ممان اینرسی در طراحی سازههای مهندسی اهمیت دارد؟
صرفا برای زیباسازی ظاهر سازه
برای تعیین پایداری و تعادل قطعات سازه
تنها برای انتخاب جنس مواد سازه
برای کاهش هزینه ساخت سازه
محاسبه ممان اینرسی به این دلیل اهمیت دارد که امکان ارزیابی پایداری، تعادل و رفتار دینامیکی قطعات سازه تحت نیروهای مختلف را مهیا میکند. به کمک این پارامتر، مهندسان میتوانند شتابدهی، میزان نیروی لازم و کارایی قطعات را در طراحی بهینهسازی کنند. پاسخهایی چون «تنها برای انتخاب جنس مواد سازه» یا «زیباسازی ظاهر سازه» به کاربرد عملی و اساسی ممان اینرسی مربوط نمیشوند و «کاهش هزینه ساخت سازه» نیز هدف اصلی استفاده از این پارامتر نیست؛ بلکه بهبود عملکرد و تعادل ساختار مد نظر است.
۱۰. در محاسبه ممان اینرسی برای سیستمی از چند ذره نقطهای، کدام روش نتیجه دقیقتری میدهد؟
استفاده از مجموع m·r برای هر ذره نسبت به محور
استفاده از فرمول ممان اینرسی مخصوص میلهها
محاسبه انتگرال سطحی برای توزیع صفحهای
جمع کردن حاصل ضرب جرم هر ذره در مربع فاصلهاش از محور
برای سیستمی از چند ذره نقطهای، مناسبترین روش جمع کردن حاصل ضرب جرم هر ذره در مربع فاصلهاش از محور است؛ یعنی همان رابطه I = Σ(mᵢrᵢ²) که طبق متن برای این موارد پیشنهاد شده است. روشهایی مانند استفاده از مجموع m·r یا انتگرال سطحی برای سیستم پیوسته یا اشکال هندسی خاص به کار میروند و برای ذرات نقطهای نتیجه دقیق نمیدهند. همچنین فرمول ممان اینرسی مخصوص میلهها برای اجسام پیوسته و یکدست است، نه چند ذره مجزا.
۱۱. قضیه محورهای موازی چگونه به محاسبه ممان اینرسی کمک میکند و کاربرد اصلی آن چیست؟
این قضیه صرفا در مسائل الکتریکی کاربرد دارد.
این قضیه فقط برای اجسام توخالی کاربرد دارد.
تنها برای محاسبه مرکز جرم به کار میرود.
با استفاده از آن میتوان ممان اینرسی را حول محوری غیر از محور مرکز جرم به دست آورد.
قضیه محورهای موازی اجازه میدهد با دانستن ممان اینرسی نسبت به محور مرکز جرم، مقدار ممان اینرسی نسبت به هر محور موازی را محاسبه کرد. عبارت «با استفاده از آن میتوان ممان اینرسی را حول محوری غیر از محور مرکز جرم به دست آورد» توصیف دقیقی از کاربرد این قضیه است. کاربرد این قانون محدود به اجسام توخالی یا مسائل الکتریکی نیست و فقط برای یافتن مرکز جرم به کار نمیرود.
۱۲. در تعیین ممان اینرسی یک میله استوانهای نسبت به دو محور مختلف، چگونه میتوان از انتگرال و قضیه محورهای موازی بهره برد؟
مستقیما فرمول گشتاور دوم سطح را استفاده میکنیم و نیازی به انتگرال نیست.
محاسبه تنها با تقسیم طول میله بر شعاع آن انجام میشود و محورهای موازی اثری ندارند.
برای تمامی محورها فقط جرم را در شتاب زاویهای ضرب میکنیم و نقش انتگرال حذف میشود.
ابتدا انتگرال ممان اینرسی نسبت به مرکز جرم حساب شده و سپس با استفاده از جرم و فاصله تا محور جدید، مقدار نهایی به دست میآید.
برای محاسبه ممان اینرسی میله استوانهای نسبت به محور مرکز جرم ابتدا باید از طریق انتگرالگیری مقدار آن را به دست آورد و بعد اگر محور مورد نظر موازی و خارج از مرکز جرم باشد، با استفاده از جرم میله و مربع فاصله بین دو محور طبق قضیه محورهای موازی مقدار نهایی محاسبه میشود. فرمول گشتاور دوم سطح بدون انتگرال برای این حالت کافی نیست و تقسیم طول بر شعاع یا ضرب جرم در شتاب زاویهای روشهای صحیحی برای این محاسبه نیستند.
۱۳. هنگام انتخاب فرمول مناسب برای محاسبه ممان اینرسی (Moment of Inertia) یک شکل هندسی ساده مانند میله یا دیسک، چه عواملی باید مورد توجه قرار گیرد؟
شکل هندسی و محل محور دوران نسبت به جسم
تعداد ذرات سازنده بدون توجه به فاصله آنها
نوع ماده سازنده و سطح تماس با زمین
جرم کل جسم بدون توجه به هندسه
انتخاب صحیح فرمول ممان اینرسی بستگی به 'شکل هندسی و محل محور دوران نسبت به جسم' دارد، زیرا هر فرمول با فرضهای خاصی برای هندسه و محور مورد نظر نوشته شده است. فرمولهای مختلف برای مثلا میله با محور وسط، میله با محور انتهایی، دیسک یا حلقه وجود دارد و تحلیل غلطِ محور یا شکل موجب خطا میشود. عواملی مانند 'جرم کل بدون توجه به هندسه'، 'نوع ماده سازنده و سطح تماس با زمین' یا صرفا 'تعداد ذرات بدون توجه به فاصله' به تنهایی تعیینکننده فرمول صحیح نیستند، زیرا توزیع جرم نسبت به محور دوران عاملی کلیدی است که فقط از ترکیب هندسه و محل محور به دست میآید.
۱۴. چرا هنگام انتخاب فرمول ممان اینرسی (Moment of Inertia) برای اشکالی مانند حلقه یا کره باید به پارامترهای هندسی آنها توجه ویژه داشت؟
چون پارامترهای هندسی تعیین میکنند کدام فرمول و کدام محور دوران بهکار میرود
چون پارامترهای هندسی فقط واحد اندازهگیری را تعیین میکنند و بر مقدار تاثیری ندارد
زیرا فرمول برای همه شکلها یکسان است و فقط نماد متفاوت دارد
زیرا همه فرمولهای ممان اینرسی صرفا به جرم وابسته هستند و نیازی به شکل هندسی ندارند
در محاسبه ممان اینرسی برای اشکال ویژه مثل حلقه یا کره، پارامترهای هندسی مانند شعاع، طول یا ضخامت تعیین میکنند که کدام فرمول و حول کدام محور باید استفاده شود. شکل و ابعاد یک جسم مستقیم بر توزیع جرم نسبت به محور دوران تاثیر دارد و فرمولها بر اساس این تفاوتها تدوین شدهاند. گزینههایی مانند تکیه صرف بر جرم یا استفاده از یک فرمول برای همه اجسام، نادرستاند زیرا هر هندسه فرمول اختصاصی مُتناسب با پارامترهایش دارد. تعیین فقط واحد اندازهگیری نیز بر نتیجهی عددی تاثیرگذار نیست و انتخاب فرمول را مشخص نمیکند؛ بلکه شکل هندسی و مشخصات آن راهنمای اصلی هستند.
۱۵. در مقایسه میان گشتاور دوم سطح و ممان اینرسی جرم، تفاوت عمده در چه جنبههایی مشاهده میشود؟
هر دو برای تعیین شتاب translational استفاده میشوند و واحدشان نیوتن-متر است.
گشتاور دوم سطح و ممان اینرسی تفاوتی در مفهوم و فرمول ندارند.
ممان اینرسی جرم تنها برای اجسام جامد بهکار میرود و برحسب متر محاسبه میشود.
گشتاور دوم سطح در مقاومت مصالح کاربرد دارد و واحد آن متر به توان چهار است.
عبارت «گشتاور دوم سطح در مقاومت مصالح کاربرد دارد و واحد آن متر به توان چهار است» صحیح است؛ طبق مطالب ارائهشده، گشتاور دوم سطح برای آنالیز مقاومت اجسام و محاسبات مصالح به کار میرود و واحد آن m⁴ میباشد. سایر گزینهها نادرستاند؛ عبارت «برای تعیین شتاب translational» و واحد نیوتن-متر ربطی به این کمیتها ندارد، ممان اینرسی جرم در دینامیک اجسام جامد و حتی ذرات نقطهای تعریف میشود و واحد آن kg·m² است، و مفاهیم و فرمولهای این دو کمیت بر اساس کاربرد و پارامتر متفاوتاند و یکسان نیستند.
۱۶. در مهندسی سازه، ممان اینرسی چگونه به پایداری و عملکرد سازهها کمک میکند؟
مقدار نیروی برشی را افزایش میدهد.
مقاومت سازه در برابر شتاب زاویهای را افزایش میدهد.
سازه را نسبت به تغییرات دمایی حساستر میکند.
باعث کاهش وزن کلی سازه میشود.
عبارت «مقاومت سازه در برابر شتاب زاویهای را افزایش میدهد» صحیح است زیرا در توضیح اهمیت ممان اینرسی ذکر شده که این پارامتر مشخص کننده مقاومت اجسام و سازهها در برابر تغییر وضعیت حرکتی یا اعمال شتاب زاویهای است و نقش کلیدی در تحلیل و طراحی پایداری سازهها دارد. کاهش وزن کلی یا افزایش نیروی برشی رابطهای با ممان اینرسی ندارند و حساسیت به دما ارتباطی به این پارامتر ندارد.













بسیار عالی و آموزنده
توضیحات علمی،تخصصی اما قابل درک
با سلام و درود فراوان
من فقط یک موردش را هضم نکردم این بود که چرا باید r مربع باشد یعنی در فرمول r چرا باید به توان دو برسد ؟
با تشکر از مطالب مفید و با ارزشتون
با سلام خدمت شما؛
اگر به تصویر ابتدای بخش «لختی دورانی یا ممان اینرسی چیست؟» دقت کنید، برای محاسبه ممان اینرسی حول یک نقطه مشخص یک دایره فرضی رسم شده است. در واقع ممان اینرسی به نوعی محاسبه مساحت این دایره فرضی است. به همین دلیل از توان دوم r در فرمول آن استفاده میشود.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام،سوال دیگهای داشتم
در توضیحات نوشته بود که اینرسی،مقاومتی است که اجسام در هنگام شروع به حرکت دایرهای یا توقف از حرکت دایرهای از خود به نمایش میگذارند. اجسام ممکن است یا حرکت انتقالی یا دورانی ویا ترکیب این دو حرکت را داشته باشند، آیا فقط در حالت دورانی ما ممان اینرسی داریم؟ در حرکت انتقالی ممان اینرسی نداریم؟؟
ممنون
با سلام،
ممان اینرسی تنها در حرکت چرخشی به دور محور تعریف میشود. در حرکت انتقالی یا جرکت روی خط راست از مفهوم اینرسی استفاده میکنیم.
با تشکر از همراهی شما با مجله فرادرس
خیلی کامل و مفید بود
واقعا ممنون