مشتق توابع برداری — به زبان ساده (+ دانلود فیلم آموزش رایگان)
در آموزشهای پیشین مجله فرادرس با توابع برداری و انتگرال آنها آشنا شدیم. در برخی موارد، مثلاً محاسبه مقدار حداکثر یا حداقل تندی یک ذره، لازم است از مشتق توابع برداری استفاده کنیم. در این آموزش، درباره مشتق توابع برداری بحث خواهیم کرد.
تعریف تابع برداری
تابع برداری یکمتغیره در فضای دکارتی سهبعدی به صورت زیر نشان داده میشود:
$$ \large { \mathbf { r } \left ( t \right ) = \left \langle { f \left ( t \right ) , g \left ( t \right ) , h \left ( t \right ) } \right \rangle , } $$ یا $$ \large { { \mathbf { r } \left ( t \right ) = f \left ( t \right ) \mathbf { i } + g \left ( t \right ) \mathbf { j } + h \left ( t \right ) \mathbf { k } } } $$
که در آن $$f(t)$$، $$g(t)$$ و $$h(t)$$ توابع مؤلفهای هستند.
به طور مشابه، در فضای دکارتی دو بعدی، تابع برداری به شکل زیر است:
$$ \large { \mathbf { r } \left ( t \right ) = \left \langle { f \left ( t \right ) , g \left ( t \right ) } \right \rangle . } $$ یا $$ \large { { \mathbf { r } \left ( t \right ) = f \left ( t \right ) \mathbf { i } + g \left ( t \right ) \mathbf { j } } } $$
حد و پیوستگی توابع برداری
فرض کنید که $$\mathbf{r}\left( t \right) = \left\langle {f\left( t \right),g\left( t \right),h\left( t \right)} \right\rangle$$ است. هنگامی که $$t$$ به سمت $$a$$ میل میکند، حد $$\mathbf{r}\left( t \right)$$ برابر است با:
$$ \large { \mathop { \lim } \limits _ { t \to a } \mathbf { r } \left ( t \right ) } = { \mathop { \lim } \limits _ { t \to a } \left \langle { f \left ( t \right ) , g \left ( t \right ) , h \left ( t \right ) } \right \rangle } = { \left \langle { \mathop { \lim } \limits _ { t \to a } f \left ( t \right ) , \mathop { \lim } \limits _ { t \to a } g \left ( t \right ) , \mathop { \lim } \limits _ { t \to a } h \left ( t \right ) } \right \rangle , } $$
البته به شرطی که حد توابع مؤلفهای موجود باشد.
تابع برداری $$\mathbf{r}\left( t \right)$$ در $$t=a$$ پیوسته است، هرگاه
$$ \large { \mathop { \lim } \limits _ { t \to a } \mathbf { r } \left ( t \right ) = \mathbf { r } \left ( a \right ) . } $$
مشتق توابع برداری
مشتق تابع برداری $$\mathbf{r}\left( t \right)$$ به صورت زیر تعریف میشود:
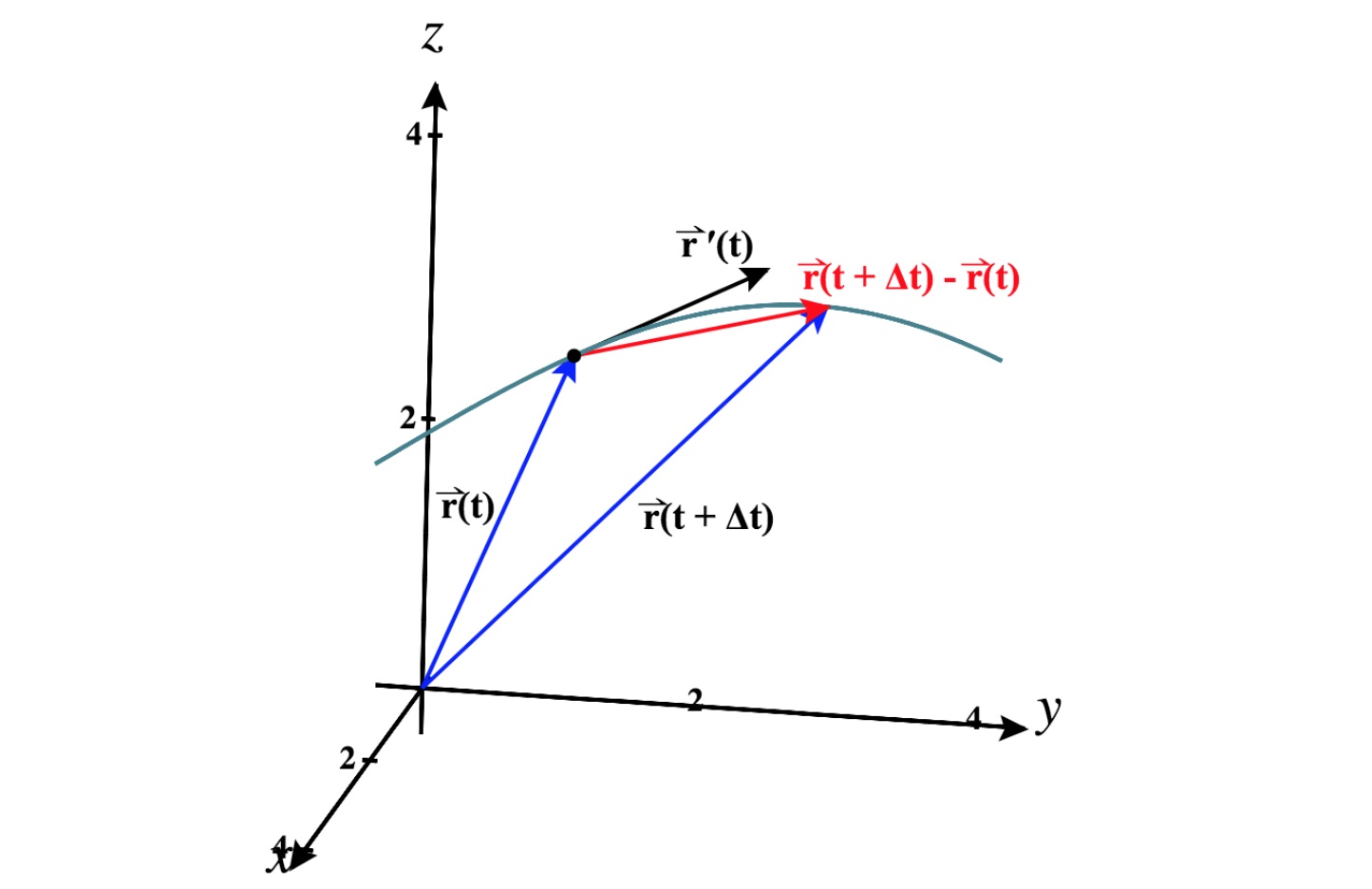
$$ \large { \frac { { d \mathbf { r } } } { { d t } } = \mathbf { r } ^ \prime \left ( t \right ) } = { \mathop { \lim } \limits _ { \Delta t \to 0 } \frac { { \mathbf { r } \left ( { t + \Delta t } \right ) – \mathbf { r } \left ( t \right ) } } { { \Delta t } } } $$
برای هر مقدار از $$t$$ که به ازای آن حد موجود باشد، این رابطه برقرار است. بردار $$\mathbf{r}^\prime\left( t \right)$$ بردار مماس بر منحنی تعریف شده توسط $$\mathbf{r}$$ نامیده میشود.
اگر $$\mathbf{r}\left( t \right) = \left\langle {f\left( t \right),g\left( t \right),h\left( t \right)} \right\rangle$$ باشد و $$f$$، $$g$$ و $$h$$ توابعی مشتقپذیر باشند، آنگاه:
$$ \large { \mathbf { r } ^ \prime \left ( t \right ) = \left \langle { f ^ \prime \left ( t \right ) , g ^ \prime \left ( t \right ) , h ^ \prime \left ( t \right ) } \right \rangle . } $$
بنابراین، برای مشتق گرفتن از توابع برداری کافی است از توابع مؤلفهای آنها مشتق بگیریم.
تفسیر فیزیکی
اگر $$\mathbf{r}\left( t \right)$$ مکان یک ذره را نشان دهد، آنگاه مشتق آن برابر با سرعت ذره خواهد بود:
$$ \large { \mathbf { v } \left ( t \right ) = \frac { { d \mathbf { r } } } { { d t } } = \mathbf { r } ^ \prime \left ( t \right ) . } $$
تندی ذره نیز برابر با اندازه بردار سرعت است:
$$ \large { \left\| { \mathbf { v } \left ( t \right ) } \right\| \text { = } } \kern0pt { \sqrt { { { \left ( { f ^ \prime \left ( t \right ) } \right ) } ^ 2 } + { { \left ( { g ^ \prime \left ( t \right ) } \right ) } ^ 2 } + { { \left ( { h ^ \prime \left ( t \right ) } \right ) } ^ 2 } . } } $$
به روشی مشابه، با مشتق گرفتن از سرعت، شتاب به دست میآید:
$$ \large { \mathbf { a } \left ( t \right ) = \frac { { d \mathbf { v } } } { { d t } } = \mathbf { v } ^ \prime \left ( t \right ) = \mathbf { r } ^ { \prime \prime } \left ( t \right ) . } $$
مثالها
در این بخش، چند مثال را بررسی میکنیم.
مثال ۱
ذرهای در امتداد منحنی زیر حرکت میکند. تندی این ذره را در $$t=1$$ به دست آورید.
$$ \large { \mathbf { r } \left ( t \right ) = \left ( { { t ^2 } – 1 } \right ) \mathbf { i } } + { \left ( { 2 { t ^ 3 } + 3 } \right ) \mathbf { j } + \left ( { 3 t – 4 } \right ) \mathbf { k } . } $$
حل: از تابع برداری $$\mathbf{r}\left( t \right)$$ مشتق میگیریم تا سرعت به دست آید:
$$ \large { { \mathbf { r } ^ \prime \left ( t \right ) = \mathbf { v } \left ( t \right ) } = { 2 t \mathbf { i } + 6 { t ^ 2 } \mathbf { j } + 3 \mathbf { k } . } } $$
اکنون میتوانیم تندی ذره را در $$t=1$$ محاسبه کنیم:
$$ \large { \left \| { \mathbf { v } \left ( t \right ) } \right \| } = { \sqrt { { 2 ^ 2 } + { 6 ^ 2 } + { 3 ^ 2 } } } = { \sqrt { 4 9 } } = { 7 . } $$
مثال ۲
مشتق تابع برداری $$\mathbf{r}\left( t \right) = \left\langle {\sin 2t,{e^{{t^2}}}} \right\rangle$$ را محاسبه کنید.
حل: از هر یک از مؤلفههای تابع برداری مشتق میگیریم و خواهیم داشت:
$$ \large { \left ( { \sin 2 t } \right ) ^ \prime = \cos 2 t \cdot \left ( { 2 t } \right ) ^ \prime } = { 2 \cos 2 t ; } $$
$$ \large \left ( { { e ^ { { t ^ 2 } } } } \right ) ^ \prime = { e ^ { { t ^ 2 } } } \cdot \left ( { { t ^ 2 } } \right ) ^ \prime = 2 t { e ^ { { t ^ 2 } } }. $$
بنابراین، مشتق این تابع برداری برابر است با:
$$ \large \mathbf { r } ^ \prime \left ( t \right ) = \left \langle { 2 \cos 2 t , 2 t { e ^ { { t ^ 2 } } } } \right \rangle . $$
مثال ۳
مشتق تابع برداری $$\mathbf{r}\left( t \right) = \left\langle {\ln t,3t + 1,{t^2}} \right\rangle$$ را در $$t=1$$ به دست آورید.
حل: ابتدا از هر یک از مؤلفههای این تابع مشتق میگیریم:
$$ \large \mathbf { r } ^ \prime \left ( t \right ) = \left \langle { \frac { 1 } { t } , 3 , 2 t } \right \rangle . $$
سپس، مقدار پارامتری $$t=1$$ را جایگذاری میکنیم:
$$ \large { \mathbf { r } ^ \prime \left ( 1 \right ) = \left \langle { 1 , 3 , 2 } \right \rangle } = { \mathbf { i } + 3 \mathbf { j } + 2 \mathbf { k } . } $$
مثال ۴
مشتق تابع برداری $$\mathbf{r}\left( t \right) = \left\langle {\sin \left( {{t^2}} \right),4{t^2} – t} \right\rangle$$ را محاسبه کنید.
حل: ابتدا از هریک از مؤلفههای تابع مشتق میگیریم:
$$ \large { \left ( { \sin \left ( { { t ^ 2 } } \right ) } \right ) ^ \prime = \cos \left ( { { t ^ 2 } } \right ) \cdot \left ( { { t ^ 2 } } \right ) ^ \prime } = { 2 t \cos \left ( { { t ^ 2 } } \right ) ; } $$
$$ \large \left ( { 4 { t ^ 2 } – t } \right ) ^ \prime = 8 t – 1 . $$
بنابراین، مشتق این تابع برداری، به صورت زیر به دست میآید:
$$ \large \mathbf { r } ^ \prime \left ( t \right ) = \left \langle { 2 t \cos \left ( { { t ^ 2 } } \right ) , 8 t – 1 } \right \rangle . $$
مثال ۵
مشتق تابع برداری $$\mathbf{r}\left( t \right) = \left\langle {\sin 2t,\cos t,2\sec t} \right\rangle$$ را در $$t = \large{\frac{\pi }{6}}\normalsize$$ به دست آورید.
حل: از هریک از مؤلفههای تابع مشتق میگیریم:
$$ \large \left ( { \sin 2 t } \right ) ^ \prime = 2 \cos 2 t ; $$
$$ \large \left ( { \cos t } \right ) ^ \prime = – \sin t ; $$
$$ \large { \left ( { 2 \sec t } \right ) ^ \prime = \left ( { \frac { 2 } { { \cos t } } } \right ) ^ \prime } = { – \frac { 2 } { { { { \cos } ^ 2 } t } } \cdot \left ( { – \sin t } \right ) } = { \frac { { 2 \sin t } } { { { { \cos } ^ 2 } t } } . } $$
بنابراین، مشتق تابع برداری برابر است با:
$$ \large \mathbf { r } ^ \prime \left ( t \right ) = \left \langle { 2 \cos 2 t , – \sin t , \frac { { 2 \sin t } } { { { { \cos } ^ 2 } t } } } \right \rangle . $$
مقدار این مشتق در $$t = \large{\frac{\pi }{6}}\normalsize$$ به صورت زیر خواهد بود:
$$ \large \begin {align*}
\mathbf { r } ^ \prime \left ( { \frac { \pi } { 6 } } \right ) & = \kern0pt { \left \langle { 2 \cos \frac { \pi } { 3 } , – \sin \frac { \pi } { 6 } , \frac { { 2 \sin \frac { \pi } { 6 } } } { { { { \cos } ^ 2 } \frac { \pi } { 6 } } } } \right \rangle } = { \left \langle { 2 \cdot \frac { 1 } { 2 } , – \frac { 1 } { 2 } , \frac { { 2 \cdot \frac { 1 } { 2 } } }{ { { { \left ( { \frac { { \sqrt 3 } }{ 2 } } \right ) } ^ 2 } } } } \right \rangle } \\ & = { \left \langle { 1 , – \frac { 1 } { 2 } , \frac { 1 } { { \frac { 3} { 4 } } } } \right \rangle } = { \left \langle { 1 , – \frac { 1 } { 2 } , \frac { 4 } { 3 } } \right \rangle . }
\end {align*} $$
مثال ۶
دو خط راست را در نظر بگیرید که با توابع برداری $${\mathbf{r}_1}\left( t \right) = \left\langle {t,t – 7} \right\rangle$$ و $${\mathbf{r}_2}\left( t \right) = \left\langle {u – 1,2 – u} \right\rangle$$ نشان داده میشوند. زاویه $$\alpha$$ بین این خطوط را بیابید.
حل: برای اینکه راستای این خطوط را تعیین کنیم، بردارهای مماس آنها را به دست میآوریم:
$$ \large { { \mathbf { r } _ 1 ^ \prime } \left ( t \right ) = \left \langle { t ^ \prime , \left ( { t – 7 } \right ) ^ \prime } \right \rangle } = { \left \langle { 1 , 1 } \right \rangle ; } $$
$$ \large { { \mathbf { r } _ 2 } \left ( u \right ) = \left \langle { \left ( { u – 1 } \right ) ^ \prime , \left ( { 2 – u } \right ) ^ \prime } \right \rangle } = { \left \langle { 1 , – 1 } \right \rangle . } $$
زاویه $$\alpha$$ بین خطوط برابر با زاویه بین بردارهای مماس متناظر است. از این رو، با استفاده از ضرب اسکالر خواهیم داشت:
$$ \large { \cos \alpha = \frac { { { x _ 1 } { x _ 2 } + { y _ 1 }{ y _ 2 } } } { { \sqrt { { x _ 1 } + { y _ 1 } } \sqrt { { x _ 2 } + { y _ 2 } } } } } = { \frac { { 1 \cdot 1 + 1 \cdot \left ( { – 1} \right ) } } { { \sqrt { { 1^ 2 } + { 1 ^ 2 } } \sqrt { { 1 ^ 2 } + { { \left ( { – 1 } \right ) } ^ 2 } } } } } = { \frac { 0 } { { \sqrt 2 \sqrt 2 } } } = { 0 . } $$
بنابراین، $$\alpha = \large{\frac{\pi }{2}}\normalsize$$ است و این بدین معنی است که دو خط بر هم عمودند.
مثال ۷
ذرهای در امتداد منحنی زیر حرکت میکند. تندی این ذره را در $$t=1$$ به دست آورید.
$$ \large \mathbf { r } \left ( t \right ) = \left \langle { \frac { { 2 t } } { { 1 + { t ^ 2 } } } , \frac { { 1 – { t ^ 2 } } } { { 1 + { t ^ 2 } } }} \right \rangle . $$
حل: ابتدا باید بردار سرعت را به دست آوریم. به همین منظور، از مؤلفههای بردار مکان $$\mathbf{r}\left( t \right)$$ مشتق میگیریم:
$$ \large { \left ( { \frac { { 2 t } } { { 1 + { t ^ 2 } } } } \right ) ^ \prime = \frac { { 2 \cdot \left ( { 1 + { t ^ 2 } } \right ) – 2 t \cdot 2 t } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } } = { \frac { { 2 + 2 { t ^ 2 } – 4 { t ^ 2 } } } { { { { \left( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } } = { \frac { { 2 \left ( { 1 – { t ^ 2 } } \right ) } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } ; } $$
$$ \large \begin {align*}
\require {cancel} \left ( { \frac { { 1 – { t ^ 2 } } } { { 1 + { t ^ 2 } } } } \right ) ^ \prime & = \kern0pt { \frac { { \left ( { – 2 t } \right ) \cdot \left ( { 1 + { t ^ 2 } } \right ) – \left ( { 1 – { t ^ 2 } } \right ) \cdot 2 t } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } } \\ & = { \frac { { – 2 t – \cancel { 2 { t ^ 3 } } – 2 t + \cancel { 2 { t ^ 3 } } } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } } = { \frac { { – 4 t } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } . }
\end {align*} $$
در نتیجه، بردار سرعت به صورت زیر خواهد بود:
$$ \large { \mathbf { v } \left ( t \right ) \text { = }} \kern0pt { \left \langle { \frac { { 2 \left ( { 1 – { t ^ 2 } } \right ) } }{ { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } , \frac { { – 4 t } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } } \right \rangle } $$
یا
$$ \large \mathbf { v } \left ( t \right ) = \frac { { 2 \left ( { 1 – { t ^ 2 } } \right ) } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } } \mathbf { i } – \frac { { 4 t } } { { { { \left ( { 1 + { t ^ 2 } } \right ) } ^ 2 } } }\mathbf { j } . $$
سرعت ذره در $$t=1$$ برابر است با:
$$ \large { \mathbf { v } \left ( 1 \right ) = \frac { { 2 \left ( { 1 – { 1 ^ 2 } } \right ) } } { { { { \left ( { 1 + { 1 ^ 2 } } \right ) } ^ 2 } } } \mathbf { i } – \frac { { 4 \cdot 1 } } { { { { \left ( { 1 + { 1 ^ 2 } } \right ) } ^ 2 } } } \mathbf { j } } = { 0 \cdot \mathbf { i } – 1 \cdot \mathbf { j } } = { – \mathbf { j } . } $$
تندی ذره برابر با اندازه بردار سرعت است. در نتیجه:
$$ \large \left | { \mathbf { v } \left ( 1 \right ) } \right | = \sqrt { { 0 ^ 2 } + { { \left ( { – 1 } \right ) } ^ 2 } } = 1 . $$
مثال ۸
ذرهای روی منحنی $$\mathbf{r}\left( t \right) = \left\langle {\arctan t,\sqrt {t + 1} } \right\rangle$$ حرکت میکند. تندی این ذره را در $$t=3$$ به دست آورید.
حل: برای یافتن بردار سرعت، از $$\mathbf{r}\left( t \right)$$ مشتق میگیریم:
$$ \large { \mathbf { v } \left ( t \right ) = \mathbf { r } ^ \prime \left ( t \right ) = \left \langle { \left ( { \arctan t } \right ) ^ \prime , \left ( { \sqrt { t + 1 } } \right ) ^ \prime } \right \rangle } = { \left \langle { \frac { 1 } { {1 + { t ^ 2 } } } , \frac { 1 } { { 2 \sqrt { t + 1 } } } } \right \rangle . } $$
در $$t=3$$، این سرعت برابر است با:
$$ \large { \mathbf { v } \left ( 3 \right ) = \left \langle { \frac { 1 } { { 1 + { 3 ^ 2 } } } , \frac { 1 } { { 2 \sqrt { 3 + 1 } } } } \right \rangle } = { \left \langle { \frac { 1 } { { 1 0 } } , \frac { 1 } { 4 } } \right \rangle . } $$
و در نهایت، تندی به صورت زیر به دست میآید:
$$ \large \begin {align*} \left | { \mathbf { v } \left ( 3 \right ) } \right | & = \sqrt { { { \left ( { \frac { 1 } { { 1 0 } } } \right ) } ^ 2 } + { { \left ( { \frac { 1 } { 4 } } \right ) } ^ 2 } } ={ \sqrt {\frac{1}{{100}} + \frac{1}{{16}}} } \\ & = { \sqrt { \frac { 4 } { { 4 0 0 } } + \frac { { 2 5 } } { { 4 0 0 } } } } = { \frac { { \sqrt { 2 9 } } } { { 2 0 } } . } \end {align*} $$
مثال ۹
دو منحنی صفحهای را در نظر بگیرید که با توابع برداری $${\mathbf{r}_1}\left( t \right) = \left\langle {t,2t – 4} \right\rangle$$ و $${\mathbf{r}_2}\left( u \right) = \left\langle {2u,{u^2}} \right\rangle$$ تعریف میشوند. زاویه $$\alpha$$ بین این منحنیها را در نقطه تلاقیشان بیابید.
حل: ابتدا با حل دستگاه معادلات زیر، مختصات نقطه تلاقی منحنیها را تعیین میکنیم:
$$ \large { \left \{ \begin {array} {l}
t = 2 u \\
2 t – 4 = { u ^ 2 }
\end {array} \right . , } \; \; \Rightarrow { \left \{ \begin {array} {l}
t = 2 u \\
4 u – 4 = { u ^ 2 }
\end {array} \right . , } \; \; \Rightarrow { \left \{ \begin {array} {l}
{ u ^ 2 } – 4 u + 4 = 0 \\
t = 2 u
\end {array} \right . , } \; \; \\ \large \Rightarrow { \left \{ \begin {array} {l}
{ \left ( { u – 2 } \right ) ^ 2 } = 0 \\
t = 2 u
\end {array} \right . , } \; \; \Rightarrow { \left \{ \begin {array} {l}
u = 2 \\
t = 4
\end {array} \right . . } $$
حال از این دو تابع مشتق میگیریم و بردارهای مماس در نقطه تلاقی را به دست میآوریم:
$$ \large { { \mathbf { r } _ 1 ^ \prime } \left ( t \right ) = \left \langle { t ^ \prime , \left ( { 2 t – 4 } \right ) ^ \prime } \right \rangle } = { \left \langle { 1 , 2 } \right \rangle ; } $$
$$ \large { { \mathbf { r } _ 2 ^ \prime } \left ( u \right ) = \left \langle { \left ( { 2 u } \right ) ^ \prime , \left ( { { u ^ 2 } } \right ) ^ \prime } \right \rangle } = { \left \langle { 2 , 2 u } \right \rangle . } $$
در نقطه تلاقی که $$t=4$$ و $$u=2$$ است، بردارهای مماس برابرند با:
$$ \large { { \mathbf { r } _ 1 ^ \prime } \left ( t \right ) = \left \langle { 1 , 2 } \right \rangle , \; \; } \kern0pt { { \mathbf { r } _ 2 ^ \prime } \left ( u \right ) = \left \langle { 2 , 4 } \right \rangle . } $$
زاویه $$\alpha$$ بین منحنیها برابر با زاویه بین خطوط مماس متناظر است. در نتیجه، با استفاده از ضرب اسکالر خواهیم داشت:
$$ \large \begin {align*} \cos \alpha & = \frac { { { x _ 1 } { x _ 2 } + { y _ 1 } { y _ 2 } } } { { \sqrt { { x _ 1 ^2 } + { y _ 1 ^ 2 } } \sqrt { { x _ 2 ^ 2 } + { y _ 2 ^2 } } } } = { \frac { { 1 \cdot 2 + 2 \cdot 4 } } { { \sqrt { { 1 ^ 2 } + { 2 ^ 2 } } \sqrt { { 2 ^ 2 } + { 4 ^ 2 } } } } } \\ &= { \frac { { 1 0 } } { { \sqrt 5 \sqrt { 2 0 } } } } = { \frac { { 1 0 } } { { \sqrt { 1 0 0 } } } = 1 . } \end {align*} $$
بنابراین، $$\alpha=0$$ است.
مثال ۱۰
ذرهای در امتداد منحنی $$\mathbf{r}\left( t \right) = \left\langle {{t^2},{t^2} – 4t,t} \right\rangle$$ در حرکت است. مینیمم تندی این ذره را به دست آورید.
حل: ابتدا بردار سرعت را به دست میآوریم:
$$ \large { \mathbf { v } \left ( t \right ) = \mathbf { r } ^ \prime \left ( t \right ) } = { \left \langle { \left ( { { t ^ 2 } } \right ) ^ \prime , \left ( { { t ^ 2 } – 4 t } \right ) ^ \prime , t ^ \prime } \right \rangle } = { \left \langle { 2 t ,2 t – 4 , 1 } \right \rangle . } $$
بنابراین، تندی ذره برابر است با:
$$ \large \begin {align*}
\left | { \mathbf { v } \left ( t \right ) } \right | & = \sqrt { { { \left ( { 2 t } \right ) } ^ 2 } + { { \left ( { 2 t – 4 } \right ) } ^ 2 } + { 1 ^ 2 } } = { \sqrt { 4 { t ^ 2 } + 4 { t ^ 2 } – 1 6 t + 1 6 + 1} } \\ &= { \sqrt { 8 { t ^ 2 } – 1 6 t + 1 7 } . }
\end {align*} $$
اکنون به ازای مقادیر اکسترمم تندی را محاسبه میکنیم. برای این کار، ابتدا تندی را با $$F\left( t \right)$$ نمایش میدهیم و نسبت به زمان $$t$$ از آن مشتق میگیریم:
$$ \large \begin {align*}
F ^ \prime \left ( t \right ) & = \left ( { \sqrt { 8 { t ^ 2 } – 1 6 t + 1 7 } } \right ) ^ \prime = { \frac { { \left ( { 8 { t ^ 2 } – 1 6 t + 1 7 } \right ) ^ \prime } } { { 2 \sqrt { 8 { t ^ 2 } – 1 6 t + 1 7 } } } } \\ & = { \frac { { 1 6 t – 1 6} } { { 2 \sqrt { 8 { t ^ 2 } – 1 6 t + 1 7 } } } } = { \frac { { 8 t – 8 } }{ { 2 \sqrt { 8 { t ^ 2} – 1 6 t + 1 7 } } } . }
\end {align*} $$
واضح است که به ازای $$t=1$$، $$F^\prime\left( t \right) = 0$$ خواهد بود. این مقدار یک نقطه مینیمم را نشان میدهد، چون علامت $$F^\prime\left( t \right) = 0$$ هنگام گذر از این نقطه از منفی به مثبت تغییر میکند.
حال میتوانیم مقدار مینیمم تندی را محاسبه کنیم:
$$ \large { { \left | \mathbf { v } \right | _ { \min } } = \left | { \mathbf { v } \left ( 1 \right ) } \right | } = { \sqrt { 8 \cdot { 1 ^ 2 } – 1 6 \cdot 1 + 1 7 } } = { \sqrt 9 } = { 3 . } $$
مثال ۱۱
مکان ذرهای توسط بردار $$\mathbf{r}\left( t \right) = \left\langle {\sin t,\cos 2t} \right\rangle$$ نشان داده میشود. ماکزیمم تندی این ذره را به دست آورید.
حل: بردار سرعت این ذره به صورت زیر خواهد بود:
$$ \large { \mathbf { v } \left ( t \right ) = \mathbf { r } ^ \prime \left ( t \right ) } = { \left\langle { \left ( { \sin t } \right ) ^ \prime , \left ( { \cos 2 t } \right ) ^ \prime } \right \rangle } = { \left \langle { \cos t , – 2 \sin 2 t } \right \rangle . } $$
بنابراین، تندی ذره برابر است با:
$$ \large \left | { \mathbf { v } \left ( t \right ) } \right | = \sqrt { { { \cos } ^ 2 } t + 4 { { \sin } ^ 2 } 2 t } . $$
از تساوی $$\sin 2 t = 2 \sin t \cos t $$ استفاده میکنیم و خواهیم داشت:
$$ \large \begin {align*}\left | { \mathbf { v } \left ( t \right ) } \right | & = \sqrt { { { \cos } ^ 2 } t + 4 { { \sin } ^ 2 } 2 t } = \sqrt { { { \cos } ^ 2 } t + 16 { { \sin } ^ 2 } t\cos^2t }\\
& =\sqrt { { { \cos } ^ 2 } t (1+ 16 (1- \cos^2t ))}= \sqrt { { { \cos } ^ 2 } t (17 - 16 \cos^2t )}. \end {align*} $$
اکنون برای راحتی تساوی $$\cos t ^ 2 = Z $$ را در نظر میگیریم و داریم:
$$ \large \left | { \mathbf { v }\left ( t \right ) } \right | = \sqrt {Z(17-16Z) } . $$
حال مقادیر اکسترمم این تابع را به دست میآوریم. به همین منظور، عبارت زیر رادیکال را با $$F\left( t \right)$$ نشان میدهیم و مقادیر اکسترمم آن را پیدا میکنیم. در نتیجه، خواهیم داشت:
$$ \large F = 17 Z - 16Z^2$$
مشتق را برابر با صفر قرار میدهیم و نقاط بحرانی را تعیین میکنیم:
$$\large F' = 17-32 Z = 0 \Rightarrow Z = \frac {17}{32}$$
بنابراین، داریم:
$$\large \cos t = \pm \sqrt {\frac {17}{32}} $$
در نتیجه، تابع $$F(t)$$ دارای نقاط بحرانی زیر است:
$$\large t = n \pi \pm \arccos \sqrt {\frac {17}{32}}, \;\; n \in Z $$
برای هر یک از این نقاط، مقدار تندی ذره را محاسبه میکنیم:
$$ \large \left | { \mathbf { v }\left ( t \right ) } \right | _{\max}= \sqrt {Z(17-16Z) } = \sqrt {\frac {17}{32}(17-16(\frac{17}{32}) } =\frac {17}{8}\; \text{m/s}. $$
بنابراین، ماکزیمم تندی این ذره برابر است با $$\frac {17}{8}\; \text{m/s}$$.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- خمیدگی توابع برداری — به زبان ساده
- کرل (Curl) در ریاضی — به زبان ساده
- گرادیان (Gradient) در ریاضیات — به زبان ساده










