مساحت بیضی با انتگرال — اثبات فرمول به زبان ساده

انتگرال‌گیری، یکی از روش‌های محاسبه اندازه سطح درون شکل‌های هندسی است. مساحت بیضی‌ها را نیز می‌توان با استفاده از قواعد انتگرال‌گیری محاسبه کرد. در این روش، معادله بیضی نوشته می‌شود. سپس، فرمول مساحت بیضی با انتگرال‌گیری از این معادله در یک بازه مشخص به دست می‌آید. خروجی نهایی این انتگرال، همان فرمول مساحت بیضی با شعاع است. در این مقاله، به معرفی نحوه محاسبه مساحت بیضی با انتگرال به همراه حل مثال می‌پردازیم. علاوه بر این، فرمول مساحت بیضی با قطر را نیز اثبات می‌کنیم.

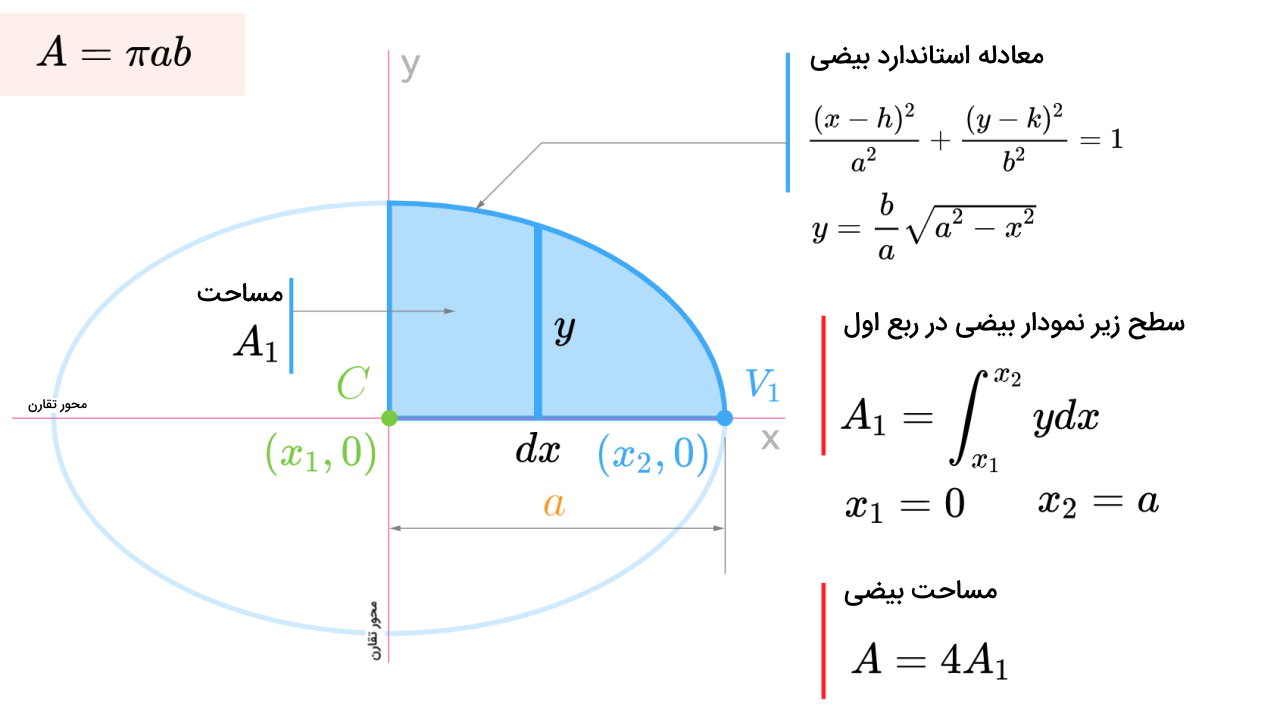
بیضی و مساحت آن

بیضی، یک منحنی بسته است که در اطراف دو نقطه کانونی تشکیل می‌شود.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

مجموع فاصله‌های نقاط بیضی تا دو کانون آن، همواره عددی ثابت است.

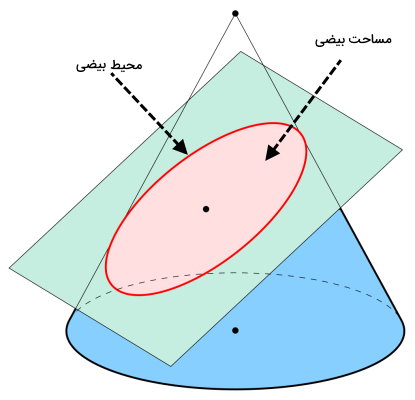
اگر صفحه‌ای را به صورت مایل با یک مخروط برخورد دهیم، در محل اشتراک این دو شکل هندسی، بیضی تشکیل می‌شود. به عبارت دیگر، بیضی، سطح مشترک حاصل از برخورد صفحه مورب و مخروط است. سطح قرمز رنگ در تصویر زیر، یک بیضی را نمایش می‌دهد. به اندازه این سطح، مساحت بیضی می‌گویند.

برای محاسبه مساحت بیضی، روش‌های مختلفی وجود دارد. در ساده‌ترین حالت می‌توان مساحت بیضی را از ضرب شعاع بزرگ در شعاع کوچک در عدد پی به دست آورد.

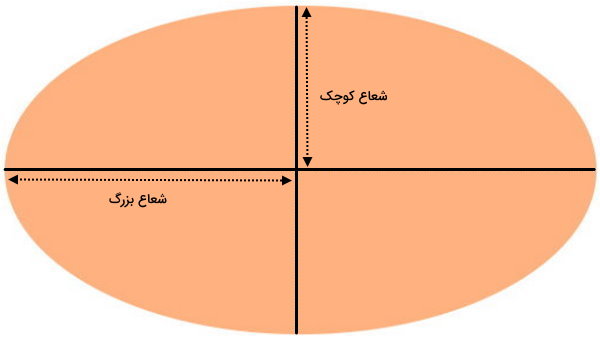
فرمول مساحت بیضی با شعاع عبارت است از:

شعاع کوچک × شعاع بزرگ × ۳/۱۴ = مساحت بیضی

یکی دیگر از روش‌های محاسبه مساحت بیضی، استفاده از مفهوم انتگرال است. در ادامه به توضیح این روش و اثبات فرمول مساحت بیضی می‌پردازیم.

مساحت بیضی با انتگرال

به معادله سطح زیر یک نمودار، انتگرال تابع آن نمودار می‌گویند. انتگرال‌گیری، یکی از فرآیندهای اصلی در حوزه حسابان است که معمولا به منظور تعیین سطح زیر نمودارها مورد استفاده قرار می‌گیرد.

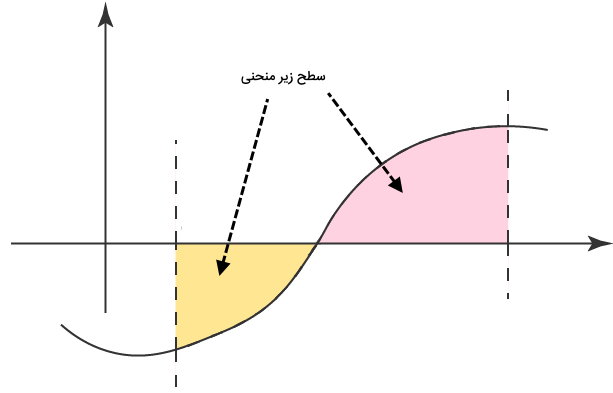
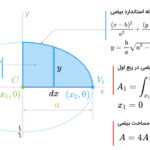
انتگرال‌گیری، یکی از روش‌های محاسبه و اثبات فرمول مساحت بیضی است. بیضی زیر را در نظر بگیرید. مرکز این بیضی، بر روی مبدا مختصات قرار دارد.

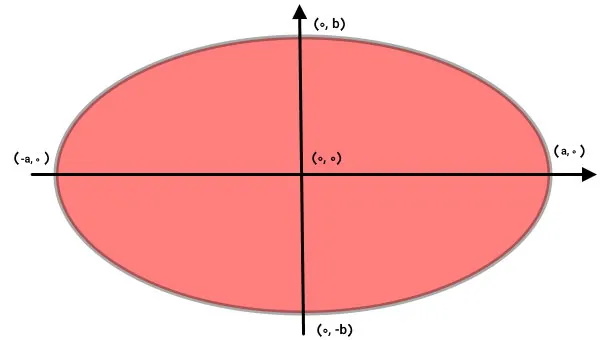
محیط بیضی را می‌توان مانند یک منحنی در محورهای مختصات در نظر گرفت. معادله این منحنی به صورت زیر نوشته می‌شود:

$$\frac { x ^ { ۲ } } { a ^ { ۲ } } + \frac { y ^ { ۲ } } { b ^ { ۲ } } = ۱$$

a، شعاع بزرگ بیضی و b، شعاع کوچک بیضی را نمایش می‌دهد. x و y، مختصات طولی و عرضی نقاط روی بیضی هستند. اگر مبدا بیضی بر روی نقطه دیگری مانند (h,k) قرار داشته باشد، معادله بیضی به شکل زیر در می‌آید:

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

$$\frac { (x - h ) ^ { ۲ } } { a ^ { ۲ } } + \frac { ( y - k ) ^ { ۲ } } { b ^ { ۲ } } = ۱$$

این معادلات را به خاطر داشته باشید. بیضی، یکی از شکل‌های هندسی متقارن محسوب می‌شود. شکل بیضی، در راستای محور اصلی و فرعی خود (قطرهای بزرگ و کوچک)، دارای تقارن محوری است. قطرهای بزرگ و کوچک، این شکل را به چهار قسمت مساوی تقسیم می‌کنند. وجود تقارن محوری، نکته مهمی در نوشتن فرمول مساحت بیضی با انتگرال است.

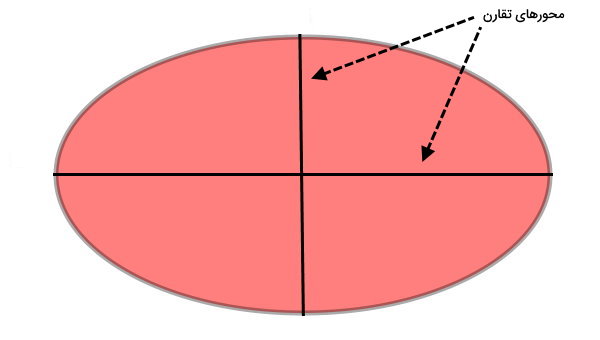
با استفاده از معادله بیضی، رابطه منحنی آن را بر حسب مقادیر y می‌نویسیم:

$$y = \pm \frac { b } { a } \sqrt { a ^ { ۲ } - x ^ { ۲ } }$$

اگر از معادله بالا در بازه ۰ تا a (بازه تغییرات مثبت محور افقی x) انتگرال بگیریم، سطح زیر منحنی بیضی در ربع اول به دست می‌آید.

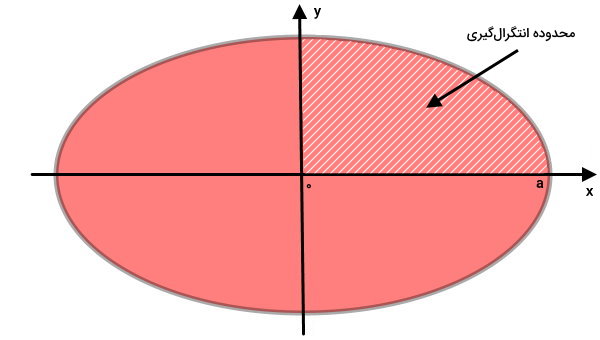
در واقع، مساحت بیضی در ربع اول، برابر است با:

$$A _ { ۱ } = \int _ { ۰ } ^ { a } \frac { b } { a } \sqrt { a ^ { ۲ } - x ^ { ۲ } } d x$$

اندازه هر قسمت بیضی در هر ربع، برابر با اندازه قسمت‌های دیگر است. بنابراین، رابطه بالا، فرمول محاسبه یک‌چهارم مساحت بیضی کامل را نمایش می‌دهد. به منظور نوشتن فرمول مساحت کامل بیضی، باید این رابطه را در عدد ۴ ضرب کنیم. از این‌رو، فرمول مساحت بیضی با انتگرال به صورت زیر نوشته می‌شود:

$$A = ۴ \space \int _ { ۰ } ^ { a } \frac { b } { a } \sqrt { a ^ { ۲ } - x ^ { ۲ } } d x$$

به این ترتیب، می‌توانیم مساحت بیضی را با استفاده از انتگرال بالا به دست بیاوریم.

نکته: معادله منحنی بیضی را می‌توانستیم بر حسب x نیز بنویسیم. در این حالت، باید بازه انتگرال را بر روی محور y در نظر می‌گرفتیم. خروجی عددی انتگرال در هر دو حالت یکسان خواهد بود اما پارامترهای مورد استفاده تغییر می‌کنند.

مثال: تعیین معادله مساحت بیضی با انتگرال

معادله یک بیضی به صورت زیر نوشته می‌شود:

$$۲۵ x ^ { ۲ } + ۴ y ^ { ۲ } \le ۱۰۰$$

اندازه قطرهای بزرگ و کوچک بیضی را به دست بیاورید. شکل تقریبی بیضی را رسم کنید. سپس، فرمول مساحت بیضی با انتگرال را بنویسید.

به منظور تعیین اندازه قطرهای بیضی، ابتدا باید معادله آن را به فرم استاندارد در بیاوریم. شکل استاندارد معادله بیضی عبارت است از:

$$\frac { x ^ { ۲ } } { a ^ { ۲ } } + \frac { y ^ { ۲ } } { b ^ { ۲ } } = ۱$$

بر اساس رابطه بالا، برای اینکه معادله بیضی مورد سوال را به فرم استاندارد در بیاوریم، باید سمت راست معادله را به عدد ۱ تبدیل کنیم. این کار، با تقسیم دو طرف معادله بر عدد ۱۰۰ انجام می‌گیرد:

$$\frac { ۲۵ x ^ { ۲ } + ۴ y ^ { ۲ } } { ۱۰۰ }\le \frac { ۱۰۰ } { ۱۰۰ }$$

$$\frac { ۲۵ x ^ { ۲ } } { ۱۰۰ } + \frac { ۴ y ^ { ۲ } } { ۱۰۰ }\le \frac { ۱۰۰ } { ۱۰۰ }$$

$$\frac { x ^ { ۲ } } { ۴ } + \frac { y ^ { ۲ } } { ۲۵ }\le ۱$$

$$\frac { x ^ { ۲ } } { ۲ ^ { ۲ } } + \frac { y ^ { ۲ } } { ۵ ^ { ۲ } }\le ۱$$

اکنون می‌توانیم اندازه قطرهای بزرگ و کوچک بیضی را به دست بیارویم. در معادله استاندارد بالا، مخرج کسرها، شعاع‌های کوچک و بزرگ را نمایش می‌دهند. شعاع کوچک بیضی برابر با ۲ و شعاع بزرگ آن برابر با ۵ است. بنابراین، قطر کوچک بیضی برابر با ۴ و قطر بزرگ آن برابر با ۱۰ خواهد بود. تصویر زیر را می‌توان به عنوان شکل تقریبی این بیضی در نظر گرفت.

راستای قطر کوچک بر روی محور افقی x و راستای قطر بزرگ بر روی محور عمودی y است. بنابراین، کشیدگی شکل بیضی در راستای عمودی خواهد بود. معادله مساحت بیضی با انتگرال به صورت زیر نوشته می‌شود:

$$A = ۴ \space \int _ { ۰ } ^ { a } \frac { b } { a } \sqrt { a ^ { ۲ } - x ^ { ۲ } } d x$$

• A: مساحت بیضی
• a: شعاع بیضی در راستای محور x
• b: شعاع بیضی در راستای محور y

با توجه به شکل، شعاع بیضی در راستای محور x برابر با ۲ و شعاع بیضی در راستای محور y برابر با ۵ است. بنابراین، رابطه مساحت بیضی مورد سوال با انتگرال، عبارت است از:

$$A = ۴ \space \int _ { ۰ } ^ { ۲ } \frac { ۵ } { ۲ } \sqrt { ۲ ^ { ۲ } - x ^ { ۲ } } d x$$

به دلیل مشخص بودن اندازه شعاع‌های بزرگ و کوچک (۵ و ۲)، می‌توانیم مقدار مساحت را توسط رابطه زیر محاسبه کنیم:

$$A = \pi a b$$

اگر مقدار π را برابر با ۳/۱۴ در نظر بگیریم، خواهیم داشت:

$$A = ۳/۱۴ \times ۵ \times ۲$$

$$A = ۳۱/۴$$

با گرفتن انتگرال نیز به مساحت بالا می‌رسیدم. در واقع، تمام روش‌های محاسبه مساحت بیضی، به فرمول اصلی آن (حاصلضرب شعاع‌ها در عدد پی) ختم می‌شوند. در بخش بعدی، این قضیه را با استفاده از انتگرال اثبات می‌کنیم.

اثبات فرمول مساحت بیضی با قطر به کمک انتگرال

اگر حل مساحت بیضی با انتگرال را ادامه دهیم، به فرمول مساحت بیضی با قطر می‌رسیم. به این منظور، انتگرال زیر را در نظر بگیرید:

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

$$A = ۴ \space \int _ { ۰ } ^ { a } \frac { b } { a } \sqrt { a ^ { ۲ } - x ^ { ۲ } } d x$$

در این انتگرال، مقادیر a و b (قطرهای بیضی)، ثابت‌های عددی هستند. بنابراین می‌توانیم آن‌ها از درون انتگرال خارج کنیم و به پشت انتگرال (در کنار عدد ثابت ۴) انتقال دهیم:

$$A = \frac { ۴b } { a } \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } - x ^ { ۲ } } d x$$

برای حل انتگرال بالا، باید x و dx را به پارامترهای مثلثاتی تبدیل کنیم. بر اساس قواعد تغییر متغیر در انتگرال‌ها، داریم:

$$x = a \sin { \theta }$$

$$d x = a \cos \theta \cdot { d \theta }$$

اکنون به جای x، متغیر جایگزین آن‌ها را درون انتگرال قرار می‌دهیم:

$$A = \frac { ۴b } { a } \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } - ( a \sin { \theta } ) ^ { ۲ } } d x$$

$$A = \frac { ۴b } { a } \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } - a ^ { ۲ } \sin ^ { ۲ } { \theta } } \space \space \space d x$$

جای dx را نیز با متغیر جایگزین عوض می‌کنیم:

$$A = \frac { ۴b } { a } \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } - a ^ { ۲ } \sin ^ { ۲ } { \theta } } \space \space \space a \cos \theta \cdot { d \theta }$$

a را از درون انتگرال بیرون می‌کشیم:

$$A = \frac { ۴b a } { a } \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } - a ^ { ۲ } \sin ^ { ۲ } { \theta } } \space \space \space \cos \theta \cdot { d \theta }$$

به این ترتیب، انتگرال به شکل زیر در می‌آید:

$$A = ۴b \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } - a ^ { ۲ } \sin ^ { ۲ } { \theta } } \space \space \space \cos \theta \cdot { d \theta }$$

از عبارت a^۲ در زیر رادیکال، فاکتور می‌گیریم:

$$A = ۴b \int _ { ۰ } ^ { a } \sqrt { a ^ { ۲ } ( ۱ - \sin ^ { ۲ } { \theta } ) } \space \space \space \cos \theta \cdot { d \theta }$$

a^۲ از زیر رادیکال بیرون می‌آید و به a تبدیل می‌شود:

$$A = ۴b \int _ { ۰ } ^ { a } a \sqrt { ۱ - \sin ^ { ۲ } { \theta } } \space \space \space \cos \theta \cdot { d \theta }$$

a را به بیرون از انتگرال منتق می‌کنیم:

$$A = ۴b a \int _ { ۰ } ^ { a } \sqrt { ۱ - \sin ^ { ۲ } { \theta } } \space \space \space \cos \theta \cdot { d \theta }$$

بر اساس روابط مثلثاتی، عبارت زیر رادیکال را می‌توان به صورت زیر نوشت:

$$۱ - \sin ^ { ۲ } \theta= \cos ^ { ۲ } \theta$$

بنابراین، داریم:

$$A = ۴b a \int _ { ۰ } ^ { a } \sqrt { \cos ^ { ۲ } { \theta } } \space \space \space \cos \theta \cdot { d \theta }$$

$$A = ۴b a \int _ { ۰ } ^ { a } \cos { \theta } \space \cos \theta \cdot { d \theta }$$

$$A = ۴b a \int _ { ۰ } ^ { a } \cos ^ { ۲ } { \theta } \cdot { d \theta }$$

عبارت داخل انتگرال، برابر است با:

$$\cos ^ { ۲ } { \theta } = \frac { ۱ }{ ۲ }[ ۱ + \cos {۲ \theta } ]$$

این عبارت را درون انتگرال قرار می‌دهیم:

$$A = ۴b a \int _ { ۰ } ^ { a } \frac { ۱ }{ ۲ }[ ۱ + \cos {۲ \theta } ] { d \theta }$$

عدد ۲ با عدد ۴ در پشت انتگرال ساده می‌شود:

$$A = ۲b a \int _ { ۰ } ^ { a } [ ۱ + \cos {۲ \theta } ] { d \theta }$$

با گرفتن انتگرال بالا، به عبارت زیر می‌رسیم:

$$A = ۲ b a\left [ \theta + \frac { \sin ۲ \theta } { ۲ } \right ] _ { ۰ } ^ { a }$$

این عبارت را به خاطر بسپارید. پیش از ادامه حل این عبارت، رابطه‌های بین پارامترهای مختلف را معرفی می‌کنیم. این روابط عبارت هستند از:

$$\sin { \theta } = \frac { x } { a }$$

$$\theta = \sin ^ { -۱ } ({ \frac { x } { a } } )$$

$$\sin ^ {۲} { \theta } = ۲ \sin \theta \cos \theta$$

$$\cos { \theta } = \frac { \sqrt { a ^ { ۲ } - x ^ { ۲ } } } { a }$$

این عبارت‌ها را درون رابطه مساحت جایگذاری می‌کنیم:

$$A = ۲ b a \space \left [ \sin ^ { -۱ } ({ \frac { x } { a } } ) + \frac { ۲ \sin \theta \cos \theta } { ۲ } \right ] _ { ۰ } ^ { a }$$

$$A = ۲ b a \space \left [ \sin ^ { -۱ } ({ \frac { x } { a } } ) + \sin \theta \cos \theta \right ] _ { ۰ } ^ { a }$$

$$A = ۲ b a\left [ \sin ^ { -۱ } ({ \frac { x } { a } } ) + \frac { x } { a } \times \frac { \sqrt { a ^ { ۲ } - x ^ { ۲ } } } { a } \right ] _ { ۰ } ^ { a }$$

اکنون، رابطه بالا را در بازه ۰ تا a حل می‌کنیم:

$$A = ۲ b a\left [ \sin ^ { -۱ } ({ \frac { a } { a } } ) + \frac { a } { a } \times \frac { \sqrt { a ^ { ۲ } - a ^ { ۲ } } } { a } \right ] - ۲ b a\left [ \sin ^ { -۱ } ({ \frac { ۰ } { a } } ) + \frac { ۰ } { a } \times \frac { \sqrt { a ^ { ۲ } - ۰ ^ { ۲ } } } { a } \right ]$$

$$A = ۲ b a\left [ \sin ^ { -۱ } ( ۱ ) + \frac {۰} { a } \right ] - ۲ b a\left [ \sin ^ { -۱ } ( ۰ ) \right ]$$

سینوس زاویه ۹۰ درجه یا همان پی‌دوم (π/۲) برابر با ۱ می‌شود. سینوس زاویه ۰ درجه، برابر با ۰ است. بنابراین، به جای معکوس سینوس ۱، پی‌دوم و به جای معکوس سینوس ۰، عدد ۰ را قرار می‌دهیم:

$$A = ۲ b a\left [ \frac { \pi } { ۲ }\right ] - ۲ b a\left [ ۰ \right ]$$

$$A = b a \frac { ۲ \pi } { ۲ }- ۰$$

$$A = b a \pi$$

این رابطه، همان فرمول مساحت بیضی با قطر است.