مدل هولت وینترز (Holt-Winters) در سری زمانی — راهنمای کاربردی

کار با سری‌های زمانی (Time Series) و تحلیل آن‌ها، یکی از مسائل مهم در «علم داده» (Data Science) محسوب می‌شود. از طرفی برای استفاده از الگوهای مختلف سری زمانی مانند MA، AR و ARMA یا ARIMA باید آن‌ها را «هموار» (Smooth) یا «ایستا» (Stationary) کرد. روش‌های مختلفی برای هموارسازی وجود دارد. در این نوشتار به بررسی روش «هموارسازی نمایی» (Exponential Smoothing) پرداخته و یکی از مدل‌های پیش‌بینی سری زمانی به نام مدل هولت وینترز (Holt-Winters) را مورد بررسی قرار می‌‌دهیم.

به منظور آشنایی بیشتر با روش هموارسازی نمایی نوشتار هموار سازی نمایی سری زمانی --- راهنمای کاربردی و برای آگاهی از انواع مدل‌های سری زمانی نیز تحلیل سری زمانی با پایتون — مقدمات و مفاهیم اولیه و تحلیل سری زمانی با پایتون — معرفی انواع مدل ها را مطالعه کنید. همچنین خواندن سری زمانی در علم داده — از صفر تا صد و تحلیل سری زمانی — تعریف و مفاهیم اولیه نیز خالی از لطف نیست.

سری زمانی با مدل هولت وینترز (Holt-Winters)

پیش‌بینی داده‌های سری زمانی و مدل‌سازی برای آن‌ها، با بهره‌گیری از هموارسازی و مدل «هولت وینترز» (Holt-Winters) بسیار جذاب و البته نوآورانه است. ولی متاسفانه عدم آگاهی از نحوه به کارگیری و آشنایی با این مدل در بین بسیاری از تحلیل‌گرهای داده (Data Scientists) کمتر به کار گرفته شده است. همچنین هموارسازی و مدل هولت وینترز برای شناسایی داده‌های «نامتعارف» (Anomaly) نیز می‌تواند به کار آید. همانطور که گفته شد، مدل هولت وینترز روشی برای بررسی داده‌های وابسته به زمان است. پیش‌بینی رفتار داده‌های تصادفی، احتیاج به یک مدل آماری دارد که معمولا پارامترهای این مدل توسط داده‌ها، شناسایی و برآورد می‌شود.

فیلم آموزش تحلیل سری های زمانی با پایتون و آر R در فرادرس

کلیک کنید

مدل هولت وینترز، شامل سه بخش است. بخش اول، میانگین (مقدار ثابت) نامیده می‌شود که رفتار کلی مدل را نشان می‌دهد و مقادیر پیرامون آن نوسان می‌کنند. بخش دوم روند (شیب خط) است که برحسب زمان ثابت است ولی به عنوان مضرب برای متغیر در نظر گرفته می‌شود. بخش سوم نیز که بصورت تناوبی تغییر می‌کند، برای نمایش تغییرات فصلی به کار گرفته می‌شود. پیش‌بینی در روش هولت وینترز به کمک هموارسازی نمایی صورت می‌گیرد، به این ترتیب اثر داده‌های نزدیک به نقطه پیش‌بینی، بیشتر از داده‌هایی است که در گذشته دور از آن واقع شده‌اند.

از آنجایی که سه محور یا سه مولفه یا ویژگی (میانگین، روند و تغییرات فصلی) در مدل سری زمانی هولت وینترز وجود دارد، آن را گاهی به نام هموارسازی نمایی سه‌تایی (Triple Exponential Smoothing) نیز می‌شناسند. در چنین مدلی، پیش‌بینی مقدار آینده توسط ترکیب این سه مولفه، صورت می‌پذیرد. چنین مدلی دارای چندین پارامتر است. این گروه از پارامترها در این مدل با $$\alpha, \beta, \gamma$$ شناخته می‌شوند. به این ترتیب طول دوره تغییرات فصلی و تعداد دوره‌های تغییرات فصلی نیز به عنوان پارامترهای مدل هولت وینترز محسوب می‌شوند.

همانطور که می‌دانید، تغییرات فصلی، یک دوره ثابت از زمان است که به طور کامل داده‌های سری زمانی در آن تکرار می‌شوند. شاید به نظر برسد که داده‌های این سری زمانی، به صورت روزانه تکرار می‌شوند و مثلا در ساعت ۴ بعد از ظهر هر روز بیشترین درصد درخواست‌های تاکسی اینترنتی ثبت شده است. ولی از آنجایی که در روزهای پایانی هفته چنین وضعیتی وجود ندارد، نمی‌توان این تغییرات را به صورت فصل با دوره زمانی روزانه در نظر بگیریم. در چنین وضعیتی بهتر است، دوره تغییرات فصلی را به صورت هفتگی محاسبه کرد.

نکته: ممکن است در یک مدل سری زمانی، احتیاج به پیش‌بینی داده‌های آینده برای مثلا یک ساعت بعد داشته باشید. در این حالت اگر می‌خواهید مدلی‌ پیش‌بین برای هفته‌های آینده را برحسب ساعت داشته باشید باید مدلی با طول فصل ۱۶۸ ساعت و دوره‌های ۱ ساعته ایجاد کنید.

شکل ساده (بدون روند و تغییرات فصلی) مدل سری زمانی هولت وینترز به صورت زیر است:

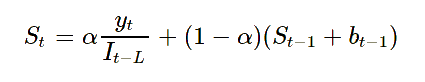
که در آن $$y_t$$ مشاهده مربوط به زمان $$t$$ و $$S_t$$ مشاهده هموار شده در زمان $$t$$‌ است. همانطور که در این مدل مشاهده می‌کنید، فقط پارامتر $$\alpha$$ حضور داشته و هر مشاهده به صورت ترکیب خطی از نقطه قبلی ($$S_{t-1}$$) دیده می‌شود. از طرفی $$I$$ نیز شاخص تغییرات فصلی (Seasonal Index) نامیده شده و $$L$$ نیز طول دوره تغییرات فصلی است.

در صورتی که مدل دارای روند هم باشد شکل مدل به صورت زیر خواهد بود.

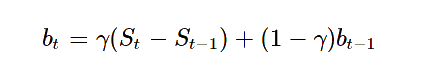
همانطور که مشخص است پارامتر گاما ($$\gamma$$) نیز در مدل اضافه شده است. در نهایت مدلی که به همراه تغییرات فصلی ارائه می‌شود به صورت زیر خواهد بود.

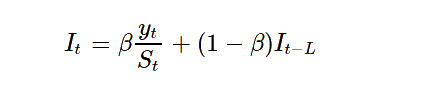
به منظور پیش‌بینی در مدل هولت وینترز، از فرمول زیر کمک می‌گیریم.

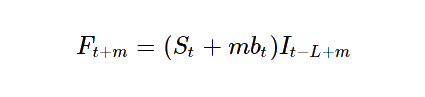
قسمت پیچیده در مدل هولت وینترز، درک روش و کارکرد آن و همچنین حدس نقاط اولیه است که برای برآورد پارامترهای آن احتیاج دارید. در نتیجه ابتدا نحوه محاسبات در این مدل را به صورت دستی انجام می‌دهیم، سپس با استفاده از زبان برنامه‌نویسی و محاسباتی R، کدها و کتابخانه‌هایی را معرفی می‌کنیم که به انجام این امر کمک می‌کنند.

در اغلب توابعی که به منظور برازش مدل سری زمانی هولت وینترز وجود دارند، برای بالا بردن دقت و سرعت برآورد پارامترهای مدل، لازم است که حدس‌های اولیه و تعداد داده‌های خاصی را داشته باشید. برای این موضوع به نکات زیر دقت کنید.

• هنگامی که می‌خواهید مدل هولت وینترز با تغییرات فصل را به صورت کامل داشته باشید، باید داده‌های مربوط به حداقل یک دوره تغییرات فصلی را به مدل ارائه دهید تا شاخص $$I_{t-L}$$ تعیین شود.
• یک مجموعه داده کامل تغییرات فصلی، شامل $$L$$ دوره است. به این ترتیب برای هر دوره با طول $$L$$ باید یک فاکتور روند (Trend Factor) محاسبه شود. بنابراین بهتر است تعداد داده‌های مربوط به تغییرات فصلی برابر $$2L$$ باشند.
• پارامتر $$b$$ به عنوان مقدار اولیه به صورت زیر محاسبه می‌شود.

$$\large b= \dfrac{1}{L}\big(\dfrac{y_{L+1}-y_1}{L}+\dfrac{y_{L+2}-y_2}{L}+\ldots+\dfrac{y_{L+L}-y_L}{L}\big)$$

مقادیر اولیه برای شاخص تغییرات فصلی نیز طی گام‌های زیر بدست می‌آید.

• میانگین را برای هر دوره فصلی محاسبه کنید. برای مثال فرض کنید داده‌های مربوط به ۶ سال در اختیارتان است. با توجه به این که هر سال (تغییرات فصلی) شامل ۴ دوره است. محاسبات به صورت زیر خواهد بود.

$$\large A_p=\dfrac{\sum_{i=1}^4 y_i}{4}, p =1,2,\ldots,6$$

• هر یک از مشاهدات را برای مقدار $$A_p$$‌ مربوطه (یعنی میانگین دوره خودش) تقسیم کنید.

• در آخرین گام نیز محاسبات را برای مقادیر اولیه شاخص فصلی، به شکل زیر انجام دهید.

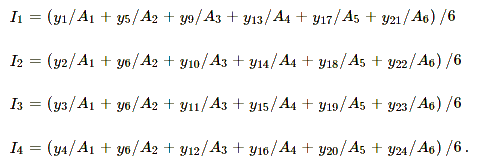
روند پیش‌بینی سری زمانی به روش مدل هولت وینترز

معادلات و تکنیک‌های پیچیده‌ای برای مدل‌سازی در روش هولت وینترز وجود دارد ولی در اینجا به خاطر ساده‌سازی، فقط به مفاهیم و چگونگی عملیات می‌پردازیم و از محاسبات پیچیده دوری می‌کنیم. ابتدا یک مدل ساده را در نظر گرفته سپس با افزایش پارامترهای مدل، آن را کامل‌تر می‌کنیم.

فیلم آموزش متلب با نگرش تحلیل آماری، تحلیل سری های زمانی و داده های مکانی در فرادرس

کلیک کنید

مدل هولت وینترز بدون روند

داده‌های سری زمانی زیر را در نظر بگیرید. مقادیر در بازه زمان ۰ تا ۲۰، یا صفر هستند یا ۱، در نتیجه با مقادیر دو وضعیتی مواجه هستیم.

کدهایی که برای تولید این مجموعه داده لازم است، در ادامه قابل مشاهده‌اند. همانطور که می‌بینید، دوره تغییرات فصلی در این داده‌ها برابر با ۵ واحد زمانی است. پس هر نقطه با نقطه‌ای که ۵ واحد زمانی با آن فاصله دارد، یکسان است.

1<-seq(1,20,1)
2for (i in x){
3  x[i]=0
4if ((i-2)%%5 ==0){
5     x[i] =1
6}
7}
8plot.ts(x,ylab="value",main="")
9points(x)

همچنین مشخص است که داده‌ها به صورت توالی‌هایی از مقادیر $$0,1,0,0,0$$ ساخته شده‌اند. برای پیش‌بینی مقادیر این دنباله یا سری زمانی در آینده می‌خواهیم از پیش‌بینی سری زمانی مدل هولت وینترز استفاده کنیم.

به یاد دارید که یکی از مولفه‌های مدل هولت وینترز، روند (Trend) است. اگر پارامتر مربوط به مولفه روند را صفر در نظر بگیریم، این مولفه از مدل حذف خواهد شد در نتیجه مدل ساده‌تر خواهد بود. همانطور که در داده‌ها نیز مشخص است،‌ مولفه روند در این سری زمانی وجود ندارد.

ابتدا اجازه دهید که میانگین داده‌ها را محاسبه کرده و تغییر مشاهدات حول میانگین را بررسی کنیم. به سادگی دیده می‌شود که میانگین برابر است با ۰٫۲، زیرا:

$$\large \bar{X} = \dfrac{0+1+0+0+0}{5}=0.2$$

خطی به موازات محور افقی به ارتفاع 0٫2 از محور عمودی ترسیم می‌کنیم تا معرف میانگین باشد. به این ترتیب نمودار به صورت زیر درخواهد آمد.

حال فاصله مشاهدات را از مقدار میانگین، مورد بررسی قرار می‌دهیم. این عمل در تصویر زیر به خوبی نمایش داده شده است. توالی این فاصله‌ها، مطابق با جدول زیر خواهد بود.

پس از این به بعد می‌توانیم به جای مشاهدات اصلی از توالی $$-0.2,0.8,-0.2,-0.2,-0.2$$ استفاده کنیم و به راحتی می‌توانیم با اضافه کردن 0٫2 به این مقادیر، به داده‌های اصلی برسیم.

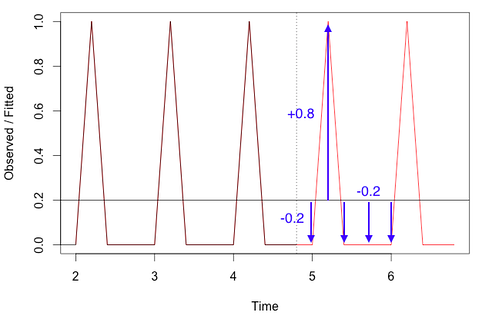
به این ترتیب پیش‌بینی مقادیر آینده مدل را می‌توان با اضافه کردن مقدار ثابت به توالی های گذشته و به کمک تغییرات فصلی با مقدار دوره ۵، بدست آورد.

وجود روند در مدل هولت وینترز

حال برای داده‌های قبلی یک روند افزایشی در نظر می‌گیریم. به این ترتیب میانگین دیگر برحسب زمان ثابت نخواهد بود. بنابراین می‌توان تغییرات را حول یک خط با شیب ثابت در نظر بگیریم. در تصویر زیر نمونه‌ای از چنین مدلی را مشاهده می‌کنید.

برنامه نوشته شده در زیر برای تولید این سری زمانی در زبان برنامه‌نویسی R آورده شده. همانطور که می‌بینید به هر مقدار از مشاهدات، مقداری به عنوان روند اضافه شده است.

1x<-seq(1,20,1)
2trend=50
3for (i in x)
4  {
5  x[i]=0 +i/trend
6  if ((i-2)%%5 ==0)
7    {
8    x[i] =1+i/trend
9    }
10  }
11plot.ts(x,ylab="value",main="")
12points(x)

به این ترتیب به نظر می‌رسد که همه نقطه‌های سری زمانی در بازه‌های مشخصی، روی یک خط مورب با شیب trend (یا معکوس آن) قرار دارند. این خطوط روند، این امکان را می‌دهند که براساس گذشته، آینده را پیش‌بینی کنیم.

مدل هولت وینترز بدون توجه به تغییرات فصلی

از قبل می‌دانیم که تغییرات داده‌ها برحسب زمان دارای یک چرخه یا تغییرات مشخص است بطوری که مقدار هر نقطه در ۵ دوره زمانی بعد،‌ تکرار می‌شود. اگر این شرط از قبل به ما اطلاع داده نشود، پیش‌بینی‌ها چگونه خواهد بود؟

در تصویر زیر با فرض اینکه از وضعیت تغییرات فصل اطلاعی نداریم، عمل پیش‌بینی را انجام داده‌ایم. همانطور که مشاهده می‌کنید، مقادیر آینده با خطای بسیار زیادی برآورد شده‌اند و عملا برای استفاده در آینده مناسب نیستند. در تصویر زیر، تصور شده است که طول دوره تکرار یا تغییرات فصلی براساس تکرار شش دوره زمانی است.

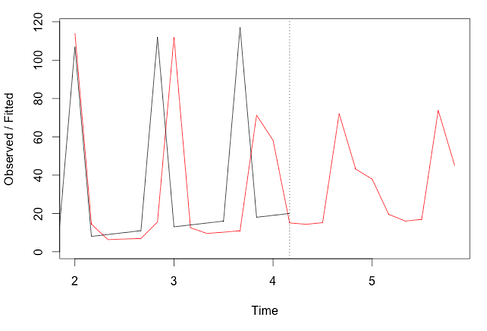
بنابراین تعیین پارامترهای مدل هولت وینترز، از اهمیت زیادی برخوردار است. در ادامه به بررسی روش تخمین پارامترهای مدل هولت وینترز خواهیم پرداخت.

برآورد پارامترهای مدل هولت وینترز

انتخاب مقدار پارامتر برای تغییرات فصلی، یک مسئله مشکل در سری زمانی است. بخصوص زمانی که این پارامتر با پارامترهای دیگر مانند روند نیز مخلوط شده باشد.

البته یکی از روش‌ها استفاده از حدس و گمان برای پارامترهای مدل است ولی این کار ممکن است زمان و هزینه‌های زیادی داشته باشد. به همین دلیل روش‌هایی دیگری مانند یادگیری ماشین (Machine Learning) و تبدیل فوریه (Fourier Transformation) به کار می‌آید. حتی ممکن است برآورد پارامترها بوسیله مدل‌سازی براساس مقادیر مختلف برای تغییرات فصلی صورت گرفته و مناسب‌ترین مدل با توجه به میانگین مربعات خطا، مشخص شود.

در کد زیر با استفاده از زبان برنامه‌نویسی R و تابع HoltWinters برای سه مجموعه داده، پیش‌بینی سری زمانی صورت گرفته است. ابتدا تغییرات فصلی و روند را نادیده گرفته و به کمک این تابع فقط یک مدل سری زمانی ساده را با استفاده از هموارسازی نمایی (میانگین متحرک) برازش می‌کنیم.

داده‌های این مجموعه مربوط به جمعیت کشور آمریکا بوده که براساس یک نوفه (Noise) با انحراف استاندارد ۵ و میانگین جمعیت در هر سال، تغییر یافته است.

1## Exponential Smoothing
2x <- uspop + rnorm(uspop, sd = 5)
3m1 <- HoltWinters(x, gamma = FALSE, beta = FALSE)
4plot(m1)
5m1

نتیجه اجرای این دستورات به صورت زیر خواهد بود.

1Holt-Winters exponential smoothing without trend and without seasonal component.
2
3Call:
4HoltWinters(x = x, beta = FALSE, gamma = FALSE)
5
6Smoothing parameters:
7 alpha: 0.999921
8 beta : FALSE
9 gamma: FALSE
10
11Coefficients:
12      [,1]
13a 200.6411

همانطور که مشخص است پارامترهای $$\beta$$ و $$\gamma$$ صفر در نظر گرفته شده و فقط پارامتر $$\alpha$$ که با alpha مشخص شده، برآورد شده که برابر با 0٫9999 است. از طرفی میانگین (عرض از مبدا) نیز 200٫641 بدست آمده که متوسط جمعیت آمریکا تا سال 1970 است. نموداری که در ادامه مشاهده می‌کنید، پیش‌بینی مقدار جمعیت را برای دوره‌های بعدی نشان می‌دهد. هرچند پیش‌بینی به خوبی صورت گرفته ولی با اضافه کردن پارامترهای بیشتر می‌توان به دقت مناسب‌تری رسید.

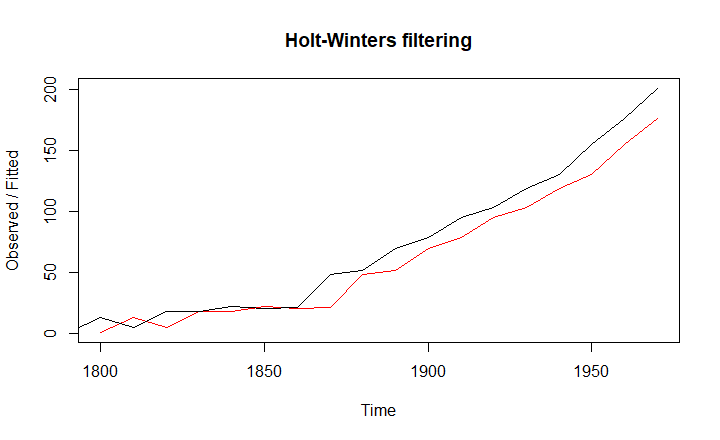
حالا زمانی را در نظر بگیرید که عامل روند را هم در مدل دخیل کنیم. کدهای زیر به این منظور نوشته شده‌اند. همانطور که مشخص است پارامتر $$\beta$$ نیز که با beta‌ مشخص شده، در مدل حضور دارد.

1## Non-Seasonal Holt-Winters
2m2 <- HoltWinters(x, gamma = FALSE)
3lines(fitted(m2)[,1], col = 3)
4m2

خروجی به صورت زیر است.

1Holt-Winters exponential smoothing with trend and without seasonal component.
2
3Call:
4HoltWinters(x = x, gamma = FALSE)
5
6Smoothing parameters:
7 alpha: 1
8 beta : 0
9 gamma: FALSE
10
11Coefficients:
12       [,1]
13a 200.64300
14b  11.80923

به این ترتیب شیب خط مدل هولت وینترز برابر است با b=11.80923 و عرض از مبدا نیز a=200.643 خواهد بود. نموداری که در ادامه شاهد هستید، داده‌های اصلی را به همراه دو روش برآورد مدل هولت وینترز نشان می‌دهد.

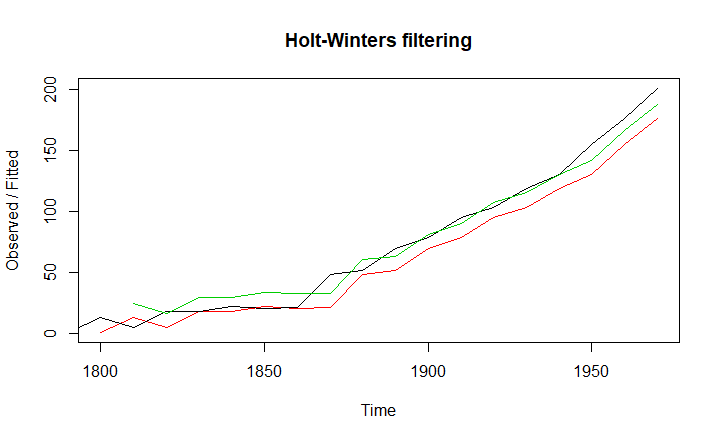
به نظر می‌رسد که استفاده از پارامتر beta روند را به خوبی پیش‌بینی کرده و نتایج بهتری را نشان می‌دهد.

در گام آخر می‌خواهیم به واسطه یک سری داده که دارای تغییرات فصل است، پارامترهای مدل هولت وینترز را برآورد کنیم. مجموعه داده مورد نظر در اینجا، میزان دی‌اکسید کربن در هوا است که به تفکیک ماه از سال ۱۹۵۹ تا ۱۹۹۷، جمع‌آوری شده است.

نکته: این مجموعه داده در R وجود داشته و احتیاجی به بازگذاری آن نیست.

1## Seasonal Holt-Winters
2m <- HoltWinters(co2)
3plot(m)
4m
5plot(fitted(m))

خروجی پس از اجرای این دستورات به صورت زیر خواهد بود.

1Holt-Winters exponential smoothing with trend and additive seasonal component.
2
3Call:
4HoltWinters(x = co2)
5
6Smoothing parameters:
7 alpha: 0.5126484
8 beta : 0.009497669
9 gamma: 0.4728868
10
11Coefficients:
12           [,1]
13a   364.7616237
14b     0.1247438
15s1    0.2215275
16s2    0.9552801
17s3    1.5984744
18s4    2.8758029
19s5    3.2820088
20s6    2.4406990
21s7    0.8969433
22s8   -1.3796428
23s9   -3.4112376
24s10  -3.2570163
25s11  -1.9134850
26s12  -0.5844250

نمودار اول نیز مربوط به داده‌های اصلی و مدل برازش شده است و تصاویر بعدی نیز مدل‌های مختلف توسط روش هولت وینترز را نشان می‌دهد.

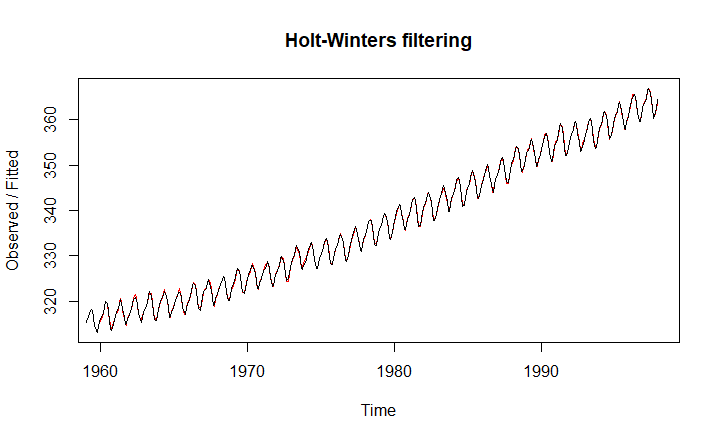
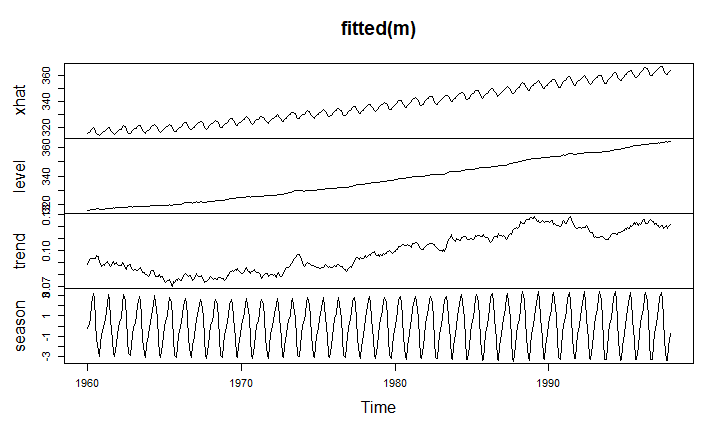
برای اینکه روند حل مسئله را بدون استفاده از برنامه‌های و توابع نرم‌افزارهای محاسبات آماری نیز بیاموزیم به یک مثال خواهیم پرداخت.

نکته: مجموعه داده‌های به کار رفته در این مدل‌ها در محیط برنامه‌نویسی R وجود دارند و احتیاجی به بارگذاری آن‌ها نیست.

مثال

در این مثال، روش تک،‌ دوتایی یا مضاعف و  همچنین سه‌تایی در هموارسازی نمایی یا مدل هولت وینترز را با یکدیگر مقایسه می‌کنیم. یک مجموعه داده که شامل ۲۴ مشاهده در ۶ سال با دوره ۴ ماهه است جمع‌آوری شده است. فایل مربوط به این مجموعه داده را با قالب متنی از اینجا می‌توانید دریافت کنید.

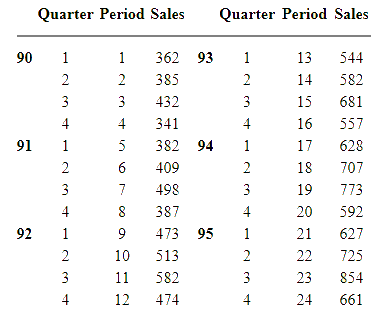
طبق مطالبی که در مورد نقاط اولیه گفته شد، خواهیم داشت:

$$\large L=4$$

و

$$\large b_1=\dfrac{1}{4}\big[\big(\dfrac{y_5-y_1}{4}\big)+\big(\dfrac{y_6-y_2}{4}\big)+\big(\dfrac{y_7-y_3}{4}\big)+\big(\dfrac{y_8-y_4}{4}\big)\big]=$$

$$\large \dfrac{1}{4}\big[\big(\dfrac{382-362}{4}\big)+\big(\dfrac{409-385}{4}\big)+\big(\dfrac{498-432}{4}\big)+\big(\dfrac{387-341}{4}\big)\big]=$$

$$\large \dfrac{5+6+16.5+11.5}{4}=9.75$$

همچنین مقادیر اولیه برای شاخص فصلی نیز به صورت زیر خواهد بود.

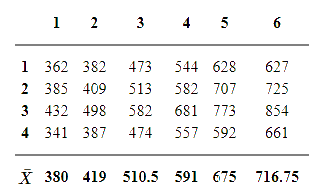
اینک به کمک توابع گفته شده در R می‌توانید محاسبات مربوط به مدل‌سازی را در حالت‌های یک، دو و سه پارامتری به کمک مدل هولت وینترز اجرا کنید.

خلاصه و جمع‌بندی

در سری زمانی نمی‌دانید در آینده چه داده‌ای ظاهر خواهد شد ولی می‌توانید براساس گذشته، برای فرآیند تصادفی، مدل مناسبی را ایجاد کنید. از آنجایی که تشخیص رفتار داده‌ها سخت است، مدل‌سازی براساس داده‌های سری زمانی می‌تواند واقعاً پیچیده باشد، اما بسیاری از تکنیک‌ها و روش‌های ساده و کارآمد مانند EWMA یا (Exponentially Weighted Moving Average) با اضافه کردن کمی زمان و هزینه، می‌توانند بهترین نتیجه را بوجود آورند.

فیلم مجموعه آموزش پیش‌‌ بینی و تحلیل سری‌‌ های زمانی – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

البته استفاده از  تکنیک‌های پیچیده‌تر برای موارد بسیار خاص مناسب بوده و پیش‌بینی را با دقت بیشتری انجام می‌دهند ولی با پیچیده‌تر شدن مدل، هزینه‌های محاسباتی نیز افزایش می‌یابد. در این نوشتار با هموار سازی و مدل هولت وینترز آشنا شدیم و براساس نمودارها و روابطی که معرفی کردیم، ساختار آن را آموزش دادیم.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب سری زمانی هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌‌ بینی و تحلیل سری‌‌ های زمانی
• آموزش تحلیل و پیش بینی سری های زمانی
• مجموعه آموزش‌های SPSS
• ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده
• سری زمانی در علم داده — از صفر تا صد
• تابع خودهمبستگی (Autocorrelation Function) — مفاهیم و کاربردها

^^