مدل سازی تابش خورشید | پیاده سازی در متلب
انرژی خورشیدی بخشی از گرما و نور حاصل از تابش خورشید است که برای کاربردهای مختلف در سطح زمین در دسترس است. از این کاربردها میتوان به برانگیختن الکترونهای یک سلول فتوولتائیک، فراهم کردن انرژی برای فرایندهای طبیعی مانند فتوسنتز یا گرم کردن اشیاء اشاره کرد. این انرژی مجانی، پاک و فراوان در طول سال در بیشتر نقاط در دسترس است و به دلیل هزینه سوختهای فسیلی و آلودگی هوای ناشی از آنها مورد توجه قرار گرفته است. انرژی موجود در تابش خورشید شامل دو قسمت است: تابش فرازمینی (Extraterrestrial Solar Radiation) که بالاتر از جوّ است و تابش کلی (Global Solar Radiation) که در سطح زیر جوّ قرار دارد.


تابش کلی معمولاً توسط آفتابسنجها (پیلومومترها)، حسگرهای خورشیدی، تابهسنجها (اکتینوگرافها) یا گرماسنجها اندازهگیری میشود. این ابزارهای اندازهگیری معمولاً در محلهای خاصی از مناطق مشخص نصب میشوند. با توجه به هزینه بالای این دستگاهها، امکان نصب آنها در بسیاری از محلها وجود ندارد. از سوی دیگر، این دستگاههای اندازهگیری، تلرانس قابل توجه و دقت کمی دارند؛ در نتیجه ممکن است موجب ثبت اشتباه دادهها یا از دست رفتن آنها شوند. مدلسازی منبع خورشیدی با استفاده از علم نجوم و اصول هندسه راهحل مناسبی برای این رفع مشکل است. همچنین، میتوان از مقدار تابش اندازهگیری شده، برای تشکیل مدلهای تابش بهره برد. این مدلها روابط ریاضی بین تابش خورشید و متغیرهای هواشناسی مانند دمای محیط، رطوبت و نرخ تابش را توصیف میکنند. همچنین میتوان از این مدلها برای پیشبینی تابش در مکانهایی استفاده کرد که دستگاه اندازهگیری انرژی خورشیدی نصب نشده است.
مدلسازی موقعیت خورشید
همانطورکه میدانیم، زمین در یک مدار بیضوی اطراف خورشید گردش میکند. شکل ۱، مدار چرخش زمین به دور خورشید را نشان میدهد.
مدت زمان هر چرخش زمین به دور خورشید حدود 8766 ساعت، تقریباً برابر با 365٫242 روز است.
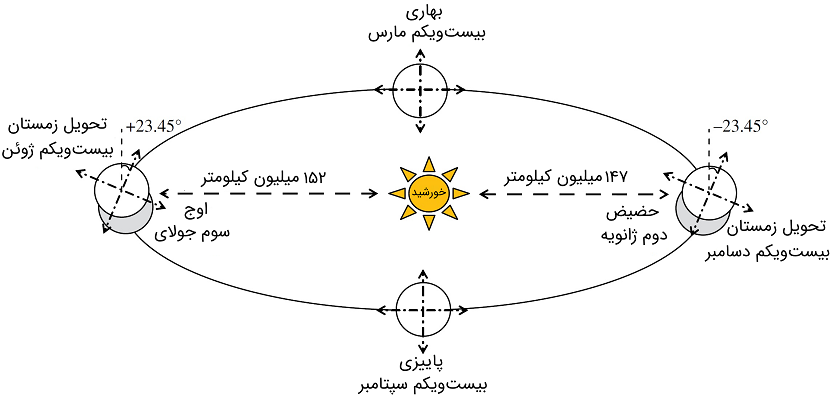
نقاط منحصر به فردی در مدار شکل ۱ وجود دارد. تحویل زمستان در 21 دسامبر رخ میدهد که در آن، زمین تقریباً 147 میلیون کیلومتر از خورشید فاصله دارد. از سوی دیگر، روز تحویل تابستان که در 21 ژوئن اتفاق میافتد، زمین حدود 152 میلیون کیلومتر از خورشید دور است. برای بررسی دقیقتر میتوان گفت زمین در 2 ژانویه به خورشید نزدیک است (147 میلیون کیلومتر) که این نقطه بهنام «حضیض» (Perihelion) شناخته میشود. نقطهای که زمین از خورشید دورتر است (152 میلیون کیلومتر)، «اوج» (Aphelion) نامیده میشود و در 3 جولای رخ میدهد.
همانطورکه در شکل ۲ دیده میشود، برای ناظری که در نقطه مشخصی از زمین ایستاده است، موقعیت خورشید با دو زاویه اصلی یعنی زاویه فراز (Altitude angle) و زاویه سمت (Azimuth angle) تعیین میشود.
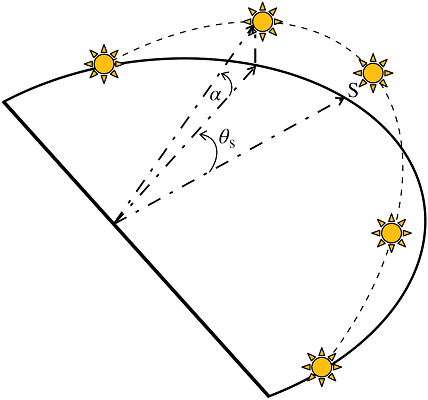
در شکل 2، زاویه فراز، زاویه ارتفاع خورشید در آسمان است که نسبت به افق اندازهگیری میشود. زاویه فراز را میتوان با
بیان کرد که در آن، «عرض جغرافیایی» (Latitude) محل، «زاویه میل» (Angle of declination) و «زاویه ساعت» (Hour angle) است.
زاویه میل، زاویه بین بردار زمین-خورشید و صفحه استوا است (شکل ۳ را ببینید) و به صورت زیر محاسبه میشود (نتایج به درجه و آرگومان توابع مثلثاتی برحسب رادیان است):
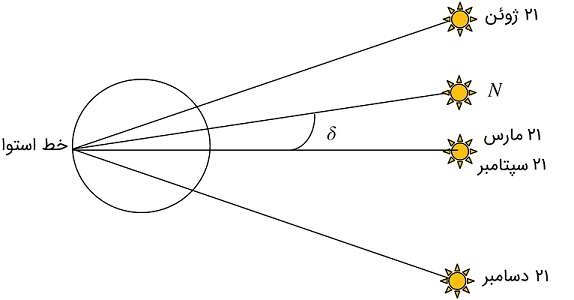
زاویه ساعت ، جابهجایی زاویهای خورشید از نقطه محلی است و با
به دست میآید که در آن، AST «زمان ظاهری یا حقیقی خورشیدی» (True Solar Time) است و با حرکت ظاهری روزانه خورشید تعیین میشود. زمان ظاهری بر اساس روز ظاهری محاسبه میشود و فاصله زمانی بین دو بازگشت متوالی خورشید به نصفالنهار محلی است. زمان ظاهری با
تعیین میشود که در آن، LMT «زمان نصفالنهار محلی» (Local Meridian Time) و LOD «طول جغرافیایی» (Longitude) و LSMT «زمان نصفالنهار استاندارد محلی» (Local Standard Meridian Time) و EOT یک «معادله زمانی» است.
LSMT نصفالنهار مرجع است که برای یک منطقه زمانی خاص استفاده میشود و مشابه نصفالنهار اولیهای است که برای زمان میانگین گرینویچ به کار میرود. LSMT را میتوان با رابطه زیر محاسبه کرد:
EoT اختلاف بین زمانهای میانگین و ظاهری خورشید است که هر دو در طول جغرافیایی خاصی در یک لحظه واقعی رخ میدهند. EoT توسط
مشخص میشود و در آن میتوان را با رابطه زیر محاسبه کرد:
از طرف دیگر، زاویه سمت که در شکل ۲ دیده میشود، جابهجایی زاویهای خط مرجع خورشید از محور منبع است. زاویه سمت را میتوان با استفاده از رابطه زیر به دست آورد:
مثال 1
برنامهای در متلب بنویسید که زاویههای فراز و سمت را در ساعت 13:12 روز دوم جولای برای شهر کوالالامپور محاسبه کند.
حل: بخشهای اصلی برنامه به صورت زیر است:
- مختصات مکان (طول و عرض جغرافیایی)، شماره روز و زمان میانگین محلی را وارد کنید.
- زاویه میل، معادله زمانی و LMST را محاسبه کنید.
- AST و زاویه ساعت را محاسبه کنید.
- زاویه فراز را بهدست آورید.
- زاویه سمت را محاسبه کنید.
- نتایج را رسم کنید.
کد متلب این مثال به صورت زیر است:
پاسخ: ؛ .
مثال 2
برنامه نوشته شده مثال 1 را برای محاسبه نمودار زاویههای فراز و سمت (هر 5 دقیقه) کل روز خورشیدی دوم جولای شهر کوالالامپور اصلاح کنید.
حل: روز خورشیدی بهعنوان طول مدت طلوع تا غروب خورشید تعریف میشود. بنابراین، باید زاویه فراز و زاویه سمت را برای هر ساعت از طلوع تا غروب خورشید محاسبه کرد. میتوان زاویههای طلوع و غروب خورشید را برابر در نظر گرفت و به صورت زیر به دست آورد:
در عین حال، زمان خورشید هر زاویه ساعت را میتوان با بازنویسی معادله (۳) به صورت زیر محاسبه کرد:
اگر بخواهیم زمان طلوع خورشید را محاسبه کنیم، علامت معادله (۱۰) باید منفی باشد و در صورتی که قصد محاسبه زمان غروب آفتاب را داشته باشیم باید آن را مثبت قرار دهیم. پس از آن، بخش اصلی ساختار برنامه را میتوان به شرح زیر نوشت:
- مختصات مکان (طول و عرض جغرافیایی) و شماره روز را وارد کنید.
- زاویه میل را حساب کنید.
- زاویههای ساعت طلوع و غروب خورشید را محاسبه کنید.
- AST طلوع و غروب را محاسبه کنید.
- معادله زمانی و LMST را محاسبه کنید.
- زمانهای واقعی طلوع و غروب را بهدست آورید.
- یک حلقه با شروع از طلوع و پایان غروب خورشید با اندازه گام 5 دقیقه تعریف کنید.
- زمان خورشید و زاویه ساعت را در هر گام محاسبه کنید.
- زاویه فراز را در هر گام محاسبه کنید.
- زاویه سمت را در هر گام محاسبه کنید.
- زاویههای فراز و سمت محاسبه شده را در آرایهها ذخیره کنید.
- نتایج را رسم کنید.
برنامه متلب این مثال به صورت زیر است:
پاسخ: شکل ۴.
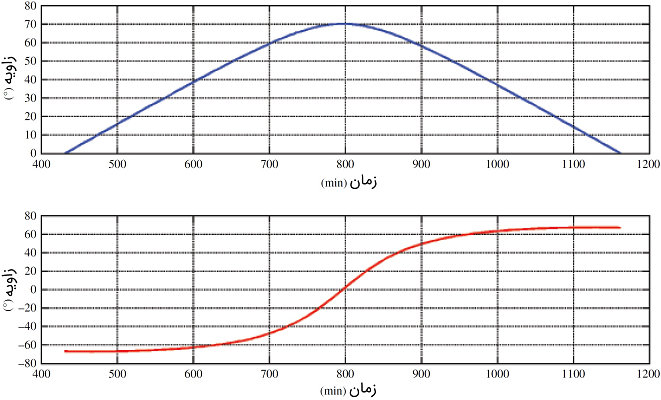
مدلسازی تابش فرازمینی
اولین گام در مدلسازی منبع خورشیدی، تخمین تابش خورشید است. همانگونه که میدانیم، انرژی تابشی هر جسم را میتوان به صورت تابعی از دمای آن توصیف کرد. راه متداول برای تخمین انرژی تابشی یک جسم، مقایسه آن با یک جسم سیاه است. جسم سیاه به عنوان یک گسیلنده و یک جذب کننده کامل تعریف شده است. با جذب کامل میتوان تمام انرژی دریافت شده را با هر بازتابی جذب کرد، در حالی که یک گسیلنده کامل، انرژی را بیش از هر جسم دیگری منتشر میکند. قانون پلانک، طول موج منتشر شده جسم سیاه را در یک دمای خاص به صورت زیر توصیف میکند:
که در آن، کلِ تابش در واحد سطح با نرخ انتشار جسم سیاه ()، دمای مطلق جسم سیاه () و طول موج () است.
مثال ۳
برنامهای بنویسید که قدرت انتشار طیفی یک جسم سیاه 228 کلوین را در محدوده طول موجهای 1 تا 60 میکرومتر حساب کند. پس از آن قدرت انتشار را برای طول موج 20 و 30 میکرومتر محاسبه کنید.
حل: بخش اول این مثال را میتوان به سادگی با استفاده از معادله (۱۱) و محاسبه مقدار آن برای محدوده طول موج مورد نظر به صورت زیر حل کرد:
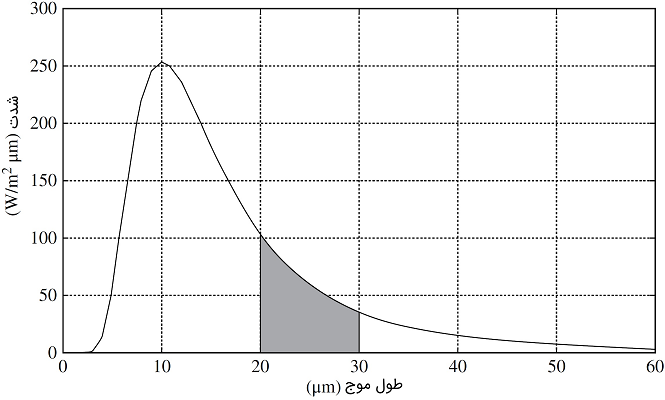
برای محاسبه توان انتشار بین طولموج 20 و 30 میکرومتر، میتوان بخش سایه شکل ۵ را به صورت زیر محاسبه کرد:
که پیادهسازی آن در متلب به صورت زیر است:
پاسخ: .
دمای درون خورشید حدود 15 میلیون کلوین است، در حالی که دمای سطح آن بسیار سردتر بوده و تقریباً 5778 کلوین (5505 درجه سانتیگراد) است. بنابراین، تابشی که از سطح خورشید منتشر میشود، یک توزیع طیفی مطابق با پیشبینی قانون پلانک برای یک جسم سیاه است. مساحت کل زیر منحنی جسم سیاه تا است که مقدار تابش خورشید فقط در خارج از جو زمین است. این مقدار تابش، «ثابت خورشید» (Solar constant) () نامیده میشود، گرچه به دلیل مدار بیضوی زمین، قطر آن و تغییر شرایط در فعالیت خورشید، کاملاً ثابت نیست. مقدار پیشنهادی ثابت خورشیدی از سوی بسیاری از محققان، است.
مقدار تابش در خارج از جو زمین، به دلیل چرخش زمین حول خورشید تغییر میکند. از این رو باید فاصله بین خورشید و زمین را در مدلسازی تابش فرازمینی در نظر گرفت. بنابراین، تابش فرازمینی () با رابطه (۱۳) بیان میشود:
که در آن، فاصله میانگین و فاصله لحظهای بین خورشید و زمین است. فاصله لحظهای بین خورشید و زمین به روزِ سال یا شماره روز بستگی دارد. در واقع، تقریبهای مختلفی برای عامل () وجود دارد. یک تقریب توصیه شده به صورت زیر است:
با جایگذاری معادله (۱۴) در معادله (۱۳)، میتوان تابش فرازمینی واحد زمان را که به واحد متر مربع سطح میتابد با رابطه زیر بیان کرد:
با این حال، مفهومی که اغلب در مدلهای تابش خورشید استفاده میشود، این است که تابش فرازمینی به یک سطح افقی میتابد. یک سطح تخت را در خارج از جو زمین و به موازات سطح زمین در زیر آن در نظر بگیرید. هنگامی که این سطح با خورشید مواجه میشود (با یک پرتوی مرکزی، نرمال است)، تابش روی آن است که حداکثر تابش خورشیدی در آن فاصله است. اگر سطح نسبت به خورشید نرمال نباشد، تابشی خورشیدی که روی آن فرود میآید، با کسینوس زاویه بین نرمال سطح و یک پرتوی مرکزی از خورشید کاهش مییابد. این مفهوم در شکل ۶ توضیح داده شده است. در این شکل مشاهده میشود که نرخ انرژی خورشیدی روی هر دو سطح یکسان است. با این حال، مساحت سطح A بزرگتر از تصویر آن، یعنی سطح فرضی B است که به همین دلیل، نرخ انرژی خورشیدی واحد سطح، روی سطح A کمتر از سطح B است.
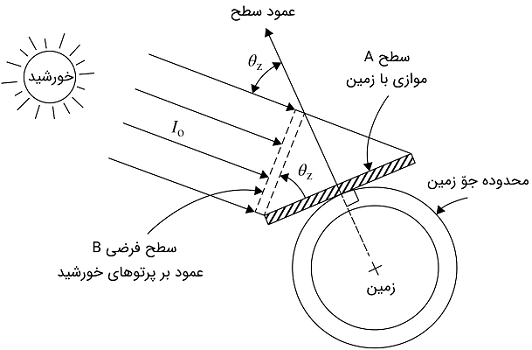
بنابراین، تابش خورشیدی فرازمینی () روی سطح زمین در یک سطح افقی واقع در یک مکان خاص را میتوان از رابطه (۱۶) محاسبه کرد:
که در آن، زاویه اوج خورشید است که مستقیماً از بالا نسبت به مرکز هندسی قرص خورشید اندازهگیری میشود. اندازه زاویه اوج برابر با مقدار فراز است و بنابراین معادله (۱۶) را میتوان به صورت زیر بازنویسی کرد:
در نهایت، کل انرژی خورشیدی فرازمینی () بر حسب به صورت زیر محاسبه میشود:
مثال ۴
برنامهای بنویسید که پروفیل تابش فرازمینی ساعتی را برای شهر نابلس فلسطین در سی و یکم مارس پیشبینی کند.
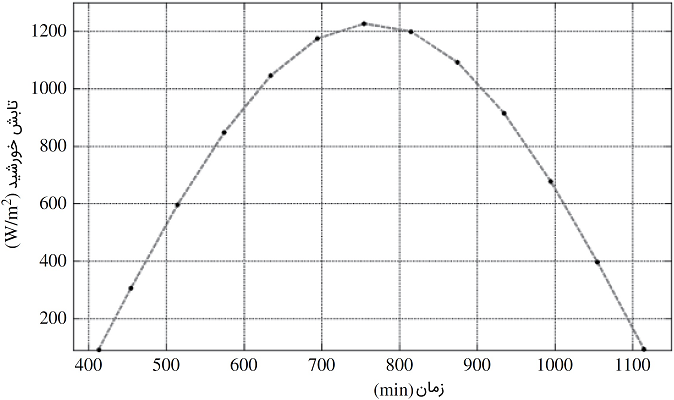
حل: با توجه به معادله (۱۷)، ابتدا باید مقادیر ساعتی زاویه فراز مکان انتخابی را محاسبه کرد (مثال ۲ را ببنید). سپس میتوان مقدار تابش ساعتی را با استفاده از معادله (۱۷) به صورت زیر به دست آورد:
پاسخ: شکل ۷.
مدلسازی تابش زمینی روی یک سطح افقی
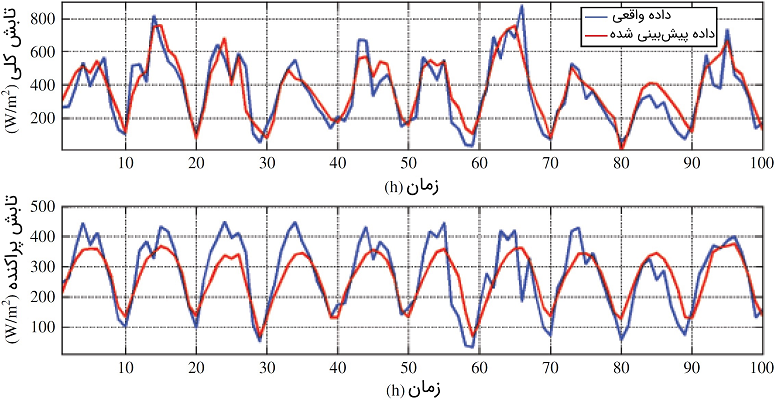
تابش کل ()، تابش موجود در سطح دریا و زیر جو زمین است. تابش کل که روی یک سطح افقی وجود دارد، شامل دو جزء مستقیم یا پرتو (Direct Solar Radiation) و پراکنده (Diffuse Solar Radiation) است. شکل ۸ اجزای تابش خورشیدی را در یک سطح افقی نشان میدهد. تابش مستقیم خورشید ()، پرتویی است که مستقیماً از خورشید ساطع میشود، در حالی که تابش پراکنده خورشید ()، تابشی است که ابرها و ذرات دیگر در آسمان پراکنده میکنند.
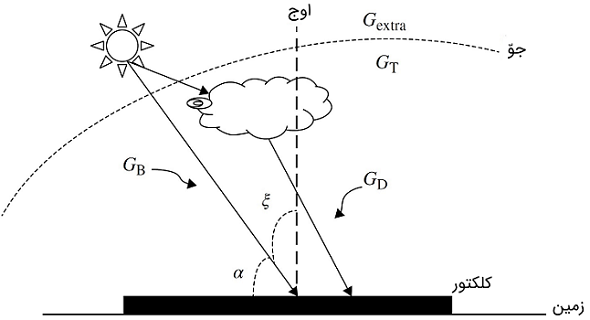
بنابراین میتوان را به شکل زیر توصیف کرد:
وقتی پرتوهای تابش خورشید از جو عبور میکنند، بسیاری از اجزای این پرتوها توسط گازهای آسمان یا مولکولهای هوا جذب، خنثی و پراکنده میشوند. برای یک روز با آسمان صاف، 70 درصد از تابش کلی، تابش مستقیم است. تضعیف این پرتو به دلیل گرد و غبار، آلودگی هوا، بخار آب، ابرها و مه را میتوان نسبتاً راحت مدل کرد. راهحلهای زیادی برای مدلسازی این تضعیف به عنوان تابعی از شماره روز وجود دارد. یکی از این مدلها، مدل اَشری (ASHRAE Model) است که گاهی مدل آسمان صاف نامیده میشود. با این مدل، تابش مستقیم خورشید را که به سطح زمین میرسد () میتوان به صورت زیر نوشت:
که در آن، شار فرازمینی ظاهری و یک عامل بدون بعد است که عمق نوری نامیده میشود. عاملهای و را میتوان به عنوان توابعی از شماره روز بیان کرد:
اکنون میتوان تابش مستقیم جذب شده توسط سطح افقی را به شکل زیر توصیف کرد:
از سوی دیگر، محاسبه تابش پراکنده روی یک کلکتور مسطح افقی، نسبت به محاسبه تابش مستقیم دشوارتر است. تابش ورودی، ممکن است با ذرات جو و بخار آب پراکنده و توسط ابرها منعکس شود. بعضی از تابشها از سطح به آسمان بازتاب و دوباره به زمین پراکنده میشوند. در سادهترین مدلهای تابش پراکنده، فرض میشود که تابش با شدت برابر از تمام جهات به یک محل میرسد؛ به عبارت دیگر، آسمان به صورت همسان در نظر گرفته میشود. بدیهی است که در روزهای مهآلود یا بارانی، آسمان در مجاورت خورشید بسیار درخشانتر از قبل است و اندازهگیریها نیز پدیده مشابهی را در روزهای صاف نشان میدهد، اما این عوارض اغلب نادیده گرفته میشود. در نهایت، تابش پراکنده خورشید را میتوان با رابطه (۲۴) تقریب زد:
مثال ۵
برنامهای در متلب بنویسید که پروفیل تابش پراکنده و کلی یک سطح افقی را در دوم مِی از طلوع تا غروب خورشید برای شهر کویت به صورت ساعتی پیشبینی کند.
حل: برنامه مورد نظر را به دو بخش تقسیم میکنیم: محاسبه زاویه فراز و سپس محاسبه جزء تابش خورشید. بخش اول در مثالهای قبلی مانند مثال ۲ نشان داده شد. برای بخش دوم، برنامه معادلات (۱۹) تا (۲۴) به شرح زیر است:
پاسخ: شکل ۹.
مدلسازی تابش کلی روی یک سطح صاف
اجزای تابش کلی یک کلکتور شیبدار در شکل ۱۰ نشان داده شده است.
علاوه بر تابش مستقیم () و تابش پراکنده ()، مولفه جدیدی بهنام بازتاب تابش خورشیدی (Reflected Solar Radiation) اضافه شده است که تابش سطح شیبدار را شکل میدهد.
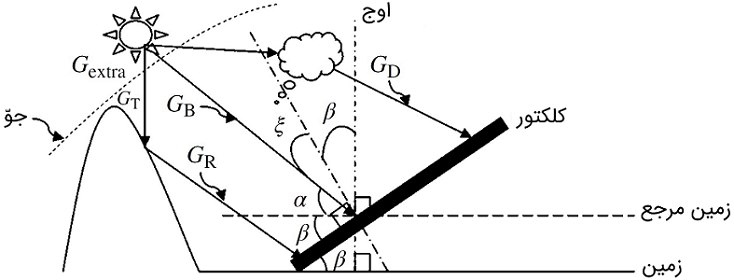
این مؤلفهها را میتوان با رابطه (۲۵) نشان داد:
معادله (۲۵) را میتوان با توجه به مؤلفههای انرژی خورشیدی در یک سطح افقی به صورت زیر بازنویسی کرد:
که در آن، ، و ضرایب هستند و «آلبِدو یا سپیدایی زمین» (Ground Albedo) به معنی درصد بازتاب نور از سطح است. همچنین، نسبت بین انرژی خورشیدی کلی در یک سطح افقی و انرژی خورشیدی کلی روی سطح شیبدار، نسبت بین انرژی خورشیدی پراکنده در یک سطح افقی و انرژی خورشیدی پراکنده سطح شیبدار و عامل انرژی خورشیدی بازتاب شده سطح شیبدار است.
از معادله (۲۶) واضح است که کلید یافتن مؤلفههای انرژی خورشیدی روی سطح شیبدار، تخمین ضرایب ، و است. متداولترین مدل برای محاسبه «مدل لیو و جردن» (Liu and Jordan Model) است که در آن، به صورت زیر محاسبه میشود:
از آنجا که در سطوح در نیمکره جنوبی شیب به سمت استوا است، معادله به صورت زیر نشان داده میشود:
در عین حال، بهترین معادله برای ، رابطه (۲۹) است:
از سوی دیگر، برای مدلهای زیادی ارائه شده که میتوان آنها را در مدلهای همسان و ناهمسان دستهبندی کرد.
مدل خورشیدی همسان، مبتنی بر این فرض است که تابش همسان بدون در نظر گرفتن جهت اندازهگیری، شدت یکسانی دارد و میدان همسان بدون در نظر گرفتن چگونگی ذرات آزمون، عمل میکند. این تابش در همه جهات به صورت یکنواخت از یک منبع نقطهای میتابد که گاهی «تابنده یا رادیاتور همسان» (Isotropic Radiator) نامیده میشود. یکی از مدلهای رایج تابش پراکنده، مدل لیو و جردن با است:
از سوی دیگر، ناهمسان بودن که به معنای وابستگی به جهت است، در مقابل همسان بودن که به معنای خواص یکسان در همه جهات است قرار میگیرد. این را میتوان به عنوان یک تفاوت اندازهگیری در امتداد محورهای مختلف ویژگیهای فیزیکی مواد (جذب، شاخص شکست، چگالی و غیره) تعریف کرد. بنابراین، مدلهای خورشیدی ناهمسان، مبتنی بر این فرض هستند که تابش ناهمسان بسته به جهت اندازهگیری، شدت متفاوتی دارد و در همه جهات، غیریکنواخت میتابد. چند مدل ناهمسان که برای ارائه شدهاند، به صورت زیر هستند:
مثال ۶
برنامهای بنویسید که تابش پراکنده و کلی ساعتی را روی یک سطح شیبدار برای شهر کویت از طلوع تا غروب خوشید در 31 مارس پیشبینی کند.
حل: برنامه متلب این مثال به صورت زیر است:
پاسخ: شکل ۱۱
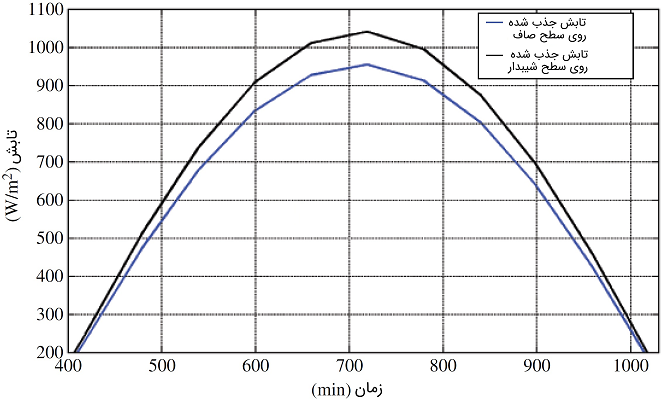
مدلسازی تابش براساس اندازهگیریهای زمین
متغیرهای ورودی که معمولاً برای پیشبینی انرژی کلی در نقاط مختلف مورد استفاده قرار میگیرند نرخ نور (تابش) خورشید، دمای محیط و رطوبت نسبی هستند.
انرژی کلی در یک سطح افقی، میانگین تابش کلی ضرب در زمان روز خورشیدی است. زمان روز خورشیدی () با رابطه (۳۷) محاسبه میشود:
انرژی کلی شدیداً به عاملی به نام نرخ تابش خورشید وابسته است. نرخ تابش بالا، به معنی انرژی زیاد است و برعکس. نرخ خورشید با رابطه (۳۸) داده میشود:
که در آن، تعداد ساعات تابان در یک روز آفتابی است و ابعاد میانگین روزانه اندازهگیری شده با مقادیر برای آسمان صاف تا برای آسمان کاملاً ابری است.
مدلسازی تابش کلی
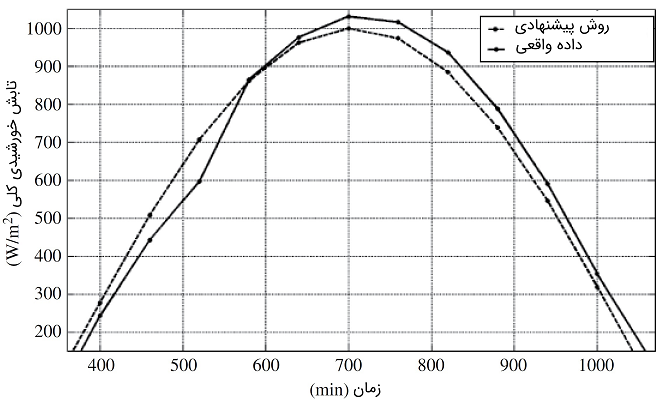
مدلهای زیادی برای مدلسازی انرژی کلی خورشید روی سطح افقی ارائه شده است. به طور کلی، چهار نوع مدل خطی، غیرخطی، فازی و مبتنی بر هوش مصنوعی برای مدلسازی انرژی کلی خورشید وجود دارد. تابش کلی با ساعت خورشیدی رابطه خطی دارد. بنابراین، برای محاسبه انرژی کلی، میتوان یک مدل خطی براساس ساعت خورشید طراحی کرد. یکی از مدلهای متداول در معادله (۳۹) آمده است:
راههای مختلفی برای تعیین ضرایب و به صورت بهینه وجود دارد. اولین مدل تخمین انرژی کلی که به عنوان «مدل آنگستروم» (Angström Model) شناخته میشود، از دادههای مدت تابش خورشید حاصل میشود و مقادیر و را به صورت زیر تعریف میکند:
مثال ۷
با استفاده از نرمافزار متلب، یک مدل خطی برای میانگین ماهیانه تابش خورشیدی براساس اطلاعات جدول زیر بنویسید. فرض کنید زمان خورشیدی برابر با زمان محلی است.
حل: برنامه مربوط به این مثال به صورت زیر است:
پاسخ:
از سوی دیگر، میتوان مدلی را با اضافه کردن یک جمله غیرخطی به مدل آنگستروم به صورت زیر پیشنهاد کرد:
تعدادی از مطالعات نظری نشان داده است که حساسیت خواص پرتوافکنی ابرها نسبت به ساختار فضایی آنها، بر مدت تابش خورشید و در نتیجه، مقدار انرژی کلی اثر میگذارد. بنابراین، در هر فرایند تخمینی، ضروری است که لحظات آماری مرتبه سوم یا بالاتر در نظر گرفته شود. یکی از راههای ادغام این لحظات در مدل، گنجاندن توان سوم متغیر مدت خورشید است:
معمولاً در انرژی و زمان تابش خورشید در طول روز ابهاماتی وجود دارد. برای مقابله با این عدم قطعیت و تخمین مقدار تابش میتوان از الگوریتم «منطق فازی» (Fuzzy logic) استفاده کرد. مزیت اصلی مدل فازی این است که توانایی توصیف دانش را به شیوه توصیفی انسان و در قالب قواعد ساده، تنها با استفاده از متغیرهای زبانی دارد. گزارههای منطقی فازی به صورت عبارتهای اگر-آنگاه هستند، به عنوان مثال:
- اگر مدت تابش نور آفتاب «طولانی» باشد، آنگاه مقدار انرژی خورشیدی «زیاد» است.
- اگر مدت تابش نور آفتاب «کوتاه» باشد، آنگاه مقدار انرژی خورشیدی «کم» است.
در این دو گزاره، متغیرهای مدت تابش و انرژی، با متغیرهای زبانی مانند «طولانی»، «زیاد»، «کوتاه» و «کم» توصیف میشوند. در واقع، این دو گزاره منطقی در یک مدل ساده آنگستروم صدق میکنند.
مدلسازی تابش پراکنده
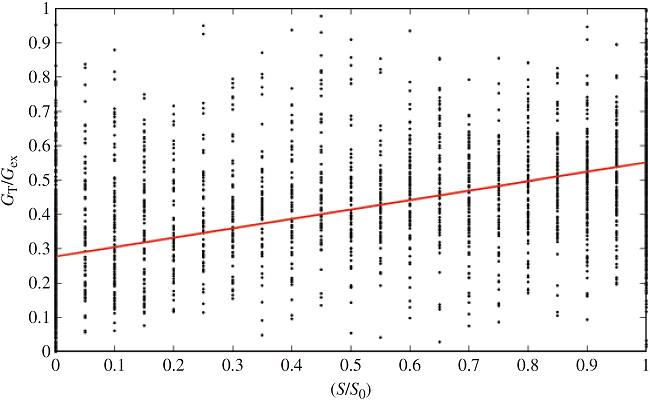
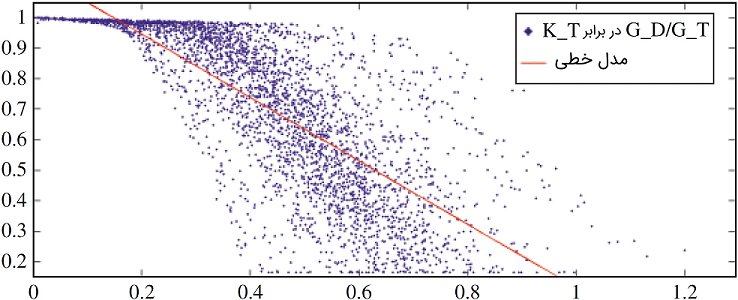
بسیاری از مدلهای خطی رابطه بین و شاخص شفافیت را توصیف کردهاند که برابر با است. معادله عمومی مدل خطی که انرژی خورشیدی پراکنده را محاسبه میکند میتوان به صورت زیر بیان کرد:
که در آن، و ضرایب مدل هستند.
میتوان رابطه مشابهی بین و شاخص شفافیت با مدل غیرخطی (۴۶) توصیف کرد:
مثال ۸
مثال ۷ را برای تابش پراکنده تکرار کنید.
حل: برنامه مربوط به این مثال به صورت زیر است:
پاسخ: شکل ۱۳
روشهای هوش مصنوعی برای مدلسازی تابش خورشیدی
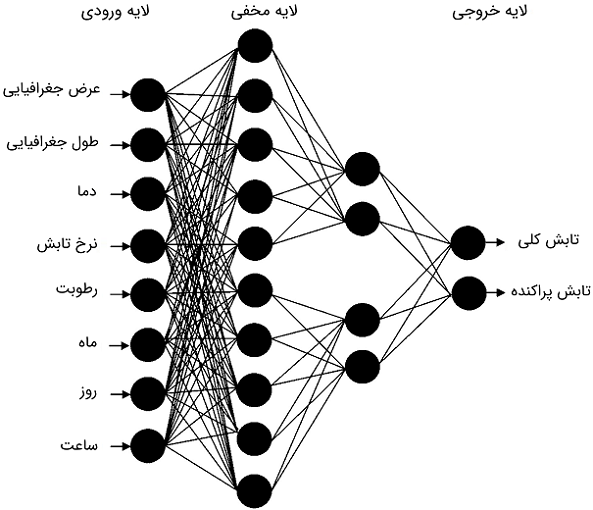
شبکههای عصبی مصنوعی (Artificial Neural Networks) یا ANN، سیستمهای پردازش اطلاعاتی غیرالگوریتمی و موازی هستند که رابطه بین ورودیها و خروجیها را با نمونههایی مانند دادههای ثبت شده قبلی یاد میگیرند. در این شبکهها، نرونها از طریق تعداد زیادی از پیوندهای وزندار که میتوانند سیگنالها را عبور دهند به هم وصل شدهاند. یک نرون، ورودیها را با اتصالات ورودی خود دریافت میکند، آنها را ترکیب میکند، در حالت کلی یک عملیات غیرخطی انجام میدهد و نتایج نهایی را به خروجی میبرد. در اینجا از برنامه متلب برای آموزش و تشکیل ANN برای مدلسازی انرژی کلی خورشید استفاده میکنیم. همچنین از یک «شبکه پیشخور پرسپترون چندلایه» (Feedforward Multilayer Perceptron Network) یا FFMLP استفاده شده است، زیرا رایجترین شبکه عصبی است که از نمونهها یاد میگیرد و برای این کار مناسب است. نمودار ساختار پایهای شبکه عصبی، در شکل ۱۴ نشان داده شده است. این شبکه سه لایه دارد: ورودی، مخفی و خروجی. هر لایه از طریق اتصالاتی با اندازه مختلف به نام وزن ارتباط دارد.
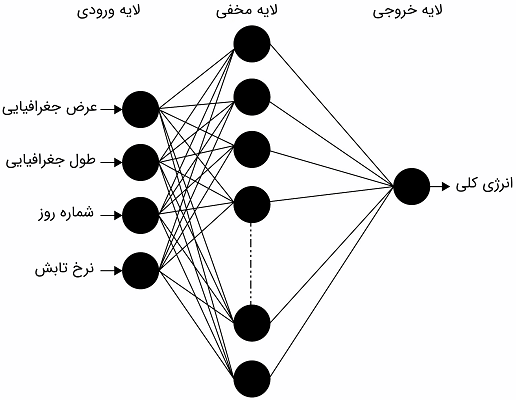
از چهار متغیر جغرافیایی و اقلیمی به عنوان ویژگیهای ورودی FFMLP استفاده میکنیم. این متغیرها عبارتند از شماره روز، طول جغرافیایی، عرض جغرافیایی و نسبت ساعت تابش روزانه (مدت تابش اندازهگیری شده در طول روز بر حداکثر مدت تابش ممکن روز). یک گره خروجی به عنوان پیشبینی شاخص شفافیت روزانه به عنوان خروجی در نظر گرفته شده است. تابع تبدیل نرونها یک تابع سیگموئید لگاریتمی است:
که در آن، مجموع وزندار ورودیها، سیگنال وارد شده به نرون اُم از لایه ورودی، وزن پیوند نرون به نرون در لایه مخفی و بایاس نرون اُم است.
شبکههای عصبی برای حل مسئله آموزش داده میشوند، نه اینکه برای انجام کاری برنامهریزی شوند. یادگیری از طریق آموزش حاصل میشود. به عبارت دیگر، آموزش، فرایندی است که در آن، شبکهها یاد میگیرند خطای بین مقدار خروجی و مقدار مرجع را به حداقل برسانند. در FFMLP، خطا با استفاده از الگوریتم آموزش اصطلاحاً پسانتشار، از لایه خروجی به لایه مخفی و سپس لایه ورودی به عقب منتشر میشود و با پسانتشار خطا، وزن پیوندهای بین نرونها بهروز میشود. در صورتی که تعداد نرونهای مخفی کافی باشد، با یک شبکه چندلایه میتوان هر تابع چندمتغیره پیوسته را با هر درجه دقت به صورت ریاضی تقریب زد. یک مشکل احتمالی که ممکن است رخ دهد، این است که شبکه به جای یادگیری و تعمیم ساختار اصلی دادهها، جزئیات غیرضروری موارد خاص آنها را یاد بگیرد.
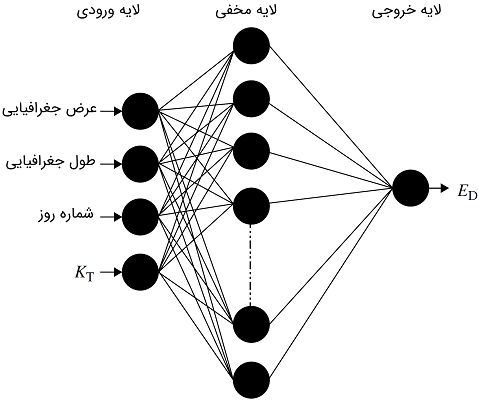
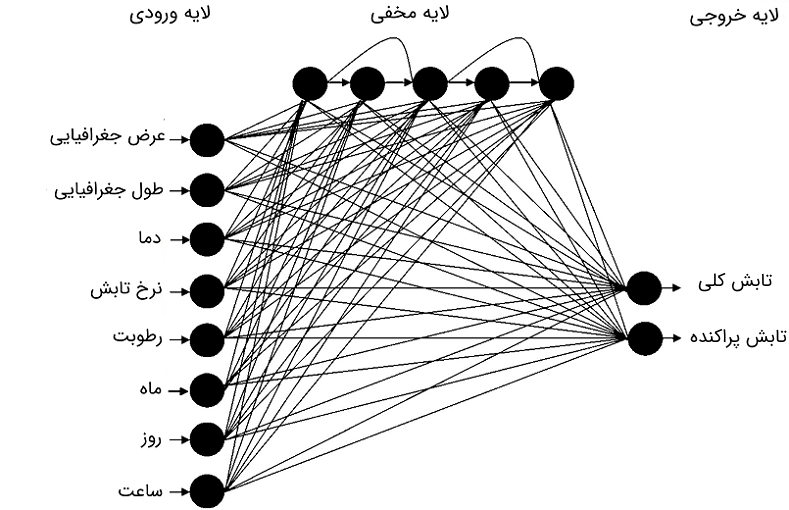
همان توپولوژی شبکه عصبی که در مدلسازی انرژی کلی مورد استفاده قرار گرفت، در مدلسازی انرژی خورشیدی پراکنده نیز استفاده میشود. شکل ۱۵، شبکه عصبی پیشبین انرژی پراکنده نشان میدهد. این شبکه، چهار ورودی شامل عرض جغرافیایی، طول جغرافیایی، شاخص شفافیت و شماره روز و یک متغیر خروجی دارد که انرژی پراکنده خورشیدی است. شکل ۱۶، این شبکه عصبی را نشان میدهد.
مثال ۹
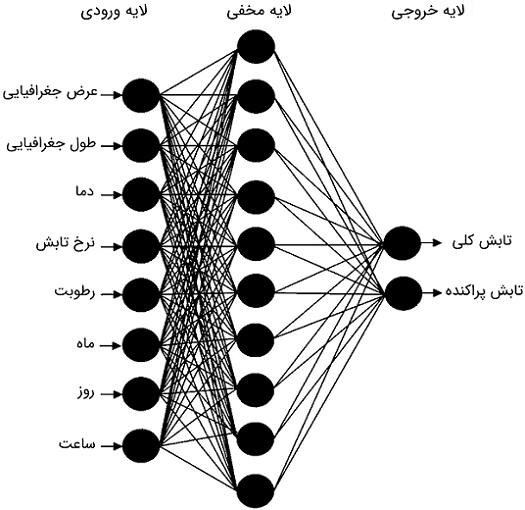
یک شبکه عصبی FFMLP ارائه دهید که تابش کلی ساعتی و تابش پراکنده را همانگونه که در شکل ۱۶ نشان داده شده پیشبینی کند.
حل: برنامه مربوط به این مثال به صورت زیر است:
پاسخ: شکل ۱۷
شبکه عصبی رگرسیون تعمیمیافته (Generalized Regression Neural Network) یا GRNN یک شبکه مبتنی بر احتمالات است. وقتی متغیر هدف قطعی باشد، این شبکه طبقهبندی انجام میدهد، در حالی که اگر متغیر هدف پیوسته باشد، امکان رگرسیون فراهم میکند. شکل ۱۸ نمودار GRNN را برای پیشبینی تابش ساعتی نشان میدهد.
شبکه شامل لایه ورودی، مخفی و خروجی است. لایه ورودی یک نرون برای هر متغیر پیشبینی کننده دارد. نرونهای ورودی طیف وسیعی از مقادیر را با تفریق از میانه و تقسیم بر دامنه میانچارکی، استاندارد میکنند. سپس نرونهای ورودی مقادیر هریک از نرونهای لایه مخفی را تغذیه میکنند. در لایه مخفی، برای هر مورد از مجموعه دادههای آموزش، یک نرون وجود دارد. نرون، مقادیر متغیرهای پیشبینی را برای هرمورد با مقدار هدف ذخیره میکند. هنگامی که این مقادیر با بردار ورودی به لایه ورودی اعمال میشود، یک نرون مخفی فاصله اقلیدسی نمونه آزمایش را از نقطه مرکز نرون محاسبه و سپس تابع هسته RBF را با استفاده از مقدار (مقادیر) سیگما اعمال میکند. مقدار حاصل به نرونها در لایه الگو منتقل میشود. لایه الگو (لایه جمعکننده) دو نرون دارد: یک واحد جمعکننده مخرج و یک واحد جمعکنندۀه صورت. واحد جمعکننده مخرج، وزنهای مقادیری را که از هریک از نرونهای مخفی میآید، جمع میکند. واحد جمعکننده صورت نیز وزن مقادیر ضرب شده در مقدار هدف واقعی را برای هر نرون مخفی جمع میکند. در نهایت، لایۀ تصمیم، مقدار موجود در واحد جمعکننده صورت را بر مقدار واحد جمعکننده مخرج تقسیم و از نتیجه به عنوان مقدار هدف پیشبینی شده استفاده میکند.
علاوه بر این همبستگی آبشاری، شبکههای عصبی شبکههایی «خودسازمانده» هستند. شبکه، تنها با نرونهای ورودی و خروجی شروع میشود. این پیکربندی، آبشاری نامیده میشود، زیرا خروجی هر نرون، ورودی نرون جدید را تغذیه میکند. با اضافه شدن نرونهای جدید به لایه مخفی، الگوریتم یادگیری تلاش میکند اندازه همبستگی بین خروجی نرون جدید و خطای باقیمانده شبکه را که باید حداقل شود، به حداکثر برساند. یک شبکه عصبی آبشاری سه لایه دارد: ورودی، مخفی و خروجی. لایه ورودی یک بردار از مقادیر متغیر پیشبین است. نرونهای ورودی، عملی جز توزیع مقادیر به نرونهای لایه مخفی و خروجی انجام نمیدهند. علاوه بر متغیرهای پیشبین، یک ورودی ثابت وجود دارد که بایاس نامیده میشود و هر یک از نرونهای مخفی و خروجی را تغذیه میکند. بایاس در یک وزن ضرب شده و به جمعکننده نرون اضافه میشود. در لایه مخفی، هر نرون ورودی در یک وزن ضرب و مقادیر وزنی حاصل با هم جمع میشوند تا یک مقدار ترکیبی تولید کنند. مجموع وزنی به یک تابع تبدیل وارد میشود و مقدار خروجی را نتیجه میدهد. خروجیهای لایه مخفی به لایه خروجی وارد میشود که مقادیری از همه نرونهای ورودی (از جمله بایاس) و تمام نرونهای لایه مخفی را دریافت کرده است. هر مقدار وارد شده به نرون خروجی در یک وزن ضرب و مقادیر وزنی حاصل دوباره برای تولید یک مقدار ترکیبی با هم جمع میشوند. مجموع وزنی به یک تابع تبدیل وارد میشود، سپس مقدار نهایی به دست میآید. شکل ۱۹ نمودار CFNN را برای پیشبینی تابش نشان میدهد.
مدلسازی ردیاب خورشید
اگر یک سیستم فتوولتائیک (PV) خورشید را دنبال کند، یعنی صفحات آن به سمت خورشید حرکت کند، تولید انرژی افزایش مییابد. در روزهایی با تابش مستقیم زیاد، میتوان با سازوکارهای ردیابی، انرژی نسبتاً بالایی را به دست آورد. در تابستان، افزایش بهره در روزهای صاف درصد و در زمستان درصد نسبت به سیستمهای PV با آرایش افقی ثابت است. بخش عمدهای از افزایش عملکرد حاصل از ردیابی را میتوان در تابستان به دست آورد. معمولاً افزایش بهره در زمستان که تعداد روزهای ابری بیشتری دارد، پایینتر است. به طور کلی، دو نوع دستگاه ردیابی وجود دارد: دومحوره و تکمحوره. سیستم دومحوره قابلیت بیشتری نسبت به سیستم تکمحوره دارد، زیرا میتواند روی نقطه بهینه متمرکز شود. با این حال، سیستم دومحوره از نظر فنی پیچیدهتر از سیستم تکمحوره است. در اروپای مرکزی، سیستمهایی که از محور دوگانه استفاده میکنند، عملکرد را تا درصد افزایش دادهاند. از سوی دیگر، عملکرد سیستم تکمحوره تقریباً درصد بیشتر از سیستمهای بدون ردیاب است.
شکل ۲۰ اصول حاکم بر ردیاب خورشیدی دومحوره را نشان میدهد. مسیر بین تصویر خورشید و کلکتور (صفحه خورشیدی)، استوا نامیده میشود. زاویه بین کلکتور و خط مرجع، زاویه شیب () و زاویه بین تصویر خورشید و کلکتور، زاویه فراز () نامیده میشود. زاویه () نیز زاویه بین تصویر خورشید و استوا است.

از منظر زمین، خورشید درطول روز در سراسر آسمان در حال حرکت است. در مورد کلکتورهای خورشیدی ثابت، تصویر ناحیه کلکتور در صفحهای که عمود بر جهت تابش است، به وسیله تابع کسینوسی از زاویه تابش داده میشود. زاویه تابش () بزرگتر، به معنی توان پایینتر است.
همانطور که در شکل ۲۰ نشان داده شده است، حداکثر توان را میتوان در زاویه شیبی به دست آورد که زاویه تابش صفر باشد. روابط بین زاویههای شیب، فراز و تابش به صورت زیر است:
قبل از ظهر:
و بعد از ظهر:
برای جذب حداکثر تابش توسط کلکتور، زاویه تابش () باید صفر باشد، بنابراین زاویه شیب بهینه را میتوان به صورت زیر تعیین کرد:
نمودار شماتیک یک ردیاب خورشیدی در شکل ۲۱ نشان داده شده است. این ردیاب شامل دو بخش است: یک موتور پلهای که توسط یک میکروکنترلر و یک جعبهدنده هدایت میشود تا گشتاور موتور را برای هدایت کلکتور افزایش دهد.
فناوریهای موتور پلهای و میکروکنترلر را میتوان برای تشکیل یک کنترلکننده دقیق ترکیب کرد تا شیب کلکتور خورشیدی تا حد ممکن به زاویه خورشید نزدیک شود.
مثال ۱۰
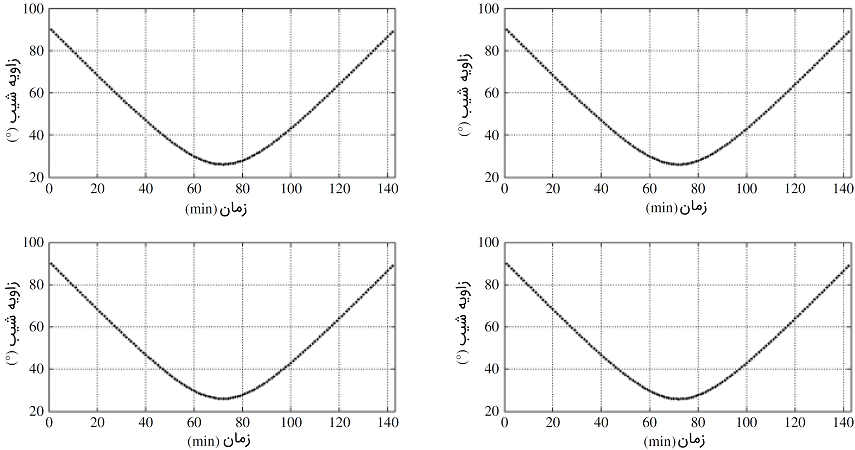
مدل یک ردیاب خورشیدی تکمحوره را در متلب بنویسید که هر 5 دقیقه، خورشید را ردیابی کند.
حل: کد متلب این مثال به صورت زیر است:
پاسخ: شکل ۲۱













باسلام واحترام ضمن تبریک سال نو و تشکر از ارایه مطالب مفیدتون ، لطفا درصورت امکان برای بازتولید مقاله انرژی خورشیدی راهنمایی کنید. باسپاس
باسلام وخسته نباشیدعالی بوداستاد،من اصلامتلب بلدنیستم منبعی هست که ساده اموزش متلب اموزش بده
سلام احمد عزیز.
از اینکه این آموزش برایتان مفید بوده است، بسیار خوشحالیم.
در آموزش «برنامه نویسی در متلب (MATLAB) — راهنمای گام به گام (+ دانلود فیلم آموزش رایگان)» به زبان ساده و گام به گام برنامهنویسی در متلب را شرح دادهایم.
شاد و پیروز باشید.
با درود ارج به دانش و زکات علم آموزی حضرتعالی
بسیار آموزنده است.
سلام احسان عزیز.
از اینکه این آموزش برایتان مفید بوده، بسیار خوشحالیم.
شاد و پیروز باشید.
سلام
با تشکر از مطالب ارزنده شما.
چگوه میتوان زاویه Azimuth رو هم در نظر گرفت؟
ممنون
عباس