قضیه کانتور در نظریه مجموعه | به زبان ساده
در ریاضیات و بخصوص در نظریه اعداد، قضیه کانتور اهمیت ویژهای دارد. در نوشتارهای دیگر فرادرس در مورد عدد اصلی یک مجموعه صحبت کردیم. در آنجا دیدیم که تعداد اعضای یک مجموعه متناهی توسط عدد اصلی آن مشخص میشود. ولی زمانی که با یک مجموعه نامتناهی (شمارا یا ناشمارا) مواجه هستیم، شمارش تعداد اعضای مجموعه امکانپذیر نیست و به سادگی نمیتوان عدد اصلی یک مجموعه را مشخص کرد. قضیه کانتور در نظریه مجموعه دقیقا به همین موضوع اشاره دارد و ابزاری برای مرتبسازی مجموعهها براساس عدد اصلی آنها ارائه میدهد و نشان میدهد که چه رابطهای بین عدد اصلی یک مجموعه با عدد اصلی مجموعه توانی آن برقرار است.


برای آشنایی بیشتر با نظریه مجموعهها (Set Theory) و اصطلاحات به کار رفته در این متن، پیشنهاد میشود نوشتارهای اصل خوش ترتیبی در نظریه اعداد — به زبان ساده و نظریه اعداد و کاربردهای آن — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب مجموعه متناهی و نامتناهی — به زبان ساده و اعداد طبیعی — به زبان ساده نیز خالی از لطف نیست. به این ترتیب آمادگی لازم برای درک بهتر این متن را پیدا خواهید کرد.
قضیه کانتور در نظریه مجموعه
یکی از قضیههای اصلی و پایه در نظریه مجموعه (Set Theory)، «قضیه کانتور» (Cantor's Theorem) است. براساس این قضیه مشخص میشود که «عدد اصلی» (Cardinality) برای «مجموعه توانی» (Power Set) هر مجموعه (مثل ) از عدد اصلی مجموعه ، به طور اکید بزرگتر است. در این نابرابری، بخصوص روی بزرگتر و علامت اکید، اصرار وجود دارد.
این قضیه را «گئورگ کانتور» (Georg Cantor) یا به قولی «جورج کانتور»، در مقالهای در سال ۱۸۹۱ منتشر و اثبات کرد. او در این مقاله نشان داد که اگر یک تابع روی باشد بطوری که مقادیر مثلا صفر و یک را بگیرید (درست مانند تابع نشانگر)، آنگاه تابع در برد تابع قرار نخواهد داشت. این قضیه و اثبات آن را در ادامه متن مورد بررسی دقیقتر قرار خواهیم داد. همچنین به خصوصیات و ویژگیهای مربوط به تناقضهای مطرح شده در قضیه و هم اثبات آن نیز، در این متن، اشارههایی خواهیم کرد.
سالها بعد از کانتور، «فدریک زرملو» (Ernst Friedrich Ferdinand Zermelo) طی مقالهای با عنوان «مطالعاتی روی مبانی نظریه مجموعه» به قضیهای میپردازد که آن را «قضیه کانتور» نامگذاری کرده و براساس آن، مبانی اولیه نظریه مجموعه را در سال ۱۹۰۸ منتشر کرد. او قضیه، مجموعه و تابع کانتور را بهشت ریاضیات و نظریه مجموعهها نام نهاد.

نمایش یا اثبات قضیه کانتور برای مجموعههای متناهی به سادگی با مشخص کردن عدد اصلی مجموعه و مجموعه توانی آن، صورت میگیرد. کافی است عمل شمارش اعضای هر یک از این مجموعهها را انجام دهیم. با توجه به اینکه مجموعه تهی نیز زیرمجموعه هر مجموعه محسوب میشود، عدد اصلی مجموعه توانی یک مجموعه مثل (با عدد اصلی ) برابر است با . واضح است که برای هر مقدار نامنفی رابطه زیر برقرار است.
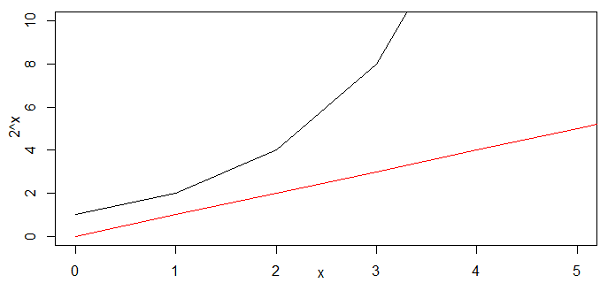
نکته: این موضوع را به کمک استقرا میتوان اثبات کرد. البته نگاهی به تابع و مقایسه آن با نیز روشی دیگر برای نمایش این موضوع است. این کار در تصویر زیر صورت گرفته است. واضح است که برای مقادیر بزرگتر از صفر، همیشه منحنی که با رنگ سیاه مشخص شده از بزرگتر است.
اهمیت قضیه کانتور در این بین، نمایش این رابطه برای مجموعههای نامتناهی (شمارشپذیر یا ناشمارا) است. او توانست نشان دهد که برای مجموعه نامتناهی ولی شمارشپذیر اعداد طبیعی با عدد اصلی و مجموعه توانی اعداد طبیعی با عدد اصلی ، رابطه زیر برقرار است.
این موضوع نشان میدهد که عدد اصلی مجموعه توانی اعداد طبیعی با عدد اصلی اعداد حقیقی برابر بوده، در نتیجه مجموعه توانی اعداد طبیعی ناشمارا است. به بیان دیگر اگر مجموعه توانی اعداد طبیعی باشد، خواهیم داشت:
بوسیله قضیه کانتور میتوان یک رابطه ترتیبی بین اعداد کاردینال ایجاد کرد بطوری که طبق یک «رابطه سلسله مراتبی بیپایان» (Endless Hierarchy of Infinite Cardinals)، هر مجموعه دارای عدد اصلی بزرگتر از مجموعه قبلی باشد. همچنین این قضیه بیان میکرد که بزرگترین عدد اصلی یا کاردینال وجود ندارد، همانطور که بزرگترین بینهایت نیز وجود ندارد.
صورت قضیه کانتور
فرض کنید تابع یک نگاشت از مجموعه به مجموعه توانی (Power Set) باشد. آنگاه این تابع، پوشا (Surjective) نخواهد بود. به این معنی که یک تناظر یک به یک از مجموعه با برقرار نخواهد شد. به عنوان نتیجه میتوان گفت که برای هر مجموعهای مثل برقرار است.
اثبات قضیه کانتور
اثبات این قضیه با توجه به تعریف پوشا بودن تابع مشخص میشود. فرض کنید مجموعه به صورت اعضای از مجموعه تعریف شود که به برد تابع تعلق نداشته باشند.
با فرض پوشا بودن تابع باید وجود داشته باشد که . اما با توجه به ساختار مجموعه خواهیم داشت:
که این تناقض ایجاد کرده در نتیجه تابع نمیتواند پوشا باشد. از طرفی فرض کنید که تابع یک نگاشت یک به یک (Injective) از به به صورت زیر باشد.
به این ترتیب باید داشته باشیم:
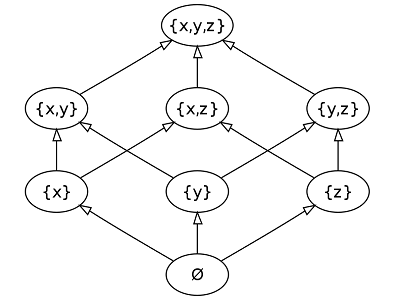
در تصویر زیر یک رابطه سلسله مراتبی برای مجموعهای براساس سه عضو () ایجاد شده است. هر سطر از این رابطه سلسله مراتبی، زیرمجموعههایی از مجموعه اصلی را مشخص کرده است که براساس تعداد اعضایشان در یک سطر دیده میشوند. برای مثال در سطر اول از پایین، مجموعه تهی (با عدد اصلی صفر) قرار گرفته و در سطر دوم نیز زیرمجموعههای تک عضوی با عدد اصلی برابر با ۱ دیده میشوند. همچنین زیرمجموعههایی دو عضوی و سه عضوی نیز در بالای این نمودار قرار میگیرند. مشخص است که اگر نمودار را از پایین به بالا، در نظر بگیریم، عدد اصلی سطرها به صورت افزایشی بوده و مقدار هر سطر از سطر زیرین بیشتر است. در نهایت نیز عدد اصلی مجموعه اصلی، قرار گرفته است.
توضیحاتی در مورد اثبات قضیه کانتور
براساس تعریف عدد اصلی، اگر یک تابع یک به یک (و نه معکوس پذیر) بین دو مجموعه و وجود داشته باشد، آنگاه است و برعکس. به این ترتیب کافی است نشان دهیم تابعی پوشا بین این دو مجموعه نمیتوان با شرایط گفته شده، پیدا کرد.
به این ترتیب اثبات با این هدف انجام میشود که هیچ نگاشتی از عناصر به زیرمجموعههای وجود ندارد که به صورت تابع بیان شود. پس کافی است نشان دهید که یک زیرمجموعه از (مثل ) وجود دارد که تحت تابع برای هر با برابر نیست.
نکته: در اینجا فرض کنید تابع هر یک از زیرمجموعههای را میسازد. این ساختار به «مجموعه قطری کانتور تابع » یا (Cantor diagonal set of f) نیز مشهور است.

به این ترتیب برای هر ، میتوان در نظر گرفت به شرطی که و برعکس. برای هر ، مجموعههای و نمیتوانند برابر باشند، زیرا براساس عناصر از تشکیل شده که تصویر آنها (تحت تابع ) با مقدار خودشان برابر نیست.
از طرفی میتوان را به شکلی در نظر گرفت که یا یا خارج از آن است (). در حالت اول، نمیتواند برابر با باشد زیرا بوده و براساس ساختار مجموعه داریم، . در حالت دوم نیز برابر با نیست، زیرا براساس فرض است و براساس ساختار مجموعه خواهیم داشت .
به این ترتیب با استفاده از «برهان خلف» (reductio ad absurdum)، فرض اولیه باید نادرست باشد. به علاوه هیچ وجود ندارد که . به بیان دیگر ، تصویر نیست و نگاشتی از عناصر مجموعه توانی نخواهد بود. در نتیجه یک تابع پوشا نیست.
در نهایت برای اتمام قضیه، باید یک تابع یک به یک از به مجموعه توانی معرفی کنیم. چنین تابعی میتواند به صورت نگاشتی از به یعنی مجموعه تک عضوی از باشد.
قضیه کانتور برای مجموعههای نامتناهی شمارشپذیر
این بار میخواهیم به واسطه یک مجموعه نامتناهی ولی شمارشپذیر، اثبات را مورد بررسی قرار دهیم. بدون آنکه کلیت اثبات لطمهای بخورد، فرض کنید که مجموعه ، همان مجموعه اعداد طبیعی باشد.
همچنین در نظر بگیرید که این مجموعه با مجموعه توانی خود یعنی همشمارا (Equinumerous) باشد. بهتر است ابتدا نگاهی به این مجموعه توانی بیاندازیم.
مشخص است که مجموعه توانی شامل بینهایت زیرمجموعه از است. به این ترتیب نمایشی از اعضای مجموعه توانی اعداد طبیعی حاصل میشود. حال سعی میکنیم بتوانیم یک تناظر بین مجموعه توانی و اعداد طبیعی پیدا کنیم. این کار باید به شکلی صورت گیرد که هیچ یک از اعضای مجموعه توانی بدون عضوی مرتبط از مجموعه اعداد طبیعی باقی نماند. برای مثال ممکن است این تناظر به صورت زیر برقرار شده باشد.
اینطور به نظر میرسد که در بعضی از اعضای این نگاشت، یک عدد طبیعی با مجموعهای که شامل آن عدد است مرتبط شده است. مثلا با مجموعه ارتباط دارد. برای تنوع به این اعداد در تناظر یاد شده، «اعداد خودخواه» (Selfish Numbers) یا اعداد خودبین، میگوییم. به این ترتیب عدد ۲ در رابطه ذکر شده، یک عدد خودخواه است زیرا با عضوی از مجموعه توانی در تناظر است که شامل عدد میباشد. در عوض عدد ۱ یا ۳، خودخواه نیستند زیرا در تناظر با مجموعهای هستند که شامل این اعداد نیست. این اعداد را هم «غیرخودخواه» (non-selfish) یا ایثارگر مینامیم.
براساس این ایده برای تقسیم اعداد طبیعی در تناظر، تناقضی که به دنبالش بودیم را ایجاد خواهیم کرد. فرض کنید مجموعهای از همه اعداد ایثارگر در اعداد طبیعی است. براساس تعریف مجموعه توانی، شامل همه مجموعههای حاصل از اعداد طبیعی است بخصوص نیز یکی از اعضای مجموعه توانی خواهد بود.
اگر نگاشت یا تناظر یاد شده، پوشا (surjective) باشد، مجموعه باید شامل یک مقدار باشد که دارای تناظر با یک عضو از مجموعه اعداد طبیعی مثلا باشد. البته این امر مشکلساز است. اگر در بوده و یک عدد خودخواه باشد، با تعریف مجموعه دچار تناقض میشود. اگر در نباشد، آنگاه یک عدد ایثارگر است و باید عضوی از مجموعه باشد. در نتیجه هیچ عنصری مانند وجود ندارد که حاصل نگاشت از باشد.
توجه داشته باشید که هیچ عدد طبیعی وجود ندارد که بتواند با تشکیل یک زوج در تناظر بدهد. این موضوع همان فرض وجود تناظر پوشا بین اعداد طبیعی و مجموعه توانی آن را لغو میکند.
به این امر هم توجه کنید که ممکن است مجموعه ، تهی باشد که به معنی آن است که هر عدد طبیعی به یک زیرمجموعه از اعدادی طبیعی شامل نگاشت میشود. یعنی همه اعداد به یک مجموعه ناتهی نگاشت شده و هیچ عددی با مجموعه تهی، نگاشت نمیشود. از طرفی مجموعه تهی، یک زیرمجموعه از مجموعه اصلی است و در مجموعه توانی حضور دارد. در نتیجه باز هم نگاشت معرفی شده نمیتواند تمام مجموعه توانی را بپوشاند.
در روند اثبات این قضیه، اثبات کردیم که عدد اصلی مجموعه اعداد طبیعی هرگز با عدد اصلی مجموعه توانی آن برابر نیست. همچنین از قبل میدانستیم که عدد اصلی مجموعه توانی هیچگاه از عدد اصلی خود مجموعه کوچکتر نیست، زیرا مجموعه توانی شامل مجموعههای تک عضوی از مجموعه اصلی نیز هست. در نهایت تنها حالتی که برای نمایش رابطه بین اعداد اصلی این دو مجموعه باقی میماند، بزرگتر بودن اکید عدد اصلی مجموعه توانی از عدد اصلی مجموعه اعداد طبیعی است.
از آنجایی که بین هر مجموعه نامتناهی شمارا و اعداد طبیعی، یک تناظر یک به یک وجود دارد، قضیه یاد شده برای هر مجموعه نامتناهی شمارا، به همین شیوه قابل اثبات است.
تناقضهای مرتبط با قضیه کانتور
قضیه کانتور و اثبات آن، رابطه بسیار نزدیکی با دو تناقض در نظریه مجموعه دارد. ابتدا به تناقض کانتور اشاره میکنیم که به همراه قضیه کانتور به بررسی «مجموعه جهانی» (Universal Set) یا مجموعه مرجع () میپردازد.
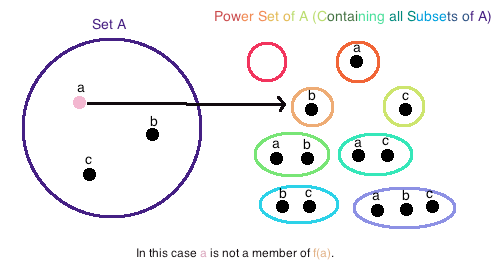
قضیه کانتور بیان میداد که تعداد اعضای یا عدد اصلی مجموعه توانی از عدد اصلی خود مجموعه ، بزرگتر است.
از طرفی همه عناصر مجموعه توانی ، مجموعه محسوب میشوند که البته یکی از اعضای نیز خواهد بود. در نتیجه:
که امری متناقض به نظر میرسد.
تناقض بعدی از اثبات کانتور استخراج میشود. فرض کنید تابع که برای اثبات قضیه کانتور به کار رفت، «تابع همانی» (Identity Function) باشد. در این صورت عناصر قطری مجموعه کانتور، به مجموعه راسل (Russell Set) برای مجموعه تبدیل میشوند.
اثبات قضیه کانتور با در نظر گرفتن اینکه مجموعه مرجع یا مجموعه همه مجموعهها () وجود دارد صورت گرفته و در نتیجه برای مجموعه منجر به تناقض میشود.
به این تناقض، «پارادوکس راسل» (Russell's Paradox) نیز گفته میشود.
خلاصه و جمعبندی
قضیه کانتور راه را برای بسیار از نظریههای دیگر در حوزه ریاضیات و مجموعهها باز کرد. به همین علت نیز در این نوشتار به این قضیه پرداخته و جوانب مختلف آن را مورد بررسی قرار دادیم. واضح است که تصور مجموعههایی که نامتناهی عضو داشته باشند، به راحتی میسر نیست ولی ذهن خلاق ریاضیدان و دانشمند بزرگ آلمانی-روسی «گئورگ کانتور» یا به قولی «جورج کانتور» توانست این محدودیتها را کنار زده و پنجرهای به سوی بینهایت باز کند.













در متن تابع پوشا bijective نوشته شده، پوشا surjective ,
bijective دوسویی هست
با سلام،
متن بازبینی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس
سلام وقت بخیر امکانش هست درباره پاردوکس راسل بیشتر و کمی ساده تر توضیح بدید. تعاریفی که اومده خیلی انتزاعی هستن و فهمشون برای من کمی مشکله