قضیه منلائوس — به زبان ساده
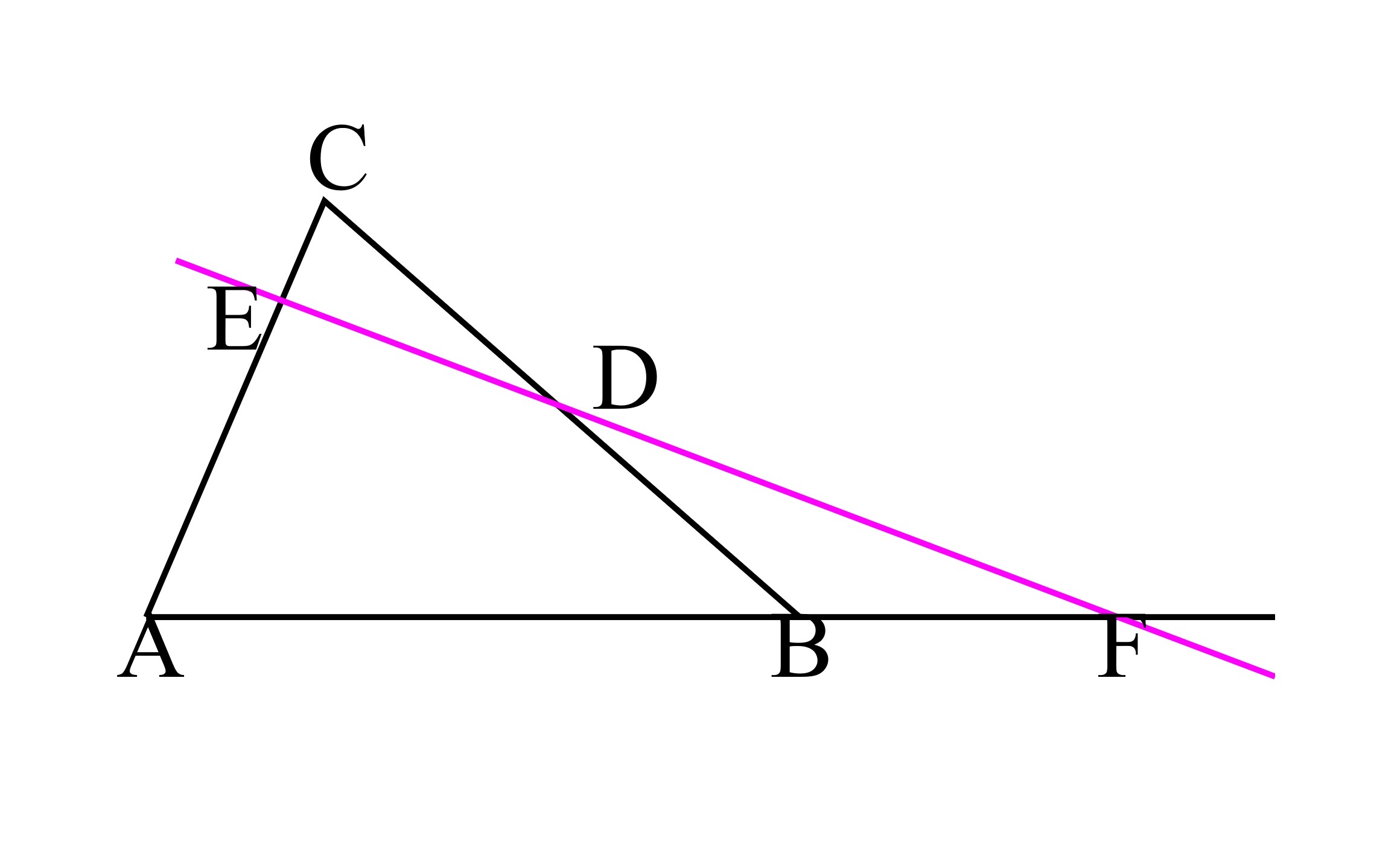
«قضیه منلائوس» (Menelaus' Theorem) درباره نسبتهای به دست آمده از خط قطع کننده اضلاع یک مثلث است. عکس این قضیه (یعنی سه نقطه روی یک مثلث همخط هستند اگر و تنها اگر در یک معیار مشخص صدق کنند) نیز صحیح است و در اثبات همخط بودن سه نقطه کاربرد دارد.
«قضیه سوا» (Ceva's Theorem) اساساً همتای این قضیه است و میتوان از آن برای اثبات همرس بودن سه خط در یک نقطه استفاده کرد. دو قضیه ساختار مشابهی داشته و کاربرد فراوانی در طیف گستردهای از انواع مسائل هندسه دارند.
قضیه منلائوس
قضیه منلائوس: قضیه منلائوس بیان میکند که اگر خطی مثلث $$ \triangle ABC $$ یا امتداد اضلاع آن را قطع کند، در نقاط $$ D $$، $$ E $$ و $$ F $$، رابطه زیر برای آن صادق است:
$$ \large \frac { A D } { D B } \times \frac { B E }{ E C } \times \frac { C F } { F A } = 1 . $$
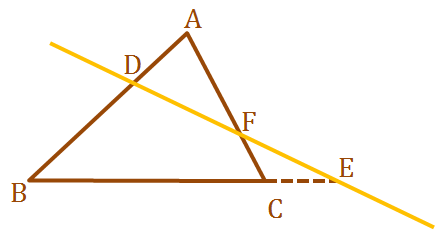
عکس قضیه منلائوس: فرض کنید سه نقطه $$ D $$، $$ E $$ و $$ F $$ به ترتیب روی اضلاع (یا امتداد) $$ A B $$، $$ BC $$ و $$ AC $$ باشند، به گونهای که یک یا سه تا از آنها در امتداد اضلاع قرار گیرند. در نتیجه، نقاط $$ D $$، $$ E $$ و $$ F $$ همخط هستند اگر و تنها اگر
$$ \large \frac { A D } { D B } \times \frac { B E }{ E C } \times \frac { C F } { F A } = 1 . $$
عکس قضیه در اثبات همخط بودن نقاط بسیار کارآمد است.
اثبات: خطوط $$ AA'$$، $$ BB'$$ و $$ CC'$$ را رسم میکنیم که عمود بر خط زرد هستند.
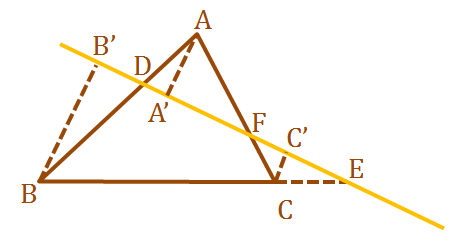
حال از آنجا که $$ \triangle A A' D \sim \triangle B B' D $$، داریم:
$$ \large \frac { A D } { D B } = \frac { A A' } { B B' } . $$
با توجه به $$ \triangle A A' F \sim \triangle C C' F $$، میتوان نوشت:
$$ \large \frac { C F } { F A } = \frac { C C' } { A A' } . $$
بنابراین:
$$ \large \frac { A D } { D B } \times \frac { B E }{ E C } \times \frac { C F } { F A } = \frac { A A' } { B B' } \times \frac { B B' }{ C C' } \times \frac { C C' } { A A' } = 1 .\ _ \square $$
نکات زیر قابل توجه است:
- حتی اگر خط زرد با مثلث تقاطع نداشته باشد، این تساوی برقرار است (این یعنی خط زرد امتداد اضلاع مثلث را قطع میکند).
- اگر خط زرد یکی از رئوس مثلث را قطع کند، آنگاه یک $$ 0 $$ در مخرج معادله ظاهر میشود که تعریف نشده است. برای حل این مشکل، میتوان قضیه منلائوس را به صورت $$ A D \times B E \times C F = D B \times E C \times F A . $$ بازنویسی کرد.
مثالی از قضیه منلائوس
از رأس $$ C $$ زاویه قائمه مثلث $$ \triangle A B C $$، ارتفاع $$ CK $$ و همچنین نیمساز $$ C E $$ مثلث $$ \triangle ACK $$ رسم شدهاند. خط گذرنده از نقطه $$ B $$ موازی $$ C E $$ با $$ C K $$ در نقطه $$ F $$ برخورد میکند. ثابت کنید خط $$ E F $$ پاره خط $$ A C $$ را به دو نیم تقسیم میکند.
حل: از آنجا که $$ \angle B C E = 9 0 ° - \frac { \angle B } { 2 } $$، داریم: $$ \angle B C E = \angle B E C $$ و در نتیجه، $$ B E = B C $$. بنابراین:
$$ \large C F : K F = B E : B K = B C : B K , \quad A E : K E = C A : C K = B C : B K . $$
فرض کنید $$ E F $$ خط $$ A C $$ را در نقطه $$ D $$ قطع کند. طبق قضیه منلائوس، $$ \frac { A D } { C D } \cdot \frac { C F } { K F } \cdot \frac { K E } { A E } = 1 $$. با توجه به این واقعیت که $$ C F : K F = A E : K E $$، به اثبات مورد نظر میرسیم.
کاربرد قضیه منلائوس
از عکس قضیه منلائوس برای اثبات قضیه لاپلاس استفاده میکنیم. مجدداً عکس قضیه منلائوس را بیان میکنیم.
معکوس قضیه منلائوس: فرض کنید سه نقطه $$ D $$، $$ E $$ و $$ F $$ روی اضلاع (یا امتداد اضلاع) به ترتیب $$ A B $$، $$ BC $$ و $$ A C $$ قرار دارند به گونهای که یک یا سه تا از آنها در امتدار اضلاع باشد. آنگاه نقاط $$ D $$، $$ E $$ و $$ F $$ همخط هستند اگر و تنها اگر
$$ \large \frac { A D } { D B } \times \frac { B E } { E C } \times \frac { C F } { F A } = 1 . $$
از این رابطه میتوان برای اثبات قضیه پاسکال استفاده کرد، که بیان میکند:
قضیه لاپلاس: شش نقطه روی یک دایره محیطی به نامهای $$ A $$، $$ C $$، $$ E $$، $$ B $$، $$ F $$ و $$ D $$ داریم (که میتوانند منطق بر هم نیز باشند) و تقاطعهای $$ A B $$ و $$ D E $$، $$ A F $$ و $$ C D $$، و $$ B C $$ و $$ E F $$ همخط هستند.
اثبات: فرض کنید $$ G $$ تقاطع $$ \overline{CD} $$ و $$ \overline {FA}$$ بوده و $$ H $$ تقاطع $$ \overline {AB} $$ و $$ \overline{DE}$$ و همچنین، $$I$$ تقاطع $$ \overline { BC} $$ و $$ \overline {EF} $$ باشند. اثبات خواهیم کرد که این سه نقطه همخط هستند (روی یک خط قرار دارند).
فرض کنید $$ U $$ تقاطع $$ \overline { CD} $$ و $$ \overline { EF} $$ بوده و $$ V $$ تقاطع $$ \overline { AB} $$ و $$ \overline { EF} $$ و همچنین، $$ W $$ تقاطع $$ \overline { AB} $$ و $$ \overline { CD} $$ باشد. طبق قضیه منلائوس در مثلث $$ \triangle U V W $$ و خط $$ HDE $$، داریم:
$$ \large \dfrac { V H } { W H } \cdot \dfrac { W D } { U D } \cdot \dfrac { U E } { V E } = 1 . $$
همچنین، طبق قضیه منلائوس در مثلث $$ \triangle U V W $$ و خط $$ AGF $$، میتوان نوشت:
$$ \large \dfrac { V A } { W A } \cdot \dfrac { W G } { U G } \cdot \dfrac { U F } { V F } = 1 . $$
بار دیگر، طبق قضیه منلائوس در مثلث $$ \triangle U V W $$ و خط $$ BCI $$، خواهیم داشت:
$$ \large \dfrac { V B } { W B } \cdot \dfrac { W C } { U C } \cdot \dfrac { U I } { V I } = 1 . $$
با ضرب این سه تساوی در یکدیگر، داریم:
$$ \large \dfrac { V H } { W H } \cdot \dfrac { W D } { U D } \cdot \dfrac { U E } { V E } \cdot \dfrac { V A } { W A } \cdot \dfrac { W G } { U G } \cdot \dfrac { U F } { V F } \cdot \dfrac { V B } { W B } \cdot \dfrac { W C } { U C } \cdot \dfrac { U I } { V I } = 1 . $$
با بازآرایی عبارت بالا، میتوان نوشت:
$$ \large \dfrac { W D } { U D } \cdot \dfrac { U E } { V E } \cdot \dfrac { V A } { W A } \cdot \dfrac { U F } { V F } \cdot \dfrac { V B } { W B } \cdot \dfrac { W C } { U C } \cdot \dfrac { V H } { W H } \cdot \dfrac { W G } { U G } \cdot \dfrac { U I } { V I } = 1 . $$
طبق «قوت یک نقطه» (Power of a Point)، خواهیم داشت:
$$ \large \begin {aligned} \dfrac { W D } { U D } \cdot \dfrac { U E } { V E } \cdot \dfrac { V A } { W A } \cdot \dfrac { U F } { V F } \cdot \dfrac { V B } { W B } \cdot \dfrac { W C } { U C } & = \dfrac { W D \times W C } { W A \times W B } \cdot \dfrac { V A \times V B } { V E \times V F } \cdot \dfrac { U E \times U F } { U C \times U D } \\\\ & = 1 . \end {aligned} $$
بنابراین، ضربهای بالا به شکل زیر ساده میشود:
$$ \large \dfrac { V H } { W H } \cdot \dfrac { W G } { U G } \cdot \dfrac { U I } { V I } = 1 $$
در نهایت، طبق قضیه منلائوس، $$ G $$، $$ H $$ و $$ I $$ همخط هستند.










