فیلتر کالمن در متلب — راهنمای کاربردی

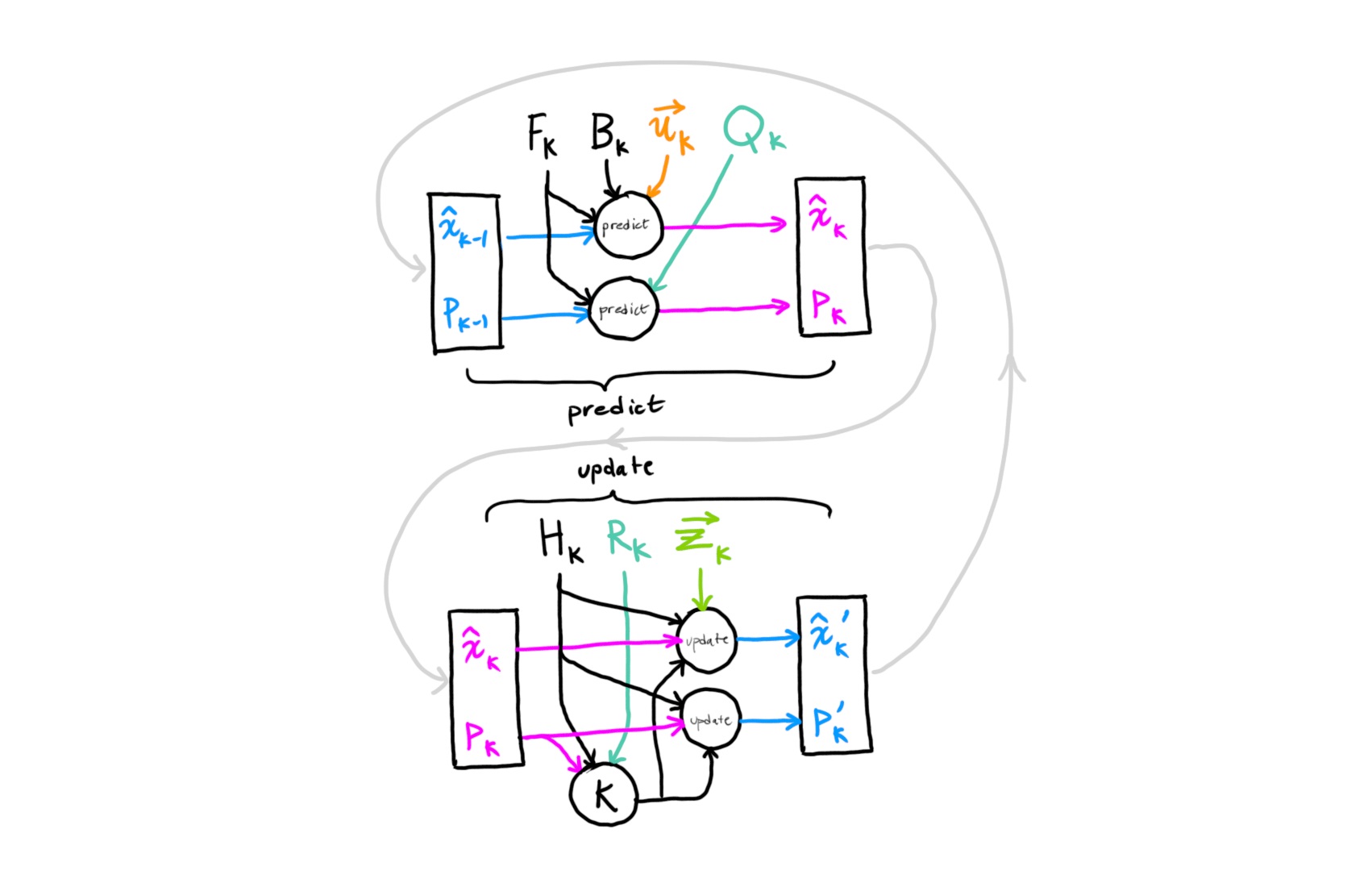
در آموزش‌های قبلی مجله فرادرس با فیلتر کالمن آشنا شدیم. فیلتر کالمن معادل مشاهده‌گر برای رگولاتورهای مرتبه دوم خطی است و به همین دلیل تخمین‌گر مرتبه دوم خطی نیز نامیده می‌شود. در این آموزش، ضمن بیان مختصر مفاهیم، با پیاده‌سازی فیلتر کالمن در متلب آشنا خواهیم شد.

فیلتر کالمن گسسته

از آنجایی که تخمین با استفاده از فیلتر کالمن با اندازه‌گیری و انتشار حالت گره خورده است، درک پیاده‌سازی گسسته آن‌ ساده‌تر است. سیستم زیر را در نظر بگیرید:

$$ \large X _ { k + 1 } = A X _ { k } + B u _ { k } + F w _ { k } $$

فیلم آموزش کنترل مدرن – حل ۱۰۰ مساله در فرادرس

کلیک کنید

که در آن، $$w _ k $$ نامعینی دینامیک سیستم است که به عنوان یک فرایند گاوسی با کوواریانس $$ E(w_k w_k^T ) = Q $$ نمایش داده شده است. متغیرهای حالت $$ X_k $$ نیز با فرایندهای دو به دو گوسی مستقل با کوواریانس $$ P _ k$$ مدل می‌شوند. شرایط اولیه نیز حالت $$ X(0) = X_0 $$ و کوواریانس $$P_0 $$ هستند.

اندازه‌گیری به صورت زیر تقریب زده شده است:

$$ \large Y _ k = C X _ k + D u _ k + v _ k $$

که در آن، $$v _ k $$ نامعینی در اندازه‌گیری با کواریانس $$ E(v_k v_k^T ) = R $$ است.

۱. انتشار حالت

دینامیک سیستم به صورت زیر بیان می‌شود:

$$ \large X _ { k + 1 } = A X _ { k } + B u _ { k } + F w _ { k } $$

برای جداسازی تخمین‌های حالت قبل و بعد از اندازه‌گیری، موارد زیر را تعریف می‌کنیم:

• $$ X _ {k|k}$$ به عنوان تخمین بعد از اندازه‌گیری در گام $$k$$
• $$ X _ { k + 1 |k} $$ به عنوان تخمین حالت بعد از دنبال کردن دینامیک سیستم

بنابراین، مقدار بعدی قابل انتظار حالت به صورت زیر خواهد بود:

$$ \large E ( X _ { k + 1 | k } ) = A E ( X _ { k | k } ) + B E ( u _ k ) + E ( F w _ k ) $$

$$ \large \hat { X } _ { k + 1 | k } = A \hat { X } _ {k | k } + B u _ k $$

خطای بین تخمین حالت و امید ریاضی، قبل از اندازه‌گیری به صورت زیر نمایش داده می‌شود:

$$ \large X _ { k + 1 | k } - \hat { X } _ { k + 1 | k } = A X _ { k | k } + B u _ k + F w _ k - ( A \bar { X } _ { k | k } + B u _ k ) $$

$$ \large e _ { k + 1 | k } = X _ { k + 1 | k } - \bar { X } _ { k + 1 | k } = A e _ { k | k } + F w _ k $$

بنابراین، کوواریانس حالت قبل از اندازه‌گیری برابر خواهد بود با:

$$ \large P _ { k + 1 | k } = E ( e _ { k + 1 | k } e _ { k + 1 | k } ^ { - T } ) = P ( ( X _ { k + 1 | k } - \bar { X } _ { k + 1 | k} ) ( X _ { k + 1 | k } - \bar { X } _ { k + 1 | k } ) ^ T ) $$

$$ \large P _ { k + 1 | k } = A E ( e _{ k | k } e _ { k | k } ^ T ) A ^ T + E ( F w _ k w _ k ^ T F ^ T ) $$

در نتیجه، انتشار کواریانس خطا به صورت زیر است:

$$ \large P _ { k + 1 | k } = A P _ { k | k } A ^ T + F Q F ^ T . $$

۲. به‌روزرسانی

اکنون کوواریانس تخمین حالت‌ها را پس از اندازه‌گیری به‌روز می‌کنیم. اندازه‌گیری به صورت زیر است:

$$ \large Y _ { k + 1 } = C X _ { k + 1 | k } + D u _ { k + 1 } + v _ { k + 1 } $$

امید ریاضی اندازه‌گیری برابر است با:

$$ \large \hat { Y } _ { k + 1 } = C \hat { X } _ { k + 1 | k } + D u _ { k + 1 } . $$

خطای بین تخمین حالت و میانگین نیز به صورت زیر نوشته می‌شود:

$$ \large Y _ { k + 1 } - \hat { Y } _ { k + 1 } = C X _ { k + 1 | k } + D u _ { k + 1 } + v _ { k + 1 } - ( C \hat { X } _ { k + 1 | k } + D u _ { k + 1 } ) $$

$$ \large e _ { Y , k + 1 } = C e _ { k + 1 | k } + v _ { k + 1 } $$

کوواریانس خطای اندازه‌گیری قبل از انجام اندازه‌گیری برابر است با:

$$ \large \begin{align*}
E ( e _ { Y , k + 1 } e _ { Y , k + 1 } ^ T ) & = E ( ( C e _ { k + 1 | k } + v _ { k + 1 } ) ( C e _ { k + 1 | k } + v _ { k + 1 } ) ^ T ) \\
E ( e _ { Y , k + 1} e _ { Y , k + 1 } ^ T ) & = E ( ( C e _ { k +1 | k } + v _ { k + 1} ) ( e_ { k + 1 | k } ^ T C ^ T + v _ { k + 1 } ^ T ) ) \\
& = C P _ { k + 1 | k } C^ T + R
\end{align*} $$

به‌روزرسانی حالت پس از اندازه‌گیری

حالت پس از اندازه‌گیری به صورت زیر به‌روزرسانی می‌شود:

$$ \large \begin{align*}
\hat { X } _ { k + 1 | k + 1 } & = \hat { X } _ { k + 1 | k } + K _ { k + 1 } ( Y _ { k +1 } - ( C \hat { X } _ { k + 1 | k } + D u _ { k + 1 } ) ) \\
\hat { X } _ { k + 1 | k + 1 } & = \hat { X } _ { k + 1 | k } + K _ { k + 1 } e _ { Y , k + 1 } \\
\hat { X } _ { k + 1 | k + 1 } & = \hat { X } _ { k + 1 | k } + K _ { k + 1 } C e _ { k + 1 | k } + K _ { k + 1 } v _ { k + 1 }
\end {align*} $$

یعنی تخمین حالت بر اساس خطای بین اندازه‌گیری واقعی و اندازه‌گیری چشم‌داشتی تخمین حالت به‌روز می‌شود. هدف، یافتن $$ K _ {k+1}$$ به گونه‌ای است که اختلاف بین حالت واقعی و تخمین آن کمینه شود.

می‌خواهیم بهره‌ای را به گونه‌‌ای انتخاب کنیم که خطای بین تخمین حالت پسین (عقبی)‌ و حالت واقعی را کمینه کند.

$$ \large \begin{align*}
X _ { k + 1 } - \hat { X } _ { k + 1 | k + 1 } & = X _ { k + 1 } - \hat { X } _ { k + 1 | k } - K _ { k + 1 } C e _ { k + 1 | k } -K _ { k + 1 } v _ { k + 1 } \\
e _ { k + 1 | k + 1 } & = ( I - K _ { k + 1 } C ) e _ { k + 1 | k } - K _ { k + 1 } v _ { k + 1 }
\end {align*} $$

بنابراین، کوواریانس پسین برابر است با:

$$ \large \begin{align*}
P _ { k + 1 | k + 1 } & = E ( e _ { k + 1 | k + 1 } e _ { k + 1 | k + 1 } ^ T ) \\
& = E \left ( ( (I - K _ { k + 1 } C ) e _ { k + 1 | k } - K _ { k + 1 } v _ { k + 1 } ) ( ( I - K _ { k + 1 } C ) e _ { k + 1 | k } - K _ { k + 1 } v _ { k + 1 } ) ^ T \right ) \\
& = ( I - K _ { k + 1 } C ) E ( e _ { k + 1 | k } e _ { k + 1 | k } ^ T ) ( I - K _ { k + 1 } C ) ^ T + K _ { k + 1 } E ( v _ { k + 1 } v _ { k + 1 } ^ T ) K _ { k + 1} ^ T \\
P _ { k + 1 | k + 1 } & = ( I - K _ { k + 1 } C ) P _ { k + 1 | k } ( I - K _ { k + 1 } C ) ^ T + K _ { k + 1 } R K _ { k + 1 } ^ T \\
P _ { k + 1 | k + 1 } & = ( I - K _ { k + 1 } C ) P _ { k + 1 | k } ( I - K _ { k + 1 } C ) ^ T + K _ { k + 1 } R K _ { k + 1 } ^ T \\
P _ { k + 1 | k + 1 } & = P _ { k + 1 | k } - K _ { k + 1 } C P _ { k + 1 | k } - P _ { k + 1 | k } C ^ T K _ { k + 1 } ^ T + K _ { k + 1 } ( C P _ { k + 1 | k } C ^ T + R ) K _ { k + 1 } ^ T
\end {align*} $$

از آنجایی که اثر ماتریس کوواریانس خطای بین تخمین حالت و به‌ روز رسانی اندازه‌‌گیری است، بنابراین، ماتریس بهره‌ای که ماتریس کوواریانس را کمینه می‌کند، جواب بهینه است. با مشتق‌گیری نسبت به بهره، داریم:

$$ \large \frac { \partial tr ( P _ { k + 1 | k + 1 } ) } { \partial K _ { k + 1 } } = - 2 ( C P _ { k + 1 | k } ) ^ T + 2 K _ { k +1 } ( C P _ { k + 1 | k } C ^ T + R ) = 0 $$

در نتیجه:

$$ \large K _ { k + 1 } = P _ { k + 1 | k } C ^ T ( C P _ { k + 1 | k } C ^ T + R ) ^ { - 1 } $$

با جایگذاری $$ K_{k+1} $$ در عبارت کوواریانس پسین، داریم:

$$ \large P _ { k + 1 | k + 1 } = P _ { k + 1 | k } - K _ { k + 1 } C P _ { k + 1 | k } - K _ { k + 1 } C ^ T P _ { k + 1 | k } ^ T + P _ { k + 1 | k } C ^ T ( C P _ { k + 1 | k } C ^ T + R ) ^ { - 1 } ( C P_ { k + 1 | k } C ^ T + R ) K _ { k + 1 } ^ T $$

$$ \large P _ { k + 1 | k + 1 } = P _ { k + 1 | k } - K _ { k + 1 } C P _ { k + 1 | k } - K _ { k + 1 } C ^ T P _ { k + 1 | k } ^ T + P _ { k + 1 | k } C ^ T K _ { k + 1 } ^ T $$

$$ \large P _ { k + 1 | k + 1 } = P _ { k + 1 | k } - K _ { k + 1 } C P _ { k + 1 | k } = ( I - K _ { k + 1 } C ) P _ { k + 1 | k } $$

فرم نهایی فیلتر کالمن

فرم نهایی الگوریتم فیلتر کالمن به صورت زیر است:

۱. انتشار حالت

$$ \large \hat { X } _{ k + 1 | k } = A \hat { X } _ {k | k } + B u _ k $$

$$ \large P _ { k + 1 | k } = A P _ { k | k } A ^ T + F Q F ^ T . $$

فیلم آموزش کنترل بهینه در فرادرس

کلیک کنید

۲. به‌روزرسانی اندازه‌گیری

$$ \large e _ { Y , k + 1 } = y ( k + 1 ) - ( C \hat { X } _ {k + 1 | k } + D u _ { k + 1 } ) $$

$$ \large S _ { k + 1 } = ( C P _ { k + 1 | k } C ^ T + R ) $$

$$ \large K _ { k + 1 } = P _ { k + 1 | k } C ^ T S _ { k + 1 } ^ { - 1 } $$

$$ \large \hat { X } _ { k + 1 | k + 1 } = \hat { X } _ { k + 1 | k } + K _{ k + 1 } e _ { Y , k + 1 } $$

$$ \large P _ { k + 1 | k + 1 } = ( I - K _ { k + 1 } C ) P _ { k + 1 | k } $$

فیلتر کالمن در متلب (گسسته)

در این بخش، مثال‌هاییی از پیاده‌سازی فیلتر کالمن در متلب (گسسته) را ارائه خواهیم کرد.

فیلم آموزش کنترل مدرن و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

مثال ۱

ابتدا فیلتر کالمن را برای تخمین حالت‌ها در ساده‌ترین مورد که یک فرایند و اندازه‌گیری قطعی داریم، اعمال می‌‌کنیم. سیستم زیر را در نظر بگیرید:

$$ \large \ddot{X} = u$$

که اندازه‌گیری $$ y = X $$ است. می‌خواهیم یک مشاهده‌گر را به گونه‌ای تشکیل دهیم که $$ \hat{X} \rightarrow X $$.

سیستم را به صورت زیر تقریب می‌زنیم:

$$ \large \begin{align*}
X _ 1 ( t + 1 ) & = X _ 1 ( t ) + \delta t X _ 2 \\
X _ 2 ( t + 1 ) & = \delta t u
\end {align*} $$

اندازه‌گیری به صورت زیر تقریب زده می‌شود:

$$ \large y = X + v $$

که در آن، $$ v $$ یک فرایند گاوسی با میانگین صفر و واریانس $$ 10 ^ { - 8 } $$ است. توجه کنید از آنجایی که سیستم قطعی است، از یک مقدار بسیار کوچک کوواریانس اندازه‌گیری $$R$$ استفاده می‌کنیم. برنامه زیر، پیاده‌سازی فیلتر کالمن در متلب را برای تخمین حالت نشان می‌دهد. از آنجایی که کواریانس حالت‌ها را از قبل نمی‌دانیم، در ابتدا فرض می‌کنیم یک ماتریس واحد باشد. حالت‌ها در یک تکرار تخمین زده می‌شوند و خطا سریعاً به صفر میل می‌کند.

1clc
2close all
3clear all
4
5
6A = [0 1 ; 0 0];
7B = [0 ; 1];
8dt = 0.001;
9
10Ad = eye(2) + dt*[0 1 ; 0 0];
11Bd = dt*B;
12
13C = [1 0];
14R = 1e-8;
15Q = 0*eye(2);
16P_pl = eye(2);
17X_hat_0 = [0;0];
18
19X_0 = [1;0];
20
21X(:,1)= X_0;
22Y(1) = C*X(:,1);
23t(1) = 0;
24X_hat(:,1)= X_hat_0;
25
26for i = 1:2000
27    u = 1;
28    
29    t(i+1) = t(i)+dt;
30    
31    % True process 
32    X(:,i+1)=Ad * X(:,i) + Bd*u;
33    Y(i+1) = C*X(:,i+1);
34    
35    P_mi = Ad*P_pl*Ad' + Q;
36    X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
37    
38    
39    Y_hat(i+1) = C*X_hat(:,i+1);
40    
41    
42    e_Y  = Y(i+1) - Y_hat(i+1);
43    S = C*P_mi*C'+R;
44    K = P_mi*C'*inv(S);
45    P_pl = (eye(2) - K*C)*P_mi;
46    X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
47end

1figure;
2subplot(2,1,1)
3plot(t,X(1,:),t,X_hat(1,:),'--')
4subplot(2,1,2)
5plot(t,X(2,:),t,X_hat(2,:),'--')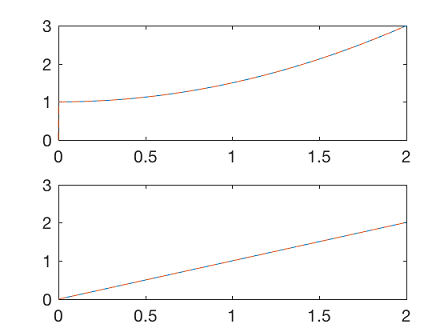

مثال ۲

از فیلتر کالمن می‌توان برای تخمین پارامتر نیز استفاده کرد. سیستم دینامیکی زیر را در نظر بگیرید:

$$ \large \begin{align*}
\large \dot { X _ 1 } & = X _ 2 + \alpha \\
\dot { X _ 2 } & = u
\end {align*} $$

که در آن، $$ \alpha$$ پارامتری نامعلوم است. تنها اندازه‌گیری $$ y = X_1 + v $$ را داریم که در آن، $$ v$$ یک فرایند گاوسی با واریانس $$ R = 0.1 $$ است. می‌توانیم از فیلتر کالمن استفاده کرده و پارامتر نامعلوم را تخمین بزنیم. ابتدا یک حالت جدید به سیستم اضافه می‌کنیم که خودش یک پارامتر است. همچنین دینامیکی را معرفی می‌کنیم که مشتق آن برابر با صفر است. از آنجایی که پارامتر را به صورت دقیق نمی‌دانیم، یک جمله نویز به دینامیک سیستم اضافه می‌کنیم تا نامعینی در مدل لحاظ شود.

$$ \large \begin{align*}
X _ 1 ( t + 1 ) & = X _ 1 ( t ) + \delta t X _ 2 (t)+ \delta t X _ 3(t) \\
X _ 2 ( t + 1 ) & = \delta t u \\
X _ 3 ( t + 1 ) & = X _ 3 ( t ) + w ( t )
\end {align*} $$

در معادلات بالا، $$ w (t)$$ یک فرایند گاوسی با کوواریانس $$ 10^{-4} $$ است. معادلات بالا را می‌توان به فرم زیر نوشت:

$$ \large X _ { t + 1 } = A X _ { t } + B u _ { t } + F w _ t $$

که در آن:

$$ \large
A = \left [ \begin {array} {ccc} 1 & \delta t & \delta t \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end {array} \right ] , \;\;\;\;\;\;\;
B = \left [ \begin {array} {c} 0 \\ \delta t \\ 0 \end {array} \right ] ,
\;\;\;\;\;\;\;
F = \left [ \begin {array} {c} 0 \\ 0 \\ 1 \end {array} \right ] $$

در ابتدا، کوواریانس حالت را نمی‌دانیم، بنابراین تقریب آن را ۱ در نظر می‌گیریم. البته، اندازه‌گیری دقیق کوواریانس برای تخمین حالت لازم است. بنابراین، شبیه‌سازی را یک بار برای تخمین کوواریانس اجرا می‌کنیم و دوباره آن را اجرا کرده و این فرایند را تکرار می‌کنیم. با تکرار چندباره این فرایند (معمولاً دو بار)، یک تخمین مناسب از پارامتر نامعلوم خواهیم داشت.

1clc
2close all
3clear all
4
5
6A = [0 1 1; 0 0 0;0 0 0];
7B = [0 ; 1;0];
8
9dt = 0.001;
10
11Ad = eye(3) + dt*A;
12Bd = dt*B;
13F = [0;0;1];
14
15C = [1 0 0];
16R = .1;
17Q = diag([1e-4]);
18P_pl = eye(3);
19
20X_hat_0 = [0;0;0];
21X_0 = [1;0;10];
22
23X(:,1)= X_0;
24Y(:,1) = C*X(:,1);
25t(1) = 0;
26X_hat(:,1)= X_hat_0;
27
28for i_sim = 1:2
29    A_sim(i_sim) = X_hat(3,1);
30    for i = 1:2500
31        u = .5;
32        
33        t(i+1) = t(i)+dt;
34        
35        % True process
36        X(:,i+1)=Ad * X(:,i) + Bd*u;
37        Y(:,i+1) = C*X(:,i+1) + sqrt(R)*randn(1,1);
38        
39        % Observer model
40        % Prediction based on system dynamics
41        P_mi = Ad*P_pl*Ad' + F*Q*F';
42        X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
43        Y_hat(:,i+1) = C*X_hat(:,i+1);
44        
45        % Update based on measurement
46        e_Y  = Y(:,i+1) - Y_hat(:,i+1);
47        S = C*P_mi*C'+R;
48        K = P_mi*C'*inv(S);
49        P_pl = (eye(3) - K*C)*P_mi;
50        X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
51    end
52    X_hat(3,1) = X_hat(3,end);
53    
54end

1figure;
2subplot(2,1,1)
3plot(t,X(1,:),t,X_hat(1,:),'--')
4axis([0 2.5 0 40])
5xlabel('time')
6ylabel('Position')
7
8subplot(2,1,2)
9plot(t,X(2,:),t,X_hat(2,:),'--')
10xlabel('time')
11ylabel('Velocity')
12axis([0 2.5 0 2])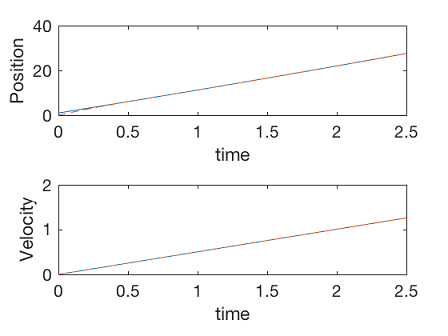

1figure;
2plot(t,X(3,:),t,X_hat(3,:),'--')
3axis([0 2.5 0 12.5])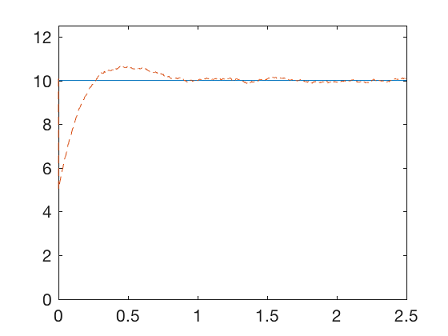

مثال ۳

همان‌طور که گفتیم، از فیلتر کالمن می‌توان برای تخمین پارامتر استفاده کرد. باز هم سیستم زیر را در نظر بگیرید:

$$ \large \begin{align*}
\dot { X _ 1 } & = X _ 2 + \alpha \\
\dot { X _ 2 } & = u
\end {align*} $$

که در آن، $$ \alpha $$ پارامتری نامعلوم است. اندازه‌گیری‌های $$ y_1 = X_1 + v_1 $$ و $$ y_2 = X_2 + v_2 $$ نیز در دسترس هستند، که در آن‌ها $$v_1$$ و $$v_2$$ فرایندهای گوسی با واریانس‌های $$ R_1 = 0.1$$ و $$ R_ 2 = 0.1 $$ هستند. می‌توانیم از فیلتر کالمن استفاده کنیم و پارامتر نامعلوم را تخمین بزنیم:‌

$$ \large \begin{align*}
X _ 1 ( t + 1 ) & = X _ 1 ( t ) + \delta t X _ 2 + \delta t X _ 3 \\
X _ 2 ( t + 1 ) & = \delta t u \\
X _ 3 ( t + 1 ) & = X _ 3 ( t ) + w ( t )
\end {align*} $$

که در آن، $$ w ( t) $$ یک فرایند گوسی با کوواریانس $$ 10^{-4} $$ است. مانند مثال قبل، شبیه‌سازی را یک بار برای تخمین کوواریانس اجرا کرده و سپس فرایند را دوباره تکرار می‌کنیم. با تکرار چندباره این فرایند (معمولاً دو بار)، به یک تخمین مناسب برای پارامتر نامعلوم می‌رسیم.

1clc
2close all
3clear all
4
5
6A = [0 1 1; 0 0 0;0 0 0];
7B = [0 ; 1;0];
8dt = 0.001;
9
10Ad = eye(3) + dt*A;
11Bd = dt*B;
12
13
14F = [0;0;1];
15
16C = [1 0 0;
17     0 1 0];
18R = diag([.1 .1]);
19Q = diag([1e-4]);
20P_pl = eye(3);
21
22X_hat_0 = [0;0;0];
23X_0 = [1;0;10];
24
25X(:,1)= X_0;
26Y(:,1) = C*X(:,1);
27t(1) = 0;
28X_hat(:,1)= X_hat_0;
29
30for i_sim = 1:1
31    A_sim(i_sim) = X_hat(3,1);
32    for i = 1:2500
33        u = .5;
34        
35        t(i+1) = t(i)+dt;
36        
37        % True process
38        X(:,i+1)=Ad * X(:,i) + Bd*u;
39        Y(:,i+1) = C*X(:,i+1) + sqrt(R)*randn(2,1);
40        
41        
42        % Observer model
43        % Prediction based on system dynamics
44        P_mi = Ad*P_pl*Ad' + F*Q*F';
45        X_hat(:,i+1)=Ad * X_hat(:,i) + Bd*u;
46        Y_hat(:,i+1) = C*X_hat(:,i+1);
47        
48        % Update based on measurement
49        e_Y  = Y(:,i+1) - Y_hat(:,i+1);
50        S = C*P_mi*C'+R;
51        K = P_mi*C'*inv(S);
52        P_pl = (eye(3) - K*C)*P_mi;
53        X_hat(:,i+1)=X_hat(:,i+1) + K*e_Y;
54    end
55    X_hat(3,1) = X_hat(3,end);
56    
57end

1figure;
2subplot(2,1,1)
3plot(t,X(1,:),t,X_hat(1,:),'--')
4axis([0 2.5 0 40])
5xlabel('time')
6ylabel('Position')
7
8subplot(2,1,2)
9plot(t,X(2,:),t,X_hat(2,:),'--')
10xlabel('time')
11ylabel('Velocity')
12axis([0 2.5 0 2])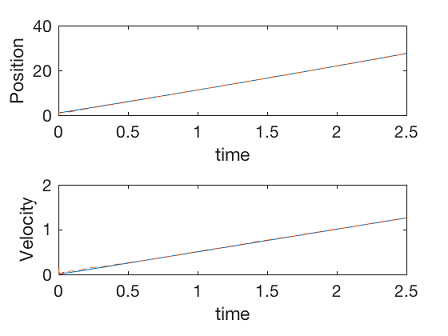

1figure;
2plot(t,X(3,:),t,X_hat(3,:),'--')
3axis([0 2.5 0 12.5])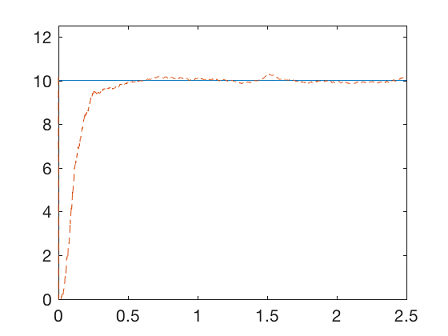

فیلتر کالمن پیوسته

فیلتر کالمن-بوسی (Kalman-Bucy Filter) معادل پیوسته‌زمان فیلتر کالمن است. استخراج و تحلیل فیلتر کالمن برای سیستم‌های پیوسته‌زمان دشوار است، زیرا اندازه‌گیری و حالت‌ها متغیرهایی پیوسته‌اند و به‌روزرسانی پیشین و پسین به صورت شفاف تعریف نشده‌اند. با این حال، با گسسته‌سازی فیلتر پیوسته و میل دادن زمان گسسته‌سازی به صفر، معادلات فیلتر کالمن به دست می‌آیند. در ادامه، این روش را توضیح می‌دهیم.

فرض کنید دینامیک سیستم به صورت زیر است:

$$ \large \dot { X } = A X + B u + F w $$

که در آن، $$w$$ یک فرایند گاوسی با میانگین صفر و کوواریانس $$Q$$ است و اندازه‌گیری به صورت زیر بیان می‌شود:

$$ \large y = C X + D u + v $$

فیلتر تخمین زننده حالت از دو معادله دیفرانسیل تشکیل شده است:

$$ \large \begin{align*}
\dot { \hat { X } } & = A \hat { X } + B u + K ( y - C \hat { X } + D u ) \\
\dot { P } & = A P + P A ^ T + F Q F ^ T - K R K ^ T \\
K & = P C ^ T R ^ { - 1 } \\
\dot { P } & = A P + P A ^ T + F Q F ^ T - P C ^ T R C P
\end {align*} $$

لازم به ذکر است که در مورد پیوسته فیلتر کالمن، کوواریانس خطای اندازه‌گیری و کوواریانس پیشین، هر دو، $$R$$ هستند. علاوه بر این، در محاسبات بهره مشاهده‌گر معکوس ماتریس کوواریانس نویز $$R$$ به کار می‌رود. بنابراین، اگر دو سنسور داشته باشیم که یکی بسیار نویزدار و دیگری بسیار دقیق باشد، فیلتر کالمن مقدار بیشتری را روی سنسور دقیق قرار می‌دهد؛ یعنی سنسوری که نویز پایین‌تری دارد، سهم بیشتری در به‌روزرسانی خواهد داشت. دقت کنید که معادله فوق، مشابه معادله ریکاتی است که در رگولاتور مرتبه دوم خطی به دست می‌آید و می‌توانیم آن را با تکنیکی مشابه حل آن حل کنیم. در مورد خاص زمان بی‌نهایت، معادله ریکاتی به صورت زیر در خواهد آمد:

$$ \large 0 = A P + P A ^ T + F Q F ^ T - P C ^ T R C P $$

معادله بالا مشابه معادله ریکاتی جبری است که در آن، به جای $$A$$ و $$B$$، ماتریس‌های $$A^T$$ و $$ C^T$$ قرار دارند و می‌توان آن‌ را با دستور "care" در متلب حل کرد.

فیلتر کالمن در متلب (پیوسته)

در این بخش، چند مثال از پیاده‌سازی فیلتر کالمن در متلب (پیوسته) را ارائه خواهیم کرد.

مثال ۴

سیستمی با معادله $$ \ddot{x} = u $$ را در نظر بگیرید که تنها موقعیت آن اندازه‌گیری می‌شود. می‌خواهیم با فرض اینکه کوواریانس نویز اندازه‌گیری واحد بوده و برابر با کوواریانس فرایند است، یک فیلتر کالمن پیوسته برای سیستم ارائه کنیم. برای این منظور، از دستور متلب برای حل معادله ریکاتی استفاده شده است.

1clc
2close all
3clear all
4
5
6A = [0 1;0 0];
7B = [0; 1];
8C = [1 0];
9
10t = 0:0.001:20; 
11dt = t(2) - t(1);
12X(:,1) = [1;0];
13y(:,1) = C*X;
14R_k = diag([1 ]);
15Q_k = diag([1 1]);
16P_k = care(A',C',Q_k,R_k);
17K_k = P_k*C'*inv(R_k);
18L = K_k;
19
20X_hat(:,1) = [0;0];
21y_hat(:,1) = C*X_hat;
22for i = 2:length(t)
23    u = .5;
24    
25    X(:,i) = X(:,i-1)  +dt * (A*X(:,i-1) + B*u);
26    y(:,i) = C*X(:,i) + sqrt(R_k)*randn(size(C,1),1);
27
28    X_hat(:,i) = X_hat(:,i-1)  +dt * (A*X_hat(:,i-1) + B*u +L *(y(:,i-1)-y_hat(:,i-1)));
29    y_hat(:,i) = C*X_hat(:,i) ;
30end
31
32
33figure;
34subplot(2,1,1)
35plot(t,X(1,:),t,X_hat(1,:))
36legend('Actual','Estimate')
37xlabel('time')
38ylabel('Position')
39subplot(2,1,2)
40plot(t,X(2,:),t,X_hat(2,:))
41xlabel('time')
42ylabel('Velocity')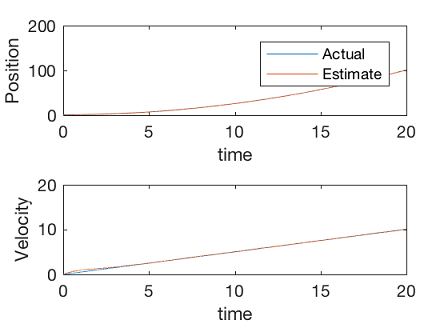

مثال ۵

سیستم مثال قبل، یعنی $$ \ddot{x} = u $$ را در نظر بگیرید که اکنون دو سنسور برای اندازه‌گیری موقعیت دارد: یکی بسیار دقیق (با کوواریانس ۰٫۰۱) و دیگری غیردقیق (با کوواریانس ۱). با فرض اینکه کواریانس فرایند یک ماتریس یکه است، یک فیلتر کالمن برای سیستم ارائه می‌کنیم. با استفاده از دستور "care" در متلب می‌توان برای حل معادله ریکاتی استفاده کرد. بهره‌هایی که از معادله ریکاتی حالت ماندگار به دست می‌آید به صورت زیر است:

$$ \large
K _ k = \left [ \begin {array} {cc} 0 . 1 0 9 0 & 10.8956 \\ 0.0995 & 9.9504 \end{array} \right ] $$

ماتریس بهره فیلتر کالمن اهمیت بیشتری به داده‌های سنسور دقیق‌تر می‌دهد.

1clc
2close all
3clear all
4
5
6A = [0 1;0 0];
7B = [0; 1];
8C = [1 0;
9    1 0];
10
11t = 0:0.001:20; 
12dt = t(2) - t(1);
13X(:,1) = [1;0];
14y(:,1) = C*X;
15R_k = diag([1 .01]);
16Q_k = diag([1 1]);
17P_k = care(A',C',Q_k,R_k);
18K_k = P_k*C'*inv(R_k);
19L = K_k;
20K_k
21X_hat(:,1) = [0;0];
22y_hat(:,1) = C*X_hat;
23for i = 2:length(t)
24    u = .5;
25    
26    X(:,i) = X(:,i-1)  +dt * (A*X(:,i-1) + B*u);
27    y(:,i) = C*X(:,i) + sqrt(R_k)*randn(size(C,1),1);
28
29    X_hat(:,i) = X_hat(:,i-1)  +dt * (A*X_hat(:,i-1) + B*u +L *(y(:,i-1)-y_hat(:,i-1)));
30    y_hat(:,i) = C*X_hat(:,i) ;
31end
32
33
34figure;
35subplot(2,1,1)
36plot(t,X(1,:),t,X_hat(1,:))
37legend('Actual','Estimate')
38xlabel('time')
39ylabel('Position')
40subplot(2,1,2)
41plot(t,X(2,:),t,X_hat(2,:))
42xlabel('time')
43ylabel('Velocity')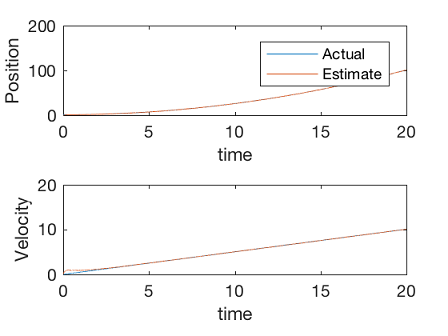

کنترل گاوسی درجه دو خطی

کنترل گاوسی درجه دوم خطی یک رویکرد کنترلی است که از رگولاتور درجه دوم خطی (LQR) برای کنترل و برای فیلتر کالمن به منظور تخمین استفاده می‌کند. با توجه به اصل تفکیک تخمین و کنترل، می‌توانیم مشاهده‌گر و کنترل‌کننده را بدون اثرگذاری روی هم به صورت جداگانه طراحی کنیم. برنامه زیر، یک رگولاتور خطی مرتبه دوم برای کنترل و فیلتر کالمن پیوسته را با استفاده از دستور "care" متلب ارائه می‌دهد.

1clc
2close all
3clear all
4
5
6A = [0 1;0 0];
7B = [0; 1];
8C = [1 0];
9
10% Controller design
11R = diag([1]);
12Q = diag([1e-2 1e-2]);
13M_a = rank(ctrb(A,B));
14P = care(A,B,Q,R);
15K_u  = inv(R)*B'*P;
16
17t = 0:0.001:20; 
18dt = t(2) - t(1);
19X(:,1) = [1;0];
20y(:,1) = C*X;
21
22% Observer design
23R_k = diag([1 ]);
24Q_k = diag([1 1]);
25P_k = care(A',C',Q_k,R_k);
26K_k = P_k*C'*inv(R_k);
27L = K_k;
28
29X_hat(:,1) = [0;0];
30y_hat(:,1) = C*X_hat;
31for i = 2:length(t)
32    u = -K_u*X_hat(:,i-1);
33    
34    X(:,i) = X(:,i-1)  +dt * (A*X(:,i-1) + B*u);
35    y(:,i) = C*X(:,i) + sqrt(R_k)*randn(size(C,1),1);
36
37    X_hat(:,i) = X_hat(:,i-1)  +dt * (A*X_hat(:,i-1) + B*u +L *(y(:,i-1)-y_hat(:,i-1)));
38    y_hat(:,i) = C*X_hat(:,i) ;
39end
40
41
42figure;
43subplot(2,1,1)
44plot(t,X(1,:),t,X_hat(1,:))
45legend('Actual','Estimate')
46xlabel('time')
47ylabel('Position')
48subplot(2,1,2)
49plot(t,X(2,:),t,X_hat(2,:))
50xlabel('time')
51ylabel('Velocity')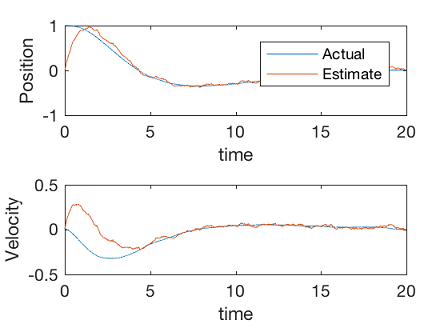

جمع‌بندی

فیلترهای کالمن کاربردهای فراوانی در کنترل و پردازش سیگنال دارند. این فیلترها رؤیت‌گرهای مشابه رگولاتورهای مرتبه دوم خطی هستند و می‌توان با استفاده از همان عبارات و با جایگزینی ماتریس سیستم با ترانهاده‌اش، و جایگزینی ماتریس ورودی با ترانهاده ماتریس اندازه‌گیری آن‌ها را به دست آورد. فیلترهای کالمن وقتی در فرایندها و اندازه‌گیری‌هایی به کار می‌روند که مبتنی بر توزیع گاوسی‌اند، بهینه هستند. فیلترهای کالمن را می‌توان برای سیستم‌های غیرخطی نیز بیان کرد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی کنترل
• آموزش کنترل مدرن به همراه پیاده سازی در متلب​‎
• مجموعه آموزش‌های مهندسی برق
• آموزش کنترل بهینه
• سیستم غیر خطی — راهنمای جامع
• کنترل بهینه در متلب — از صفر تا صد
• کنترل پیش بین مدل (MPC) — راهنمای جامع

^^