ضرب اعداد توان دار – آموزش به زبان ساده و با مثال

در زندگی روزمره، اعداد بزرگ و کوچک به وفور به کار برده می‌شوند. وزن یک کامیون بر حسب کیلوگرم، فاصله بین مولکول‌ها برحسب میلیمتر و غیره، نمایانگر استفاده از اعداد بزرگ و کوچک هستند. ولی برای نمایش این اعداد و اجرای عملیات ریاضی روی این اعداد ممکن است دچار مشکل شویم. یک روش برای نمایش چنین اعدادی، استفاده از اعداد توان دار است. در این متن به بررسی نحوه اجرای عملگر ضرب اعداد توان دار می‌پردازیم و به کمک مفاهیمی که معرفی خواهیم کرد، نحوه بدست آوردن حاصل ضرب دو عدد توان دار را مشخص می‌کنیم. هر چه توان اعداد، مقداری مثبت و بزرگ باشد، عدد حاصل نیز بزرگتر خواهد بود. ولی برای نمایش اعداد کوچک یا بسیار کوچک از توان‌های منفی کمک خواهیم گرفت.

بهتر است قبل از مطالعه این متن، به عنوان مقدمه و آشنایی با اعداد توان‌دار، مطالب اعداد توان دار — به زبان ساده و توضیح توان در ریاضیات — به زبان ساده از مجله فرادرس را بخوانید. همچنین خواندن نوشتارهای نماد علمی چیست؟ — به زبان ساده و جذر چیست ؟ — محاسبه رادیکال به زبان ساده از مجله فرادرس نیز خالی از لطف نیست.

ضرب اعداد توان دار

مجموعه اعداد صحیح، یکی از مجموعه اعدادی است که برای همگی ما شناخته شده است. اعداد صحیح، شامل اعداد مثبت و منفی است که به صورت یک عدد طبیعی به همراه یک علامت + یا - مشخص می‌شود. محاسبه و اجرای عملیات جبری روی چنین اعدادی به سادگی صورت گرفته و مفاهیم مربوط به آن‌ها بسیار ساده است. به همین جهت علاقمند هستیم که اعداد دیگر را هم به کمک این چنین روشی نمایش داده و در صورت امکان به کمک چهار عمل اصلی که برای اعداد صحیح وجود دارد، روی اعداد دیگر نیز همین عملیات را اجرا کنیم.

نکته: نمایش اعداد توان دار در ماشین حساب گاهی اوقات به کمک دکمه EXP امکان پذیر است. ولی گاهی نیز از این دکمه برای نمایش عدد نپر استفاده شده و توان‌های آن محاسبه خواهد شد.

فرض کنید قرار است برای نمایش چهار بار ضرب عدد ۲ در خودش، از یک نماد کمک بگیریم. این نماد به صورت یک عدد توان دار خواهد بود. به این ترتیب تساوی زیر را نوشته و 8 که حاصل ضرب سه بار عدد ۲ در خودش است را نمایش می‌دهیم.

$$\large {\displaystyle 8 = 2 \times 2 \times 2 = 2^3 = 8 }$$

اگر بخواهیم عدد 81 را به صورت عدد توان دار بنویسیم به صورت زیر خواهد بود. توجه داشته باشید که در این حالت، 81 را به صورت تجزیه به عامل‌های اول نمایش داده‌ایم.

$$\large {\displaystyle 81 = 3 \times 3 \times 3 \times 3= 3^4 = 81 }$$

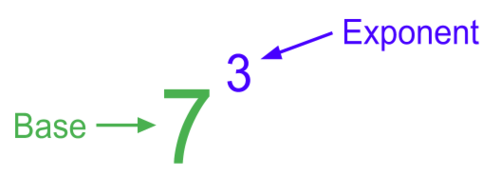
همانطور که گفتیم، اعداد توان دار یک روش برای نمایش اعداد بسیار بزرگ یا بسیار کوچک است. در حقیقت نماد علمی نیز نوعی عدد توان دار محسوب می‌شود. هر عدد توان دار دو مشخصه اصلی دارد. در تصویر زیر این بخش‌ها را به خوبی مشاهده می‌کنید.

عددی که در تصویر بالا می‌بینید، به شکل دو به توان سه می‌خوانیم.

در تصویر بالا به خوبی می‌بینید که ۲ پایه و ۳ نیز توان است. منظور از پایه، عددی است که باید به توان برسد و نما نیز عددی است که مقدار توان یا تعداد تکرار عمل ضرب پایه در خودش را مشخص می‌کند. البته هنوز از اعداد بزرگ یا کوچک استفاده نکرده‌ایم ولی اگر لازم باشد، مقدار توان را افزایش خواهیم داد تا چنین اعدادی قابل نمایش و استفاده باشند.

اغلب در بحث مربوط به اعداد صحیح، توان نشانگر تعداد ضرب است ولی اگر توان، مقداری صحیح نباشد، آن را نمی‌توان تعداد ضرب عدد پایه در خودش در نظر گرفت.

همانطور که گفتیم، اعداد توان دار را با دو مولفه یا پارامتر نشان می‌دهند. ابتدا پایه (base) را نوشته و به صورت یک اندیس بالا، توان (exponent) را می‌نویسند. بنابراین اگر $$a$$ را پایه و $$b$$ را توان بنامیم، یک عدد توان دار را به صورت زیر نمایش خواهیم داد.

$$\large {\displaystyle a^b }$$

فیلم آموزش ریاضی صنف هفتم – ویژه دانش آموزان افغانستانی (رایگان) در فرادرس

کلیک کنید

فرض کنید بخواهیم ضرب عدد 64 را در 729 مشخص کنیم. توجه داشته باشید که این دو عدد را به صورت توان‌هایی از ۲ و ۳ می‌توان نمایش داده و ضرب آن‌ها نیز برهمین اساس خواهیم نوشت.

$$\large {\displaystyle 64 \times 729 = 2^6 \times 3^6 = (2 \times 3 )^6 = }$$

$$\large {\displaystyle 6^6 = 46656 }$$

در ادامه قوانین مربوط به ضرب اعداد توان دار را مشخص خواهیم کرد تا به کمک آن‌ها، به سادگی و سرعت زیاد، عمل ضرب را برای چنین اعدادی آموزش دهیم.

برای آنکه با قواعد ضرب اعداد توان دار آشنا شوید، آن‌ها را به دو بخش تفکیک کرده‌ایم. ابتدا ضرب را برای اعداد شرح می‌دهیم که دارای توان‌های برابر ولی پایه‌های نابرابر باشند. سپس همین عمل را برای اعداد توان دار با پایه‌های برابر ولی توان‌های نابرابر اجرا خواهیم کرد.

ضرب اعداد توان دار با توان برابر

همانطور که در مثال قبل خواندید، اگر اعداد توان‌دار، توان‌های یکسانی داشته باشند، حاصل ضرب آن‌ها به صورت ضرب پایه‌ها به توان یکی از آن‌ها محاسبه می‌شود. پس کافی است ابتدا پایه‌ها را در هم ضرب کنیم، سپس به توان یکی از آن‌ها (که البته می‌دانیم با یکدیگر برابر هستند) برسانیم. به مثال‌های زیر دقت کنید.

$$\large {\displaystyle 2^3 \times 5^3 = (2 \times 5 )^3 = 1 0^3 = 1 0 0 0 }$$

$$\large {\displaystyle 3^3 \times 10^3 = (3 \times 1 0 )^3 = }$$

$$\large {\displaystyle 3 0^3 = 2 7 0 0 0 }$$

$$\large {\displaystyle 8 0^2 \times 1 2 5^2 = (8 0 \times 1 2 5 )^2 =}$$

$$\large {\displaystyle 10 0 0 0^2 = 1 0 0 0 0 0 0 0 0}$$

همانطور که در مثال‌های قبل مشاهده کردید، نمایش یک عدد بزرگ مثل ۱۰۰۰۰۰۰۰۰ به صورت ضرب دو عدد توان دار کوچکتر میسر است. به این ترتیب هم نمایش و هم عملیات بعدی ممکن است بر اساس این اعداد ساده‌تر صورت گیرد. از طرفی این عدد را به صورت یک عدد توان دار نیز به شکل زیر می‌توان مشخص کرد.

$$\large {\displaystyle 1 0 0 0 0 0 0 0 0 = 10 ^8 }$$

به صورت یک قانون کلی برای ضرب اعداد توان دار به صورت $$a^b$$ و $$c^b$$‌ که توان‌های یکسانی (یعنی $$b$$) دارند، از رابطه زیر کمک خواهیم گرفت.

$$\large {\displaystyle a^b \times c^b = (a \times c )^b }$$

مثال‌های بالایی چنین فرمولی را تایید می‌کنند.

ضرب اعداد توان دار با پایه برابر

این بار حالتی را در نظر می‌گیریم که در ضرب اعداد توان دار پایه‌ها برابر بوده ولی توان‌ها با هم فرق داشته باشند. فرض کنید عدد اول به صورت $$a^b$$ بوده و عدد دوم نیز به شکل $$a^c$$ نوشته شده. حاصل ضرب این دو عدد با توجه به اینکه پایه‌ها برابر است به صورت همان پایه و جمع توان‌ها خواهد بود. به رابطه زیر توجه کنید.

$$\large {\displaystyle a^b \times a^c = a^{( b + c)} }$$

به عنوان مثال، تساوی‌های زیر را در نظر بگیرید.

$$\large {\displaystyle 2^3 \times 2^3 = 2^{( 3 + 3 )} = 2^ 6 = 64 }$$

$$\large {\displaystyle 3^3 \times 3^{10} = 3^{(3 + 10 )} = 3^{13} }$$

$$\large {\displaystyle 8 0^2 \times 40^2 = (2 \times 40 )^ 2 \times 40^2 = }$$

$$\large {\displaystyle 2^2 \times 40^2 \times 40^2 = 2^2 \times 40^4 }$$

همانطور که در مثال آخر مشاهده می‌کنید، ممکن است که بعضی از اعداد به صورتی مطرح شوند که به نظر برسد پایه‌ها با یکدیگر تفاوت دارند ولی به کمک تجزیه یا فاکتورگیری می‌توانیم در ضرب اعداد توان دار به شکل عمل کنیم که پایه‌های یا نماها یکسان شده و از قاعده ضرب اعداد توان دار استفاده کنیم.

نکته: اگر یک عدد توان دار را به تعداد m‌ بار در خودش ضرب کنیم، می‌توان آن را به صورت توانی از یک عدد توان دار نشان دهیم. به رابطه زیر توجه کنید.

$$\large {\displaystyle a^b \times a^b \times a^b \times a^b = a^{ (b + b + b + b )} =}$$

$$\large {\displaystyle ( a^b)^ 4 = a^{4 b} }$$

به این ترتیب برای محاسبه $$(a^b)^c$$ می‌توان پایه را نوشت و توان‌ها را در هم ضرب کرد. پس قاعده کلی را به شکل زیر در می‌آوریم.

$$\large {\displaystyle \overbrace{ a^b \times a^b \times\ldots \times a^b \times a^b }^{ c \; \text{ times}} =}$$

$$\large {\displaystyle a^{ (\overbrace{ b + b + \ldots + b + b )}^{ c\; \text{ times}}} = a^{b c} =( a^b)^ c }$$

می‌دانید که ضرب یک عدد در خودش را مربع آن عدد می‌گوییم. به این ترتیب اگر هر دو عدد توان دار یکسان باشند (یعنی پایه و نمای یکسانی داشته باشند) ضرب آن‌ها، باعث می‌شود که به صورت مربع درآیند. به مثال زیر توجه کنید.

$$\large {\displaystyle 3^3 \times 3^3 = 3^{(3 + 3 )} = 3^{6} = 729 }$$

مشخص است که از قاعده پایه‌های یکسان، کمک گرفته‌ایم. ولی یکبار دیگر این عمل ضرب را به استفاده از قاعده توان‌های یکسان محاسبه می‌کنیم.

$$\large {\displaystyle 3^3 \times 3^3 = (3 \times 3 )^{3)} = 9^{3} = 729 }$$

همانطور که مشاهده می‌کنید، در صورتی که هر دو توان و پایه اعداد یکسان باشند، استفاده از هر دو قاعده، امکان‌پذیر بوده و نتیجه یکسانی از ضرب آن‌ها، حاصل می‌شود.

نکته: اگر عددی بدون توان ظاهر شود، به یاد داشته باشید که توان برای آن برابر با ۱ است. به این ترتیب در هنگام ضرب یک عدد توان دار با چنین عددی، کافی است که توان عدد اولی را یک واحد اضافه کنید. به مثال زیر دقت کنید.

$$\large {\displaystyle 5^3 \times 5 = 5^3 \times 5^1 = (5)^{(3 + 1)} = 5^{4} = 625 }$$

ضرب اعداد توان دار با توان منفی

تا اینجا مثال‌هایی که ارائه کردیم، اعداد توان دار با توان مثبت بود. ولی قواعدی که برای ضرب اعداد توان دار وجود دارد هم برای توان‌های مثبت و هم توان‌های منفی، برقرار است. به منظور روشن شدن بهتر موضوع به مثال‌های زیر توجه کنید.

$$\large {\displaystyle 2^{( - 3)} \times 5^{( - 3)} = (2 \times 5 )^{(- 3)} =}$$

$$\large {\displaystyle 10^{ (- 3)} = 0.0 0 1 }$$

$$\large {\displaystyle 3^{ (- 3)} \times 10^{ (- 3 )} = (3 \times 10 )^{(- 3) } =}$$

$$\large {\displaystyle 30^{( - 3)} = \dfrac{ 1}{ 2 7 0 0} }$$

$$\large {\displaystyle 8 0^{( - 2)} \times 1 2 5^{( - 2) } = (8 0 \times 1 2 5 )^{(- 2)} = }$$

$$\large {\displaystyle 10 0 0 0^{( -2)} = 0. 0 0 0 0 0 0 0 1 }$$

$$\large {\displaystyle 2^{( -3)} \times 2^3 = 2^{( 3 - 3 )} = 2^ 0 = 1}$$

$$\large {\displaystyle 3^3 \times 3^{(- 1 0 )} = 3^{(3 - 10 )} = 3^{(- 7) } =}$$

$$\large {\displaystyle \dfrac{ 1}{ 3^7} = 0. 0 0 0 4 5 7 2 4 7 }$$

چند قاعده کلی برای ضرب اعداد توان دار

در ادامه چند قاعده کلی را در مورد ضرب اعداد توان دار بیان می‌کنیم و آن‌ها را به صورت پارامتری نیز نشان خواهیم داد.

فیلم آموزش ریاضی – پایه نهم + گواهینامه در فرادرس

کلیک کنید

• اگر هم پایه‌ها و هم توان‌ها در هنگام ضرب اعداد توان‌دار یکسان هستند، می‌توانید از هر کدام از قواعد گفته شده استفاده کنید و نتیجه یکسانی نیز بگیرید. مشخص است که در این حالت هر دو عدد برابر هستند و حاصل ضرب، همان مربع یا توان دوم عدد توان دار است.

$$\large {\displaystyle a^b \times a^b = (a^ b)^2 = a^{ 2 b} = ( a \times a )^ b =}$$

$$\large {\displaystyle ( a^b )^2 }$$

• ضرب اعداد توان دار با عددی که توان آن صفر است، برابر با همان عدد خواهد بود. زیرا هر عدد به توان صفر، برابر با ۱ است.

$$\large {\displaystyle a^b \times c^0 = a^ b }$$

• ضرب اعداد توان دار با عددی که پایه آن صفر است، برابر با صفر خواهد بود. زیرا ضرب هر عدد در صفر برابر با صفر است.

$$\large {\displaystyle a^b \times 0^c = 0 }$$

• ضرب اعداد توان دار با توان‌های یکسان ولی پایه‌های غیریکسان، برابر با حاصل ضرب پایه‌ها به توان یکی از آن‌ها است.

$$\large {\displaystyle a^b \times c^b = (a \times c )^b }$$

• ضرب اعداد توان دار با پایه‌های یکسان، برابر با عدد پایه و توان مجموع آن‌ها است.

$$\large {\displaystyle a^b \times a^c = a^{( b + c)} }$$

• قرارگیری بی‌نهایت، چه در پایه و چه در توان، باعث می‌شود که عدد نامشخص باشد و بهتر است، حاصل ضرب اعداد با توان یا پایه بی‌نهایت را همان بی‌نهایت در نظر بگیریم. البته اگر به جای بی‌نهایت، منفی بی‌نهایت قرارگیرید، باید عدد حاصل را تقریبا برابر با صفر محسوب کرده و در عمل ضرب به کار ببریم.

$$\large {\displaystyle a^{ \infty} \times a^c = a^{ \infty} , \;\; a \neq 0}$$

$$\large {\displaystyle a^{- \infty} \times a^c = a^{ -\infty} = 0, \;\; a \neq 0 }$$

$$\large {\displaystyle {\infty}^b \times a^c = \infty^{( b + c)} = \infty , \;\; b + c \neq 0 }$$

با به خاطر سپردن قواعدی که در مورد ضرب اعداد توان دار گفتیم، می‌توانید بسیاری از محاسبات را به صورت نمادین انجام دهید و احتیاج به تقسیم و ضرب اعداد اعشاری نخواهید داشت. در نهایت جواب یا پاسخ‌های این گونه عملیات نیز براساس ساده کردن اعداد توان دار صورت خواهد گرفت.

خلاصه و جمع‌بندی

اعداد توان دار برای نمایش ساده‌تر اعداد بزرگ و کوچک به کار می‌رود. از طرفی شیوه محاسبه ضرب و تقسیم، حتی جمع و تفریق آن‌ها نیز با بقیه اعداد متفاوت است. در این متن به موضوع ضرب اعداد توان دار توجه کردیم و شیوه انجام این عمل ریاضی را برای این گونه اعداد بیان کردیم. همانطور که مشخص شد، ضرب کردن اعداد توان دار و ساده سازی نتیجه، در نمایش و انجام عملیات جبری روی چنین اعدادی، یک مفهوم پایه محسوب می‌شود. در نوشتارهای دیگری از مجله فرادرس به موضوعات مربوط به تقسیم اعداد توان دار و همچنین جمع و تفریق چنین اعدادی پرداخته‌ایم.