ضرایب لاگرانژ — به زبان ساده

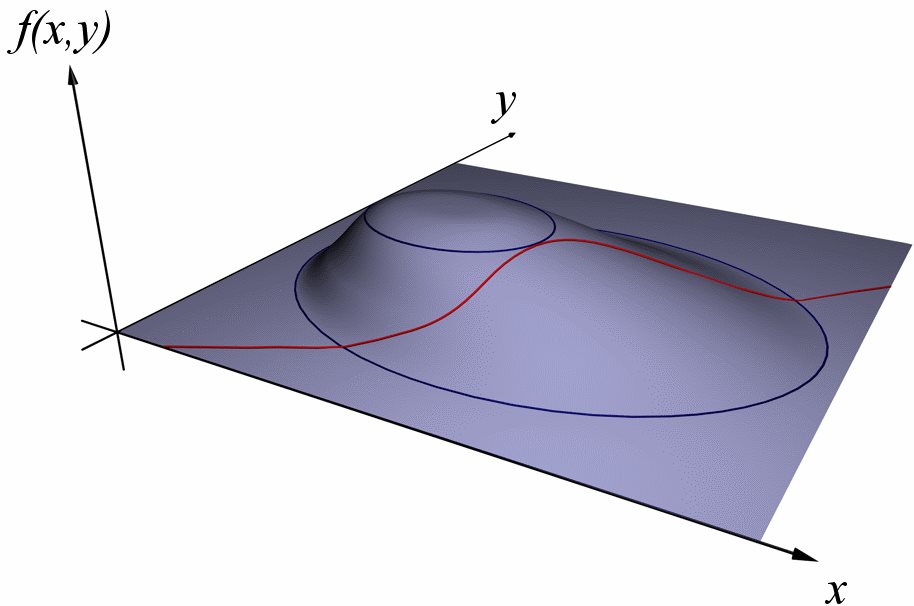
پیش‌تر در وبلاگ فرادرس مفاهیم مربوط به نحوه یافتن ماکزیمم و مینیمم یک تابع را توضیح دادیم. در این مطلب قصد داریم تا ماکزیمم یا مینیمم یک تابع را تحت یک قید خاص بدست آوریم. برای انجام این کار از روش ضرایب لاگرانژ استفاده می‌کنیم.

پیشنهاد می‌شود جهت درک بهتر این مطلب، مطالب دیورژانس، تابع چند متغیره و گرادیان مطالعه شوند.

ضرایب لاگرانژ

هدف ما یافتن ماکزیمم یا مینیمم تابع $$ f \left ( { x , y , z } \right) $$ تحت قید $$ g\left( {x,y,z} \right) = k $$ است. برای نمونه فرض کنید می‌خواهیم با فرض این‌که مساحت جانبی یک معکب مستطیل را داریم، بیشترین حجم ممکن را بدست آوریم.

فیلم آموزش ریاضیات مهندسی – حل سوالات کنکور ارشد و دکتری در فرادرس

کلیک کنید

برای بدست آوردن ماکزیمم یا مینیمم تابع $$ f \left ( { x , y , z } \right) $$ که تحت قید $$ g\left( {x,y,z} \right) = k $$ قرار گرفته باید مراحل زیر را انجام دهید:

1. دو سیستم معادله‌ای زیر را تشکیل دهید.

$$ \large \begin {align*} \nabla f \left( { x , y , z } \right ) & = \lambda \, \, \nabla g \left( { x , y , z } \right ) \\ g \left ( { x , y , z } \right ) & = k \end {align*} $$

2. مقادیر y ،x و z بدست آمده از قدم اول را در $$ f \left ( { x , y , z } \right) $$ قرار داده و ماکزیمم و مینیمم مقادیر f را بدست آورید.

در روابط بالا به $$ \lambda $$ ضریب لاگرانژ گفته می‌شود. شاید قدم‌های ارائه شده در بالا برای شما گیج کننده باشند، اما در ادامه مثال‌هایی ارائه شده که می‌تواند در درک موضوع بسیار کمک‌کننده باشد. توجه داشته باشید که دو رابطه ارائه شده در قدم اول، نشان دهنده ۴ معادله است. با باز کردن رابطه مربوط به گرادیان، داریم:

$$ \large \left \langle { { f _ x } , { f _ y } , { f _ z } } \right \rangle = \lambda \left \langle { { g_ x } , { g _ y } , { g _ z } } \right \rangle = \left \langle { \lambda { g _ x } , \lambda { g _ y } , \lambda { g _ z } } \right \rangle $$

برای برقراری رابطه فوق، تمامی مولفه‌های دو سمت رابطه، باید با یکدیگر مساوی باشند. بنابراین می‌توان گفت:

$$ \large { f _ x } = \lambda { g _ x } \hspace {0.25in} { f _ y } = \lambda { g _ y} \hspace {0.25in} { f _ z } = \lambda {g_z} $$

سه رابطه در بالا بدست آمد. این روابط به همراه رابطه $$ g \left ( { x , y , z } \right ) = c $$ ۴ معادله را تشکیل می‌دهند که با حل آن‌ها y ،x و z و $$ \lambda $$ بدست می‌آیند. توجه داشته باشید در حالتی که با تابعی دو متغیره کار می‌کنیم، تعداد مجهولات ۳ مورد خواهد بود.

جهت توضیح فیزیکی معادلات فوق، تابع $$ f \left ( { x , y } \right ) = 8 { x ^ 2 } - 2 y $$ را در نظر بگیرید. فرض کنید می‌خواهیم مقادیر ماکزیمم و مینیمم این تابع را در حالتی بدست آوریم که نقاط بدست آمده، روی دایره $$ { x ^ 2 } + { y ^ 2 } = 1 $$ قرار داشته باشند.

به منظور توضیح مفهوم سوال در ابتدا شکل زیر را در نظر بگیرید.

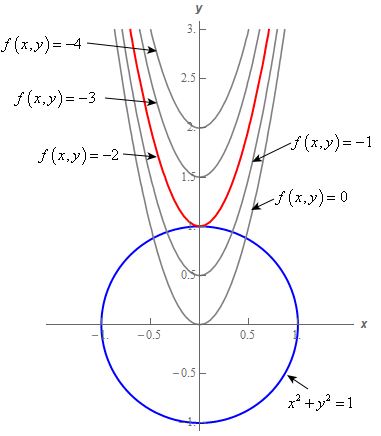
همان‌طور که می‌بینید تابع $$ f ( x , y ) =k $$ به ازای kهای مختلف ترسیم شده است. حال نقطه (x,y) باید به نحوی یافته شود که k بیشترین یا کمترین مقدار بوده و تابع $$ f ( x , y ) =k $$ با $$ { x ^ 2 } + { y ^ 2 } = 1 $$ برخورد داشته باشد. در تصویر فوق مینیمم مقدار k که البته با g نیز برخورد دارد، نموداری است که با رنگ قرمز نشان داده شده است. x,y معادل با نقطه برخورد، نشان دهنده مینیمم مقدار k است. البته از روی شکل می‌توان تشخیص داد که نقطه مذکور برابر با (0,1) است. با جایگذاری این مقدار در تابع f مقدار مینیمم آن برابر می‌شود با:

$$ \large f \left ( { x , y } \right ) = 8 { x ^ 2 } - 2 y \Rightarrow f ( 0 , 1 ) = -2 $$

مثال ۱

ابعاد جعبه‌ای با بیشترین حجم را با استفاده از روش ضرایب لاگرانژ بیابید. هم‌چنین فرض کنید مساحت جانبی آن نیز برابر با $$ 6 4 \ c m ^ 2 $$ است.

فیلم آموزش ریاضیات مهندسی پیشرفته در فرادرس

کلیک کنید

ما به دنبال بیشترین حجم هستیم. بنابراین هدف ماکزیمم کردن تابع زیر است.

$$ \large f \left ( { x , y , z } \right ) = x y z $$

از طرفی می‌دانیم که مساحت سطح جانبی مکعب برابر با عدد ثابت ۶۴ است. بنابراین مساحت همان قید بوده که می‌توان آن را به صورت زیر بیان کرد:

$$ \large 2 x y + 2 x z + 2 y z = 6 4 \hspace{0.5in} \Rightarrow \hspace {0.5in} x y + x z + y z = 3 2 $$

بنابراین تابع g نیز به صورت زیر است.

$$ \large g ( x , y , z ) = x y + x z + y z = 32 $$

تابع $$ f \left( { x ,y , z } \right ) = x y z $$ به خودی خود دارای ماکزیمم یا مینیمم نسبی نیست. در حقیقت با طی کردن مسیر g باید مقادیر x,y,z به نحوی تعیین شوند که مقدار f ماکزیمم شود. با نوشتن روابط $$ \large \nabla f \left( {x,y,z} \right) = \lambda \nabla g \left( {x,y,z} \right) $$ و $$\large g \left ( {x,y,z} \right) = k $$ داریم:

$$ \large \begin {equation} y z = \lambda \left ( { y + z } \right ) \hspace {0.75in} \left ( { { f _ x } = \lambda { g _ x } } \right ) \end {equation} $$
معادله ۱

$$ \large \begin {equation} x z = \lambda \left ( { x + z } \right ) \hspace {0.75in} \left ( { { f _ y } = \lambda { g _ y } } \right ) \end {equation} $$
معادله ۲

$$ \large \begin {equation} x y = \lambda \left ( { x + y } \right ) \hspace {0.75in} \left ( { { f _ z } = \lambda { g _ z } } \right ) \end {equation} $$
معادله ۳

$$ \large \begin {equation} x y + x z + y z = 3 2 \hspace {0.75in} \left ( { g \left ( { x , y , z } \right ) = 32 } \right ) \end {equation} $$
معادله ۴

راه‌های بسیاری به منظور حل معادلات فوق وجود دارد. در ابتدا معادله ۱ را در x، معادله ۲ را در y و معادله ۳ را در z ضرب می‌کنیم.

 $$ \large \begin {equation} x y z = \lambda x \left( { y + z } \right ) \end {equation} $$
معادله ۵

$$ \large \begin {equation} x y z = \lambda y \left ( { x + z } \right) \end {equation} $$
معادله ۶

$$ \large \begin {equation} x y z = \lambda z \left ( { x + y } \right ) \end {equation} $$
معادله ۷

با برابر قرار دادن معادله‌های ۵ و ۶ داریم:

$$ \large \begin {align*} \lambda x \left ( { y + z } \right ) & = \lambda y \left ( { x + z } \right ) \\ \lambda \left ( { x y + x z } \right ) - \lambda \left ( { y x + y z } \right ) &= 0 \\ \lambda \left ( { x z - y z } \right ) & = 0 \hspace {0.5in} \Rightarrow \hspace {0.5in} \lambda = 0 \, \, \, \, \, \,{ \mbox {or}} \, \, \, \, \, x z = y z \end {align*} $$

همان‌طور که محاسبه شد، دو حالت پیش می‌آید. حالت اول زمانی است که $$ \large \lambda = 0 $$ است. در این حالت با توجه به معادله ۱ مقادیر y یا z برابر با صفر بدست می‌آیند. این در حالی است که ابعاد جعبه نمی‌تواند صفر باشد. بنابراین حالت دوم را به صورت زیر در نظر می‌گیریم.

$$ \large x z = y z $$

از آنجایی که می‌دانیم مقدار که $$ \large z \ne 0 $$ است، بنابراین می‌توان آن را از طرفین رابطه فوق حذف کرد. در نتیجه داریم:

$$ \large x z = y z $$
معادله ۸

حال با برابر قرار دادن معادله‌های ۷ و ۶ داریم:

$$ \large \begin {align*} \lambda y \left ( { x + z } \right ) & = \lambda z \left ( { x + y } \right ) \\ \lambda \left ( { y x + y z - z x - z y } \right ) & = 0 \\ \lambda \left ( { y x - z x } \right ) & = 0\hspace {0.5in} \Rightarrow \hspace {0.5in} \lambda = 0 \, \, \, {\mbox{or}} \, \, \, \, y x = z x \end{align*} $$

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

همان‌طور که در بالا نیز توضیح داده شد، حالت $$ \large \lambda = 0 $$ پاسخ را به ما نمی‌دهد. بنابراین معادله زیر باید برقرار باشد.

$$ \large y x = z x $$

در این حالت نیز $$ \large x \ne 0 $$ است؛ لذا با حذف کردن آن از طرفین رابطه فوق، به عبارت زیر می‌رسیم.

$$ \large \begin {equation} z = y \end {equation} $$

در مرحله بعد معادله‌های ۸ و ۹ را در معادله ۴ قرار می‌دهیم. با انجام این کار y برابر با مقدار زیر بدست می‌آید.

$$ \large { y ^ 2 } + { y ^ 2 } + { y ^ 2 } = 3 { y ^ 2 } = 3 2 \hspace {0.5in} y = \pm \sqrt { \frac { { 3 2 } } { 3 } } = \pm \, 3 . 2 6 6 $$

از طرفی مقدار y نشان دهنده طول بوده و مقدار آن نمی‌تواند منفی باشد؛ لذا y=3.266 پاسخ درست محسوب شده و ابعاد مکعب به صورت زیر بدست می‌آید.

$$ \large x = y = z = \, 3 . 2 6 6 $$

توجه داشته باشید که هرگاه در روش ضرایب لاگرانژ یک پاسخ بدست می‌آید، باید مینیمم یا ماکزیمم بودن آن چک شود. بدین منظور در ابتدا مقدار حجم یا همان تابع f را به ازای متغیر‌های بدست آمده محاسبه می‌کنیم.

$$ \large V = f \left ( { \sqrt { \frac { { 3 2 } } { 2 } } ,\sqrt { \frac { { 3 2 } } { 2 } } , \sqrt { \frac { { 3 2 } } { 2} } } \right ) = { \left ( { \sqrt { \frac { { 3 2 } } { 2 } } } \right ) ^ 3 } = 3 4 .8 3 7 6 $$

حال برای چک کردن ماکزیمم یا مینیمم بودن مقدار حجم بدست آمده کافی است تا نقطه‌ای دیگر را روی قید g انتخاب کرده و به ازای آن حجم را بدست آورد. با مقایسه این مقدار با مقدار بدست آمده در بالا (مقدار بهینه) می‌توان ماکزیمم یا مینیمم بودن مقدار بهینه را تشخیص داد.

برای نمونه نقطه دلخواهی با x=y=1 را در نظر بگیرید. با جایگذاری این مقدار در تابع g داریم:

$$ \large 1 + z + z = 3 2 \hspace {0.25in} \to \hspace {0.25in} 2 z = 3 1 \hspace {0.25in} \to \hspace {0.25in} z = \frac { { 3 1 } } { 2 } $$

حجم مکعب به ازای این مختصات برابر است با:

$$ \large V = f \left ( { 1 , 1 , \frac { { 3 1 } }{ 2 } } \right ) = \frac { { 3 1 } } { 2 } = 1 5 . 5 < 34.8376 $$

همان‌طور که دیدید مقدار بدست آمده به ازای یک نقطه فرضی، کمتر از مقدار بهینه بود؛ لذا عدد بدست آمده نشان دهنده ماکزیمم حجم است. در مثال فوق دیدید که مقدار $$ \large \lambda $$ یا همان ضریب لاگرانژ بدست نیامد.

مثال ۲

ماکزیمم و مینیمم تابع $$ f \left ( { x , y } \right ) = 5 x - 3 y $$ را روی دیسک $$ { x ^ 2 } + { y ^ 2 } = 1 3 6 $$ با استفاده از روش ضرایب لاگرانژ بدست آورید.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

در ابتدا دستگاه معادلات را به صورت زیر تشکیل می‌دهیم.

$$ \large \begin {align*} 5 & = 2 \lambda x \\ - 3 & = 2 \lambda y \\ { x ^ 2 } + { y ^ 2 } & = 1 3 6 \end {align*} $$

همانند مثال ۱ در این مثال نیز مقدار λ نمی‌تواند صفر باشد. بنابراین با حل معادلات فوق، متغیر‌های x و y به صورت زیر بدست می‌آیند. با قرار دادن x و y در رابطه دیسک، به معادله‌ای بر حسب λ می‌رسیم.

$$ \large x = \frac { 5 } { { 2 \lambda } } \hspace {0.75in} y = - \frac { 3 } { { 2 \lambda } } $$

بنابراین ضرایب لاگرانژ برابرند با:

$$ \large { \lambda ^ 2 } = \frac { 1 } { { 1 6 } } \hspace {0.25in} \Rightarrow \hspace {0.25in} \, \, \, \, \, \lambda = \pm \frac { 1 } { 4 } $$

حال با بدست آمدن λ مقادیر x و y مربوط به ماکزیمم و مینیمم نیز قابل محاسبه است.

برای حالت $$ \large { \lambda } = - \frac { 1 } { 4 } $$:

$$ \large x = - 1 0 \hspace {0.75in} y = 6 $$

برای حالت $$ \large \large { \lambda } = \frac { 1 } { 4 } $$:

$$ \large x = 1 0 \hspace {0.75in} \hspace {0.25in} y = - 6 $$

بنابراین مقادیر ماکزیمم و مینیمم تابع f تحت قید g،‌ برابر با مقادیر زیر بدست می‌آیند.

$$ \large \begin{align*}f\left( { - 10,6} \right) & = - 68 & \hspace{0.25in} &{\mbox{Minimum at }}\left( { - 10,6} \right)\\ f\left( {10, - 6} \right) & = 68 & \hspace{0.5in} & {\mbox{Maximum at }}\left( {10, - 6} \right)\end{align*} $$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش ریاضی عمومی ۲
• آموزش ریاضیات عمومی ۱
• دیورژانس (Divergence) — به زبان ساده
• مشتق — به زبان ساده

^^