سرعت زاویه ای — به زبان ساده

در مطالب گذشته وبلاگ فرادرس روابط حاکم بر حرکت دایره‌ای را توضیح دادیم. اما در این مطلب قصد داریم تا مشخصا در مورد مفاهیم و روابط حاکم بر سرعت زاویه ای صحبت کنیم. البته به منظور درک بهتر پیشنهاد می‌شود مطالب بردار و اسکالر، قانون دست راست و ضرب خارجی را مطالعه فرمایید.

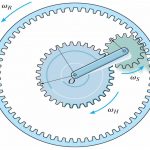
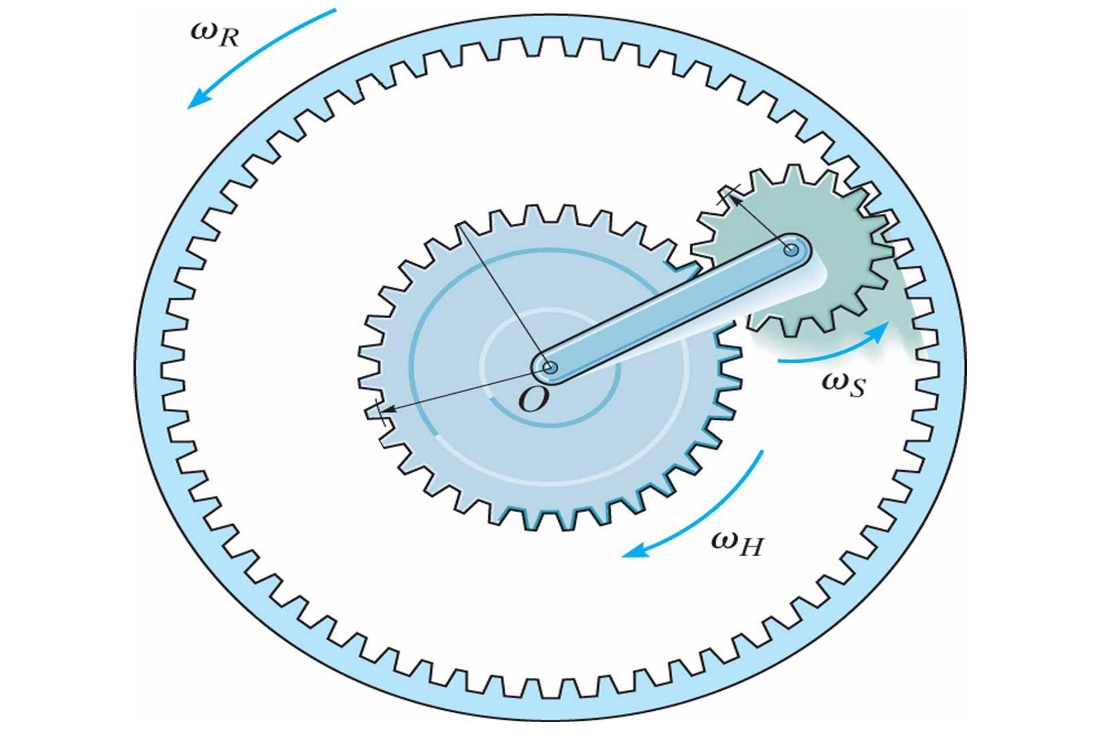
مقدمه

همان‌طور که احتمالا می‌دانید سرعت زاویه‌ای، نشان دهنده میزان زاویه‌ پیموده شده یک جسم یا ذره بر واحد زمان است. بنابراین سرعت زاویه‌ ای می‌تواند بر حسب رادیان بر زمان (ثانیه، دقیقه، ساعت و ...)، دور بر زمان یا درجه بر زمان بیان شود. توجه داشته باشید که سرعت زاویه‌ای، یک بردار بوده که می‌تواند جهت آن نیز با زمان تغییر کند. از این رو مشتق آن را نمی‌توان به راحتی و همچون یک تابع اسکالر بدست آورد.

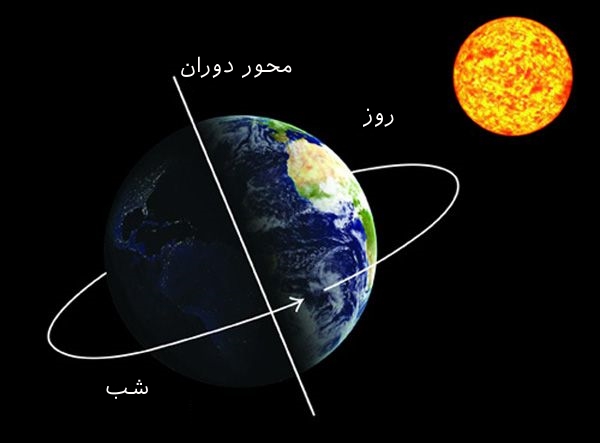
سرعت زاویه‌ای و سرعت خطی

پیش‌تر بیان کرده بودیم که برای حرکتی با سرعت خطی ثابت، اندازه سرعت زاویه‌ای برابر است با:

$$\large \omega = \frac{ \theta }{ t }$$

در رابطه فوق $$\large \theta$$ نشان دهنده سرعت زاویه‌ ای و $$t$$ نشان دهنده مدت زمانی است که حرکت دایره‌ای انجام شده است.

فیلم آموزش فیزیک پایه 1 – جامع و کاربردی در فرادرس

کلیک کنید

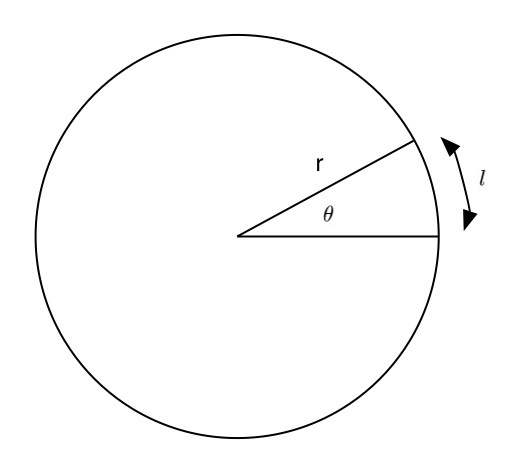
با توجه به شکل فوق فرض کنید متحرکی با سرعت زاویه‌ای روی دایره‌ای با سرعت زاویه‌ای ثابتِ $$\omega$$ در حال حرکت است. در این صورت اندازه زاویه طی شده بر حسب رادیان برابر است با:

$$\large \theta \text{ (in radians) } = \frac { l } { r }$$

از طرفی بدیهی است که سرعت خطی یک متحرک برابر است با:

$$\large v = \frac { l } { t }$$

رابطه فوق را می‌توان بر حسب $$\theta$$ به صورت زیر بیان کرد:

$$\large v = \frac { \theta r } { t }$$

بنابراین $$\theta$$ برابر است با:

$$\large \theta = \frac { v t } { r }$$

نهایتا رابطه بین $$\omega$$ و $$v$$ (رابطه بین سرعت خطی و سرعت زاویه‌ای) را می‌توان به صورت زیر بیان کرد:

$$\large \boxed { \omega = \frac { v t } { r } \cdot \frac { 1 } { t } \ \ \ , \ \ \ { \omega = \frac{ v }{ r } } }$$

جهت سرعت زاویه‌ای $$\large \overrightarrow { \omega }$$

فرض کنید ذره‌ای روی مسیری دایره‌ای شکل در حال حرکت است. هم‌چنین بردار این ذره در هر لحظه را با $$\overrightarrow { r }$$ نشان می‌دهیم. بدیهی است که جهت این بردار با گذشت زمان تغییر می‌کند. با فرض این‌که بردار سرعت در هر لحظه برابر با $$\overrightarrow { v }$$ باشد، در این صورت رابطه بین دو بردار سرعت زاویه‌ای و سرعت خطی برابر است با:

$$\boxed { \overrightarrow { \omega } = \frac { \overrightarrow { r } \times \overrightarrow { v } } { | \overrightarrow { r } | ^ { 2 } } }$$

در رابطه فوق $$\overrightarrow { r } \times \overrightarrow { v }$$ نشان دهنده ضرب خارجی دو بردار مکان و سرعت است. همان‌طور که در شکل زیر نیز نشان داده شده، بردار سرعت و مکان ذره به یکدیگر عمود هستند.

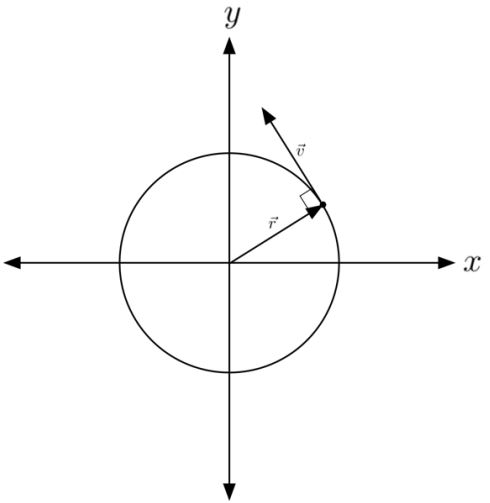
به منظور یافتن جهت بردار سرعت زاویه‌ای، کافی است از قانون دست راست استفاده کنید. در ابتدا شکل زیر را در نظر بگیرید.

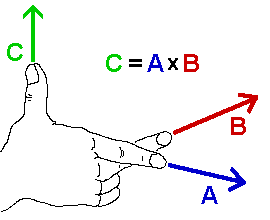
در شکل فوق اگر انگشت $$A$$ و $$B$$ به ترتیب نشان دهنده بردار سرعت و بردار مکان باشند، در این صورت جهت بردارِ حاصل ضرب خارجی، نشان دهنده جهت بردار $$\overrightarrow { \omega}$$ است. برای نمونه همان‌طور که در شکل زیر نیز مشاهده می‌شود، جهت بردار ذره‌ای که به صورت پادساعتگرد روی یک مسیر در حال حرکت است به سمت بیرون از صفحه است.

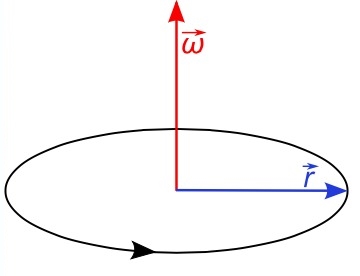
راه دیگر آن است جهت انگشتانتان را در جهت مسیر حرکت ذره خم کرده، در این صورت جهت بردار بدست خواهد آمد. در شکل زیر نحوه بدست آوردن جهت بردار سرعت زاویه‌ای نشان داده شده است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• مجموعه آموزش‌های دروس مهندسی مکانیک
• حرکت دایره‌ای — به زبان ساده
• ژیروسکوپ - از صفر تا صد
• تُندی و سرعت - به زبان ساده