زاویه مکمل چیست؟ – به زبان ساده + حل تمرین و مثال
زاویههای مکمل، زاویههایی هستند که جمعشان برابر با ۱۸۰ درجه میشود. این زاویهها، کاربردهای زیادی در دنیای واقعی و مسائل هندسی دارند. در این مقاله، به معرفی زاویه مکمل و محاسبات آنها به همراه حل چندین مثال متنوع میپردازیم. به علاوه، حضور زاویههای مکمل در شکلهای مختلف هندسی را نیز بررسی میکنیم.


زاویه ها چگونه تقسیم بندی می شوند ؟
زاویههای مختلف، معمولا بر اساس اندازه به انواع زاویههای تند، راست، باز، نیمصفحه، کاو (بازتاب) و تمامصفحه تقسیم میشوند. علاوه بر اندازه، رابطه بین دو زاویه نیز، از معیارهای مهم برای تقسیمبندی این شکلهای هندسی است. با توجه به این معیار، انواع زاویه عبارت هستند از:
- زاویه متمم
- زاویه مکمل
- زاویه مجاور
- زاویه متقابل به راس
- جفت خطی
- زاویه متبادل
- زاویه متناظر
از بین موارد بالا، عنوانها و تعریفهای زاویه متمم و زاویه مکمل، شباهت زیادی به یکدیگر دارند. این زاویهها، بر اساس حاصلجمع دو زاویه تشخیص داده میشوند. برای یادگیری بیشتر راجع به زاویهها و انواع آنها، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
زاویه مکمل چیست ؟
دو زاویهای که حاصلجمع آنها برابر با ۱۸۰ درجه است، با عنوان «زاویههای مکمل» (Supplementary Angles) شناخته میشوند.
به عنوان مثال، دو زاویه ۱۰۰ و ۸۰ درجه، دو زاویه ۱۳۰ و ۵۰ درجه و دو زاویه راست، با یکدیگر زاویه ۱۸۰ درجه میسازند. به همین دلیل، به این جفتزاویهها، زاویههای مکمل میگویند.
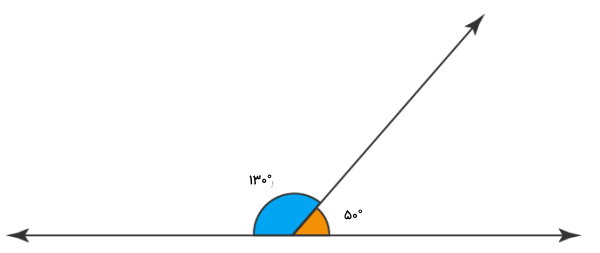
زاویههای مکمل میتوانند مانند تصویر بالا، دارای یک ضلع و یک راس مشترک بوده یا به عبارت دیگر، مجاور باشند. با این حال، اگر جمع دو زاویه جدا از هم، برابر با ۱۸۰ درجه شود، آن دو زاویه نیز، مکمل یکدیگر در نظر گرفته میشوند.
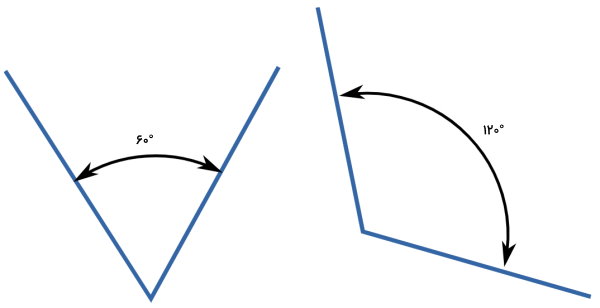
تفاوت زاویه مکمل و زاویه متمم چیست ؟
اگر جمع دو زاویه برابر با ۹۰ درجه باشد، به آنها، دو زاویه متمم میگویند. بنابراین، تفاوت زاویه متمم و مکمل، حاصلجمع آنها است. در صورت کنار هم قرار دادن دو زاویه مکمل، یک خط راست (زاویه نیمصفحه) ایجاد میشود. در طرف مقابل، با کنار هم گذاشتن دو زاویه متمم، یک زاویه راست یا دو خط عمود بر هم به وجود میآید.
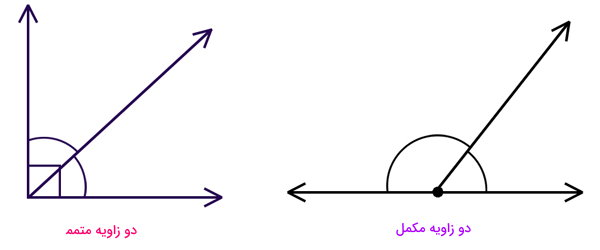
مثال ۱: محاسبه مکمل یک زاویه
مکمل زاویه ۴۵ درجه چند است؟
جمع مکمل یک زاویه با آن زاویه برابر با ۱۸۰ درجه میشود. رابطه بین زاویههای مکمل را میتوانیم به صورت زیر بنویسیم:
۱۸۰° = زاویه دوم + زاویه اول = جمع زاویههای مکمل
اندازه یکی از زاویهها را داریم. مقدار زاویه معلوم را درون رابطه بالا قرار میدهیم و آن را برای تعیین زاویه دوم حل میکنیم:
۱۸۰° = زاویه دوم + °۴۵
۴۵° – ۱۸۰° = زاویه دوم
۱۳۵° = زاویه دوم
در نتیجه، مکمل زاویه ۴۵ درجه برابر با ۱۳۵ درجه است.
مثال ۲: مکمل زاویه راست
مکمل زاویه راست را به دست بیاورید.
به زاویهای که اندازه آن برابر با ۹۰ درجه باشد، زاویه راست یا قائمه میگویند. مکمل زاویه راست، یک زاویه راست دیگر است؛ چراکه حاصلجمع ۹۰ با ۹۰ برابر با ۱۸۰ میشود:
۱۸۰° = ۹۰° + ۹۰°

مثال ۳: محاسبه مکمل یک زاویه از روی نسبت
نسبت یک زاویه با مکمل آن، برابر با یکسوم است. اندازه مکمل این زاویه را به دست بیاورید.
به منظور حل این مثال، یک زاویه با عنوان α و مکمل آن را با عنوان β در نظر میگیریم. جمع این دو زاویه برابر با ۱۸۰ درجه است:
از طرفی، نسبت α و β برابر با یکسوم است. این نسبت را به صورت زیر مینویسیم:
اکنون، نسبت بالا را بر حسب α بازنویسی میکنیم:
عبارت بالا را درون رابطه حاصلجمع دو زاویه قرار میدهیم:
با حل رابطه بالا، به اندازه مکمل زاویه α خواهیم رسید:
در نتیجه، مکمل زاویه مورد سوال برابر با ۱۳۵ درجه است.
مثال ۴: محاسبه متمم یک زاویه از روی مکمل آن
مکمل یک زاویه برابر با ۱۰۱ درجه است. آیا این زاویه متمم دارد؟ در صورت مثبت بودن جواب، اندازه متمم را حساب کنید.
اگر مکمل یک زاویه برابر با ۱۰۱ درجه باشد، اندازه آن زاویه برابر است با:
۱۸۰° = مکمل زاویه + زاویه
۱۸۰° = ۱۰۱° + زاویه
۱۰۱° - ۱۸۰° = زاویه
۷۹° = زاویه
اندازه زاویه مورد سوال، ۷۹ درجه است. به دلیل کوچکتر بودن زاویه ۷۹ درجه از زاویه ۹۰ درجه، این زاویه، متمم دارد. اندازه متمم زاویه ۷۹ درجه از رابطه زیر به دست میأید:
۹۰° = زاویه دوم + زاویه اول = جمع زاویههای متمم
۹۰° = متمم زاویه + زاویه
۹۰° = متمم زاویه + °۷۹
۷۹° - ۹۰° = متمم زاویه
۱۱° = متمم زاویه
بنابراین، متمم زاویه ۷۹ درجه برابر با ۱۱ درجه است.

مثال ۵: محاسبه مکمل یک زاویه از روی اختلاف اندازه
اختلاف دو زاویه مکمل برابر با ۱۴۶ درجه است. اندازه هر دو زاویه را حساب کنید.
میدانیم که جمع دو زاویه مکمل، برابر با ۱۸۰ درجه میشود:
از طرفی، با توجه به صورت سوال، اختلاف دو زاویه برابر با ۱۴۶ درجه است:
اکنون، دو معادله با دو مجهول داریم. اگر طرفین این دو معادله را با یکدیگر جمع کنیم، به رابطه زیر میرسیم:
جمع و تفریق رابطه به دست آمده را انجام میدهیم:
اندازه یکی از زاویهها برابر با ۱۶۳ است. از روی این زاویه میتوانیم اندازه زاویه دیگر را نیز محاسبه کنیم:
در نتیجه، اندازه زاویه دوم برابر با ۱۷ درجه است. دو زاویه ۱۷ و ۱۶۳ درجه، مکمل یکدیگر هستند و اختلافشان برابر با ۱۴۶ درجه است. برای آشنایی با نحوه اندازهگیری زاویهها، مطالعه مطالب زیر را پیشنهاد میکنیم:
زاویه های مکمل در مثلثات
یکی از کاربردهای زاویههای مکمل، بازنویسی روابط مثلثاتی به شکلهای دیگر است. برخی از ویژگیهای زاویههای مکمل در مثلثات عبارت هستند از:
- سینوس یک زاویه، با سینوس مکمل آن برابری میکند.
- کسینوس یک زاویه، با مقدار منفی کسینوس مکمل آن برابری میکند.
- تانژانت یک زاویه، با مقدار منفی تانژانت مکمل آن برابری میکند.
اگر α و β را دو زاویه مکمل در نظر بگیریم، میتوانیم شکل مثلثاتی عبارتهای بالا را به صورت زیر بنویسیم:
زاویه های مکمل در چند ضلعی ها
زاویههای مکمل در بسیاری از چندضلعیها قابل مشاهده هستند. در واقع، وجود این زاویهها، به عنوان خواص برخی از چندضلعیهای در نظر گرفته میشود.
زاویههای مکمل در متوازی الاضلاع
متوازیالاضلاع، یک نوع چهارضلعی است که ضلعهای روبهرویی آن با یکدیگر موازی هستند. زاویههای مجاور در این شکل هندسی، مکمل یکدیگر هستند.
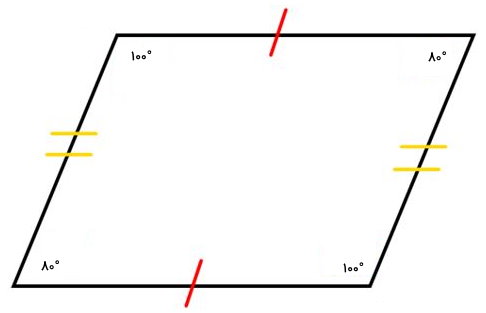
زاویههای مکمل در لوزی
لوزی، یک نوع چهارضلعی با ضلعهای برابر است. به دلیل موازی بودن ضلعهای لوزی، این شکل هندسی نیز به عنوان یک متوازیالاضلاع در نظر گرفته میشود. بنابراین، جمع دو زاویه داخلی مجاور لوزی، برابر با ۱۸۰ درجه است.

زاویههای مکمل در مربع و مستطیل
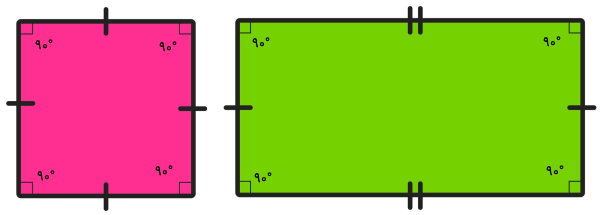
مربع و مستطیل، از دیگر انواع متوازیالاضلاع هستند. این شکلهای هندسی، چهار راس با زاویه ۹۰ درجه دارند. به همین دلیل، جمع هر دو زاویه داخلی مجاور یا غیر مجاور، برابر با ۱۸۰ درجه میشود. در واقع، هر دو زاویه داخلی مربع و مستطیل، مکمل یکدیگر هستند.
زاویههای مکمل در ذوزنقه
ذوزنقه، یکی دیگر از انواع چهارضلعیها است که میتوان زاویههای مکمل را در آن دید. این شکل، از دو ضلع موازی و دو ضلع غیرموازی تشکیل میشود. به ضلعهای موازی ذوزنقه، قاعده و به ضلعهای غیرموازی آن، ساق میگویند. زاویههای داخلی مجاور به ساق ذوزنقه، مکمل یکدیگرند.
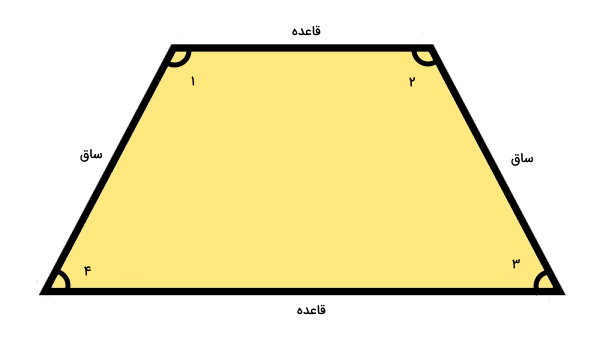
در تصویر بالا، زاویههای ۲ و ۳ و زاویههای ۱ و ۴، مکمل هستند. اثبات مکمل بودن این زاویهها با استفاده از قضیه خطوط موازی و جفتزاویهها انجام میگیرد.
زاویههای مکمل در مثلث و دیگر چند ضلعی ها
مثلثها، از سه ضلع و سه راس تشکیل میشوند. مجموع زوایای داخلی مثلث، همواره برابر با ۱۸۰ درجه است. بنابراین، به دلیل وجود سه زاویه داخلی، این شکل نمیتواند دو زاویه مکمل داشته باشد. با این وجود، امکان مشاهده زاویههای مکمل در تمام چندضلعیها، وجود دارد. به این منظور، کافی است یکی از ضلعهای هر راس را امتداد دهید.
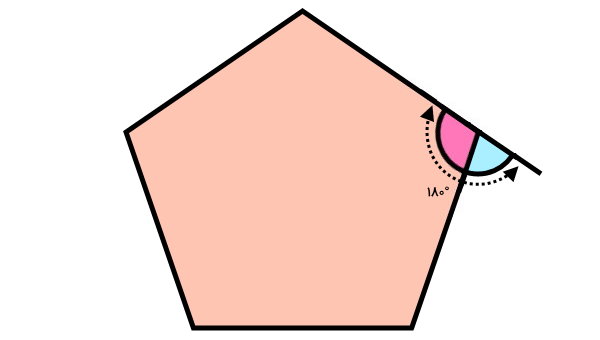
با امتداد یک ضلع چندضلعی، زاویه دیگری به وجود میآید که با عنوان زاویه خارجی شناخته میشود. تصویر بالا، یکی از زاویههای داخلی و خارجی در یک پنجضلعی منتظم را نمایش میدهد. زاویه داخلی (صورتی) و زاویه خارجی (آبی)، دو زاویه مکمل را تشکیل میدهند. این ویژگی، در تمام چندضلعیها صادق است.
زاویه های مکمل در خطوط متقاطع
هنگامی که دو یا چند خط با یکدیگر برخورد میکنند، در محل تقاطعشان، چندین زاویه به وجود میآید. هر دو زاویه خطوط متقاطع، با عنوان زاویههای متقاطع یا جفتزاویه شناخته میشوند.
تصویر زیر، نمونهای از این زاویهها را نمایش میدهد.
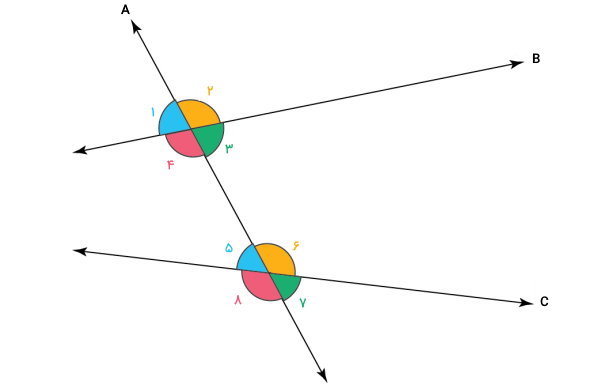
به زاویههایی که یک راس و یک ضلع مشترک دارند، زاویههای مجاور میگویند. زاویههای مجاور در شکل بالا عبارت هستند از:
- زاویههای ۱ و ۲
- زاویههای ۲ و ۳
- زاویههای ۳ و ۴
- زاویههای ۵ و ۶
- زاویههای ۶ و ۷
- زاویههای ۷ و ۸
اگر به ضلعهای غیر مشترک این زاویهها توجه کنید، مشاهده خواهید کرد که این ضلعها با یکدیگر یک خط راست یا بهاصطلاح یک زاویه نیمصفحه میسازند. به عبارت دیگر، جمع زاویههای مجاور در خطوط متقاطع، برابر با ۱۸۰ درجه است. این زاویهها، مکمل یکدیگرند.
مثال ۶: تعیین اندازه زاویههای دو خط متقاطع
دو خط متقاطع زیر را در نظر بگیرید. اگر اندازه زاویه «الف» در محل تقاطع این دو خط برابر با ۳۲ درجه باشد، اندازه سه زاویه دیگر چقدر میشود؟
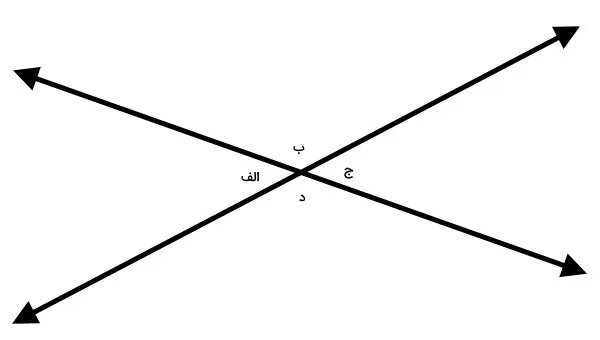
میدانیم که در خطوط متقاطع، زاویههای مجاور، مکمل یکدیگر هستند. بنابراین، برای زاویه «ب» داریم:
۱۸۰° = زاویه ب + زاویه الف
۱۸۰° = زاویه ب + °۳۲
۳۲° - ۱۸۰° = زاویه ب
۱۴۸° = زاویه ب
زاویه «ب» با زاویه «ج» مجاور است. از اینرو، رابطه بین این دو زاویه نیز به صورت زیر نوشته میشود:
۱۸۰° = زاویه ج + زاویه ب
۱۸۰° = زاویه ج + °۱۴۸
۱۴۸° - ۱۸۰° = زاویه ج
۳۲° = زاویه ج
زاویه «ج» و زاویه «د» نیز دو زاویه مکمل میسازند:
۱۸۰° = زاویه د + زاویه ج
۱۸۰° = زاویه د + °۳۲
۳۲° - ۱۸۰° = زاویه د
۱۴۸° = زاویه د
به این ترتیب، اندازه تمام زاویههای خط را محاسبه کردیم. اگر به اندازه این زاویهها دقت کرده باشید، احتمالا متوجه شدهاید که زاویههای مقابل یکدیگر در خطهای متقاطع، هماندازه هستند. این زاویهها با عنوان، زاویههای متقابل به راس شناخته میشوند.
سوالات متداول در رابطه با زاویه های مکمل
در این بخش، به برخی از سوالات متداول در رابطه با زاویههای مکمل، بهطور خلاصه پاسخ میدهیم.
زاویه مکمل یعنی چه؟
زاویه مکمل، یعنی زاویهای که جمعش با یک زاویه دیگر برابر با ۱۸۰ درجه شود.
اندازه زاویه مکمل چقدر است ؟
اندازه دو زاویه مکمل ۱۸۰ درجه است.
تفاوت زاویه مکمل و زاویه متمم در چیست؟
مجموع زاویههای متمم، برابر با ۹۰ درجه و کمتر از مجموع زاویههای مکمل (۱۸۰ درجه) است.
ذوزنقه چند زاویه مکمل دارد ؟
هر ذوزنقه، دو جفت زاویه مکمل دارد (زاویههای مجاور ساق).
مکمل زاویه ۲۰ درجه چند است ؟
۱۶۰ درجه.
مکمل زاویه ۳۰ درجه چند است ؟
۶۰ درجه.
مکمل زاویه ۵۰ درجه چند است ؟
۱۳۰ درجه.
مکمل زاویه ۷۰ درجه چند است ؟
۱۱۰ درجه.
مکمل زاویه قائمه چند است ؟
مکمل زاویه قائمه، یک زاویه ۹۰ درجه است.
زاویه های داخلی کدام شکل مکمل یکدیگر هستند ؟
زاویه های داخلی و مجاور متوازی الاضلاع مکمل یکدیگر هستند.
آزمون زاویه مکمل
۱. کدام تعریف، به طور دقیق مفهوم زاویههای مکمل را بیان میکند؟
دو زاویه که جمع آنها ۱۸۰ درجه باشد مکمل هستند.
دو زاویه که یک ضلع مشترک دارند مکمل اند.
دو زاویه که کنار هم قرار میگیرند مکمل نام دارند.
دو زاویه که جمع آنها ۹۰ درجه باشد مکمل هستند.
تعریف درست زاویههای مکمل این است که وقتی جمع دو زاویه دقیقا برابر با ۱۸۰ درجه باشد آنها مکمل یکدیگر هستند.
۲. در یک چهارضلعی، کدام ویژگی موجب مکمل بودن دو زاویه مجاور میشود؟
دو زاویه روبرو با هم برابر باشند.
همه زوایا به یک اندازه باشند.
هر زاویه کمتر از ۹۰ درجه باشد.
مجموع دو زاویه مجاور برابر با ۱۸۰ درجه شود.
هنگامی که مجموع زاویههای مجاور در یک چهارضلعی برابر با ۱۸۰ درجه باشد، آن زوایا مکمل نامیده میشوند.
۳. تفاوت اصلی میان زاویه مکمل و زاویه متمم در چیست و هرکدام باعث تشکیل چه نوع زاویه یا شکل هندسی میشوند؟
زاویه مکمل مجموعا ۱۸۰ درجه دارد و کنار هم یک خط راست میسازد، زاویه متمم مجموعا ۹۰ درجه دارد و یک زاویه قائم میسازد.
زاویه مکمل تشکیل زاویه قائم میدهد و در مثلث دیده میشود، زاویه متمم همیشه در مربعها پیدا میشود.
زاویه مکمل و زاویه متمم هر دو همیشه جمعشان ۱۲۰ درجه است و کنار هم یک زاویه باز درست میکنند.
زاویه مکمل مجموعا ۹۰ درجه دارد و کنار هم یک زاویه حاده میسازد، زاویه متمم مجموعا ۱۸۰ درجه دارد و یک ذوزنقه میسازد.
تفاوت اصلی این است که مجموع دو زاویه مکمل برابر با ۱۸۰ درجه است و کنار هم که قرار بگیرند یک خط راست یا زاویه نیمصفحه ایجاد میکنند، اما دو زاویه متمم مجموعشان ۹۰ درجه است و در کنار هم زاویه قائم یا دو خط عمود به وجود میآورند.
۴. در محل تقاطع دو خط، چگونه میتوان با استفاده از رابطه مکمل بودن زاویههای مجاور، مجموع زاویههای تشکیلشده را به دست آورد؟
تمام زاویههای تشکیلشده همگی با هم برابرند و مجموعشان ۲۷۰ درجه است.
جمع هر دو زاویه مجاور برابر با ۱۸۰ درجه است و مجموع کل زاویهها ۳۶۰ درجه میشود.
فقط یکی از زاویههای مجاور مکمل یکدیگرند و مجموع کل ۱۸۰ درجه است.
زاویههای مجاور جمعا کمتر از ۱۸۰ درجه دارند و مجموع کلی ۹۰ درجه است.
وقتی دو خط یکدیگر را قطع میکنند، هر دو زاویه مجاور در محل تقاطع مکملاند و جمعشان ۱۸۰ درجه میشود. در این حالت، چهار زاویه ایجاد میگردد که مجموع کل زوایا «۳۶۰ درجه» است، زیرا هر جفت زاویه مجاور مکمل یکدیگر بوده و مجموع همه زاویهها باید دور یک نقطه را پوشش دهد.
۵. برای یافتن مقدار زاویه مکمل یک زاویه داده شده در هندسه، کدام روش درست است؟
اندازه زاویه داده شده را از ۱۸۰ درجه کم میکنیم.
تفاوت زاویه داده شده با ۹۰ درجه را به دست میآوریم.
مجموع زاویه داده شده را با ۱۸۰ درجه جمع میکنیم.
زاویه داده شده را بر ۲ تقسیم میکنیم.
برای پیدا کردن اندازه زاویه مکمل، باید «اندازه زاویه داده شده را از ۱۸۰ درجه کم کنیم»؛ چون تعریف زاویه مکمل این است که مجموع دو زاویه برابر با ۱۸۰ درجه باشد. بنابراین اگر یکی از زوایا معلوم باشد، با کم کردن آن عدد از ۱۸۰ درجه مقدار زاویه دیگر را به دست میآوریم.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «زاویه ها و انواع آن ها – هر آنجه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- زاویه چیست؟ — تعریف، انواع و اندازه گیری
- انواع زاویه چیست ؟ — معرفی تمام زاویه ها — به زبان ساده
- راس زاویه چیست ؟ — به زبان ساده + حل مثال تصویری
- زاویه حاده چیست ؟ — به زبان ساده + حل مثال های متنوع تصویری
- زاویه باز چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه قائمه چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه مکمل چیست ؟ — به زبان ساده + حل تمرین و مثال(همین مطلب)
- زاویه متمم چیست ؟ — به زبان ساده
- زاویه متقابل به راس چیست ؟ — به زبان ساده + حل تمرین و مثال
- زاویه های مکمل و متمم در هندسه — به زبان ساده
- زاویه نیمصفحه و تعریف آن در هندسه — به زبان ساده
- زاویه محاطی چیست ؟ — اثبات قضیه + حل تمرین و مثال های متنوع
- نیمساز چیست ؟ — به زبان ساده
- اندازه گیری زاویه با نقاله — به زبان ساده + مثال های تصویری
- اندازه گیری زاویه با گونیا — به زبان ساده + مثال های تصویری












