روش کرامر – از صفر تا صد

در آموزش‌‌های قبلی مجله فرادرس، با چگونگی حل دستگاه معادلات دو مجهول و سه مجهول به روش‌‌های مختلف از جمله روش جانشینی، جمع، حذف گوسی و استفاده از وارون یک ماتریس آشنا شدیم. به کار بردن برخی از این روش‌‌ها نسبت به سایر آن‌ها آسان‌‌تر و در شرایط خاص مناسب‌‌تر است. در این آموزش، روش دیگری را برای حل دستگاه معادلات خطی معرفی می‌‌کنیم که روش کرامر یا قاعده کرامر (Cramer's Rule) نام دارد.

محاسبه دترمینان ماتریس ۲×۲

دترمینان یک عدد حقیقی است که در ریاضیات بسیار مورد استفاده قرار می‌‌گیرد، زیرا کاربردهای گوناگونی همچون محاسبه مساحت، حجم و سایر کمیت‌‌ها دارد. در اینجا به این دلیل از دترمینان‌‌ها استفاده می‌‌کنیم که وارون‌‌پذیری ماتریس (ماتریس مربعی) و در نتیجه جواب داشتن یا نداشتن دستگاه معادلات مشخص شود.

یکی از کاربردهای جالب دیگر دترمینان، استفاده از آن‌ها در رمزنگاری است. پیام‌‌ها و سیگنال‌‌های امن گاهی اوقات به صورت یک ماتریس، رمزی (رمزی شده) ارسال می‌‌شوند. داده‌‌ها فقط می‌‌توانند با یک ماتریس وارون‌‌پذیر و دترمینان آن رمزگشایی شوند. محاسبه دترمینان یک ماتریس الگوی خاصی دارد که در این بخش به طور خلاصه آن را بیان می‌‌کنیم.

دترمینان یک ماتریس 2 در 2 مانندِ

$$\large A = \begin {bmatrix} a & b \\ c & d \end {bmatrix}$$

به این صورت تعریف می‌‌شود:

دترمینان را می‌‌توان به چند صورت نشان داد: از جمله $$\text{det}(A)$$ و جابه‌جایی براکت‌‌های ماتریس با خطوط راست، یعنی $$|A|$$.

مثال 1

دترمینان ماتریس زیر را به دست آورید.

$$\large A = \begin {bmatrix} 5 & 2 \\ − 6 & 3 \end {bmatrix}$$

حل:

$$\large \begin {align*} \det ( A ) & = \begin {vmatrix} 5 & 2 \\ - 6 & 3 \end {vmatrix} \\ & = 5 ( 3 ) - ( - 6 ) ( 2 ) \\ & = 27 \end {align*}$$

حل دستگاه دو معادله دو مجهول با استفاده از روش کرامر

در اینجا برای حل دستگاه معادلات، روشی را معرفی می‌‌کنیم که در آن از دترمینان استفاده می‌‌شود. این روش که به عنوان روش کرامر شناخته می‌‌شود، در سال 1750 توسط ریاضی دان سوئیسی، گابریل کرامر (Gabriel Cramer) معرفی شد. روش کرامر یک روش مناسب و کارآمد برای به دست آوردن جواب دستگاه معادلات با تعداد دلخواهی مجهول است، به شرطی که به همان تعداد مجهول، معادله داشته باشیم.

استفاده از روش کرامر برای حل دستگاه معادلات، در صورت وجود، جواب یکتایی را به ما می‌‌دهد. اما اگر دستگاه جواب نداشته باشد یا بیشمار جواب داشته باشد، با دترمینان صفر نشان داده خواهد شد. برای اینکه متوجه شویم دستگاه ناسازگار است یا وابسته، باید از روش دیگری مانند روش حذفی استفاده کنیم.

برای درک روش کرامر، به دقت نگاه کنید که چگونه دستگاه معادلات خطی را با استفاده از عمل‌‌های سطری اصلی حل می‌‌کنیم. یک دستگاه دو معادله دو مجهول را در نظر بگیرید:

$$\large \begin {align} a _ 1 x + b _ 1 y & = c _ 1 \;\;\;\;\; ( 1 ) \\ a _ 2 x + b _ 2 y & = c _ 2 \;\;\;\;\; ( 2 ) \end{align}$$

با استفاده از عمل‌‌های سطری یک متغیر را حذف و برای متغیر دیگر معادله را حل می‌‌کنیم. می‌‌خواهیم متغیر $$x$$ را به دست آوریم. اگر معادله (۲) را در منفی ضریب $$y$$ در معادله (۱) و معادله (۱) را در ضریب $$y$$ در معادله (۲) ضرب کرده، سپس این دو معادله را با هم جمع کنیم، متغیر $$y$$ حذف خواهد شد.

$$\large \begin {align*} & b _ 2 a _ 1 x + b _ 2 b _ 1 y = b _ 2 c _ 1 & \text {Multiply } R _ 1 \text { by } b _ 2 \\ -& \underline { b _ 1 a _ 2 x − b _ 1 b _ 2 y = − b _ 1 c _ 2 } & \text {Multiply } R _ 2 \text { by } − b _ 1 \\ & b _ 2 a_ 1 x − b _ 1 a _ 2 x =b _ 2 c _ 1 − b _ 1 c _ 2 \end {align*}$$

اکنون جواب $$x$$ را به دست می‌‌آوریم:

$$\large \begin {align*} b _ 2 a _ 1 x − b _ 1 a _ 2 x & = b _ 2 c _ 1 − b _ 1 c _ 2 \\ x ( b _ 2 a _ 1 − b _ 1 a _ 2 ) & = b _ 2 c _ 1 − b _ 1 c _ 2 \\ x & = \dfrac { b _2 c _ 1 − b _ 1 c _ 2} { b _ 2 a _ 1 − b_ 1a _ 2 } = \dfrac { \begin {bmatrix} c _ 1 & b _ 1 \\ c _ 2 & b _ 2 \end {bmatrix}}{ \begin {bmatrix} a _ 1 & b _ 1 \\ a _ 2 & b _ 2 \end {bmatrix} } \end {align*}$$

به طور مشابه، برای به دست آوردن $$y$$، متغیر $$x$$ را حذف می‌‌کنیم:

$$\large \begin {align*} & a _ 2 a _ 1 x + a _ 2 b _ 1 y = a _ 2 c _ 1 & \text {Multiply } R _ 1 \text { by } a _ 2 \\ - & \underline { a _ 1 a _ 2 x − a _ 1 b _ 2 y = − a _ 1 c _ 2 } & \text {Multiply } R _ 2 \text { by } − a _ 1 \\ & a _ 2 b _1 y − a _ 1 b _ 2 y = a _ 2 c _ 1 − a _ 1 c _ 2 \end {align*}$$

در نتیجه خواهیم داشت:

$$\large \begin {align*} a _ 2 b _ 1 y − a _ 1 b _ 2 y & = a _ 2 c _ 1 − a _ 1 c _ 2 \\ y ( a _ 2 b _1 − a _ 1 b _ 2 ) & = a _ 2 c _ 1 − a _ 1 c _ 2 \\ y & = \dfrac { a _ 2 c _ 1 − a _ 1 c _ 2 }{ a _ 2 b _ 1 − a _ 1 b _ 2 } = \dfrac { a _ 1 c _ 2 − a _ 2 c _ 1 }{ a _ 1 b _ 2 − a _ 2 b _ 1 } = \dfrac { \begin {bmatrix} a _ 1 & c _ 1 \\ a _ 2 & c _ 2 \end {bmatrix} }{ \begin {bmatrix} a _ 1 & b _ 1 \\ a _ 2 & b _ 2 \end {bmatrix}} \end {align*}$$

توجه داشته باشید که مخرج $$x$$ و $$y$$ دترمینان ماتریس ضرایب است.

می‌‌توانیم از این فرمول‌‌ها برای به دست آوردن $$x$$ و $$y$$ استفاده کنیم، اما در روش کرامر نمادگذاری به صورت زیر است:

• $$D$$: دترمینان ماتریس ضرایب
• $$D_x$$: دترمینان صورت کسر در جواب $$x$$

$$\large x = \dfrac { D _ x } { D } \;\;\;\;\; (3)$$

• $$D_y$$: دترمینان صورت کسر در جواب $$y$$

$$\large y = \dfrac { D _ y } { D } \;\;\;\;\; ( 4 )$$

نکته کلیدی روش کرامر، جابه‌جایی ستون متغیر مورد نظر با ستون ثابت‌‌ها و محاسبه دترمینان‌‌ها است. پس می‌‌توان $$x$$ و $$y$$ را با خارج قسمت دو دترمینان بیان کرد.

بنابراین، روش کرامر روشی است که برای حل دستگاه معادلاتی به کار می‌‌رود که دارای تعداد یکسانی معادله و مجهول هستند. یک دستگاه دو معادله و دو مجهول خطی را به صورت زیر در نظر بگیرید:

$$\large \begin {align*} a _ 1 x + b _ 1 y & = c _ 1 \\ a _ 2 x + b _ 2 y & = c _ 2 \end {align*}$$

جواب این معادلات با استفاده از روش کرامر به شکل زیر خواهد بود:

$$\large \begin {align} x & = \dfrac { D _ x } { D } = \dfrac { \begin {bmatrix} c _ 1 & b _ 1 \\ c _ 2 & b _ 2 \end {bmatrix}}{ \begin {bmatrix} a _ 1 & b _ 1 \\ a _ 2 & b _ 2 \end {bmatrix}} \; , D \neq 0 \;\;\;\;\; (5) \\ y & = \dfrac { D _ y } { D } = \dfrac { \begin {bmatrix} a _ 1 & c _ 1 \\ a _ 2 & c _ 2 \end {bmatrix} }{ \begin {bmatrix} a _ 1 & b _ 1 \\ a _ 2 & b _ 2 \end {bmatrix} } \; , D \neq 0 \;\;\;\;\; (6)\end {align}$$

اگر بخواهیم جواب $$x$$ را به دست آوریم، ستون $$x$$ را با ستون ثابت‌‌ها جابه‌جا می‌‌کنیم و در صورتی که بخواهیم جواب $$y$$ را به دست آوریم، ستون $$y$$ را با ستون ثابت‌‌ها جایگزین می‌‌کنیم.

مثال 2

دستگاه دو معادله و دو مجهول زیر را با استفاده از روش کرامر حل کنید.

$$\large \begin {align*} 1 2 x + 3 y & = 1 5 \\ 2 x - 3 y & = 1 3 \end {align*}$$

حل: با استفاده از روابط بالا مقادیر $$x$$ و $$y$$ به صورت زیر خواهند بود:

$$\large \begin {align*} x & = \dfrac { D _ x } { D } \\ & = \dfrac { \begin {bmatrix} 1 5 & 3 \\ 1 3 & - 3 \end {bmatrix}}{ \begin {bmatrix} 1 2 & 3 \\ 2 & - 3 \end {bmatrix} } \\ & = \dfrac { - 4 5 - 3 9 } { - 3 6 - 6 } \\ & = \dfrac { - 8 4 } { - 4 2 } \\ & = 2 \end {align*}$$

$$\large \begin {align*} y & = \dfrac { D _ y } { D } \\ & = \dfrac { \begin {bmatrix} 1 2 & 1 5 \\ 2 & 1 3 \end {bmatrix}}{ \begin {bmatrix} 1 2 & 3 \\ 2 & - 3 \end {bmatrix} } \\ & = \dfrac { 1 5 6 - 3 0 } { - 3 6 - 6 } \\ & = - \dfrac { 1 2 6 } { 4 2 } \\ & = - 3 \end {align*}$$

بنابراین، جواب این معادلات برابر با $$(2,−3)$$ است.

محاسبه دترمینان ماتریس 3×3

به دست آوردن دترمینان ماتریس 3 در 3 نسبت به ماتریس 2 در 2 پیچیده‌‌تر است. یک روش برای محاسبه دترمینان ماتریس 3 در 3 افزودن ماتریس 3 در 3 به دو ستون اول آن است. در این روش که یک ماتریس 5×3 به ما می‌‌دهد، مجموع حاصلضرب درایه‌‌های هر سه قطر را در جهت پایین (بالا سمت چپ به طرف پایین سمت راست) محاسبه کرده و مجموع حاصلضرب درایه‌‌های هر سه قطر در جهت بالا (پایین سمت چپ به طرف بالا سمت راست) را از آن کم می‌‌کنیم. برای درک بهتر این روش، یک مثال حل می‌‌کنیم.

می‌خواهیم دترمینان ماتریس زیر را به دست آوریم:

$$\large A = \begin {bmatrix} a _ 1 & b _ 1 & c _ 1 \\ a _ 2 & b _ 2 & c _ 2 \\ a _ 3 & b _ 3 & c _ 3 \end {bmatrix}$$

۱. ماتریس $$A$$ را به دو ستون اول آن اضافه می‌‌کنیم:

$$\large \det ( A ) = \left | \begin {array} {ccc|cc} a _ 1 & b _ 1 & c _ 1 & a _ 1 & b _1 \\ a _ 2 & b _ 2 & c _ 2 & a _ 2 &b _ 2 \\ a _ 3 & b _ 3 & c _ 3 &a _ 3 & b _ 3 \end {array} \right|$$

۲. از بالا سمت چپ به طرف پایین سمت راست، درایه‌‌های قطر اول، دوم و سوم را جداگانه در جهت پایین ضرب کرده و حاصل آن‌ها را با هم جمع می‌‌کنیم.

۳. از پایین سمت چپ به طرف بالا سمت راست، درایه‌‌های قطر اول، دوم و سوم را جداگانه در جهت بالا ضرب کرده و حاصل آن‌ها را از جواب به دست آمده در مرحله 2 کم می‌‌کنیم.

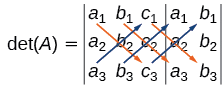
عبارت جبری آن به صورت زیر خواهد بود:

$$\large | A | = a _ 1 b _ 2 c _ 3 + b_ 1 c _2 a _ 3 + c _ 1 a _ 2b _ 3 − a_ 3 b _ 2 c _ 1 − b _ 3 c _ 2a _ 1 −c _ 3a _ 2 b _ 1$$

مثال 3

دترمینان ماتریس زیر را بیابید.

$$\large A = \begin {bmatrix} 0 & 2 & 1 \\ 3& − 1 & 1 \\ 4 &0 & 1 \end {bmatrix}$$

حل: ماتریس را به دو ستون اول آن اضافه می‌‌کنیم و سپس، روش فوق را به کار می‌‌گیریم:

$$\large \begin {align*} | A | & = \left | \begin {array}{ccc|cc} 0 & 2 & 1 & 0 & 2 \\ 3 & - 1 & 1 & 3 & - 1 \\ 4 & 0 & 1 & 4 & 0 \end {array} \right| \\ & = 0 ( − 1 ) ( 1 ) + 2 ( 1 ) ( 4 ) + 1 ( 3 )( 0 ) − 4 ( − 1 ) ( 1 ) − 0 ( 1 ) ( 0 ) − 1 ( 3 ) ( 2 ) \\ & = 0 + 8 + 0 + 4 − 0− 6 \\ & = 6 \end {align*}$$

حل دستگاه سه معادله و سه مجهول با استفاده از روش کرامر

اکنون که می‌‌توانیم دترمینان ماتریس 3×3 را محاسبه کنیم، می‌‌توانیم برای حل دستگاه سه معادله و سه مجهول، روش کرامر را به کار ببریم. روش کرامر برای ماتریس 3×3 الگویی مشابه با ماتریس‌‌های 2×2 دارد. از آنجایی که مرتبه ماتریس در اینجا افزایش یافته است، محاسبات بیشتری لازم خواهد بود.

هنگامی که دترمینان به دست آمده برابر با صفر است، با استفاده از روش کرامر نمی‌‌توان تعیین کرد که دستگاه معادلات جواب ندارد یا بیشمار جواب دارد. برای پی بردن به این موضوع باید روش حذفی را روی دستگاه معادلات انجام دهیم.

دستگاه معادلات زیر را در نظر بگیرید:

$$\large \begin {align} a _ 1 x + b _ 1 y + c _ 1 z & = \color {blue} d _ 1 \;\;\;\;\; (7)\\ a _ 2 x + b _ 2 y + c _2 z & = \color {blue} d _ 2 \;\;\;\;\; (8) \\ a _ 3 x + b _ 3 y + c _ 3 z & = \color {blue} d _ 3 \;\;\;\;\; (9) \end {align}$$

$$\large x = \dfrac { D _ x } { D } , \; y = \dfrac { D _ y } { D } , \; z = \dfrac { D _ z } { D } , \; D \neq 0$$

که در آن:

$$\large D = \begin {vmatrix} a _ 1 & b _ 1 & c _ 1 \\ a _ 2 & b _ 2 & c _ 2 \\ a _ 3 & b _ 3 & c _ 3 \end {vmatrix}\; ,\; D _ x = \begin {vmatrix} \color {blue} d _ 1 & b _ 1 & c _ 1 \\ \color {blue} d _ 2 & b _ 2 & c _ 2 \\ \color {blue} d _ 3 & b _ 3 & c _ 3 \end {vmatrix} \; ,\; D _ y = \begin {vmatrix} a _ 1 & \color {blue} d _ 1 & c _ 1 \\ a _ 2 & \color {blue} d _ 2 & c _ 2 \\ a _ 3 & \color {blue} d _ 3 & c _ 3 \end {vmatrix} \; ,\; D _ z = \begin {vmatrix} a _ 1 & b _ 1 & \color {blue} d _ 1 \\ a _ 2 & b _ 2 & \color {blue} d _ 2 \\ a _ 3 & b _ 3 & \color {blue} d _ 3 \end {vmatrix} \;\;\;\;\; (10)$$

مقادیر $$D_x$$، $$D_y$$ و $$D_z$$ به ترتیب از جابه‌جایی ستون $$x$$، $$y$$ و $$z$$ با ستون ثابت‌‌ها به دست می‌‌آیند.

مثال 4

جواب دستگاه سه معادله و سه مجهول زیر را با استفاده از روش کرامر بیابید.

$$\large \begin {align*} x + y- z & = 6 \\ 3 x - 2 y +z & = - 5 \\ x + 3 y - 2 z & = 1 4 \end {align*}$$

حل: با استفاده از روش کرامر داریم:

$$\large D = \begin {vmatrix} 1 & 1 & − 1 \\ 3 & − 2 & 1 \\ 1 & 3 & − 2 \end {vmatrix} , \; D _ x = \begin {vmatrix} 6 & 1 & − 1 \\− 5 & − 2 & 1 \\ 1 4 & 3 & − 2 \end {vmatrix} , \; D _ y = \begin {vmatrix} 1 & 6 & − 1 \\ 3 & − 5 & 1 \\ 1 & 1 4 & − 2 \end {vmatrix} , \; D _ z = \begin {vmatrix} 1 & 1 & 6 \\ 3 & − 2 & − 5 \\ 1 & 3 & 1 4 \end {vmatrix}$$

در نتیجه:

$$\large \begin {align*} x & = \dfrac { D _ x } { D } & = \dfrac { -3 } { - 3 } & = 1 \\ y & = \dfrac { D _ y } { D } & = \dfrac { - 9 } { - 3 } & = 3 \\ z & = \dfrac { D _ z } { D } & = \dfrac { 6 } { - 3 } & = - 2 \\ \end {align*}$$

بنابراین، جواب این معادلات برابر است با $$(1,3,−2)$$.

مثال 5

در این مثال می‌خواهیم دستگاه معادلات ناسازگار زیر را با استفاده از روش کرامر حل کنیم:

$$\large \begin {align} 3 x - 2 y & = 4\;\;\;\;\; (11) \\ 6 x - 4 y & = 0 \;\;\;\;\;(12) \end {align}$$

حل: ابتدا دترمینان‌‌های $$D$$، $$D_x$$ و $$D_y$$ را به دست می‌‌آوریم:

$$\large D = \begin {vmatrix} 3 & − 2 \\ 6 & − 4 \end {vmatrix} = 3 ( − 4 ) − 6 ( − 2 ) = 0$$

می‌‌دانیم که دترمینان صفر بدین معنی است که دستگاه معادلات یا جواب ندارد یا بی‌شمار جواب دارد. بنابراین، در اینجا باید از روش حذفی استفاده کرد. ابتدا یکی از متغیرها را حذف می‌‌کنیم.

1. معادله (۱۱) را در 2- ضرب می‌کنیم.
2- معادله حاصل را با معادله (۱۲) جمع می‌کنیم.

$$\large \begin {align*} & − 6 x + 4 y = − 8 \\ & \; \; \; \underline { 6 x − 4 y = 0 } \\ & \; \; \; \;\;\;\;\;\;\; 0 = − 8 \end {align*}$$

تساوی به دست آمده نادرست است و این یعنی اینکه دستگاه معادلات جواب ندارد. همانطور که در شکل زیر نیز دیده می‌‌شود، نمودار این دستگاه معادلات به صورت دو خط موازی است.

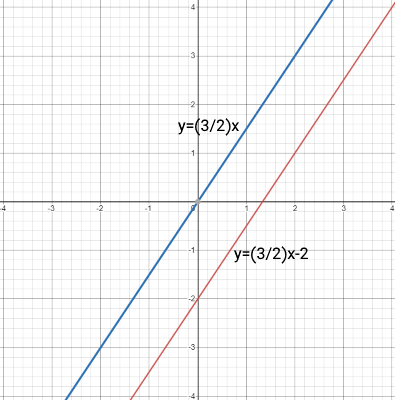
مثال 6

دستگاه معادلات وابسته زیر را با استفاده از روش کرامر حل کنید.

$$\large \begin {align} x - 2 y + 3z & = 0 \;\;\; \;\; ( 1 3 ) \\ 3 x + y - 2 z & = 0 \;\;\;\;\; ( 1 4 ) \\ 2 x - 4 y +6 z & = 0 \;\;\;\;\; ( 1 5 ) \end {align}$$

حل: ابتدا دترمینان را به دست می‌‌آوریم. برای این کار، ماتریس ضرایب را به دو ستون اول آن اضافه می‌‌کنیم:

$$\large \left| \begin{array}{ccc|cc} 1 & − 2 & 3 & 1 & - 2 \\ 3 & 1 & − 2 & 3 & 1 \\ 2 & − 4 & 6 & 2 & - 4 \end {array}\right|$$

در نتیجه:

$$\large 1 ( 1 ) ( 6 ) + ( − 2 ) ( − 2 ) ( 2 ) + 3 ( 3 )( − 4 ) −2 ( 1) ( 3 ) − ( − 4) ( − 2 ) ( 1) − 6 ( 3 )( − 2 ) = 0$$

از آنجایی که دترمینان برابر با صفر است، این دستگاه معادلات یا جواب ندارد یا بیشمار جواب دارد. بنابراین، باید روش حذفی را به کار ببریم.

۱. معادله (۱۳) را در 2- ضرب کرده و با معادله (۱۵) جمع می‌‌کنیم:

$$\large \begin {align*} & − 2 x + 4 y − 6x = 0 \\ & \; \; \underline { 2 x − 4 y + 6 z = 0 } \\ & \; \; \; \; \;\; \;\; \;\;\;\;\;\;\;\; 0 = 0 \end {align*}$$

۲. تساوی ۰=۰ عبارتی است که همواره درست است و بدین معنی است که دستگاه معادلات بی‌شمار جواب دارد. همانطور که در شکل زیر هم می‌‌بینیم، نمودار این دستگاه معادلات، دو صفحه منطبق بر هم را نشان می‌‌دهد که صفحه سوم را روی یک خط قطع می‌‌کنند.

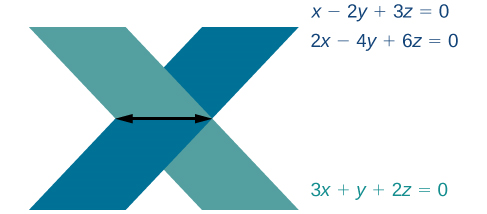
ویژگی‌‌های دترمینان

دترمینان ویژگی‌های زیادی دارد که در اینجا به برخی از آن‌ها اشاره می‌کنیم.

1. اگر ماتریس به شکل بالامثلثی باشد، دترمینان برابر با حاصلضرب درایه‌‌های قطر اصلی در جهت پایین است.
2. هنگامی که دو سطر با یکدیگر جابجا می‌‌شوند، علامت مقدار دترمینان تغییر می‌‌کند.
3. اگر دو سطر یا دو ستون یکسان باشند، دترمینان ماتریس صفر می‌‌شود.
4. در صورتی که درایه‌‌های یک سطر یا ستون ماتریس صفر باشند، دترمینان آن ماتریس برابر با صفر خواهد بود.
5. دترمینان ماتریس وارون $$A ^ {-1}$$ معکوس دترمینان ماتریس $$A$$ است.
6. اگر هر سطر یا ستون در یک ثابت ضرب شود، دترمینان نیز در همان ثابت ضرب می‌‌شود.

برای درک بهتر، این ویژگی‌‌ها را در قالب مثال زیر بررسی می‌‌کنیم.

مثال ۶

در اینجا، مثال‌هایی از ویژگی‌هایی را که بیان کردیم، ارائه می‌کنیم.

ویژگی 1: ماتریس بالامثلثی

ماتریس بالامثلثی زیر را در نظر بگیرید:

$$\large A = \begin {bmatrix} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & − 1 \end {bmatrix}$$

ماتریس $$A$$ را به دو ستون اول آن اضافه می‌‌کنیم:

$$\large A = \left[ \begin {array}{ccc|cc} 1 & 2 & 3 & 1 &2 \\ 0 & 2 &1 & 0 & 2 \\ 0 & 0 & − 1 & 0 & 0 \end {array} \right]$$

در نتیجه:

$$\large \begin {align*} \det ( A ) & = 1 ( 2 ) ( - 1) + 2 ( 1 )( 0 ) + 3( 0 ) ( 0 ) - 0 ( 2 ) (3 ) - 0 ( 1 ) ( 1 ) + 1( 0 ) ( 2 ) \\ & = - 2 \end {align*}$$

دترمینان به دست آمده برابر با حاصلضرب درایه‌‌های قطر اصلی است.

ویژگی 2: جابجایی سطرها

دترمینان ماتریس $$A$$ به صورت زیر خواهد بود:

$$\large \begin {align*} A & = \begin {bmatrix} - 1 & 5 \\ 4 & - 3 \end {bmatrix} \\ \det ( A ) & = (- 1 ) ( - 3 ) - ( 4 ) ( 5 ) \\ & = 3 - 2 0 \\ & = - 1 7 \end {align*}$$

اگر دو سطر را با یکدیگر جابه‌جا کنیم، خواهیم داشت:

$$\large \begin {align*} B & = \begin {bmatrix} 4 & - 3 \\ - 1 & 5 \end {bmatrix} \\ \det ( B ) & = ( 4 ) (5 ) - (- 1 ) ( - 3) \\ & = 2 0 - 3 \\ & = 1 7 \end {align*}$$

همان‌گونه که می‌‌بینیم، دترمینان ماتریس $$B$$ قرینه دترمینان ماتریس $$A$$ است.

ویژگی 3: یکسان بودن دو سطر یا دو ستون

$$\large \begin {align*} A & = \left[ \begin {array}{ccc|cc} 1 & 2 & 2 & 1 & 2 \\ 2 &2 & 2 & 2 & 2 \\ - 1 & 2 & 2 &- 1& 2 \end {array} \right] \\ \det ( A ) & = 1 (2 ) ( 2 ) + 2 ( 2 ) ( - 1 )+ 2 ( 2) ( 2 ) +1 ( 2) ( 2 ) - 2 ( 2 ) (1 ) - 2 (2 ) ( 2 ) \\ & = 4 - 4+ 8 +4 - 4 -8 \\ & = 0 \end {align*}$$

در اینجا به دلیل اینکه دو ستون یکسان بودند، مقدار دترمینان صفر شد.

ویژگی 4: صفر بودن درایه‌‌های یک سطر یا ستون

$$\large \begin {align*} A & = \begin {bmatrix} 1 & 2 \\ 0 & 0 \end {bmatrix} \\ \det ( A ) & = 1 ( 0) - 2 ( 0 ) \\ & = 0 \end {align*}$$

ویژگی 5: دترمینان ماتریس وارون

$$\large \begin {align*} A & = \begin {bmatrix} 1 & 2 \\ 3 & 4 \end {bmatrix} \\ \det ( A )& = 1 ( 4 ) - 3 ( 2 ) \\ & = - 2 \end {align*}$$

$$\large \begin {align*} A ^ { - 1 } & = \begin {bmatrix} - 2 & 1 \\ \dfrac { 3 } { 2} & - \dfrac { 1 } {2 } \end {bmatrix} \\ \det ( A ^ { - 1 } ) & = - 2 \left ( - \dfrac { 1 } { 2 } \right ) - \dfrac { 3} { 2 } ( 1 ) \\ & = - \dfrac { 1 } {2 } \end {align*}$$

همان‌طور که می‌‌بینیم، دترمینان ماتریس وارون $$A ^ {-1}$$ معکوس دترمینان ماتریس $$A$$ است.

ویژگی 6: ضرب یک ثابت در سطر یا ستون

$$\large \begin {align*} A & = \begin {bmatrix} 1 & 2 \\ 3 & 4 \end {bmatrix} \\ \det ( A ) & = 1( 4 ) - 2 ( 3 ) \\ & = - 2 \end {align*}$$

$$\large \begin {align*} B & = \begin {bmatrix} 2 ( 1 ) & 2 ( 2 ) \\ 3 & 4 \end {bmatrix} \\ \det ( B ) & = 2 ( 4) - 3 ( 4 ) \\ & = - 4 \end {align*}$$

چون سطر اول ماتریس $$B$$ دو برابر سطر اول ماتریس $$A$$ است، دترمینان آن نیز دو برابر دترمینان ماتریس $$A$$ خواهد بود.

مثال 7

جواب دستگاه معادلات زیر را به دست آورید.

$$\large \begin {align} 2 x + 4 y +4 z & = 2 \; \; \; \; \; ( 1 6 ) \\ 3 x +7 y + 7z & = - 5 \;\;\;\;\; ( 1 7) \\ x+2y+2z&=4 \;\;\;\;\; (18) \end{align}$$

حل: با استفاده از روش کرامر داریم:

$$\large D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}$$

طبق ویژگی 3، چون ستون دوم و سوم یکسان هستند، دترمینان برابر با صفر خواهد بود. در نتیجه، این دستگاه معادلات یا جواب ندارد یا بی‌شمار جواب دارد. برای فهمیدن این موضوع باید از روش حذفی استفاده کنیم.

معادله (۱۸) را در 2- ضرب کرده و با معادله (۱۶) جمع می‌‌کنیم:

$$\large \begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}$$

عبارت به دست آمده متناقض است و این یعنی دستگاه معادلات جواب ندارد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• قضیه کیلی همیلتون — از صفر تا صد
• استقلال خطی و ترکیب خطی — به زبان ساده
• ماتریس قطری و قطری سازی — از صفر تا صد

^^