روش نقطه میانی در حل معادله دیفرانسیل — به زبان ساده
در آموزشهای پیشین مجله فرادرس، با روشهای عددی حل معادلات دیفرانسیل، مانند روش اویلر آشنا شدیم. در این آموزش، یکی دیگر از این روشها، به نام روش نقطه میانی (Midpoint Method) را معرفی میکنیم.
روش نقطه میانی
روش نقطه میانی، روشی برای حل عددی معادله دیفرانسیل زیر است:
$$ \large y' ( t ) = f ( t , y ( t ) ) , \quad y ( t _ 0 ) = y _ 0 $$
روش نقطه میانی صریح با فرمول زیر بیان میشود:
$$ \large y _ { n + 1 } = y _ n + h f \left ( t _ n + \frac { h } { 2 }, y _ n + \frac { h } { 2 } f ( t _ n , y _ n ) \right ) , \qquad \qquad ( 1 e ) $$
فرمول روش نقطه میانی ضمنی نیز به صورت زیر است:
$$ \large y _ { n + 1 } = y _ n + h f \left ( t _ n + \frac { h }{ 2 } , \frac 1 2 ( y _ n + y _ { n + 1 } ) \right ) , \qquad \qquad ( 1 i ) $$
که در آنها $$n=0, 1, 2, \dots$$ است. در روابط بالا، $$h$$ اندازه گام (یک عدد کوچک مثبت)، $$ t _ n = t _ 0 + n h $$ و $$ y _ n $$ مقدار تقریب محاسبه شده $$ y ( t _ n ) $$ است.
روش نقطه میانی صریح به عنوان «روش اویلر اصلاح شده» (Modified Euler Method) نیز شناخته میشود. روش نقطه میانی ضمنی سادهترین «روش جابهجایی» (Collocation Method) است و به «دینامیک همیلتونی» (Hamiltonian Dynamics) اعمال میشود که یک «انتگرالگیر سیمپلتیک» (Symplectic Integrator) است.
نام روش نقطه میانی، از این موضوع ناشی میشود که در فرمول بالا، تابع $$ f $$ شیب جواب را در $$ t=t_n+h/2= \tfrac{t_n+t_{n+1}}{2} $$ نتیجه میدهد. این نقطه، نقطه میانی بین $$ t_ n $$ و $$ t _ { n + 1 } $$ است که در $$ t _ n $$ مقدار $$ y ( t) $$ را میدانیم و در $$ t _{ n + 1 } $$ میخواهیم مقدار $$ y ( t)$$ را به دست آوریم.
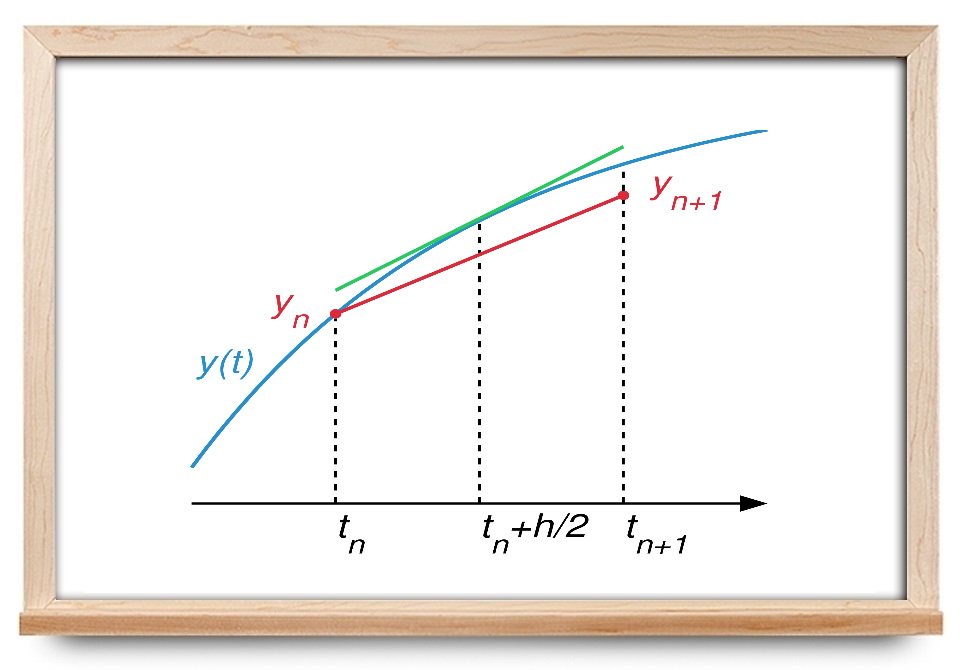
تفسیر هندسی درک شهودی بهتری را از این روش ارائه خواهد داد. شکل ۱ را در نظر بگیرید. در روش اویلر پایه، شیب خط در $$ ( t _ n , y _ n ) $$ با استفاده از $$ f ( t _ n , y _ n ) $$ محاسبه میشود. مقدار بعدی $$ y _ { n + 1 } $$ نیز در محل تقاطع خط مماس بر منحنی و خط عمودی $$ t = t _ { n + 1 } $$ به دست میآید. البته، اگر مشتق دوم بین $$ t _ n $$ و $$ t _ { n + 1 } $$ فقط مثبت یا فقط منفی باشد، منحنی به طور فزایندهای از خط مماس دور خواهد شد و با افزایش $$h$$ منجر به خطاهای بزرگتر میگردد. شکل ۱ نشان میدهد که خط مماس در نقطه میانی (سبز)، تقریب دقیقتری از منحنی در بازه ارائه میکند. البته، این شیب در نقطه میانی را نمیتوان به صورت دقیق محاسبه کرد، زیرا معادله منحنی را نمیدانیم و میخواهیم آن را محاسبه کنیم.
در واقع، شیب با استفاده از روش اویلر اصلی برای تخمین مقدار $$ y ( t) $$ در نقطه میانی و در نتیجه، محاسبه شیب خط مماس با $$ f ( ) $$ تقریب زده میشود. در نهایت، از خط مماس بهبودیافته برای محاسبه مقدار $$ y _ { n + 1 } $$ از $$ y _ n $$ استفاده میشود. این گام آخر با یک پارهخط قرمز در شکل نشان داده شده است. توجه کنید که پاره خط قرمز دقیقاً موازی خط سبز (مماس واقعی) نیست، زیرا در تخمین مقدار $$ y ( t) $$ در نقطه میانی خطا وجود دارد.
مرتبه خطای محلی در هر گام از روش نقطه میانی $$ O ( h ^ 3 ) $$ است و منجر به خطای سراسری با درجه $$ O ( h ^ 2 ) $$ میشود. بنابراین، روش نقطه میانی با اینکه محاسبات بیشتری نسبت به روش اویلر دارد، با میل اندازه گام $$h$$ به صفر، خطای آن سریعتر کاهش پیدا میکند.
استخراج روش نقطه میانی
روش نقطه میانی اصلاحی از روش اویلر $$ y_{n+1} = y_n + hf(t_n,y_n) $$ است و با روال مشابهی به دست میآید. کلید به دست آوردن روش اویلر تقریب زیر است:
$$ \large y ( t + h ) \approx y ( t ) + h f ( t , y ( t ) ) \qquad \qquad ( 2 ) $$
که از فرمول شیب به دست آمده است:
$$ \large y' ( t ) \approx \frac { y ( t + h ) - y ( t ) } { h } \qquad \qquad ( 3 ) $$
توجه کنید که $$ y' = f ( t , y ) $$.
در روش نقطه میانی، به جای معادله (۳) فرمول دقیقتر زیر را قرار میدهیم:
$$ \large y' \left ( t + \frac { h } { 2 } \right ) \approx \frac { y ( t + h ) - y ( t ) } { h } $$
در این صورت، به جای رابطه (۲)، خواهیم داشت:
$$ \large y ( t + h ) \approx y ( t ) + h f \left ( t + \frac { h }{ 2 } , y \left ( t + \frac { h } { 2 } \right ) \right ) . \qquad\qquad ( 4 ) $$
نمیتوان از این معادله برای یافتن $$ y ( t + h ) $$ استفاده کرد، زیرا مقدار $$ y$$ را در $$ t + h / 2 $$ نمیدانیم. راه حل این است که از سری تیلور برای حل $$ y ( t + h / 2 ) $$ استفاده کنیم:
$$ \large y \left ( t + \frac { h } { 2 } \right ) \approx y ( t ) + \frac { h } { 2 } y' ( t ) = y ( t ) + \frac { h } { 2 } f ( t , y ( t ) ) $$
و اگر آن را در معادله (۴) قرار دهیم، خواهیم داشت:
$$ \large y ( t + h ) \approx y ( t ) + h f \left ( t + \frac { h } { 2 } , y ( t ) + \frac { h } { 2 } f ( t , y ( t ) ) \right ) $$
که فرمول روش نقطه میانی صریح (1e) را نتیجه خواهد داد.
روش ضمنی (1i) با تقریب مقدار در نصف گام $$ t + h / 2 $$ با نقطه میانی پارهخط بین $$ y ( t) $$ تا $$ y ( t + h ) $$ به دست میآید:
$$ \large y \left ( t + \frac h 2 \right ) \approx \frac 1 2 \bigl ( y ( t ) + y ( t + h ) \bigr ) $$
و در نتیجه:
$$ \large \frac { y ( t + h ) - y( t ) } { h } \approx y' \left ( t + \frac h 2 \right ) \approx k = f \left ( t + \frac h 2 , \frac 1 2 \bigl ( y ( t ) + y ( t + h ) \bigr ) \right ) $$
قرار دادن تقریب $$ y _ n + h k $$ برای $$ y ( t _ n + h ) $$ منجر به روش رانگ کوتای ضمنی خواهد شد:
$$ \large \begin {align}
k & = f \left ( t _ n + \frac h 2 , y _ n + \frac h 2 k \right ) \\
y _ { n + 1 } & = y _ n + h \, k
\end {align} $$
که همان روش اویلر ضمنی با اندازه گام $$ h / 2 $$ است.
پیادهسازی روش نقطه میانی در متلب
کد متلب روش نقطه میانی برای معادلات اسکالر را میتوانید از این لینک [+]، کد متلب روش نقطه میانی عمومی را از این لینک [+] و کد متلب روش نقطه میانی برای یک گام را این از این لینک [+] دانلود کنید.
پیادهسازی روش نقطه میانی در پایتون
کد پایتون روش نقطه میانی بدون استفاده از کتابخانه NumPy را از این لینک [+] و کد پایتون روش نقطه میانی را که در آن از NumPy استفاده شده است، میتوانید از این لینک [+] دانلود کنید.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای محاسبات عددی
- آموزش محاسبات عددی با MATLAB
- مجموعه آموزشهای دروس ریاضیات
- آموزش ریاضی پایه دانشگاهی
- قاعده ذوزنقه ای — به زبان ساده
- روش حذفی گاوس — از صفر تا صد
- روش ژاکوبی — به زبان ساده
^^










