جمع اعداد اعشاری — به زبان ساده + تمرین و مثال

در آموزش‌های پیشین مجله فرادرس، با اعداد اعشاری و مقایسه آن‌ها آشنا شدیم. در این آموزش، مطالبی را درباره جمع اعداد اعشاری بیان می‌کنیم.

عدد اعشاری چیست؟

«عدد اعشاری» (Decimal Number) عددی است که برای نمایش مقادیری به کار می‌رود که با اعداد صحیح عادی نمی‌توان آن‌ها را بیان کرد. اعشار را با ممیز (یعنی تمایزدهنده) نمایش می‌دهیم. در دستور خط فارسی، علامت ممیز یک خط کوچک کج است. برای مثال، پنج و هفت‌دهم را به‌صورت ۵٫۷ می‌نویسیم. دقت کنید که در زبان انگلیسی، ممیز را با نقطه نشان می‌دهند. مثلاً همان عدد پنج و هفت‌دهم در زبان انگلیسی به صورت $$5.7$$ نوشته می‌شود.

نکته: توجه کنید که علامت کسر (/) با ممیز (٫) فرق دارد و اغلب به اشتباه به جای ممیز به کار می‌رود. همچنین دقت کنید که در اعداد فارسی برای اعشار از نقطه استفاده نکنید. اگر فرض کنیم می‌خواهیم چهار و شش‌دهم را به‌صورت عددی بنویسیم،‌خواهیم داشت:

• ۴٫۶ درست است.
• ۴/۶ درست نیست.
• ۴.۶ درست نیست.
• $$4.6$$ درست است.

یکی دیگر از مواردی که در رابطه با اعداد اعشاری باید به‌خاطر داشته باشیم، ارزش مکانی ارقام و نام آن‌هاست که در تصویر زیر مشخص شده است.

برای مثال، در عدد ۳٫۴۸، رقم ۳ مربوط به یکان، رقم ۴ مربوط به دهم و رقم ۸ مربوط به صدم است.

نکته: دقت کنید که وقتی ممیز در عددی به کار می‌رود، باید آن را با عدد بدون ممیز تمایز دهیم. برای مثال، عدد ۱٫۰۰۰ همان یک است و ۱۰۰۰ نمایان‌گر عدد هزار است.

نکته: قبل از عدد صحیح، هرچه صفر اضافه کنیم، عدد تغییری نمی‌کند. برای مثال، ۰۱۲٫۲۳ برابر بار ۱۲٫۲۳ است.

جمع اعداد اعشاری به معنای یافتن مجموع دو یا چند عدد اعشاری است. اگرچه جمع اعداد اعشاری شبیه به جمع اعداد صحیح است، اما نکات خاصی وجود دارد که باید هنگام جمع کردن آن‌ها رعایت شود. در ادامه، بیشتر در مورد جمع کردن اعداد اعشاری و قوانین مربوط به آن‌ها همراه با مثال بحث خواهیم کرد.

برای آشنایی با مباحث ریاضیات مدرسه، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

جمع اعداد اعشاری

جمع کردن اعداد اعشاری شبیه به جمع معمولی اعداد صحیح است. می‌دانیم که عدد اعشاری عددی است با یک جزء عددی کامل یا صحیح و یک جزء کسری دارد که با یک اعشار از هم جدا می‌شوند. با این حال، این تفاوت قوانین جمع اعداد اعشاری را تغییر نمی‌کنند.

برای جمع اعداد اعشاری، باید آن‌ها را با توجه به ارزش مقادیر مکانی آن‌ها در زیر یکدیگر تراز کنیم، اعشار را دست‌نخورده نگه داریم و سپس اعداد را جمع کنیم. باید به خاطر داشته باشیم که نمودار یا جدول ارزش مکانی اعداد اعشاری دارای مقادیر مکانی اضافه نسبت به اعداد صحیح است و آن هم ارزش مکانی است که درست بعد از نقطه اعشار می‌آید، مانند دهم، به دنبال آن صدم، هزارم و غیره.

نکات جمع اعداد اعشاری

هنگام جمع اعداد اعشاری، باید قوانینی را به خاطر بسپاریم که مفید هستند و جمع را آسان‌تر می‌کنند:

• اعداد اعشاری را به‌گونه‌ای تراز کنید که با توجه به مقادیر مکانی خود در جای درست قرار گیرند.
• همیشه، هر جا که لازم است، اعداد اعشاری را به عدد اعشاری مشابه از نظر تعداد ارقام قبل و بعد از اعشار تبدیل کنید. در جاهایی که طول اعداد اعشاری یکسان نیست، صفر را اضافه کنید.
• اکنون اعداد را جمع کنید و اعشار را در تراز با اعشار داده‌‌شده قرار دهید.

گاهی اوقات، اعداد داده شده از نظر تعداد ارقام قبل و بعد از اعشار متفاوت هستند. در چنین مواردی، اعداد اعشاری داده شده را با اضافه کردن تعداد صفرهای مورد نیاز در سمت راست اعشار به اعداد اعشار مشابه از نظر تعداد ارقام قبل و بعد از اعشار تبدیل می‌کنیم. این کار برای تسهیل فرایند جمع کردن انجام می‌شود.

به عنوان مثال، دو عدد اعشاری 0٫14 و 2٫35 اعداد اعشاری مشابهی هستند، زیرا تعداد ارقام بعد از اعشار آن‌ها با هم برابر است. این در حالی است که، اعداد 6٫32 و 6٫324 مشابه نیستند، زیرا در یکی از آن‌ها سه رقم بعد از اعشار وجود دارد و در یکی دو رقم بعد از اعشار. بنابراین، پس از اینکه اعشار داده شده به اعشار مشابه تبدیل شد، آن‌ها را جمع می‌کنیم.

روش جمع اعداد اعشاری مشابه

اعداد اعشاری مشابه دارای تعداد ارقام برابری پس از اعشار هستند. برای مثال، فرض کنید می‌خواهم جمع 2٫53 + 1٫14 را انجام دهیم. اگر به اعداد اعشاری داده شده دقت کنیم، می‌بینیم که آن‌ها از نظر تعداد ارقام مشابه هستند، بنابراین آن‌ها را به‌ترتیب در زیر هم قرار می‌دهیم و جمع را انجام می‌دهیم. در اینجا،

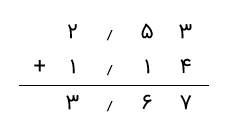
ابتدا صدم‌ها را جمع می‌کنیم: ۷ = ۴ + ۳. سپس، جمع دهم‌ها برابر با ۶ = ۱ + ۵ است. در ادامه، اعشار را می‌نویسیم. جمع یکان‌ها نیز ۳ = ۱ + ۲ است. بنابراین، حاصل جمع برابر با 3٫67 است.

روش جمع اعداد اعشاری غیرمشابه

وقتی دو عدد اعشاری تعداد ارقام متفاوتی بعد از اعشار داشته باشند، باید قبل از جمع کردن، آن‌ها مشابه کنیم. برای مثال، فرض کنید می‌خواهیم جمع 6٫3 + 2٫54 را انجام دهیم.

می‌بینیم که دو عدد اعشاری داده شده از نظر تعداد ارقام پس از اعشار متفاوت هستند، بنابراین با افزودن تعداد صفرهای مورد نیاز آن‌ها را به اعشارهای مشابه تبدیل می‌کنیم. تعداد ارقام بعد از اعشار را در هر دو عدد می‌شماریم و عدد با اعشار بیشتر را در آن‌ها تشخیص می‌دهیم. در این حالت 6٫3 دارای یک رقم پس از اعشار و 2٫54 دارای دو رقم پس از اعشار است. بنابراین، 6٫3 را به‌صورت 6٫30 می‌نویسیم. تا تعداد ارقام پس از اعشار آن با 2٫54 برابر شود. اکنون اعداد اعشاری را جمع می‌کنیم.

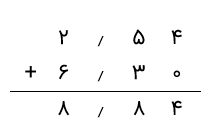
بنابراین، مجموع دو عدد اعشاری داده شده 8٫84 است.

جمع اعداد اعشاری با اعداد صحیح

روش جمع اعداد اعشاری با اعداد صحیح ساده است. بعد از عدد صحیح یک علامت  اعشار قرار می‌دهیم و تعداد صفرهای مورد نیاز را اضافه می‌کنیم تا تعداد ارقام بعد از اعشار در هر دو عدد یکسان شود. به عبارت دیگر، دو عدد را به اعداد اعشاری مشابه تبدیل می‌کنیم و سپس آن‌ها را جمع می‌کنیم.

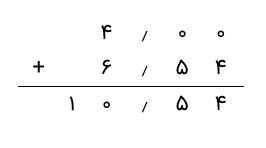
برای مثال، فرض کنید می‌خواهیم عدد 4 را با 6٫54 جمع کنیم. می‌بینیم که 4 یک عدد صحیح و 6٫54 یک عدد اعشاری است. بنابراین، باید دو عدد اعشاری با طول مساوی تشکیل دهیم. از آنجا که در 6٫54 بعد از اعشار دو رقم وجود دارد، پس از 4 یک اعشار قرار می‌دهیم و دو صفر را پس از آن اضافه می‌کنیم تا به یک عدد اعشاری با دو رقم اعشار تبدیل شود.

حالا اعداد را جمع می‌کنیم و مجموع اعداد داده شده 10٫54 می‌شود.

جمع اعداد اعشاری به روش تکنیکی

در این بخش، به جمع اعداد اعشاری به روش تکنیکی می‌پردازیم. قبل از آن، بهتر است با رقم نقلی آشنا شویم. ۲رقم نقلی رقمی است که هنگام جمع دو عدد از ستون اعداد کم‌ارزش‌تر به ستون اعداد پرارزش‌تر منتقل می‌شود.

برای مثال، دو عدد صحیح ۱۴ و ۳۸ را در نظر بگیرید. می‌خواهیم آن‌ها را جمع کنیم. ابتدا دو عدد را به شکل ستونی می‌نویسیم. سپس دو رقم یکان را جمع می‌کنیم ۱۲ = ۸ + ۴. می‌بینیم که عدد ۱۲ دو رقم دارد. رقم ۲ آن را که مربوط به یکان است، در زیر ۴ و ۸ که یکان هستند، می‌نویسیم و عدد ۱ را که دهگان است به ستون قبل، یعنی‌ دهگان‌ها منتقل می‌کنیم و با آن‌ها جمع می‌کنیم. به دلیل همین انتقال، به این رقم نقلی می‌گویند. تصویر زیر، جمع دو عدد را به‌خوبی نشان می‌دهد.

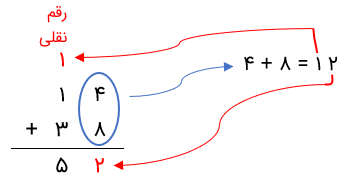
جمع کردن اعداد اعشاری با رقم نقلی مشابه چیزی است که در جمع اعداد صحیح انجام می‌شود. علاوه بر این، اگر مجموع ارقام در هر یک از ستون‌ها بزرگ‌تر از 9 باشد، با انتقال رقم اضافی به ستون قبل، جمع را انجام می‌دهیم. در ادامه، نحوه جمع کردن اعداد اعشاری را با رقم تقلی با مثال زیر بیان می‌کنیم.

فرض کنید می‌خواهیم جمع 14٫62 + 12٫63 را انجام دهیم.

گام ۱: ابتدا اعداد داده شده را با توجه به ستون‌های ارزش مکانی مربوطه تراز می‌کنیم و در صورت نیاز آن‌ها را به اعداد اعشاری مشابه تغییر می‌دهیم. اطمینان حاصل می‌کنیم که اعشار با یکدیگر تراز باشند.

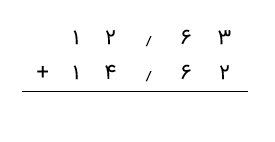
گام ۲: در ادامه، شروع به جمع ارقام در هر ستون به صورت جداگانه می‌کنیم. از سمت راست شروع کرده و با حرکت به سمت چپ، به همان روشی که برای اعداد صحیح انجام می‌دهیم، کار را ادامه می‌دهیم. اعداد داده شده در ستون صدم را جمع می‌کنیم (2 + 3 = 5) و 5 را زیر ستون می‌نویسیم.

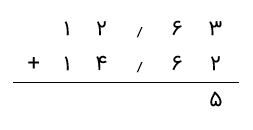
گام ۳: به ستون دهم‌ها می‌رویم و جمع 6 + 6 = 12 را انجام می‌دهیم. همان‌طور که می‌دانیم، نمی‌توانیم ۱۲ را در زیر این ستون قرار دهیم، زیرا می‌توانیم فقط یک رقم زیر هر ستون بنویسیم. بنابراین، مشابه آنچه برای جمع اعداد صحیح گفتیم، رقم نقلی را به ستون سمت چپ منتقل می‌کنیم. بنابراین، از عدد ۱۲، در زیر این ستون عدد 2 را می‌نویسیم و عدد 1 را به ستون قبلی، یعنی ستون یکان می‌بریم. این 1 (رقم نقلی) با اعداد در ستون یکان‌ها جمع می‌شود. به یاد داشته باشید که ممیز را زیر ستون ممیز قرار دهید.

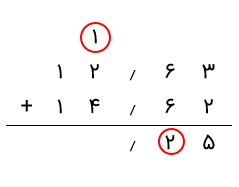
گام ۴: اکنون اعداد زیر ستون یکان‌ها را جمع می‌کنیم. در اینجا، پس از قرار گرفتن حامل یا همان رقم نقلی در این ستون، به همراه سایر اعداد جمع می‌شود و نتیجه این خواهد شد: 4 + 2 + 1 = 7.

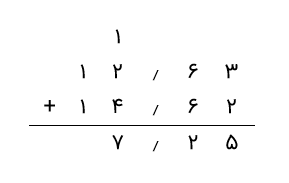
گام 5: در نهایت اعداد داده شده در ستون دهگان را جمع می‌کنیم، یعنی 1 + 1 = 2.

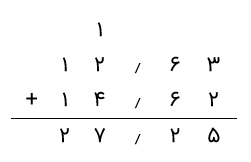
بنابراین، مجموع اعداد 14٫62 و 12٫63 برابر با 27٫25 است.

جمع اعداد اعشاری به روش فرایندی

در این بخش، به جمع اعداد اعشاری با روش فرایندی می‌پردازیم. در روش تکنیکی، از راست به چپ اعداد مربوط به هر ستون را جمع می‌کردیم. در روش فرایندی از چپ به راست حرکت می‌کنیم. با یک مثال، این فرایند را شرح می‌دهیم.

فرض کنید می‌خواهم دو عدد اعشاری ۳٫۳۲۵ و ۱٫۴۷۴ را با هم جمع کنیم. بدین منظور، مراحل زیر را طی می‌کنیم.

گام ۱: ابتدا یکی از دو عدد را می‌نویسیم. برای مثال، ما عدد ۳٫۳۲۵ را نوشته‌ایم.

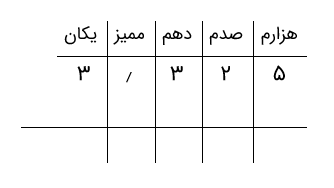
گام ۲: از سمت چپ شروع می‌کنیم. یکان عدد دیگر را با یکان عددی که نوشته‌ایم جمع می‌کنیم. یکان عدد ۱٫۴۷۴ رقم ۱ است. جمع یکان‌ها ۴ می‌شود.

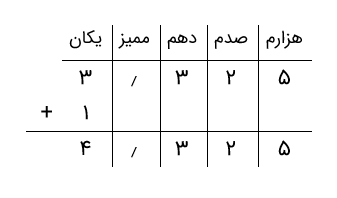
گام ۳: کنون حاصل جمع مرحله قبل را بالا می‌نویسیم و رقم بعدی عدد ۱٫۴۷۴، یعنی دهم (رقم ۴) را می‌نویسیم و جمع می‌کنیم. تصویر زیر این موضوع را به‌خوبی نشان می‌دهد.

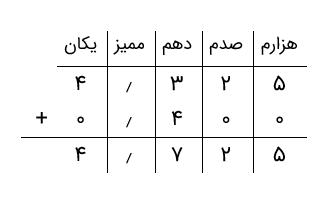
گام ۴: حال، عدد جدید را بالا می‌نویسیم و این بار رقم صدم عدد ۱٫۴۷۴ (یعنی رقم ۷) را با آن جمع می‌کنیم.

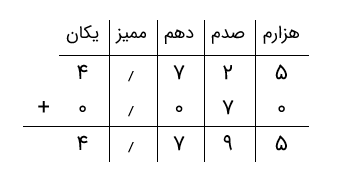
گام ۵: اکنون، جواب به‌دست‌آمده را در بالا می‌نویسیم و رقم هزارم عدد ۱٫۴۷۴، یعنی ۴ را با آن جمع می‌کنیم.

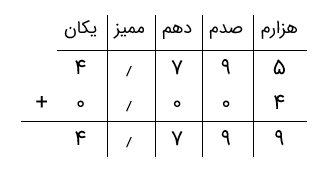
بنابراین، جواب جمع دو عدد اعشاری ۳٫۳۲۵ و ۱٫۴۷۴ برابر با ۴٫۷۹۹ است.

جمع اعداد اعشاری با شکل

برای جمع اعداد اعشاری با کمک شکل، باید اعداد را با شکل نشان دهیم. با یک مثال ساده این موضوع را شرح می‌دهیم. فرض کنید می‌خواهیم دو عدد ۱٫۰۱ و ۱٫۰۵ را با هم جمع کنیم. ابتدا شکل‌های این دو عدد را رسم می‌کنیم. چون دو رقم اعشار، یعنی صدم، داریم. پس واحدها باید به صد قسمت تقسیم شوند.

شکل‌ زیر این دو عدد را نمایش می‌دهند.

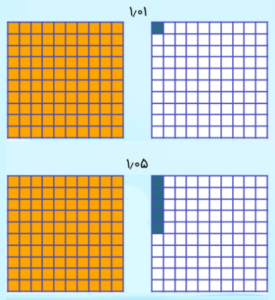
برای جمع، کافی است تعداد واحدهای کامل و تعداد خانه‌ها را بشماریم. همان‌طور که می‌بینیم، دو واحد کامل داریم که با رنگ نارنجی مشخص شده‌اند. تعداد خانه‌های آبی نیز مجموعاً ۶ عدد است. پس در کل ۲ واحد کامل و ۶ خانه کوچک داریم. بنابراین، عدد اعشاری حاصل‌جمع برابر با ۲٫۶ است.

جمع اعداد اعشاری با تقریب

یکی دیگر از روش‌های جمع اعداد اعشاری، انجام جمع با در نظر گرفتن تقریب است. این کار را می‌توانیم به دو روش انجام دهیم. در قالب یک مثال، این دو روش را معرفی می‌کنیم.

فرض کنید می‌خواهیم جمع دو عدد ۴٫۵ و ۳٫۲ را انجام دهیم. در ادامه، دو روش را بررسی می‌کنیم.

روش اول: در روش اول، می‌توانیم طبق روش‌هایی که پیش‌تر گفتیم، دو عدد را جمع کنیم، سپس جواب را تقریب بزنیم. بدین منظور، ابتدا دو عدد را جمع می‌کنیم:

۷٫۷ = ۴٫۵ + ۳٫۲

جواب به‌دست‌آمده برابر با ۷٫۷ است. حال این عدد را تقریب می‌زنیم. ابتدا می‌بینیم که این عدد بین دو عدد صحیح ۷ و ۸ قرار دارد. همچنین، مشاهده می‌کنیم که ۷٫۷ به عدد ۸ نزدیک‌تر است. بنابراین، جواب تقریبی برابر با ۸ خواهد بود.

روش دوم: در روش دوم، تقریب را در ابتدای کار اعمال می‌کنیم. بدین صورت که ابتدا دو عددی را که می‌خواهیم با هم جمع کنیم تقریب می‌زنیم. عدد ۴٫۵ به عدد ۵ تقریب زده می‌شود و تقریب عدد  ۳٫۲، عدد ۳ است. بنابراین، در اینجا دو عدد تقریبی ۵ و ۳ را باید با هم جمع کنیم.

۸ = ۵ + ۳

در نتیجه، جواب تقریبی برابر با ۸ خواهد بود.

جمع اعداد اعشاری روی محور

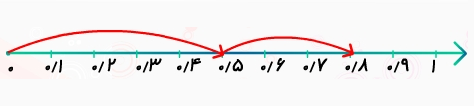
برای جمع اعداد اعشاری روی محور، ابتدا با یک کمان عدد نخست را مشخص می‌کنیم. سپس از انتهای کمان اول کمان مربوط به عدد دوم را رسم می‌کنیم. انتهای کمان دوم نشان‌دهنده حاصل‌جمع است.

برای مثال، فرض کنید می‌خواهیم دو عدد ۰٫۵ و ۰٫۳ را با هم جمع کنیم. ابتدا عدد ۰٫۵ را روی محور مشخص می‌کنیم. برای این کار، از صفر شروع کرده و کمانی به‌طول ۰٫۵ رسم می‌کنیم. از انتهای کمان اول، کانی به طول سه واحد یک‌دهم رسم می‌کنیم که نشان‌دهنده عدد اعشاری ۰٫۳ است. می‌بینیم که انتهای این کمان روی عدد ۰٫۸ قرار دارد. بنابراین، جواب جمع دو عدد برابر با ۰٫۸ است.

مثال‌های جمع اعداد اعشاری

در این بخش، چند مثال را از جمع اعداد اعشاری بررسی می‌کنیم.

مثال اول

دو عدد $$2\frac 18$$ و $$3.03$$ را با هم جمع کنید.

جواب: ابتدا باید عدد مخلوط را به عدد اعشاری تبدیل کنیم. بدین منظور، ابتدا آن را به یک کسر متعارفی تبدیل می‌کنیم:

$$2\frac 18 = \frac {2\times 8 + 1}{8} = \frac {17 }{8}$$

مخرج این کسر $$8$$ است و باید آن را به یک عدد مضرب $$10$$ تبدیل کنیم. با ضرب آن در $$125$$ به $$1000$$ می‌رسیم که مضرب $$10$$ است. بنابراین، خواهیم داشت:

$$\frac {17 } {8} = \frac {17 \times 125}{8\times 125} = \frac {2125}{1000}$$

اکنون، صورت کسر را می‌نویسیم، و از راست سه رقم اعشار را جدا می‌کنیم:

$$2.125$$

برای آشنایی بیشتر با تبدیل عدد مخلوط به کسر، به آموزش «تبدیل عدد مخلوط به کسر — به زبان ساده + حل تمرین و مثال» مراجعه کنید.

بنابراین، باید دو عدد اعشاری ۲٫۱۲۵ و ۳٫۰۳ را با هم جمع کنیم. بدین منظور، دو عدد را با رعایت ارزش مکانی ارقامشان می‌نویسیم و جمع را انجام می‌دهیم. باید عدد ۳٫۰۳ را به‌صورت ۳٫۰۳۰ بنویسیم، زیرا عدد ۲٫۱۲۵ سه رقم اعشار دارد.

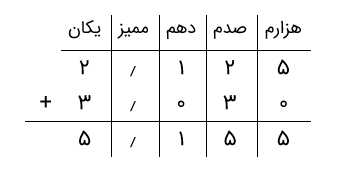
بنابراین، جواب ۵٫۱۵۵ است.

مثال دوم

عدد $$\frac 3 {16}$$ را با $$1.005$$ جمع کنید.

جواب: ابتدا باید کسر را به باید ببینیم عدد $$16$$ را در چه عددی ضرب کنیم تا حاصل مضربی از $$10$$ شود. اگر از ماشین حساب کمک بگیریم، با کمی سعی و خطا به عدد $$625$$ می‌رسیم و خواهیم داشت:‌

$$\frac {3 } {16} = \frac {625 \times 3}{625\times 16} = \frac {1875}{10,000}$$

اکنون، عدد صورت، یعنی $$1875$$ را می‌نویسیم، و از راست چهار رقم اعشار را جدا می‌کنیم:

$$0.1875$$

برای آشنایی بیشتر با تبدیل کسر به اعشار، به آموزش «تبدیل کسر به اعشار — به زبان ساده + حل تمرین و مثال» مراجعه کنید.

بنابراین، باید دو عدد ۰٫۱۸۷۵ و ۱٫۰۰۵۰ را با هم جمع کنیم. بدین منظور، دو عدد را زیر هم می‌نویسیم و از سمت راست شروع می‌کنیم و ارقام را جمع می‌کنیم. جمع ده‌هزارم‌ها برابر با ۵ است. در ادامه، می‌بینیم که جمع دو رقم ۵ و ۷ در ستون هزارم دو عدد، برابر با ۱۲ می‌شود و یک رقم نقلی خواهیم داشت. در پایین مقدار ۲ را می‌نویسیم و رقم ۱ را به ستون صدم‌ها منتقل می‌کنیم. سپس جمع ارقام ستون صدم را انجام می‌دهیم که برابر با ۹ = ۰ + ۸ + ۱ است. جمع ارقام ستون دهم نیز برابر با ۱ = ۰ + ۱ است. جمع یکان‌ها نیز ۱ = ۱ + ۰ است.

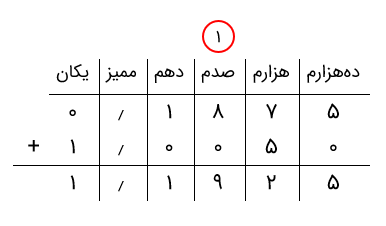
مثال سوم

دو عدد اعشاری ۰٫۶ و ۰٫۱۳ را با رسم شکل جمع کنید.

جواب: ابتدا دو عدد را در قالب شکل نشان می‌دهیم.

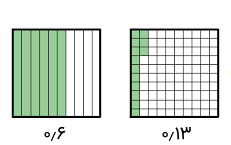
برای جمع کردن دو عدد، کافی است خانه‌های رنگ‌شده دو شکل را در یک شکل بیاوریم و آن‌ها را بشماریم.

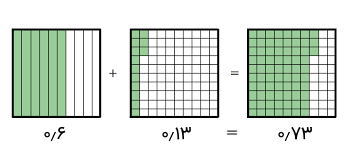
می‌بینیم که ۷ ردیف ده‌تایی و ۳ خانه که هرکدام برابر با یک‌صدم هستند، داریم. بنابراین، جواب ۰٫۷۳ است.

مثال چهارم

شکل زیر، جمع چه اعدادی روی محور را نشان می‌دهد و حاصل این جمع چه عددی است؟

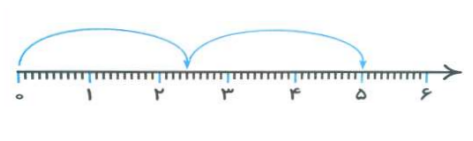
جواب: اگر فواصل را بشماریم، می‌بینیم که انتهای کمان اول، عدد ۲٫۴ را نشان می‌دهد. تعداد خانه‌های کمان دوم از انتهای کمان اول نیز دو واحد کامل و ۶ واحد دهم است که نشان‌دهنده عدد ۲٫۶ خواهد بود. انتهای کمان دوم حاصل‌جمع دو عدد را نشان می‌دهد که برابر با ۵ است.

مثال پنجم

جمع دو عدد ۳٫۳۳ و ۳۳٫۳ را بنویسید.

جواب: عدد ۳۳٫۳ را به‌صورت ۳۳٫۳۰ می‌نویسیم تا تعداد رقم‌های بعد از اعشار دو عدد برابر شود. عدد ۳٫۳۳ را نیز به‌صورت ۰۳٫۳۳ می‌نویسیم تا تعداد ارقام قبل از اعشار نیز برابر شود. بنابراین، جمع به‌صورت زیر انجام می‌شود.

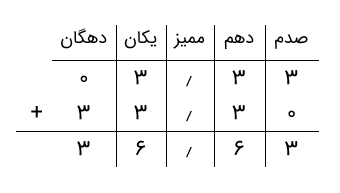
بنابراین، جمع دو عدد برابر با ۳۶٫۶۳ است.

مثال ششم

قد مهرنوش ۱٫۵۲ متر است قد دوستش، نرگس، ۰٫۳ متر از او بیشتر است. قد نرگس را محاسبه کنید.

جواب: کافی است حاصل‌جمع ۱٫۵۲ و ۰٫۳ را به‌دست آوریم.

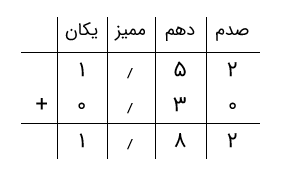
بنابراین، قد نرگس ۱٫۸۲ متر است.

جمع‌بندی

در این آموزش، ضمن معرفی اعداد اعشاری با روش‌های جمع کردن آن‌ها آشنا شدیم و دو روش رایج و مهم جمع فرایندی و جمع تکنیکی این اعداد را گام به گام شرح دادیم. در پایان نیز به حل مثال‌هایی از جمع اعداد اعشاری پرداختیم.