تقریب خطی – به زبان ساده (+ دانلود فیلم آموزش رایگان)
در این آموزش از مجموعه آموزشهای ریاضیات مجله فرادرس، یکی از کاربردهای مهم مشتق بهنام تقریب خطی را بیان میکنیم. تقریب خطی، بهمعنای پیدا کردن یک تابع خطی برای توابع غیرخطی است.


فیلم آموزشی تقریب خطی
برای تابع ، میتوان شیب را در نقطه بهدست آورد. در نتیجه، معادله خط مماس که آن را مینامیم، بهصورت زیر است:
این خط در شکل زیر نشان داده شده است.
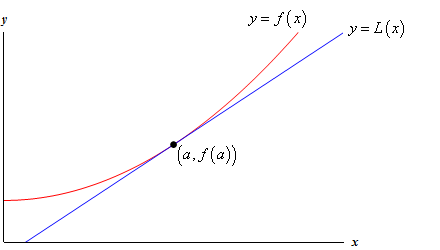
با توجه به نمودار شکل بالا میتوان مشاهده کرد که در نزدیکی ، تابع و خط مماس، شکل تقریباً برابری دارند. در این حالت، خط مماس بر تابع را در نقطه تقریب خطی مینامیم.
اما چرا این کار را انجام میدهیم؟ مثال زیر، این موضوع را به خوبی نشان میدهد.
مثال ۱
تقریب خطی تابع را در بهدست آورید. با استفاده از این تقریب خطی، مقادیر و را محاسبه کنید.
حل: از آنجایی که بهدست آوردن خط مماس بر منحنی کار آسانی است، تقریب خطی را میتوان بهراحتی بهدست آورد:
در نتیجه، تقریب خطی بهصورت زیر خواهد بود:
اکنون مقادیر و را در تقریب خطی قرار داده و مقادیر خواستهشده را محاسبه میکنیم. برای مقایسه، مقادیر دقیق را نیز آوردهایم:
همانطور که میبینیم، در تقریب خطی نتیجه مطلوبی دارد و به مقدار واقعی بسیار نزدیک است. اما نتیجه در رضایتبخش نیست. اگر کمی فکر کنیم، میبینیم که این نتیجه خیلی هم عجیب نیست. در نزدیکی ، تابع و تقریب خطی آن، شیب یکسانی دارند و هردو از نقطه میگذرند. هرچه از نقطه دور شویم، تقریب خطی شیب ثابتی دارد، اما شیب تابع، با تغییر تغییر میکند، در نتیجه تابع و تقریب خطی آن، از یکدیگر دور میشوند.
شکل زیر، نمودار تابع و تقریب خطی آن را نشان میدهد.
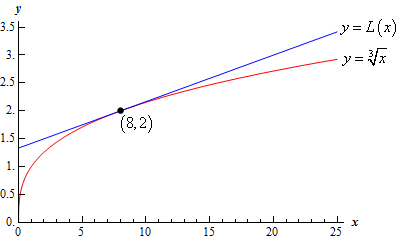
بنابراین، میتوان گفت تقریبهای خطی، در نزدیکی عملکرد مطلوبی دارند و هرچه از این نقطه دور شویم، اختلاف تقریب از مقدار واقعی، بیشتر میشود. سؤال مهمی که پیش میآید این است که برای آنکه تقریب مطلوب باشد، باید چه اندازه به نقطه نزدیک شویم؟ این موضوع به تابع و مقدار بستگی دارد. اغلب، پیشبینی اینکه تا چه حد از دور شویم و تقریب همچنان مناسب باشد، کار آسانی نیست.
مثال ۲
تقریب تابع را در بهدست آورید.
حل: برای محاسبه تقریب خطی، باید خط مماس بر را در بهدست آوریم. ابتدا مقدار تابع و مشتق آن را محاسبه میکنیم:
در نتیجه، تقریب خطی بهصورت زیر خواهد بود:
بنابراین، برای مقادیر کوچک میتوان گفت: .
تقریب خطی ابزار مهمی است که در علوم مختلف کاربردهایی مانند سادهسازی فرمولها دارد. این تقریب همچنین به توصیف پدیدههای غیرخطی کمک میکند.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- مجموعه آموزشهای مدلسازی، برازش و تخمین
- مجموعه آموزشهای محاسبات عددی
- آموزش ریاضیات عمومی ۱
- آموزش محاسبات عددی با MATLAB
- دستگاه معادلات خطی — به زبان ساده
- روش نیوتن — به زبان ساده
- خطی سازی سیستم های غیرخطی — از صفر تا صد
^^













سلام
به نظرم جای/؛تقریب های خطی با استفاده از مشتقات جزیی/ خالی هست
لطفا تقریب خطی در توابع چند متغیره را هم اضافه کنید
سپاسگزارم
سپاس از تدریس بی نظیرتان
ممنونم.عالی بود مهندس.
ای کاش طریقه بدست اوردن بقیه جملات رو هم بگید.