تعیین جرم کهکشان ها — به زبان ساده

احتمالاً همیشه برای تعیین مشخصات یک جرم آسمانی آن را در گوگل سرچ کرده‌اید و کم و بیش به جواب خود رسیده‌اید. اما آیا تاکنون از خود پرسیده‌اید که این اندازه‌گیری‌ها از اجرام آسمانی با فاصله‌های دور چگونه صورت می‌گیرد؟ مسلماً برای تعیین جرم کهکشان ها نمی‌توان آن‌ها را روی ترازو گذاشت و عدد آن را یادداشت و اعلام کرد. در حقیقت در نجوم و کیهان‌شناسی برای تعیین هر یک از این پارامترها روش‌های متفاوتی وجود دارد که هر کدام از آن‌ها با درجه‌ای از خطا روبه‌رو است.

در این مطلب قصد داریم روش‌های تعیین جرم کهکشان‌ ها را بررسی کنیم. اگرچه در این مطلب سه روش تعیین جرم کهکشان ها را به شکل خلاصه شرح خواهیم داد اما نباید انتظار داشت جواب‌های حاصل از این روش‌ها کاملاً یکسان باشند زیرا در این روش‌ها ماده تاریک به صورت یکسان در محاسبات در نظر گرفته نمی‌شود و این موضوع سبب می‌شود که نتایج به دست آمده یکسان نباشند.

در حقیقت باید گفت که به دلیل مشکل در تخمین اندازه و نحوه توزیع ماده تاریک در راه شیری، میزان زیادی ابهام در تعیین جرم این کهکشان نیز وجود دارد. همین مشکل در مورد تعیین جرم سایر کهکشان‌ ها نیز است. با در نظر گرفتن تمام خطاهای موجود در تعیین این کمیت، برای آنکه بدانید تعیین جرم کهکشان ‌ها چگونه است مطالعه این مطلب را از دست ندهید.

تعیین جرم کهکشان‌ ها از طریق منحنی چرخش 

اصول اولیه این روش تقریباً ساده است، منحنی چرخش یک کهکشان رصد می‌شود و با منحنی چرخش تئوری پیش‌بینی شده همان کهکشان مقایسه می‌شود. در این مقایسه باید جرم قرار گرفته درون هاله ماده تاریک نیز به شکل منطقی در نظر گرفته شود. برای ورود به بحث از روش‌های تعیین جرم کهکشان راه شیری شروع می‌کنیم و در ادامه این موضوع را برای گروه‌های دیگر کهکشانی نیز بسط می‌دهیم.

تعیین جرم کهکشان راه شیری

از بررسی‌های انجام شده می‌دانیم خورشید حدود 240 میلیون سال نياز دارد تا یک دور کامل پیرامون مرکز راه شیری بزند. برای به دست آوردن این مقدار شما باید سرعت گردش خورشید در مدارش و نیز فاصله آن از مرکز راه شیری را داشته باشید.

سرعت گردش خورشید در دهه 20 میلادی توسط «برتیل لیندبلاد» (Bertil Lindblad) (1956-1895) و «جان هندریک» (Jan Hendrik) (1992-1900) از طریق بررسی حرکت ستاره‌های جمعیت$$I$$ نسبت به ستاره‌های جمعیت$$II$$ به دست آمد. در مورد جمعیت ستاره‌ای و ویژگی‌های آن‌ها این مطلب را بخوانید.

همانگونه که در مطلب مربوط به جمعیت ستاره‌ای گفته شد، ستاره‌های جمعیت$$II$$ حرکت چرخشی خالص کوچکی نسبت به مرکز کهکشان راه شیری دارند و به همین دلیل به عنوان مرجعی برای تعیین حرکت خورشید استفاده می‌شوند.

ستاره‌های جمعیت$$I$$ در محدوده ما در راه شیری با سرعتی معادل $$220\ km\ s^{-1}$$ در حال حرکت هستند. از این اطلاعات می‌توان برای محاسبه جرم بخش درونی راه شیری استفاده کرد. نمودار سرعت بر حسب فاصله از مرکز برای بخش‌های متفاوت یک سیستم چرخشی منحنی چرخش نامیده می‌شود.

منحنی چرخش برای یک چرخ صلب با قطر 3 متر که در هر ثانیه یک دور می‌زند در شکل اول تصویر (۱) نمایش داده شده است. همانگونه که شکل نشان می‌دهد، سرعت (که معمولاً با واحد متر بر ثانیه بیان می‌شود) هر نقطه از چرخ نسبت به فاصله از مرکز افزایش می‌یابد.

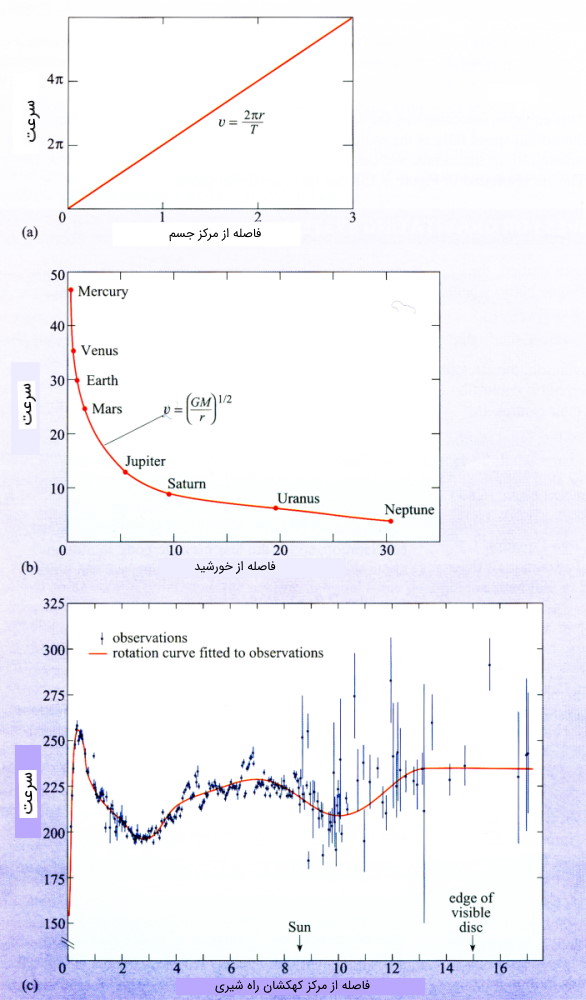
توجه داشته باشید در مورد یک چرخ صلب سرعت زاویه‌ ای هر نقطه پیرامون مرکز (يعنی مقدار زاويه‌ای كه در هر ثانيه از ديد ناظر مركز چرخ طی می‌شود) یکسان است و یعنی هر بخش از این قطعه صلب سرعت زاویه ای یکسان دارد. این ویژگی چرخش یک جسم صلب است.

شکل دوم در تصویر (۱)، نمودار گردش یک سیاره به دور خورشید را نشان می‌دهد. مقدار زمان لازم برای گردش هر سياره به دور خورشيد متفاوت است و به همين دليل است که هريك از سياره‌ها با سرعت‌های زاویه ‌ای متفاوت حرکت می‌کنند.

این ویژگی چرخش دیفرانسیلی است و به وضوح با گردش جسم صلب متفاوت است. همانگونه که از شکل دوم تصویر (۱) می‌توان دید نمودار چرخش برای چنین سیستمی خطی نیست، بنابراین سرعت و فاصله از مركز با یکدیگر متناسب نیستند.

شکل سوم تصویر (۱) نمودار چرخش راه شیری را نمایش می‌دهد. این شکل با شکل دوم متفاوت است و نشان می‌دهد که رابطه مستقیمی بين سرعت و فاصله از مرکز وجود ندارد و بنابراین چرخش دیفرانسیلی را به وسيله بازه‌ای از سرعت‌های زاويه‌ای نمایش می‌دهد. تفاوت بین شکل‌های دوم و سوم در تصویر (۱) به این دلیل است که جسمی مرکزی و متراکم در مرکز راه شیری وجود ندارد در حالی که در منظومه شمسی خورشید وجود دارد و بر حرکت سیارات تاثیر می‌گذارد.

محاسبه جرم سیستم‌های گرانشی

معادله‌ای که نمودار چرخش یک جسم که توسط نیروی جاذبه یک جسم مرکزی دیگر به وجود می‌آید را نشان می‌دهد، بیان می‌کند که سرعت درون مدار و شعاع مدار به جرم جسم مرکزی ارتباط دارد.

این رابطه در نجوم بسیار مهم است از آن جهت که این امکان را فراهم می‌آورد که جرم جسم مرکزی را از گردش اجرام اطراف آن محاسبه کنیم.

برای یک جرم در مدار دایره‌ای با شعاع $$r$$ که پیرامون یک جسم بسیار سنگين‌تر $$M$$ در حال گردش است، فرمول مربوط به منحنی چرخش برابر است با:

$$v=(\frac{GM}{r})^{\frac{1}{2}}$$

این رابطه نشان می‏‌دهد که سرعت $$v$$ با $$\frac{1}{r^{\frac{1}{2}}}$$ متناسب و بدین معناست که با افزايش شعاع از سرعت کاسته می‌شود. این معادله را به شکل خلاصه می‌توان به صورت $$v\propto \frac{1}{r^{\frac{1}{2}}}$$ نوشت. شکل دوم تصویر (۱) از طریق همین رابطه به دست می‌آید.

بنابر قانون دوم حرکت نیوتون مقدار شتاب $$a_i$$ برای جسم $$i$$ با جرم $$m_i$$ و تحت نیروی $$F$$ برابر است با:

$$a_i=\frac{F}{m_{i}}$$

همچنین بر اساس قانون جاذبه نیوتون نیروی گرانش بین دو جسم نقطه‌ای با جرم‌های m و M که فاصله بین مرکزهای آن‌ها $$r$$ است برابر با $$F_g=\frac{G\ Mm}{r^{2}}$$ است که در آن G ثابت جهانی گرانش و برابر با $$6.673 \times 10^{-11}\ N m^2\ kg^{-2}$$ fi به دست می‌آید.

با جایگزین کردن مقدار $$F_g$$ در رابطه مربوط به قانون دوم نیوتن شتاب به صورت زیر به دست خواهد آمد:

$$a_{g,m}=\frac{\frac{GMm}{r^{2}}}{m}=\frac{GM}{r^{2}}$$
$$a_{g,M}=\frac{\frac{GMm}{r^{2}}}{M}=\frac{Gm}{r^{2}}$$

در مواردی که $$M$$ بسیار بزرگتر از $$m$$ یعنی $$\frac{GM}{r^{2}}\gg \frac{Gm}{r^{2}}$$ است، شتاب جسم سنگین‌تر $$a_{g,M}$$ بسیار کمتر از شتاب جسم سبک‌تر $$a_{g,m}$$ خواهد شد.

بنابراین اجسام سنگین‌تر به سختی حرکت می‌کنند و می‌توان آن‌ها را به عنوان مرجعی ساکن برای اجسام سبک‌تر در نظر گرفت. یک شکل ساده و ویژه این حرکت برای جسمی سبک است كه با سرعتی ثابت حول جسم بسیار سنگین در مدار دایره‌ای می‌چرخد، اين نوع حرکت را حرکت دايره‌ای یکنواخت می‌نامیم.

بر همین اساس در این حرکت هر جسمی که با سرعت $$v$$ حول مرکزی به شعاع $$r$$ در حال گردش است همواره باید در حال شتاب گرفتن باشد. این شتاب به نام شتاب جانب مرکز شناخته می‌شود و جهت آن همواره به سمت مرکز و مقدار آن برابر با $$a_{cen}=\frac{v^{2}}{r}$$ است.

هنگامی که حرکت دايره‌ای یکنواخت در نتیجه جاذبه گرانشی بین دو جسم به وجود آید، شتاب جانب مرکز برابر با شتاب گرانشی است و جسم سبک‌تر حول جسم ثابت و سنگین دوران می‌کند لذا داریم:

$$a_{cen}=a_{g,m}$$
$$\frac{v^{2}}{r}=\frac{GM}{r^{2}}$$

رابطه بالا را می‌توان بر حسب سرعت و جرم جسم مرکزی بازنویسی کرد و داریم:

$$v=(\frac{GM}{r})^{\frac{1}{2}}$$
$$M=\frac{v^{2}r}{G}$$

توجه داشته باشید سرعت جسم سبک‌تر در مدار به جرم آن بستگی ندارد. همچنین توجه کنید که می‌توان جرم جسم مرکزی را از سرعت و شعاع حرکت جسم در حال چرخش بدون دانستن جرم جسم کوچکتر که در حال چرخش است محاسبه کرد.

حال می‌توانید متوجه شوید که محاسبه جرم جسمی مانند خورشید چه قدر ساده است. تمام چیزی که لازم داريد سرعت و شعاع گردش یک جسم حول جسمی دیگر است، حتی نيازی به دانستن جرم جسم کوچکتر نیز وجود ندارد.

با استفاده از این اطلاعات اینک می‌خواهیم جرم بخش داخلی كهكشان را محاسبه كنيم. برخلاف منظومه شمسی، راه شیری یک جرم مرکزی و سنگین در مرکز خود ندارد و در عوض حرکت اجزای آن تحت تأثیر جاذبه اجزای دیگر قرار دارند و به این دلیل تحلیل‌های دقیق از آن بسیار پیچیده است. اما باز هم این امکان وجود دارد که بتوان یک تخمین ساده از جرم بخش داخلی راه شیری به دست آورد.

اساس این محاسبه بر نظریه گرانش نیوتنی استوار است و بیان می‌کند هنگامی که جرم یک سیستم در کره‌ای متقارن پیرامون نقاط مرکزی آن توزیع شده باشد، برآیند نیروی جاذبه كه به یک جسم نقطه‌ای (بسيار كوچک) با شعاع معلوم وارد می‌شود تنها به جرم داخل شعاع آن نقطه تا مرکز بستگی خواهد داشت. بنابراین برآیند نیروی جاذبه با حالتی که تمام جرم در مرکز متمرکز شده باشند برابر است.

در مورد راه شیری گفتیم که توزیع جرمی ستاره‌ها کاملاً متقارن نیست اما جرمی كه خارج از یک شعاع مشخص قرار دارد تأثیر اندكی بر نیروی جاذبه خواهد داشت و هم چنان می‌توان با استفاده از روش بالا تخمین قابل قبولی از جرم بخش داخلی راه شیری ارائه داد.

اگر این روش محاسبه را برای تعیین جرم کهکشان راه شیری قبول کنیم آنگاه می‌توان سرعت گردش در مدار رصد شده در شعاعی مانند $$r$$ را در فرمول‌های منحنی چرخش قرارداد تا جرم بخش داخلی این شعاع را بدست آورد.

از آنجا که این کمیت جرم داخلی شعاع $$r$$ است و تمام جرم راه شیری نیست، این جرم را با علامت $$M(r)$$ مشخص می‌کنیم.

سوال: الف) جرم کهکشان راه شیری را در فاصله بین خورشید تا مرکز راه شیری محاسبه کنید. (جواب‌ها را در سیستم SI و با استفاده از جرم خورشید ارائه دهید $$M_{\odot}=1.99 \times 10^{30} \mathrm{~kg}$$) (راهنمایی: در حال حاضر می‌دانیم که خورشید $$8.5\ kpc$$ از مرکز راه شیری فاصله دارد و سرعت گردش آن در مدار حدوداً دایره‌ای برابر با $$220\ \frac{km}{s}$$ است). ب) در صورت استفاده از قوانین ریاضی معمول جواب‌های به دست آمده چه تفاوتی داشتند؟ آیا دلیل فیزیکی برای انحراف از این قوانین وجود دارد؟

پاسخ: الف) برای استفاده از معادله $$M(r)=\frac{v^{2}r}{G}$$ دانستن سرعت حرکت خورشید ($$v$$)، شعاع مدار ($$r$$) و نیز ثابت جهانی گرانش یا G لازم است. بدین ترتیب داریم:

$$\begin{array}{l} M_{M w}(8.5 k p c)=v^{2} r / G \\ =\left(220 \times 10^{3} \mathrm{ms}^{-1}\right)^{2} \times 8.5 \times 10^{3} \times 3.09 \times 10^{16} \mathrm{mpc}^{-1} /\left(6.673 \times 10^{-11} \mathrm{Nm}^{2} \mathrm{~kg}^{-2}\right) \\ =1.905 \times 10^{41} \mathrm{~m}^{2} \mathrm{~s}^{-2} \mathrm{mN}^{-1} \mathrm{~m}^{-2} \mathrm{~kg}^{2} \\ =1.905 \times 10^{41} \mathrm{~m}^{3} \mathrm{~s}^{-2}\left(\mathrm{kgms}^{-2}\right)^{-1} \mathrm{~m}^{-2} \mathrm{~kg}^{2} \\ M_{\mathrm{mw}}=1.905 \times 10^{41} \mathrm{~kg} \end{array}$$

از آنجا که جرم خورشید برابر با $$M_{\odot}=1.99 \times 10^{30} \mathrm{~kg}$$ است برای جرم کهکشان راه شیری در فاصله $$8.5\ kpc$$ داریم:

$$\begin{aligned} M_{M w}(8.5 k p c) &=1.905 \times 10^{41} \mathrm{~kg} / 1.99 \times 10^{30} \mathrm{kgM}_{\odot}^{-1} \\ &=9.6 \times 10^{10} \mathrm{M}_{\odot} \end{aligned}$$

(ب) ممکن است بپرسيد که نتیجه به دست آمده چه قدر با واقعیت همخوانی دارد؟ زیرا ما می‌دانیم که جرم درون راه شیری به صورت کروی و متقارن توزیع نشده است با این حال ما در حل این سوال از این فرض استفاده کردیم که نوع توزیع جرم از حیث کروی متقارن است. با در نظر گرفتن اين موضوع می‌توان پاسخ را به شکل زير گرد کرد و داریم:

$$M_{\operatorname{mw}}(8.5 \mathrm{kpc})=1 \times 10^{11} M_{\odot}$$

استفاده از منحنی چرخش

پاسخ به سوال بالا نشان می‌دهد جرم بخش داخلی مدار گردش خورشید که $$8.5\ kpc$$ با مرکز راه شیری فاصله دارد در حدود $$10^{11} M_{\odot}$$ است. اگر بخواهیم کل جرم کهکشان راه شیری را بیابیم باید لبه‌های خارجی این کهکشان را نیز مورد مطالعه قرار دهیم به نوعی که تمام اجسام موجود در کهکشان راه شیری در محاسبات وارد شوند.

این مطالعه تنها به دلیل پیچیدگی تعیین مرزهای دقیق راه شیری دشوار نیست بلکه حتی اگر ما تصور کنیم در ورای یک شعاع معین دیگر ماده قابل رویت چندانی وجود ندارد، بازهم نمی‌توانیم مطمئن باشیم که لبه ماده تاریکی که مربوط به کهکشان راه شيری است را یافته‌ایم.

در این حالت ترسیم منحنی چرخش می‌تواند پاسخ به این پرسش که راه شیری کجا تمام می شود را روشن‌تر کند. ما در پاسخ به سوال بالا دریافتیم که چگونه می‌توان جرم داخلی راه شیری در یک شعاع مشخص را با دانستن سرعت گردش در مدار آن نقطه محاسبه کرد.

با استفاده از داده‌های رصدی حاصل از منحنی چرخش اجسام می‌توان جرم $$M(r)$$ را در تمام بازه‌های شعاعی محاسبه نمود و با انجام این کار مشخص می‌شود چگونه $$M(r)$$ با شعاع افزایش می‌یابد و از اين راه می‌توان میزان پراکندگی اجرام را بدست آورد.

با ملاحظه چگونگی تغییر توزيع جرم در خارجی‌ترین بخش‌های قابل اندازه‌گیری راه شیری، می‌توان مشاهده كرد كه در آخرين نقاط اندازه‌گيری شده توزيع جرم روند نزولی دارد.

روش معمول برای اندازه‌گیری $$M(r)$$ در یک کهکشان بدین صورت است:

1. ابتدا یک فرض منطقی برای حد پراکندگی اجرام در کهکشان را با توجه به داده‌های رصدی برآورد می‌کنیم.
2. سپس منحنی چرخشی که چنین پراکندگی را ایجاد می‌کند به دست می‌آوریم.
3. در مرحله بعد حدس اولیه را تا زمانی که منحنی چرخش رسم شده با منحنی چرخش رصد شده تطبیق پیدا کند تعدیل می‌کنیم.

برای درک بیشتر این فرآیند سوال زیر را بررسی خواهیم کرد که در آن منحنی چرخش برای توزیع جرمی جسمی ساده و فرضی محاسبه شده و سپس از این نتایج برای تفسیر داده‌های رصدی یعنی شکل‌های تصویر (۱) استفاده می‌کنیم.

پرسش: با استفاده از رابطه منحنی چرخش توزیع جرم جسمی که در آن $$M(r)=M$$ است را به دست آورید.

پاسخ: منحنی چرخش در واقع نسبت سرعت به شعاع است بنابراین شکل مناسب‌تر رابطه منحنی چرخش عبارت از $$v=(\frac{GM(r)}{r})^{\frac{1}{2}}$$ است. برای ترسیم منحنی چرخش باید بدانيم كه سرعت چگونه با شعاع تغيير می‌كند. از آنجا که در این مثال $$M(r)$$ یک مقدار ثابت است رابطه برای سرعت به شکل زیر نوشته می‌شود و داریم:

$$v(r)=(G M / r)^{1 / 2}=\text { const } \times 1 / r^{1 / 2}$$

رابطه فوق نشان می‌دهد که منحنی چرخش با افزایش شعاع کاهش می‌یابد و بنابراین در ترسیم منحنی چرخش در این مورد بايد منحنی با سرعتی كه شعاع افزايش می‌يابد، كاهش پيدا كند و در شعاع‌های بزرگ برابر با مقداری ثابت شود.

یک مثال از یک سیستم تحت کنترل یک جرم میانی، منظومه شمسی است. بنابراین نمودار گردش باید با شکل دوم تصویر (۱) مطابقت داشته باشد.

به لحاظ تاریخی «یوهانس کپلر» (Johannes Kepler) (1630-1571) بود که برای اولین بار تشخیص داد چنین رابطه‌ای حرکت سیارات در منظومه شمسی را توصیف می‌کند. از این جهت منجمین در حال حاضر برای توصیف حرکت یک جسم تحت تأثیر جاذبه یک جسم بسیار سنگين‌تر از واژه مدار کپلری استفاده می‌کنند.

شکل سوم تصویر (۱)، داده‌های رصدی مربوط به منحنی چرخش را برای راه شیری نمایش می‌دهد. برخی از خصوصیات این شکل مانند اوج در نزدیک مرکز راه شیری و کاهش شدید پس از آن بیشتر به سبب نادرست بودن فرض تقارن است و بيش از آنكه خصوصيات واقعی نمودار چرخش را نشان دهد متكی بر تحليل است.

البته تصور می شود ثابت بودن منحنی چرخش در فاصله‌های دور از مركز راه شيری واقعی باشد. زیرا همین ثابت بودن منحنی چرخش است که مشاهده لبه دیسک کهکشانی را ممکن می‌سازد و مستنداتی از حضور مقدار قابل توجهی از ماده غیر درخشان در اطراف راه شیری، یعنی ماده تاریک را ارائه می‌دهد.

اگر منحنی سرعت چرخش برای راه شیری، به غیر از چند پارسک اولیه نزدیک به مرکز را (شکل سوم تصویر ۱) با منحنی چرخش جسمی که به صورت $$M(r)=kr$$ توزیع شده مقایسه کنید، متوجه می‌شوید که تغییرات سرعت هر دو تقریباً یکسان و ثابت است. یعنی در هر دو حالت با افزایش فاصله از مرکز سرعت تغییری نمی‌کند.

یعنی در حالتی که جرم جسم برابر با $$M(r)=kr$$ باشد، رابطه سرعت و فاصله به صورت زیر به دست می‌آید:

$$v=(\frac{Gkr}{r})^{\frac{1}{2}}=const$$

در این حالت سرعت چرخش اجسام به فاصله تا مرکز بستگی ندارد و نمودار به صورت یک خط با شیب صفر به دست می‌آید. این نمودار می‌تواند شبیه به شکل سوم تصویر (۱) باشد.

اگر بیشتر جرم راه شیری درون بزرگترین شعاع اندازه‌گیری شده قرار گیرد باید انتظار داشت كه منحنی چرخش با افزایش فاصله شعاعی به شکلی کاملاً سریع کاهش پیدا کند، همانگونه که در مورد حالت $$M(r)=M$$ اتفاق افتاد. بدین ترتیب پاسخ به این سوال که جرم راه شیری چه قدر است، بستگی به جواب سوال دیگری خواهد داشت و آن این است که کجا منحنی چرخش حركت نزولی خود را آغاز می‌كند.

هنوز ابهامات فراوانی در مورد نحوه توزیع جرم در راه شیری وجود دارد. فرض‌های متفاوت در مورد شعاع راه شیری و نحوه توزیع ماده تاریک در آن، تخمین‌هایی در مورد مجموع جرم راه شیری به دست می‌دهد.

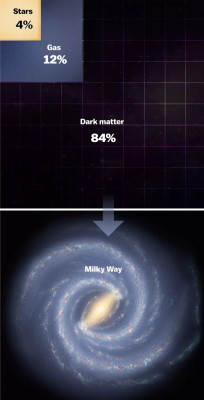
این تخمین‌ها از مقدار چهار برابر جرم ستاره‌ها یعنی $$4\times10^{11} M_{\odot}$$ تا مقدار قابل توجه 60 برابر جرم ستاره‌ها یعنی $$60\times10^{11} M_{\odot}$$ متغیر است. جرم راه شیری با استفاده از سرعت سایر اشیاء در مجاورت دیسک گازی مانند ستاره‌های دور از هاله ستاره‌ای یا خوشه‌های ستاره‌ای کروی و کهکشان های نزدیک نیز قابل تخمین زدن است اما این روش‌ها نیز بر فرضیات خاص استوار هستند و هنوز مسئله حل نشده است.

تعیین جرم کهکشان های مارپیچ از طریق نمودار گردش

در قسمت قبل توضیح دادیم که هنوز تردید بسیار زیادی در مورد جرم کهکشان راه شیری وجود دارد زیرا هنوز میزان ماده تاریک و یا نوع توزیع ماده در کهکشان راه شیری نامشخص است. با این حال در این قسمت می‌خواهیم از منحنی چرخش‌ برای تعیین جرم کهکشان‌های مارپیچی استفاده کنیم.

همان طور که گفتیم منحنی چرخش تغییرات سرعت بر حسب فاصله از مرکز کهکشانی را می‌دهد و برای تعیین جرم، سرعت چرخش رصدی را با سرعت چرخش تئوری مقایسه می‌کنیم. در این حالت توزیع جرم نظری تصحیح می‌شود تا بین نمودار رصد شده و نمودار پیش‌بینی شده بر اساس مدل‌ها همخوانی حاصل شود. جرم مجموع در مدل نهایی (شامل ماده تاریک) بیانگر جرم صحیح یک کهکشان است.

این روش با مشکلات گوناگونی روبه رو است از جمله این واقعیت که (با توجه به فرض تقارن که این روش به آن متکی است) این روش برای کهکشان‌های مارپیچی که بار مرکزی دارند مناسب نیست. به علاوه این روش تنها حد پایین جرم کهکشان‌ها را در اختیار می‌گذارد. هم چنین این روش  به دانستن فاصله شعاعی یعنی $$r$$ بستگی دارد که برای آن دانستن فاصله تا کهکشان لازم است. با این وجود، این روش نسبتاً آسان است و به شکل گسترده‌ای مورد استفاده قرار می‌گیرد.

پرسش: چرا این روش تنها حد پایین جرم کهکشان را در اختیار می‌گذارد؟

پاسخ: زیرا این روش تنها برای جرم داخلی تا مرکز یک شعاع مشخص $$r$$ که نمودار گردش برای آن اندازه‌گیری شده است کاربرد دارد.

برای اطمینان از اینکه رصدها برای نمودار گردش تا بیشترین حد ممکن مقدار $$r$$ انجام شده باشد، متداول است که رصدها را بر مبنای تغییر مکان دوپلری تابش 21 سانتی‌متر که از هیدروژن خنثی متصاعد می‌شود، انجام می‌دهند.

ولی این تابش هیدروژن چیست و چه چیزی را نشان می‌دهد؟ با فرض توزیع یکنواخت اتم‌های هیدروژن در کهکشان هر خط دید از یک کهکشان معادل یک خط هیدروژن است. تنها تفاوت هر یک از این خطوط در جابه‌جایی دوپلر است که هر یک از این خطوط دارند. از این رو با این تفاوت می‌توان سرعت نسبی هر بازوی کهکشان راه شیری را محاسبه کرد.

در کهکشان های نزدیک، تابش 21 سانتی‌متر هیدروژن معمولاً به سادگی در آنسوی محدوده دیداری دیسک نیز قابل ردیابی است. (ماده تاریک از این محدوده نیز فراتر می‌رود) مثالی از نقشه تغییر مکان داپلری برای کهکشان M81 با استفاده از رنگ‌ها، در تصویر (۲) نمایش داده شده است.

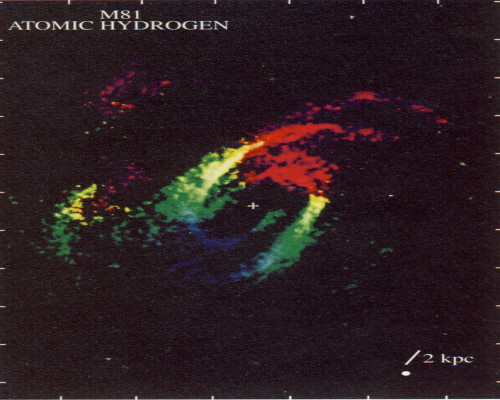
البته اندازه‌گیری تغییر مکان داپلری تنها سرعت اجزای در امتداد خط دید را مشخص می‌کند و لذا برای استخراج نمودار گردش کهکشان از داده‌های به دست آمده از تصویر (۲) ضروری است جهت‌گیری کهکشان نسبت به ناظر نیز در نظر گرفته شود. نمودار سرعت چرخش که از این طریق برای کهکشان M81 و چند کهکشان دیگر استخراج شده در تصویر (۳) نمایش داده شده است.

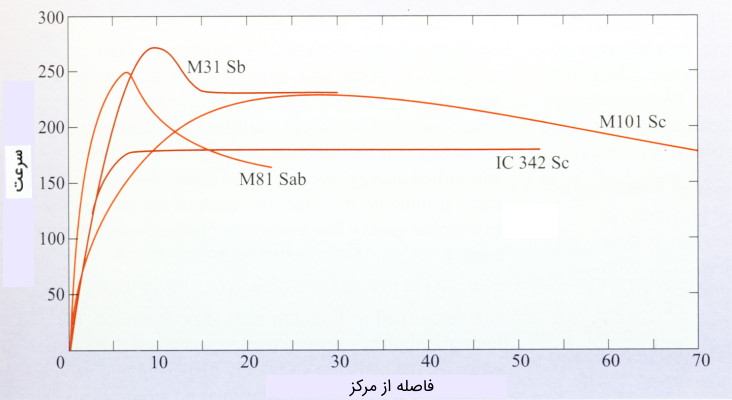
برای کهکشان‌های دورتر ممکن است وضوح اندازه‌گیری 21 سانتی‌متر آنقدر پایین باشد که نتوان آن را بر اساس تغییر مکان داپلری در موقعیت‌های مختلف دیسک ترسیم نمود.

دلیل موضوع این است که این خط مجموع تمام تابش‌های 21 سانتی‌‏متری از گازها در تمام بخش‌های کهکشان را نشان می‌دهد و به دليل تغییر مکان‌های داپلری متفاوت از بخش‌های متفاوت این خط پهن می‌شود. در این حالت تعیین نمودار گردش از چنین اندازه‌گیری ممکن نیست، اما بالاترین سرعت گردش هر دیسک قابل پیدا کردن است و از این مقدار تخمین جرم کهکشان ممکن خواهد بود.

صرف نظر از محدوديت‌های موجود اندازه گیری‌های 21 سانتی‌متر، نمودار گردش و تعیین جرم کهکشان مسائل بسیار مهمی در ستاره شناسی مدرن هستند و شواهدی از توزیع جرم کهکشان ها خارج از محدوده قابل رویت دیسک در اختیار می‌گذارند و بخش مهمی از دانسته‌های امروز ما در مورد ماده تاریک را در اختیارمان گذاشته‌اند.

تعیین جرم کهکشان های بیضوی توسط پراکندگی سرعت 

گردش (حرکت منظم در یک صفحه پیرامون مرکز کهکشان) در کهکشان های بیضوی شکل نسبتاً بی‌ اهمیت است. این کهکشان ها را اغلب به مانند یک توده ستاره‌ای ساده متشکل از تعداد زیادی ستاره که برای مدت طولانی در کنار هم درون مدار کهکشانی تحت تاثیر جاذبه‌ یکدیگر باقی مانده‌اند در نظر می‌گیرند.

اگر این دیدگاه صحیح باشد، محاسبه كميتي که پراکندگی سرعت نامیده می‌شود ($$\Delta v$$) برای یک کهکشان بیضی شکل ممکن خواهد بود. پراکندگی سرعت یک کمیت آماری است که دامنه سرعت‌های ستاره‌ها را در امتداد خط دید مشخص می‌سازد.

در یک کهکشان بیضی شکل پراکندگی سرعت از رابطه $$(\frac{M}{R})^{\frac{1}{2}}$$ به دست می‌آيد که در آن $$M$$ جرم کهکشان و $$R$$ مقیاس طولی مربوط به اندازه آن است.

این رابطه از قضیه ویریال به دست می‌‌آید و می‌توان آن را برای یک کهکشان بیضی شکل که اندازه $$R$$ در آن مشخص است و مقدار $$\Delta v$$ را نیز در آن می‌توان از اندازه‌گیری تغییر مکان داپلری تخمین زد به کار برد. این رابطه مقدار منطقی برای جرم در اختیار خواهد گذاشت اما باید توجه داشت، جرم بدست آمده از این رابطه تنها حد پایینی جرم کهکشان را معین می‌کند.

قضیه ویریال

قضیه ویریال، مجموع انرژی پتانسیل گرانشی یک کهکشان را به حاصل جمع انرژی‌های جنبشی تمام اجزای منفرد که آن کهکشان را می‏‌سازند مرتبط می‌کند.

قضیه ویریال برای هر سیستمی شامل اجزای متفاوت که در آن جاذبه گرانشی حاکم بوده قابل استفاده است و کهکشان ها چنین سیستم‌هایی هستند. اما این قضیه در موارد کوچکتر مانند خوشه‌های ستاره‌ای و نیز موارد بسیار بزرگتر مانند مجموعه‌های کهکشانی نيز کاربرد دارد.

در این جا ما کهکشان ایده‌آل را در نظر می‌گیریم که تنها از ستاره تشکیل شده است (یعنی از هر جزء دیگری که ممکن است در یک کهکشان واقعی وجود داشته باشد صرف‌نظر می‌کنیم). مجموع انرژی جنبشی برای کل سیستم $$E_{K}$$ عبارت از حاصل جمع انرژی هر ستاره است.

هم چنین انرژی پتانسیل گرانشی آن از بر هم کنش گرانشی آن ستاره با تمام ستاره‌های دیگر کهکشان حاصل می‌شوند. این انرژی پتانسیل گرانشی $$-1$$ برابر انرژی لازم برای فرار ستاره از این کهکشان است.

انرژی پتانسیل گرانشی هر ستاره کمیتی منفی است زیرا بر اساس قرارداد، انرژی پتانسیل گرانشی یک ستاره هنگامی که این ستاره بسیار دور از کهکشان باشد به سمت صفر می‌رود و در این حالت از کشش گرانشی کهکشان آزاد است.

از آنجا که هر ستاره باید مقدار مثبتی از انرژی داشته باشد تا قادر به رسیدن به حالت صفر انرژی باشد، در این حالت هر ستاره در کهکشان انرژی پتانسیل جاذبه‌ای منفی خواهد داشت.

مجموع انرژی پتانسیل گرانشی $$E_{g}$$ برای یک کهکشان را می‌توان به شکل مشابهی تعریف کرد. براساس قرارداد مجموع انرژی پتانسیل گرانشی هنگامی که تمامی ستاره‌ها کاملاً پراکنده باشند و جاذبه یکی بر دیگری تاثیر نداشته باشد به سمت صفر میل می‌كند.

اگر فرآیندی که در آن ستاره‌ها یکی پس از دیگری از جاذبه کهکشان رها می‌شوند را در نظر بگیریم، واضح است که باید مقدار مثبتی از انرژی وجود داشته باشد تا بتوان به حالت صفر انرژی پتانسیل گرانشی رسید. بنابراین مجموع انرژی پتانسیل گرانشی مقدار منفی این انرژی جداسازی خواهد بود.

در حالتی از قضیه ویریال که در آن کهکشان در حالت پایدار قرار می‌گیرد (حالتی که کهکشان نه منقبض می‌شود و نه منبسط) مجموع انرژی جنبشی و انرژی پتانسیل گرانشی از طریق رابطه زیر به هم مربوط می‌شوند:

$$E_k=-\frac{1}{2}E_g$$

از اثبات این رابطه در این جا صرف نظر می‌کنیم اما دو نتیجه مفید این رابطه را شرح خواهیم داد:

1. علامت منفی قابل پیش بینی است زیرا مجموع انرژی جنبشی مثبت خواهد بود، در حالیکه مجموع انرژی پتانسیل گرانشی باید منفی باشد.
2. انرژی جنبشی ستاره‌ها کمتر از مقدار انرژی است که برای جداسازی کامل اجزای کهکشان لازم است، چرا که اگر مجموع انرژی جنبشی برابر با انرژی پتانسیل گرانشی شود باعث پراکنده شدن کامل ستاره‌ها و از هم گسیختن کهکشان خواهد شد.

شرایطی که کهکشان در آن در حالت پایدار قرار می‌گیرد و منقبض و منبسط نمی‌شود حیاتی است. برای روشن شدن موضوع سیستمی از ستاره‌ها را در نظر بگیرید که به شکلی توزیع شده‌اند که یک ابر کروی یکنواخت تشکیل داده‌اند. هم چنین در نظر بگیرید تمام ستاره‌ها ساکن هستند. در این حالت مجموع انرژی جنبشی این سیستم چه قدر است؟

از آنجا که ستاره‌ها همگی ساکن هستند مجموع انرژی جنبشی صفر است و قضیه ویریال کابرد ندارد اما این حالت به شدت ناپایدار است. این سیستم هنگامی که هر ستاره تحت تاثیر جاذبه ستاره‌ای ديگر شتاب می‌گیرد شروع به فروپاشی می‌كند.  بنابراین مجموع انرژی جنبشی ستاره‌های دیگر افزایش می‌یابد.

به دلیل این که ستاره‌ها نسبتاً کوچک و کاملاً جدا از هم هستند به هم برخورد نمی‌کنند اما برخی از آن‌ها آنقدر به هم نزدیک می‌شوند که از مسیرشان منحرف شوند و در نتیجه انرژی پتانسیل و جنبشی می‌توانند به يكديگر تبديل شوند.

مجموع انرژی سیستم در فرآیند فروپاشی ثابت باقی خواهد ماند اما کل سیستم شروع به انقباض خواهد کرد و انرژی پتانسیل گرانشی آن کاهش پیدا می‌کند (منفی‌تر خواهد شد). لذا با کاهش انرژی پتانسیل، انرژی جنبشی ستاره‌ها افزایش خواهد یافت. در نهایت سیستم به حالتی خواهد رسید که پایدار می‌شود (نه منقبض می‌شود نه منبسط) و مجموع انرژی به شکلی که در رابطه بالا نشان داده شده است بین انرژی جنبشی و پتانسیل تقسیم خواهد شد و قضیه ویریال برای سیستم قابل استفاده است.

باید توجه داشت که قضیه ویریال در مورد سیستم‌های متشکل از اجزای متفاوت که تنها در اثر جاذبه بر هم کنش دارند قابل استفاده است بنابراین این قضیه را می‌توان در مورد کهکشان‌ های مارپیچ نیز به کار برد.

تعیین جرم هاله‌های کهکشان های بیضوی توسط پرتو ایکس

برخی کهکشان‌های بیضی شکل درخشان، هاله‌ای از گاز داغ و پخش شده با دمایی در حدود چندین میلیون درجه کلوین دارند. رصدهای پرتو ایکس از این کهکشان‌ها، حد دما و چگالی این هاله‌های گازی را معین می‌کند.

تکنیک اندازه‌گیری جرم بر این فرض استوار است که این هاله‌های داغ گازی مقید به کهکشان مربوطه هستند. به شکل کلی با معلوم بودن حد و دمای هاله، جرم آن قابل اندازه‌گیری خواهد بود. وجود هاله بسیار داغ و بزرگ به معنای جرم زیاد کهکشان است که اجازه فرار از هاله را نمی‌دهد.

برای اندازه‌گیری جرم در این حالت اندازه‌های به دست آمده از پرتو ایکس با مدل تئوریک هاله گازی مقایسه می‌‏شود و جرم کهکشان از طریق این مقایسه به دست می‌آید.

از این روش برای محاسبه جرم کهکشان های بیضی شکل غول پیکر و همچنین با اصول مشابه برای محاسبه جرم مجموعه‌های کهکشانی استفاده می‌شود. همچنین اندازه‌گیری پرتو ایکس از کهکشان‌های بیضی شکل نشان‌دهنده وجود مقدار قابل توجهی ماده (عمدتاً هیدروژن) است. این ماده رویت شده چیزی فراتر از موادی است که در طول موج قابل رؤیت، پرتو هیدروژن ساطع می‌کنند.

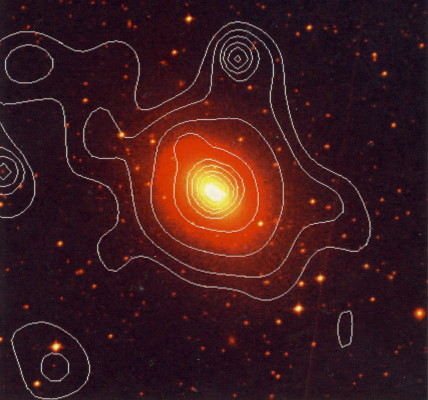
در شکل بالا تصویر به دست آمده از طریق پرتو ایکس و روش اپتیکی برای کهکشان بیضی شکل NGC 3923 روی هم قرار گرفته‌اند. گاز داغ و پراکنده شده که توسط تابش پرتو ایکس ردیابی شده، به شکل واضحی از ابعاد تصویر اپتیکی فراتر رفته است.

جمع‌بندی

در این مطلب در مورد تعیین جرم کهکشان‌ها صحبت کردیم و سه روش برای تعیین جرم این اجرام آسمانی معرفی شد. همچنین دلیل عدم قطعیت در مورد نتایج و تفاوت در جواب‌های به دست آمده را توضیح دادیم. به علاوه جرم کهکشان راه شیری را محاسبه کردیم و در ادامه در مورد روش‌های مورد استفاده برای تعیین جرم یک کهکشان مارپیچ و بیضوی سخن گفتیم.