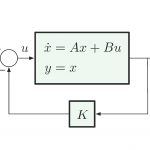
در آموزشهای قبلی مجله فرادرس، با نمایش فضای حالت سیستمهای دینامیکی و حل معادله حالت آشنا شدیم و دیدیم که فضای حالت، نمایشی از دورن سیستم را ارائه میکند. در این آموزش، با یکی از مفاهیم طراحی سیستم کنترل به نام تحقق فضای حالت آشنا میشویم که تابع تبدیل را به فرم مورد نظر در فضای حالت بیان میکند.
مدل سیستم در فضای حالت
مدل کلی فضای حالت یک سیستم خطی تغییر ناپذیر با زمان را با بردار حالت x x x u u u y y y
x ˙ = A x + B u , y = C x + D u , \large \begin{align*} \dot{x} &= Ax + Bu, \\ y &= Cx + Du, \end{align*} x ˙ y = A x + B u , = C x + D u ,
که در آن:
x = ( x 1 ⋮ x n ) ∈ R n , u = ( u 1 ⋮ u m ) ∈ R m , y = ( y 1 ⋮ y p ) ∈ R p . \large \begin{align*} x = \left ( \begin {matrix} x _ 1 \\ \vdots \\ x _ n \end {matrix} \right ) \in \mathscr {R} ^ n, \, \,\,\,\,\,\, u = \left ( \begin {matrix} u _ 1 \\ \vdots \\ u _ m \end {matrix} \right ) \in \mathscr { R } ^ m , \,\,\,\,\,\,\, y = \left ( \begin {matrix} y _ 1 \\ \vdots \\ y _ p \end {matrix} \right ) \in \mathscr { R } ^ p . \end{align*} x = x 1 ⋮ x n ∈ R n , u = u 1 ⋮ u m ∈ R m , y = y 1 ⋮ y p ∈ R p .
همچنین:
A A A n × n n \times n n × n B B B n × m n \times m n × m C C C p × n p \times n p × n و D D D p × m p \times m p × m
تبدیل فضای حالت به تابع تبدیل
در این بخش میخواهیم شیوه به دست آوردن تابع تبدیل از u u u y y y
x ˙ = A x + B u , y = C x + D u . \large \begin {align*} \dot { x } & = A x + B u , \\ y & = C x + D u . \end {align*} x ˙ y = A x + B u , = C x + D u .
وضعیتی را در نظر میگیریم که متغیرهای ورودی، حاالت و خروجی اسکالر باشند (x , y , u ∈ R x,y,u \in \mathscr {R} x , y , u ∈ R تبدیل لاپلاس استفاده کرده و آن را بر معادلات اعمال میکنیم. روند مشابهی را برای کار با بردارها طی میکنیم. ضرب ماتریس-بردار زیر را در نظر بگیرید:
x ˙ i = ( A x ) i + ( B u ) i = ∑ j = 1 n a i j x j + ∑ k = 1 m b i k u k , ( 1 ) y ℓ = ( C x ) ℓ + ( D u ) ℓ = ∑ j = 1 n c ℓ j x j + ∑ k = 1 m d ℓ k u k . ( 2 ) \large \begin {align*} \dot { x } _ i & = ( A x ) _ i + ( B u ) _ i \\ \ & = \sum ^ n _ { j = 1 } a_ { i j } x _ j + \sum ^ m _ { k = 1 } b _ { i k } u _ k , \; \; \; \; \; (1)\\ y _ \ell & = ( C x ) _ \ell + ( D u ) _ \ell \\ & = \sum ^ n _ { j = 1 } c _ { \ell j } x _ j + \sum ^ m _ { k = 1 } d _ { \ell k } u _ k . \; \; \; \; \; (2) \end{align*} x ˙ i y ℓ = ( A x ) i + ( B u ) i = j = 1 ∑ n a ij x j + k = 1 ∑ m b ik u k , ( 1 ) = ( C x ) ℓ + ( D u ) ℓ = j = 1 ∑ n c ℓ j x j + k = 1 ∑ m d ℓ k u k . ( 2 )
اگر از هر دو طرف معادله (۱) تبدیل لاپلاس بگیریم، داریم:
x ˙ i = ∑ j = 1 n a i j x j + ∑ k = 1 m b i k u k ↓ L s X i ( s ) − x i ( 0 ) = ∑ j = 1 n a i j X j ( s ) + ∑ k = 1 m b i k U k ( s ) , ∀ i = 1 , … , n . \large \begin {align*} \dot { x } _ i & = \sum ^ n _ { j= 1 } a _ { i j } x _ j + \sum ^ m _ { k = 1 } b _ { i k } u _ k \\ & \qquad \qquad \downarrow {\mathscr L} \\ s X _ i ( s ) - x _ i ( 0 ) & = \sum ^ n _ { j = 1 } a _ { i j } X _ j ( s ) + \sum ^ m _ { k = 1 } b _ { i k } U _ k ( s ) , \forall ~ i = 1 , \ldots , n . \end{align*} x ˙ i s X i ( s ) − x i ( 0 ) = j = 1 ∑ n a ij x j + k = 1 ∑ m b ik u k ↓ L = j = 1 ∑ n a ij X j ( s ) + k = 1 ∑ m b ik U k ( s ) , ∀ i = 1 , … , n .
با مرتب کردن n n n
s X ( s ) − x ( 0 ) = A X ( s ) + B U ( s ) ( s I − A ) X ( s ) = x ( 0 ) + B U ( s ) ⟹ X ( s ) = ( s I − A ) − 1 x ( 0 ) + ( s I − A ) − 1 B U ( s ) , \large \begin {align*} s X ( s ) - x ( 0 ) & = A X ( s ) + B U ( s ) \\ ( s I - A ) X ( s ) & = x ( 0 ) + B U ( s ) \\ \implies X ( s ) & = ( s I - A ) ^ { - 1 } x ( 0 ) + ( s I -A ) ^ { - 1 } B U ( s ) , \end {align*} s X ( s ) − x ( 0 ) ( s I − A ) X ( s ) ⟹ X ( s ) = A X ( s ) + B U ( s ) = x ( 0 ) + B U ( s ) = ( s I − A ) − 1 x ( 0 ) + ( s I − A ) − 1 B U ( s ) ,
که در آن، I I I n × n n \times n n × n
به طریق مشابه و با اعمال تبدیل لاپلاس بر معادله (۲)، داریم:
y ℓ = ∑ j = 1 n c ℓ j x j + ∑ k = 1 m d ℓ k u k ↓ L Y ℓ ( s ) = ∑ j = 1 n c ℓ j X j ( s ) + ∑ k = 1 m d ℓ k U k ( s ) , ∀ ℓ = 1 , … , p . \large \begin {align*} y _ \ell & = \sum ^ n _ { j = 1 } c _ { \ell j } x _ j + \sum ^ m _ { k = 1 } d _ { \ell k } u _ k \\ & \qquad \qquad \downarrow { \mathscr L } \\ Y _ \ell ( s ) & = \sum ^ n _ { j = 1 } c _ { \ell j } X _ j ( s ) + \sum ^ m _ { k = 1 } d _ { \ell k } U _ k ( s ) , \forall ~ \ell = 1 , \ldots , p . \end {align*} y ℓ Y ℓ ( s ) = j = 1 ∑ n c ℓ j x j + k = 1 ∑ m d ℓ k u k ↓ L = j = 1 ∑ n c ℓ j X j ( s ) + k = 1 ∑ m d ℓ k U k ( s ) , ∀ ℓ = 1 , … , p .
با مرتب کردن p p p
Y ( s ) = C X ( s ) + D U ( s ) = C [ ( s I − A ) − 1 x ( 0 ) + ( s I − A ) − 1 B U ( s ) ] + D U ( s ) = C ( s I − A ) − 1 x ( 0 ) + [ C ( s I − A ) − 1 B + D ] U ( s ) . \large \begin {align*} Y ( s ) & = C X ( s ) + D U ( s ) \\ & = C \left [ ( s I - A ) ^ { - 1 } x ( 0 ) + ( s I -A ) ^ { - 1 } B U ( s) \right ] + D U ( s ) \\ & = C ( s I - A ) ^ { - 1 } x ( 0 ) + \left [ C ( s I - A ) ^ { - 1 } B + D \right ] U ( s ) . \end {align*} Y ( s ) = CX ( s ) + D U ( s ) = C [ ( s I − A ) − 1 x ( 0 ) + ( s I − A ) − 1 B U ( s ) ] + D U ( s ) = C ( s I − A ) − 1 x ( 0 ) + [ C ( s I − A ) − 1 B + D ] U ( s ) .
برای به دست آوردن رابطه ورودی-خروجی یا همان تابع تبدیل، شرایط اولیه را برابر با 0 0 0
Y ( s ) = G ( s ) U ( s ) , G ( s ) = C ( s I − A ) − 1 B + D \large \begin{align*} Y ( s ) & = G ( s ) U ( s ) , \, \, \, \, \, \text { } G ( s ) = C ( s I - A ) ^ { - 1 } B + D \end {align*} Y ( s ) = G ( s ) U ( s ) , G ( s ) = C ( s I − A ) − 1 B + D
بنابراین، تابع تبدیل u u u y y y ( A , B , C , D ) (A,B,C,D) ( A , B , C , D )
G ( s ) = C ( I s − A ) − 1 B + D . ( 3 ) \large G ( s ) = C ( I s - A ) ^ { - 1 } B + D . \; \; \; \; \; (3) G ( s ) = C ( I s − A ) − 1 B + D . ( 3 )
همانطور که میبینیم، G ( s ) G(s) G ( s )
نکته ۱: اگر ماتریس s I − A sI-A s I − A منفرد و در نتیجه، معکوس ناپذیر باشد (یعنی det ( s I − A ) = 0 \det(sI-A) = 0 det ( s I − A ) = 0 G ( s ) G (s) G ( s )
نکته ۲: A A A n × n n \times n n × n det ( s I − A ) \det(sI-A) det ( s I − A ) n n n A A A
det ( s I − A ) = det ( s − a 11 − a 12 … − a 1 n − a 21 s − a 22 … − a 2 n ⋮ ⋮ ⋱ ⋮ − a n 1 − a n 2 … s − a n n ) \large \det ( s I - A ) = \det \left ( \begin {matrix} s - a _ { 1 1 } & - a _ { 1 2 } & \ldots & - a _ { 1 n } \\ - a _ { 2 1 } & s - a _ { 2 2 } & \ldots & - a _ { 2 n } \\ \vdots & \vdots & \ddots & \vdots \\ - a _ { n 1 } & - a _ { n 2 } & \ldots & s - a _ { n n } \end {matrix} \right ) det ( s I − A ) = det s − a 11 − a 21 ⋮ − a n 1 − a 12 s − a 22 ⋮ − a n 2 … … ⋱ … − a 1 n − a 2 n ⋮ s − a nn
ریشههای چندجملهای مشخصه، مقادیر ویژه ماتریس A A A
نکته ۳: تابع تبدیل حلقه باز G ( s ) G(s) G ( s ) A A A
مثال ۱
مدل فضای حالت زیر را به فرم کانونی کنترل پذیر (در ادامه این فرم را توضیح خواهیم داد) در نظر بگیرید:
( x ˙ 1 x ˙ 2 ) = ( 0 1 − 6 − 5 ) ⏟ A ( x 1 x 2 ) + ( 0 1 ) ⏟ B u , y = ( 1 1 ) ⏟ C ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & 1 \\ - 6 & - 5 \end {matrix} \right ) } _ { A } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) } _ { B } u , \\ y & = \underbrace { \left ( \begin {matrix} 1 & 1 \end {matrix} \right ) } _ { C } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = A ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + B ( 0 1 ) u , = C ( 1 1 ) ( x 1 x 2 ) .
تابع تبدیل u u u y y y
حل: سیستم فوق، تکورودی-تکخروجی (SISO) با u , y ∈ R u , y \in \mathscr { R } u , y ∈ R x x x D = 0 D=0 D = 0 G ( s ) G (s) G ( s )
G ( s ) = C ( I s − A ) − 1 B , ( D = 0 ) s I − A = ( s − 1 6 s + 5 ) . ( 4 ) \large \begin{align*} G ( s ) & = C ( I s - A ) ^ { - 1 } B , \hspace {2.5cm} \text {($ D = 0 $)} \\ \text{ }\, s I - A & = \left ( \begin {matrix} s & - 1 \\ 6 & s + 5 \end {matrix} \right ) . \end{align*} \; \; \; \; \; (4) G ( s ) s I − A = C ( I s − A ) − 1 B , ( D = 0) = ( s 6 − 1 s + 5 ) . ( 4 )
برای محاسبه ( s I − A ) − 1 (sI-A)^{-1} ( s I − A ) − 1 معکوس ماتریس 2 × 2 2 \times 2 2 × 2
M = ( a b c d ) , det M ≠ 0 ⟹ M − 1 = 1 det M ( d − b − c a ) . \large \begin {align*} M = \left ( \begin {matrix} a & b \\ c & d \end{matrix} \right ) , \, \det M \neq 0 \quad \Longrightarrow \quad M ^ { - 1 } & = \frac { 1 } { \det M } \left ( \begin {matrix} d & - b \\ -c & a \end {matrix} \right ) . \end{align*} M = ( a c b d ) , det M = 0 ⟹ M − 1 = det M 1 ( d − c − b a ) .
با استفاده از فرمول بالا، داریم:
( s I − A ) − 1 = 1 det ( s I − A ) ( s + 5 1 − 6 s ) = 1 s 2 + 5 s + 6 ( s + 5 1 − 6 s ) . \large \begin {align*} ( s I - A ) ^ { - 1 } & = \frac { 1 } { \det ( s I - A ) } \left ( \begin {matrix} s + 5 & 1 \\ -6 & s \end {matrix} \right ) \\ & = \frac { 1 } { s ^ 2 + 5 s + 6 } \left ( \begin {matrix} s + 5 & 1 \\ -6 & s \end {matrix} \right ) . \end{align*} ( s I − A ) − 1 = det ( s I − A ) 1 ( s + 5 − 6 1 s ) = s 2 + 5 s + 6 1 ( s + 5 − 6 1 s ) .
اگر ماتریسهای B B B C C C G ( s ) G(s) G ( s )
G ( s ) = C ( s I − A ) − 1 B = ( 1 1 ) 1 s 2 + 5 s + 6 ( s + 5 1 − 6 s ) ( 0 1 ) = 1 s 2 + 5 s + 6 ( 1 1 ) ( 1 s ) = s + 1 s 2 + 5 s + 6 . \large \begin {align*} G ( s ) & = C ( s I - A ) ^ { - 1 } B \\ & = \left ( \begin {matrix} 1 & 1 \end {matrix} \right ) \frac { 1 } { s ^ 2 + 5 s + 6 } \left ( \begin {matrix} s + 5 & 1 \\ - 6 & s \end {matrix} \right ) \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) \\ & = \frac { 1 } { s ^ 2 + 5 s + 6 } \left ( \begin {matrix} 1 & 1 \end {matrix} \right ) \left ( \begin {matrix} 1 \\ s \end {matrix} \right ) \\ & = \frac { s + 1 } { s ^ 2 + 5 s + 6 } . \end{align*} G ( s ) = C ( s I − A ) − 1 B = ( 1 1 ) s 2 + 5 s + 6 1 ( s + 5 − 6 1 s ) ( 0 1 ) = s 2 + 5 s + 6 1 ( 1 1 ) ( 1 s ) = s 2 + 5 s + 6 s + 1 .
مدل فضای حالت این مثال، یک تحقق (Realization) از تابع تبدیل G ( s ) G(s) G ( s )
تحقق فضای حالت توابع تبدیل
در بخش قبل، تابع تبدیل را از مدل فضای حالت به دست آوردیم. در مقابل، میتوانیم مدل فضای حالت یک تابع تبدیل را تحقق بخشیم. برای توضیح این کار، از مثال بالا کمک میگیریم. تابع تبدیل مثال قبل را در نظر بگیرید:
G ( s ) = s + 1 s 2 + 5 s + 6 \large G ( s ) = \frac { s + 1 } { s ^ 2 + \color {red} { 5 } s + \color {blue} { 6 } } G ( s ) = s 2 + 5 s + 6 s + 1
مدل فضای حالتِ
( x ˙ 1 x ˙ 2 ) = ( 0 1 − 6 − 5 ) ⏟ A ( x 1 x 2 ) + ( 0 1 ) ⏟ B u , y = ( 1 1 ) ⏟ C ( x 1 x 2 ) \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & 1 \\ - \color {blue} { 6 } & - \color {red}{ 5 } \end {matrix} \right ) } _ { A } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) } _ { B } u , \\ y & = \underbrace { \left ( \begin {matrix} 1 & 1 \end {matrix} \right ) } _ { C } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) \\ \end{align*} ( x ˙ 1 x ˙ 2 ) y = A ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + B ( 0 1 ) u , = C ( 1 1 ) ( x 1 x 2 )
یک تحقق برای این تابع تبدیل است.
تحققهای دیگری نیز برای تابع تبدیل G ( s ) G(s) G ( s )
( x ˙ 1 x ˙ 2 ) = ( 0 1 − 6 − 5 ) ⏟ A ( x 1 x 2 ) + ( 0 1 ) ⏟ B u , y = ( 1 1 ) ⏟ C ( x 1 x 2 ) \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & 1 \\ - { 6 } & - { 5 } \end {matrix} \right ) } _ { A } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) } _ { B } u , \\ y & = \underbrace { \left ( \begin {matrix} 1 & 1 \end {matrix} \right ) } _ { C } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) \end {align*} ( x ˙ 1 x ˙ 2 ) y = A ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + B ( 0 1 ) u , = C ( 1 1 ) ( x 1 x 2 )
یه مدل فضای حالت جدید را با ترانهاده ماتریسهای A A A B B B C C C
x ˙ = A ˉ x + B ˉ u , y = C ˉ x , \large \begin {align*} \dot { x } & = \bar { A } x + \bar { B } u , \\ y & = \bar { C } x , \end {align*} x ˙ y = A ˉ x + B ˉ u , = C ˉ x ,
که در آن:
A ˉ = A T = ( 0 − 6 1 − 5 ) , B ˉ = C T = ( 1 1 ) , C ˉ = B T = ( 0 1 ) . \large \begin {align*} \bar { A } = A ^ T = \left ( \begin {matrix} 0 & -6 \\ 1 & - 5 \end {matrix} \right ) , \, \bar { B } = C ^ T = \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) , \, \bar { C } = B ^ T = \left ( \begin {matrix} 0 & 1 \end {matrix} \right ) . \end{align*} A ˉ = A T = ( 0 1 − 6 − 5 ) , B ˉ = C T = ( 1 1 ) , C ˉ = B T = ( 0 1 ) .
مدل بالا، یک مدل فضای حالت متفاوت از مدل نخست است و میتوان تابع تبدیل G ( s ) = C ˉ ( s I − A ˉ ) − 1 B ˉ G ( s ) = \bar { C } ( s I - \bar { A } ) ^ {- 1 } \bar { B } G ( s ) = C ˉ ( s I − A ˉ ) − 1 B ˉ
برای اثبات تحقق اخیر، مدل فضای حالت زیر را در نظر بگیرید:
x ˙ = A ˉ x + B ˉ u , y = C ˉ x , \large \begin {align*} \dot { x } & = \bar { A } x + \bar { B } u , \\ y & = \bar { C } x , \end {align*} x ˙ y = A ˉ x + B ˉ u , = C ˉ x ,
که در آن:
A ˉ = A T , B ˉ = C T , C ˉ = B T \large \begin {align*} \bar { A } = A ^ T , \, \bar { B } = C ^ T , \, \bar { C } = B ^ T \end{align*} A ˉ = A T , B ˉ = C T , C ˉ = B T
برای سیستم SISO، میتوان از رابطه تابع تبدیل به صورت زیر استفاده کرد:
C ˉ ( s I − A ˉ ) − 1 B ˉ = B T ( s I − A T ) − 1 C T = B T [ ( s I − A ) T ] − 1 C T = B T [ ( s I − A ) − 1 ] T C T = [ C ( s I − A ) − 1 B ] T = C ( s I − A ) − 1 B . \large \begin {align*} \bar { C } ( s I - \bar { A } ) ^ { - 1 } \bar { B } & = B ^ T \left ( s I - A ^ T \right ) ^ { - 1 } C ^ T \\ & = B ^ T \left [ ( s I - A ) ^ T \right ] ^ { - 1 } C ^ T \\ & = B ^ T \left [ \left ( s I - A \right ) ^ { - 1 } \right ] ^ T C ^ T \\ & = \left [ C ( s I - A ) ^ { - 1 } B \right ] ^ T \\ & = C ( s I - A ) ^ { - 1 } B . \end{align*} C ˉ ( s I − A ˉ ) − 1 B ˉ = B T ( s I − A T ) − 1 C T = B T [ ( s I − A ) T ] − 1 C T = B T [ ( s I − A ) − 1 ] T C T = [ C ( s I − A ) − 1 B ] T = C ( s I − A ) − 1 B .
بنابراین، مدل فضای حالت دوم، فرم کانونی مشاهده پذیر (OCF) نامیده میشود:
( x ˙ 1 x ˙ 2 ) = ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + ( 1 1 ) u , y = ( 0 1 ) ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \left ( \begin {matrix} 0 & -6 \\ 1 & - { 5 } \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) u , \\ y & = \left ( \begin {matrix} 0 & 1 \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end{align*} ( x ˙ 1 x ˙ 2 ) y = ( 0 1 − 6 − 5 ) ( x 1 x 2 ) + ( 1 1 ) u , = ( 0 1 ) ( x 1 x 2 ) .
تاکنون دو تحقق مختلف را به دست آوردیم. اکنون میخواهیم یک تحقق دیگر از G ( s ) = s + 1 s 2 + 5 s + 6 G(s) = \dfrac{s+1}{s^2+5s+6} G ( s ) = s 2 + 5 s + 6 s + 1 کسرهای جزئی آن به دست میآوریم:
G ( s ) = s + 1 ( s + 2 ) ( s + 3 ) = 2 s + 3 − 1 s + 2 . ( 5 ) \large \begin {align*} G ( s ) & = \frac { s + 1 } { ( s + 2 ) ( s + 3 ) } \\ & = \frac { 2 } { s + 3 } - \frac { 1 } { s + 2 } . \; \; \; \; \; (5) \end{align*} G ( s ) = ( s + 2 ) ( s + 3 ) s + 1 = s + 3 2 − s + 2 1 . ( 5 )
همانطور که میبینیم، معادله (۵)، G ( s ) G(s) G ( s )
این تحقق مدل فضای حالت، فرم کانونی مدال (MCF) نامیده میشود؛ زیرا مُدهای مختلف را مجزا یا دکوپله میکند (با مقادیر ویژه A A A
( x ˙ 1 x ˙ 2 ) = ( − 3 0 0 − 2 ) ( x 1 x 2 ) + ( 1 1 ) u , y = ( 2 − 1 ) ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \left ( \begin {matrix} - 3 & 0 \\ 0 & - { 2 } \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) u , \\ y & = \left ( \begin {matrix} 2 & - 1 \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end{align*} ( x ˙ 1 x ˙ 2 ) y = ( − 3 0 0 − 2 ) ( x 1 x 2 ) + ( 1 1 ) u , = ( 2 − 1 ) ( x 1 x 2 ) .
محاسبه تابع تبدیل از روی این مدل فضای حالت به صورت زیر است:
C ( I s − A ) − 1 B = ( 2 − 1 ) ( s + 3 0 0 s + 2 ) − 1 ( 1 1 ) = ( 2 − 1 ) ( 1 s + 3 0 0 1 s + 2 ) ( 1 1 ) = ( 2 − 1 ) ( 1 s + 3 1 s + 2 ) = 2 s + 3 − 1 s + 2 . \large \begin {align*} C ( I s - A ) ^ { - 1 } B & = \left ( \begin {matrix} 2 & - 1 \end {matrix} \right ) \left ( \begin {matrix} s + 3 & 0 \\ 0 & s + { 2 } \end {matrix} \right ) ^ { - 1 } \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) \\ & = \left ( \begin {matrix} 2 & -1 \end {matrix} \right ) \left ( \begin {matrix} \frac { 1 } { s + 3 } & 0 \\ 0 & \frac { 1 } { s + 2 } \end {matrix} \right ) \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) \\ & = \left ( \begin {matrix} 2 & - 1 \end {matrix} \right ) \left ( \begin {matrix} \frac { 1 } { s + 3 } \\ \frac { 1 } { s + 2 } \end {matrix} \right ) \\ & = \frac { 2 } { s + 3 } - \frac { 1 } { s + 2 } . \end{align*} C ( I s − A ) − 1 B = ( 2 − 1 ) ( s + 3 0 0 s + 2 ) − 1 ( 1 1 ) = ( 2 − 1 ) ( s + 3 1 0 0 s + 2 1 ) ( 1 1 ) = ( 2 − 1 ) ( s + 3 1 s + 2 1 ) = s + 3 2 − s + 2 1 .
از بحث بالا موارد زیر را نتیجه میگیریم:
تابع تبدیل G ( s ) G(s) G ( s )
ویژگیهای معین، مانند کنترل پذیری، مشاهده پذیری، مدال بودن و... برخی تحققها را نسبت به سایرین برتری میدهند.
ماتریس کنترل پذیری
سیستم تکورودی زیر را با u ∈ R u \in \mathscr {R} u ∈ R x ∈ R n x \in \mathscr {R}^n x ∈ R n
x ˙ = A x + B u , y = C x . \large \begin {align*} \dot { x } & = A x + B u , \\ y & = C x . \end {align*} x ˙ y = A x + B u , = C x .
ماتریس کنترل پذیری (Controllability) به صورت زیر تعریف میشود:
C ( A , B ) = [ B ∣ A B ∣ A 2 B ∣ … ∣ A n − 1 B ] . \large \begin {align*} { \cal C } ( A , B ) = \left [ B \, | \, A B \, | \, A ^ 2 B \, | \, \ldots \, | \, A ^ { n - 1 } B \right ] . \end{align*} C ( A , B ) = [ B ∣ A B ∣ A 2 B ∣ … ∣ A n − 1 B ] .
که در آن، A A A n × n n \times n n × n B B B n × 1 n \times 1 n × 1 C ( A , B ) {\cal C}(A,B) C ( A , B ) n × n n \times n n × n
سیستم بالا را کاملاً کنترل پذیر میگوییم، اگر ماتریس کنترل پذیری C ( A , B ) {\cal C}(A,B) C ( A , B )
تعریفی که گفته شد، فقط برای مواردی با یک ورودی صحیح است. برای سیستمی با چند ورودی، گفتههای مربوط به کنترل پذیری را برای رتبه (Rank) ماتریس کنترل پذیری C ( A , B ) {\cal C}(A,B) C ( A , B )
همانطور که در ادامه خواهیم دید، اگر سیستم کاملاً کنترل پذیر باشد، میتوان قطبهای حلقه بسته را با استفاده از کنترل کننده فیدبک حالت به فرم u = − K x u = - K x u = − K x
کنترل پذیر بودن سیستم با تعریفی که گفته شد، به تحقق فضای حالت بستگی دارد.
مثال ۲
ماتریس کنترل پذیری C ( A , B ) {\cal C}(A,B) C ( A , B )
( x ˙ 1 x ˙ 2 ) = ( 0 1 − 6 − 5 ) ⏟ A ( x 1 x 2 ) + ( 0 1 ) ⏟ B u , y = ( 1 1 ) ⏟ C ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & 1 \\ - { 6 } & -{ 5 } \end {matrix} \right ) } _ { A } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) } _ { B } u , \\ y & = \underbrace { \left ( \begin {matrix} 1 & 1 \end {matrix} \right ) } _ { C } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = A ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + B ( 0 1 ) u , = C ( 1 1 ) ( x 1 x 2 ) .
حل: با توجه به x ∈ R 2 x \in \mathscr {R}^2 x ∈ R 2 A ∈ R 2 × 2 A \in \mathscr {R}^{2 \times 2} A ∈ R 2 × 2 C ( A , B ) ∈ R 2 × 2 { \cal C } ( A , B ) \in \mathscr{R} ^ { 2 \times 2} C ( A , B ) ∈ R 2 × 2
ماتریس کنترل پذیری به صورت زیر است:
C ( A , B ) = [ B ∣ A B ] , A B = ( 0 1 − 6 − 5 ) ( 0 1 ) = ( 1 − 5 ) ⟹ C ( A , B ) = ( 0 1 1 − 5 ) . \large \begin {align*} { \cal C } ( A , B ) & = [ B \, | \, A B ] , \\ \text{ } \, A B & = \left ( \begin {matrix} 0 & 1 \\ - { 6 } & - { 5 } \end {matrix} \right ) \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) = \left ( \begin {matrix} 1 \\ - 5 \end {matrix} \right ) \\ \implies { \cal C } ( A , B ) & = \left ( \begin {matrix} 0 & 1 \\ 1 & - 5 \end {matrix} \right ) . \end {align*} C ( A , B ) A B ⟹ C ( A , B ) = [ B ∣ A B ] , = ( 0 − 6 1 − 5 ) ( 0 1 ) = ( 1 − 5 ) = ( 0 1 1 − 5 ) .
x ˙ = A x + B u , y = C x \large \begin {align*} \dot { x } & = A x + B u , \\ y & = C x \end {align*} x ˙ y = A x + B u , = C x
کنترل پذیری سیستم را با آزمایش معکوس پذیری C ( A , B ) \mathcal{C}(A, B) C ( A , B )
det C = − 1 ≠ 0 \large \begin{align*} \det {\cal C} = -1 \neq 0 \end{align*} det C = − 1 = 0
بنابراین، سیستم کاملاً کنترل پذیر است.
فرم کانونی کنترل پذیر
مدل فضای حالت تکورودی زیر را در نظر بگیرید:
x ˙ = A x + B u , y = C x \large \begin{align*} \dot{x} &= Ax + Bu, \\ y &= Cx \end{align*} x ˙ y = A x + B u , = C x
مدل فوق را فرم کانونی کنترل پذیر (Controller Canonical Form) یا CCF گویند، اگر ماتریسهای A A A B B B
A = ( 0 1 0 … 0 0 0 0 1 … 0 0 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 … 0 1 ∗ ∗ ∗ … ∗ ∗ ) , B = ( 0 0 ⋮ 0 1 ) \large \begin {align*} A & = \left ( \begin {matrix} 0 & 1 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 1 \\ * & * & * & \ldots & * & * \end {matrix} \right ) , \, B = \left ( \begin {matrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end {matrix} \right ) \end {align*} A = 0 0 ⋮ 0 ∗ 1 0 ⋮ 0 ∗ 0 1 ⋮ 0 ∗ … … ⋱ … … 0 0 ⋮ 0 ∗ 0 0 ⋮ 1 ∗ , B = 0 0 ⋮ 0 1
مدل فضای حالت CCF همواره کنترل پذیر است.
فرم کانونی کنترل پذیر با صفرهای دلخواه
تابع تبدیل مذکور G ( s ) = s + 1 s 2 + 5 s + 6 G(s) = \dfrac{s+1}{s^2 + 5s + 6} G ( s ) = s 2 + 5 s + 6 s + 1 z = − 1 z = -1 z = − 1 s = z s = z s = z
G ( s ) = s − z s 2 + 5 s + 6 . \large \begin {align*} G ( s ) = \frac { s - z } { s ^ 2 + 5 s + 6 } . \end {align*} G ( s ) = s 2 + 5 s + 6 s − z .
تحقق فرم کانونی کنترل پذیر، به صورت زیر خواهد بود:
( x ˙ 1 x ˙ 2 ) = ( 0 1 − 6 − 5 ) ⏟ A ( x 1 x 2 ) + ( 0 1 ) ⏟ B u , y = ( − z 1 ) ⏟ C ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & 1 \\ - { 6 } & -{ 5 } \end {matrix} \right ) } _ { A } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) } _ { B } u , \\ y & = \underbrace { \left ( \begin {matrix} - z & 1 \end {matrix} \right ) } _ { C } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = A ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + B ( 0 1 ) u , = C ( − z 1 ) ( x 1 x 2 ) .
از آنجایی که A A A B B B C C C
بنابراین میتوان گفت که مدل فضای حالت به فرم کانونی کنترل پذیر، بدون توجه به موقعیت صفرها، کنترل پذیر است.
فرم کانونی مشاهده پذیر با صفرهای دلخواه
در بخش قبل دیدیم که محل صفرهای یک سیستم به فرم کانونی کنترل پذیر، تأثیری بر کنترل پذیری آن ندارند و سیستمی به این فرم کاملاً کنترل پذیر است. دلیل این امر آن است که صفر در ماتریس کنترل پذیری وارد نمیشود. اما آیا این موضوع برای فرم کانونی مشاهده پذیر نیز صادق است؟
ابتدا مدل فضای حالت به فرم کانونی کنترل پذیر زیر را در نظر بگیرید:
( x ˙ 1 x ˙ 2 ) = ( 0 1 − 6 − 5 ) ⏟ A ( x 1 x 2 ) + ( 0 1 ) ⏟ B u y = ( − z 1 ) ⏟ C ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & 1 \\ - { 6 } & -{ 5 } \end {matrix} \right ) } _ { A } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} 0 \\ 1\end {matrix} \right ) } _ { B } u \\ y & = \underbrace { \left ( \begin {matrix} - z & 1 \end {matrix} \right ) } _ { C } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = A ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + B ( 0 1 ) u = C ( − z 1 ) ( x 1 x 2 ) .
با تبدیلاتِ
A ↦ A T , B ↦ C T , C ↦ B T \large A \mapsto A^T, B \mapsto C^T, C \mapsto B^T A ↦ A T , B ↦ C T , C ↦ B T
سیستم به فرم کانونی مشاهده پذیر زیر در میآید:
( x ˙ 1 x ˙ 2 ) = ( 0 − 6 1 − 5 ) ⏟ A ˉ = A T ( x 1 x 2 ) + ( − z 1 ) ⏟ B ˉ = C T u , y = ( 0 1 ) ⏟ C ˉ = B T ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \underbrace { \left ( \begin {matrix} 0 & - 6 \\ 1 & - { 5 } \end {matrix} \right ) } _ { \bar { A } \, =\, A ^ T } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \underbrace { \left ( \begin {matrix} - z \\ 1 \end {matrix} \right ) } _ { \bar { B } \, = \, C ^ T } u , \\ y & = \underbrace { \left ( \begin {matrix} 0 & 1 \end {matrix} \right ) } _ { \bar { C } \, = \, B ^ T } \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = A ˉ = A T ( 0 1 − 6 − 5 ) ( x 1 x 2 ) + B ˉ = C T ( − z 1 ) u , = C ˉ = B T ( 0 1 ) ( x 1 x 2 ) .
آیا این تحقق کاملاً کنترل پذیر است؟ برای پاسخ به این پرسش، ماتریس کنترل پذیری را تشکیل میدهیم:
C ( A ˉ , B ˉ ) = [ B ˉ ∣ A ˉ B ˉ ] , where A ˉ B ˉ = ( 0 − 6 1 − 5 ) ( − z 1 ) = ( − 6 − z − 5 ) ⟹ C ( A ˉ , B ˉ ) = ( − z − 6 1 − z − 5 ) . det C = z ( z + 5 ) + 6 = z 2 + 5 z + 6 = 0 for z = − 2 or z = − 3 . \large \begin {align*} { \cal C } ( \bar { A } , \bar { B } ) & = \left [ \begin {matrix} \bar { B } \, | \, \bar { A } \bar { B } \end {matrix} \right ] , \\ \text { where } \, \bar { A } \bar { B } & = \left ( \begin {matrix} 0 & - 6 \\ 1 & - 5 \end {matrix} \right ) \left ( \begin {matrix} - z \\ 1 \end {matrix} \right ) \\ & = \left ( \begin {matrix} - 6 \\ - z - 5 \end {matrix} \right ) \\ \implies \, { \cal C } ( \bar { A } ,\bar { B } ) & = \left ( \begin {matrix} - z & - 6 \\ 1 & - z - 5 \end {matrix} \right ) . \\ \det { \cal C } & = z ( z + 5 ) + 6 \\ & = z ^ 2 + 5 z + 6 \\ & = 0 \text { for $ z = - 2 $ or $ z = - 3 $ .} \end {align*} C ( A ˉ , B ˉ ) where A ˉ B ˉ ⟹ C ( A ˉ , B ˉ ) det C = [ B ˉ ∣ A ˉ B ˉ ] , = ( 0 1 − 6 − 5 ) ( − z 1 ) = ( − 6 − z − 5 ) = ( − z 1 − 6 − z − 5 ) . = z ( z + 5 ) + 6 = z 2 + 5 z + 6 = 0 for z = − 2 or z = − 3 .
بنابراین، تحقق فرم کانونی مشاهده پذیر تابع تبدیل G ( s ) = s − z s 2 + 5 s + 6 G ( s ) = \dfrac { s - z } { s ^ 2 + 5 s + 6 } G ( s ) = s 2 + 5 s + 6 s − z z = − 2 z = -2 z = − 2 z = − 3 z = -3 z = − 3
حذف صفر-قطب
میخواهیم ببینیم وقتی z = − 2 z = -2 z = − 2 G ( s ) G(s) G ( s )
$$ \large \begin {align*} \require {cancel}<br />
G ( s ) & = \left . \frac { s - z } { s ^ 2 + 5 s + 6 } \right | _ { z = - 2 } \\<br />
& = \frac { \cancel { s + 2 } } { ( \cancel { s + 2 } ) ( s + 3 ) } \\<br />
& = \frac { 1 } { s + 3 } .<br />
\end {align*} $$
همانگونه که میبینیم، حذف صفر-قطب رخ داده است. وقتی z = − 2 z =-2 z = − 2 G ( s ) G(s) G ( s )
x ˙ 1 = − 3 x 1 + u , y = x 1 ⟹ G ( s ) = 1 s + 3 . \large \dot { x } _ 1 = - 3 x _ 1 + u , \, y = x _ 1 \quad \implies \quad G ( s ) = \frac { 1 } { s + 3 } . x ˙ 1 = − 3 x 1 + u , y = x 1 ⟹ G ( s ) = s + 3 1 .
از طرف دیگر، اگر از دیدگاه دیگری به تابع تبدیل نگاه کنیم، میتوانیم تحقق آن را با یک مدل فضای حالت کنترل پذیر یکبعدی بنویسیم:
x ˙ 1 = − 3 x 1 + u , y = x 1 \large \dot { x } _ 1 = - 3 x _ 1 + u , \, y = x _ 1 x ˙ 1 = − 3 x 1 + u , y = x 1
یا اینکه آن را به صورت مدل فضای حالت دو بعدی کنترل ناپذیر زیر نمایش دهیم:
( x ˙ 1 x ˙ 2 ) = ( 0 − 6 1 − 5 ) ( x 1 x 2 ) + ( 2 1 ) u , y = ( 1 0 ) ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \left ( \begin {matrix} 0 & - 6 \\ 1 & - { 5 } \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \left ( \begin {matrix} 2 \\ 1 \end {matrix} \right ) u , \\ y & = \left ( \begin {matrix} 1 & 0 \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = ( 0 1 − 6 − 5 ) ( x 1 x 2 ) + ( 2 1 ) u , = ( 1 0 ) ( x 1 x 2 ) .
واضح است که مدل فضای حالت اخیر، بهترین تحقق یک تابع تبدیل مرتبه اول با بیش از یک متغیر حالت نیست (به دلیل آنکه تحقق مینیمال نیست).
بنابراین، میتوان گفت که بُعد حالت تحقق یک تابع تبدیل نیز منحصر به فرد نیست.
از میان همه تحققهای غیرمینیمال یک تابع تبدیل، یک مورد وجود دارد که از همه بدتر است. تحقق تابع G ( s ) = 1 s + 3 G(s) = \frac{1}{s+3} G ( s ) = s + 3 1
x ˙ 1 = − 3 x 1 + u x ˙ 2 = 100 x 2 y = x 1 . ( 6 ) \large \begin {align*} \dot { x } _ 1 & = - 3 x _ 1 + u \\ \dot { x } _ 2 & = 1 0 0 x _ 2 \\ y & = x _ 1 . \end{align*} \; \; \; \; \; (6) x ˙ 1 x ˙ 2 y = − 3 x 1 + u = 100 x 2 = x 1 . ( 6 )
همانطور که میدانیم، یک متغیر حالت x 1 x _ 1 x 1 G ( s ) = 1 s + 3 G ( s ) = \frac { 1 } { s + 3 } G ( s ) = s + 3 1 x 2 x _ 2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 1 x _1 x 1 u u u
توجه به سه نکته زیر ضروری است:
در تحقق مینیمال بالا، x 2 x_2 x 2 u u u x 2 x_2 x 2
متغیر حالت x 2 x _ 2 x 2
دینامیک x 2 x _2 x 2 x 2 ( t ) ∝ e 100 t x_2(t) \propto e^{100 t} x 2 ( t ) ∝ e 100 t
یک تابع تبدیل (مرتبه پایینتر) میتواند از رفتار متغیر حالت درونی نامطلوب (مدل فضای حالت با بعد بالاتر) جلوگیری کند.
حذف صفر-قطب و پایداری
در حذف قطب-صفر، تابع تبدیل اطلاعات کمتری نسبت به مدل فضای حالت در اختیار ما قرار میدهد؛ زیرا برخی دینامیکها پنهان هستند.
این دینامیکها میتوانند خوب (پایدار) یا بد (ناپایدار) باشند، اما نتوان آنها را از تابع تبدیل تشخیص داد.
بنابراین، طبق تعریف اصلی پایداری، نباید قطبی در سمت محور موهومی در صفحه مختلط وجود داشته باشد. در حذف قطب-صفر ممکن است قطبی (مقدار ویژهای از ماتریس A A A
بنابراین، مفهومی به نام پایداری داخلی (Internal Stability) را در فضای حالت تعریف میکنیم. مدل فضای حالتی با ماتریسهای (A , B , C , D A, B , C , D A , B , C , D A A A
معادله (۱) را به فرم ماتریسی زیر بازنویسی میکنیم:
( x ˙ 1 x ˙ 2 ) = ( − 3 0 0 100 ) ( x 1 x 2 ) + ( 1 0 ) u , y = ( 1 0 ) ( x 1 x 2 ) . \large \begin {align*} \left ( \begin {matrix} \dot { x } _ 1 \\ \dot { x } _ 2 \end {matrix} \right ) & = \left ( \begin {matrix} - 3 & 0 \\ 0 & 1 0 0 \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) + \left ( \begin {matrix} 1 \\ 0 \end {matrix} \right ) u , \\ y & = \left ( \begin {matrix} 1 & 0 \end {matrix} \right ) \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) . \end {align*} ( x ˙ 1 x ˙ 2 ) y = ( − 3 0 0 100 ) ( x 1 x 2 ) + ( 1 0 ) u , = ( 1 0 ) ( x 1 x 2 ) .
تابع تبدیل متناظر با مدل فضای حالت بالا به صورت زیر محاسبه میشود:
$$ \large \begin {align*} \require {cancel}<br />
G ( s ) & = C ( s I - A ) ^ { - 1 } B \\<br />
& = \left ( \begin {matrix} 1 & 0 \end {matrix} \right ) \left ( s I -\left ( \begin {matrix} - 3 & 0 \\ 0 & 1 0 0 \end {matrix} \right ) \right ) ^ { - 1 }<br />
\left ( \begin {matrix} 1 \\ 0 \end {matrix} \right ) \\<br />
& = \frac { \cancel { s - 1 0 0 } } { ( s + 3 ) ( \cancel { s - 1 0 0 } ) } \\<br />
& = \frac { 1 } { s + 3 } .<br />
\end {align*} $$
همانگونه که میبینیم، مد ناپایدار که متناظر با قطب ناپایدار حلقه باز s = 100 s = 100 s = 100 G ( s ) = 1 s + 3 G ( s ) = \frac { 1 } { s + 3 } G ( s ) = s + 3 1 G ( s ) G(s) G ( s )
بنابراین، میتوان گفت پایداری داخلی، یک شرط قویتر برای پایداری است و معادل نداشتن قطب حلقه باز در سمت راست محور موهومی و عدم حذف قطب-صفر در سمت راست محور موهومی است.
تبدیل مختصات
اکنون که میدانیم یک تابع تبدیل میتواند تحققهای مختلفی در فضای حالت داشته باشد، یک فرایند نظاممند را برای به دست آوردن تحققهایی که مشخصات قابل توجهی مانند کنترل پذیری دارند، معرفی میکنیم.
این روش تبدیل مختصات نام دارد.
شکل ۱: تبدیل مختصات نگاشت زیر را در نظر بگیرید:
τ : x ↦ x ˉ = T x , where T ∈ R n × n is nonsingular ⟺ x = T − 1 x ˉ , \large \begin {align*} \tau : x \mapsto \bar { x } & = T x , \text { where } \, T \in \mathscr { R } ^ { n \times n } \text { is nonsingular } \\ \iff x & = T ^ { - 1 } \bar { x } , \end {align*} τ : x ↦ x ˉ ⟺ x = T x , where T ∈ R n × n is nonsingular = T − 1 x ˉ ,
این نگاشت بدین معنی است که میتوانیم مختصات مختلف را به یکدیگر تبدیل کنیم. برای مثال:
( x 1 x 2 ) ⟼ ( x ˉ 1 x ˉ 2 ) = ( x 1 + x 2 x 1 − x 2 ) . \large \begin {align*} \left ( \begin {matrix} x _ 1 \\ x _ 2 \end {matrix} \right ) \longmapsto \left ( \begin {matrix} \bar { x } _ 1 \\ \bar { x } _ 2 \end {matrix} \right ) = \left ( \begin {matrix} x _ 1 + x _ 2 \\ x _ 1 - x _ 2 \end {matrix} \right ) . \end {align*} ( x 1 x 2 ) ⟼ ( x ˉ 1 x ˉ 2 ) = ( x 1 + x 2 x 1 − x 2 ) .
از آنجایی که det T = − 2 \det T = -2 det T = − 2 T T T
T − 1 = 1 det T ( − 1 − 1 − 1 1 ) = ( 1 2 1 2 1 2 − 1 2 ) \large \begin {align*} T ^ { - 1 } & = \frac { 1 } { \det T } \left ( \begin {matrix} - 1 & - 1 \\ - 1 & 1 \end {matrix} \right ) = \left ( \begin {matrix} \frac { 1 } { 2 } & \frac { 1 } { 2 } \\ \frac { 1 } { 2 } & - \frac { 1 } { 2 } \end {matrix} \right ) \end {align*} T − 1 = det T 1 ( − 1 − 1 − 1 1 ) = ( 2 1 2 1 2 1 − 2 1 )
همچنین میتوانیم مستقیماً x ˉ \bar{x} x ˉ x x x
x ˉ 1 + x ˉ 2 = 2 x 1 , x ˉ 1 − x ˉ 2 = 2 x 2 . \large \begin {align*} \bar { x } _ 1 + \bar { x } _ 2 & = 2 x _ 1 , \\ \bar { x } _ 1 - \bar { x } _ 2 & = 2 x _ 2 . \end {align*} x ˉ 1 + x ˉ 2 x ˉ 1 − x ˉ 2 = 2 x 1 , = 2 x 2 .
تبدیل مختصات و مدلهای فضای حالت
مدل فضای حالت زیر را در نظر بگیرید:
x ˙ = A x + B u , y = C x \large \begin {align*} \dot { x } & = A x + B u , \\ y & = C x \end {align*} x ˙ y = A x + B u , = C x
همچنین تغییر x ˉ = T x \bar{x} = Tx x ˉ = T x T T T
مختصات جدید اینگونه است:
x ˉ ˙ = T x ˙ = T x ˙ = T ( A x + B u ) = T ( A T − 1 x ˉ + B u ) ( x = T − 1 x ˉ ) = T A T − 1 ⏟ A ˉ x ˉ + T B ⏟ B ˉ u , y = C x = C T − 1 ⏟ C ˉ x ˉ . \large \begin {align*} \dot { \bar { x } } & = \dot { T x } &\\ & = T \dot { x } & \\ & = T ( A x + B u ) \\ & = T ( A T ^ { - 1 } \bar { x } + B u ) & \text {($ x = T ^ { - 1 } \bar { x } $)} \\ & = \underbrace { T A T ^ { - 1 } } _ { \bar { A } } \bar { x } + \underbrace { T B } _ { \bar { B } } u , \\ y & = C x \\ & = \underbrace { C T ^ { - 1 } } _ { \bar {C } } \bar { x } . \end {align*} x ˉ ˙ y = T x ˙ = T x ˙ = T ( A x + B u ) = T ( A T − 1 x ˉ + B u ) = A ˉ T A T − 1 x ˉ + B ˉ TB u , = C x = C ˉ C T − 1 x ˉ . ( x = T − 1 x ˉ )
بنابراین، با تبدیل خطی τ : x ↦ T x \tau : x \mapsto Tx τ : x ↦ T x
x ˙ = A x + B u , y = C x , → T x ˉ ˙ = A ˉ x ˉ + B ˉ u , y = C ˉ x ˉ , \large \begin {align*} \begin {array} { l } \dot { x } = A x + B u , \\ y = C x , \end {array} \quad \xrightarrow { \quad T \quad } \quad \begin {array} { l } \dot { \bar { x } } = \bar { A } \bar { x } + \bar { B } u , \\ y = \bar { C } \bar { x } , \end {array} \end {align*} x ˙ = A x + B u , y = C x , T x ˉ ˙ = A ˉ x ˉ + B ˉ u , y = C ˉ x ˉ ,
که در آن:
A ˉ = T A T − 1 , B ˉ = T B , C ˉ = C T − 1 . \large \begin {align*} \bar { A } = T A T ^ { - 1 } , \, \bar { B } = T B , \, \bar { C } = C T ^ { - 1 } . \end {align*} A ˉ = T A T − 1 , B ˉ = TB , C ˉ = C T − 1 .
اما این پرسش پیش میآید که تابع تبدیل و ماتریس کنترل پذیری چه تغییری میکنند؟
قضیه: تابع تبدیل، با اعمال یک تبدیل خطی تغییری نمیکند.
اثبات: کافی است تابع تبدیل را با استفاده از فرمول مربوطه به دست آوریم:
G ˉ ( s ) = C ˉ ( s I − A ˉ ) − 1 B ˉ = ( C T − 1 ) ( s I − T A T − 1 ) − 1 ( T B ) = C T − 1 ( s T I T − 1 − T A T − 1 ) − 1 T B = C T − 1 [ T ( s I − A ) T − 1 ] − 1 T B = C T − 1 T ⏟ I ( s I − A ) − 1 T − 1 T ⏟ I B = C ( s I − A ) − 1 B = G ( s ) . \large \begin {align*} \bar { G } ( s ) & = \bar { C } ( s I - \bar { A } ) ^ { - 1 } \bar { B } \\ & = ( C T ^ { - 1 } ) \left ( s I - T A T ^ { - 1 } \right ) ^ { - 1 } ( T B ) \\ & = C T ^ { - 1 } \left ( s T I T ^ { - 1 } - T A T ^ { - 1 } \right ) ^ { - 1 } T B \\ & = C T ^ { - 1 } \left [ T \left ( s I - A \right ) T ^ { - 1 } \right ] ^ { - 1 } T B \\ & = C \underbrace { T ^ { - 1 } T } _ { I } \left ( s I - A \right ) ^ { - 1 } \underbrace { T ^ { - 1 } T } _ { I } B \\ & = C \left ( s I - A \right ) ^ { - 1 } B \\ & = G ( s ) . \end {align*} G ˉ ( s ) = C ˉ ( s I − A ˉ ) − 1 B ˉ = ( C T − 1 ) ( s I − T A T − 1 ) − 1 ( TB ) = C T − 1 ( s T I T − 1 − T A T − 1 ) − 1 TB = C T − 1 [ T ( s I − A ) T − 1 ] − 1 TB = C I T − 1 T ( s I − A ) − 1 I T − 1 T B = C ( s I − A ) − 1 B = G ( s ) .
با توجه به اینکه تابع تبدیل، با تبدیل خطی تغییر نمیکند، میتوانیم بگوییم:
قطبهای حلقه باز تغییر نمیکنند؛
چندجملهای مشخصه تغییر نمیکند. صحت این گفته را میتوان به سادگی تحقیق کرد:
det ( s I − A ˉ ) = det ( s I − T A T − 1 ) = det [ T ( s I − A ) T − 1 ] = det T ⋅ det ( s I − A ) ⋅ det T − 1 = det ( s I − A ) . \large \begin {align*} \det ( s I - \bar { A } ) & = \det ( s I - T A T ^ { - 1 } ) \\ & = \det \left [ T ( s I - A ) T ^ { - 1 } \right ] \\ & = \det T \cdot \det ( s I - A ) \cdot \det T ^ { - 1 } \\ & = \det ( s I - A ) . \end {align*} det ( s I − A ˉ ) = det ( s I − T A T − 1 ) = det [ T ( s I − A ) T − 1 ] = det T ⋅ det ( s I − A ) ⋅ det T − 1 = det ( s I − A ) .
قضیه: کنترل پذریری تحت شرایط تبدیل خطی تغییر نمیکند.
اثبات: این گفته را با استقرا اثبات میکنیم. فرض کنید حکم گفته شده، برای هر k = 0 , 1 , … k = 0,1,\ldots k = 0 , 1 , …
A ˉ k B ˉ = ( T A T − 1 ) k T B = T A k T − 1 T B = T A k B . \large \begin {align*} \bar { A } ^ k \bar { B } & = ( T A T ^ { - 1 } ) ^ k T B \\ & = T A ^ { k } T ^ { -1 } T B \\ & = T A ^ k B . \end {align*} A ˉ k B ˉ = ( T A T − 1 ) k TB = T A k T − 1 TB = T A k B .
بنابراین، ماتریس کنترل پذیری به صورت زیر خواهد بود:
C ( A ˉ , B ˉ ) = [ T B ∣ T A B ∣ … ∣ T A n − 1 B ] = T [ B ∣ A B ∣ … ∣ A n − 1 B ] = T C ( A , B ) . \large \begin {align*} { \cal C } ( \bar { A } , \bar { B } ) & = [ \, T B \, | \, T A B \, | \, \ldots \, | \, T A ^ { n - 1 } B \, ] \\ & = T [ \, B \, | \, A B \, | \, \ldots \, | \, A ^ { n - 1 } B \, ] \\ & = T { \cal C }( A , B ) . \end {align*} C ( A ˉ , B ˉ ) = [ TB ∣ T A B ∣ … ∣ T A n − 1 B ] = T [ B ∣ A B ∣ … ∣ A n − 1 B ] = T C ( A , B ) .
همانطور که میبینیم، det T ≠ 0 \det T \neq 0 det T = 0 det C ( A ˉ , B ˉ ) ≠ 0 \det {\cal C}(\bar{A},\bar{B}) \neq 0 det C ( A ˉ , B ˉ ) = 0 det C ( A , B ) ≠ 0 \det {\cal C}(A,B) \neq 0 det C ( A , B ) = 0
بنابراین، سیستم جدید کاملاً کنترل پذیر است، اگر و فقط اگر سیستم اصلی کنترل پذیر باشد.
ماتریس کنترل پذیری ممکن است تغییر کند:
C ( A ˉ , B ˉ ) ⏟ new = T ⏟ coord. trans. C ( A , B ) ⏟ old ⇕ T = C ( A ˉ , B ˉ ) [ C ( A , B ) ] − 1 . \large \begin{align*} \underbrace{{\cal C}(\bar{A},\bar{B})}_{\text{new}} &= \underbrace{T}_{\text{coord.} \atop \text{trans.}} \underbrace{{\cal C}(A,B)}_{\text{old}} \\ & \Updownarrow \\ T &= {\cal C}(\bar{A},\bar{B}) \left[\, {\cal C}(A,B)\, \right]^{-1}. \end{align*} new C ( A ˉ , B ˉ ) T = trans. coord. T old C ( A , B ) ⇕ = C ( A ˉ , B ˉ ) [ C ( A , B ) ] − 1 .
این، یک راهکار برای به دست آوردن تحقق یک تابع تبدیل از یک تحقق دیگر است.
مثال ۳
سیستمی را با ماتریسهای حالت و ورودی زیر در نظر بگیرید:
A = ( − 15 8 − 15 7 ) , B = ( 1 1 ) \large A = \left( \begin {matrix} - 1 5 & 8 \\ - 1 5 & 7 \end {matrix} \right ) , \,\, B = \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) A = ( − 15 − 15 8 7 ) , B = ( 1 1 )
یک تبدیل خطی پیدا کنید که در صورت امکان، این مدل فضای حالت را به فرم کانونی کنترل پذیر تبدیل کند.
حل: در گام اول، کنترل پذیری را بررسی میکنیم:
A B = ( − 15 8 − 15 7 ) ( 1 1 ) = ( − 7 − 8 ) ⟹ C = ( 1 − 7 1 − 8 ) . \large \begin {align*} A B & = \left ( \begin {matrix} - 1 5 & 8 \\ - 1 5 & 7 \end {matrix} \right ) \left ( \begin {matrix} 1 \\ 1 \end {matrix} \right ) = \left ( \begin {matrix} - 7 \\ - 8 \end {matrix} \right ) \\ \implies { \cal C } & = \left ( \begin {matrix} 1 & - 7 \\ 1 & - 8 \end {matrix} \right ) . \end {align*} A B ⟹ C = ( − 15 − 15 8 7 ) ( 1 1 ) = ( − 7 − 8 ) = ( 1 1 − 7 − 8 ) .
از آنجایی که det C = − 1 \det {\cal C} = -1 det C = − 1
در گام دوم باید ماتریس کنترل پذیری مطلوب C ( A ˉ , B ˉ ) {\cal C}(\bar{A},\bar{B}) C ( A ˉ , B ˉ ) A ˉ \bar{A} A ˉ B ˉ \bar{B} B ˉ
A ˉ = ( 0 1 − a 2 − a 1 ) , B ˉ = ( 0 1 ) , \large \begin {align*} \bar { A } & = \left ( \begin {matrix} 0 & 1 \\ - a _ 2 & - a _ 1 \end {matrix} \right ) , \\ \bar { B } & = \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) , \end {align*} A ˉ B ˉ = ( 0 − a 2 1 − a 1 ) , = ( 0 1 ) ,
بنابراین، باید ضرایب نامعلوم a 1 a_1 a 1 a 2 a_2 a 2
پیشتر گفتیم که چندجملهای مشخصه تحت شرایط تبدیل خطی بدون تغییر میماند. بنابراین:
det ( I s − A ) = det ( I s − A ˉ ) ⟹ det ( s + 15 − 8 15 s − 7 ) = det ( s − 1 a 2 s + a 1 ) ⟹ ( s + 15 ) ( s − 7 ) + 120 = s ( s + a 1 ) + a 2 s 2 + 8 s + 15 = s 2 + a 1 s + a 2 . \large \begin {align*} \det ( I s - A ) & = \det ( I s - \bar { A } ) \\ \implies \det \left ( \begin {matrix} s + 1 5 & - 8 \\ 1 5 & s - 7 \end {matrix} \right ) & = \det \left ( \begin {matrix} s & - 1 \\ a _ 2 & s + a _ 1 \end {matrix} \right ) \\ \implies ( s + 1 5 ) ( s - 7 ) + 1 2 0 & = s ( s + a _ 1 ) + a _ 2 \\ s ^ 2 + \color {red} { 8 } s + \color {blue} { 1 5 } & = s ^ 2 + \color {red} { a _ 1 } s + \color {blue} { a _ 2 } . \end {align*} det ( I s − A ) ⟹ det ( s + 15 15 − 8 s − 7 ) ⟹ ( s + 15 ) ( s − 7 ) + 120 s 2 + 8 s + 15 = det ( I s − A ˉ ) = det ( s a 2 − 1 s + a 1 ) = s ( s + a 1 ) + a 2 = s 2 + a 1 s + a 2 .
با مشاهده و تطبیق ضرایب دو طرف معادله، نتیجه به صورت زیر خواهد بود:
A ˉ = ( 0 1 − 15 − 8 ) , B ˉ = ( 0 1 ) \large \begin {align*} \bar { A } = \left ( \begin {matrix} 0 & 1 \\ - 1 5 & - 8 \end {matrix} \right ) , \, \bar { B } & = \left ( \begin {matrix} 0 \\ 1 \end {matrix} \right ) \end {align*} A ˉ = ( 0 − 15 1 − 8 ) , B ˉ = ( 0 1 )
بنابراین، ماتریس کنترل پذیری به صورت زیر در میآید:
C ( A ˉ , B ˉ ) = [ B ˉ ∣ A ˉ B ˉ ] = ( 0 1 1 − 8 ) . \large \begin {align*} { \cal C } ( \bar { A } , \bar { B } ) = [ \, \bar { B } \, | \, \bar { A } \bar { B } \, ] = \left ( \begin {matrix} 0 & 1 \\ 1 & - 8 \end {matrix} \right ) . \end {align*} C ( A ˉ , B ˉ ) = [ B ˉ ∣ A ˉ B ˉ ] = ( 0 1 1 − 8 ) .
در مرحله سوم، باید T T T
T = C ( A ˉ , B ˉ ) ⋅ [ C ( A , B ) ] − 1 \large T = { \cal C } ( \bar { A } ,\bar { B } ) \cdot \left [ \, { \cal C } ( A , B ) \, \right ] ^ { - 1 } T = C ( A ˉ , B ˉ ) ⋅ [ C ( A , B ) ] − 1
بنابراین:
C ( A , B ) = ( 1 − 7 1 − 8 ) , [ C ( A , B ) ] − 1 = ( 1 − 7 1 − 8 ) − 1 = 1 − 1 ( − 8 7 − 1 1 ) = ( 8 − 7 1 − 1 ) , C ( A ˉ , B ˉ ) = ( 0 1 1 − 8 ) . ⟹ T = ( 0 1 1 − 8 ) ( 8 − 7 1 − 1 ) = ( 1 − 1 0 1 ) . \large \begin {align*} { \cal C } ( A , B ) & = \left ( \begin {matrix} 1 & - 7 \\ 1 & - 8 \end {matrix} \right ) , \\ \left [ \, { \cal C } ( A , B ) \, \right ] ^ { - 1 } & = \left ( \begin {matrix} 1 & - 7 \\ 1 & - 8 \end {matrix} \right ) ^ { - 1 } \\ & = \frac { 1 } { - 1 } \left ( \begin {matrix} - 8 & 7 \\ - 1 & 1 \end {matrix} \right ) \\ & = \left ( \begin {matrix} 8 & - 7 \\ 1 & - 1 \end {matrix} \right ) , \\ { \cal C } ( \bar { A } , \bar { B } ) & = \left ( \begin {matrix} 0 & 1\\ 1 & - 8 \end {matrix} \right ) . \\ \implies T & = \left ( \begin {matrix} 0 & 1 \\ 1 & - 8 \end {matrix} \right ) \left ( \begin {matrix} 8 & - 7 \\ 1 & - 1 \end {matrix} \right ) \\ & = \left ( \begin {matrix} 1 & - 1 \\ 0 & 1 \end {matrix} \right ) . \end {align*} C ( A , B ) [ C ( A , B ) ] − 1 C ( A ˉ , B ˉ ) ⟹ T = ( 1 1 − 7 − 8 ) , = ( 1 1 − 7 − 8 ) − 1 = − 1 1 ( − 8 − 1 7 1 ) = ( 8 1 − 7 − 1 ) , = ( 0 1 1 − 8 ) . = ( 0 1 1 − 8 ) ( 8 1 − 7 − 1 ) = ( 1 0 − 1 1 ) .
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^