بوت استرپ در علم داده به زبان پایتون | راهنمای کاربردی

یکی از تکنیک‌های مهم و ناپارامتری برای برآورد خطای مدل‌ها و برآوردگرهای آماری، استفاده از نمونه‌گیری مجدد (بازنمونه‌گیری- Resampling) و محاسبه برآوردگر تحت نمونه‌های مختلف است. در این صورت واریانس یا انحراف معیار مقدار برآوردگرها حاصل از نمونه‌های مختلف، به عنوان خطای برآوردگر در نظر گرفته می‌شود. در حقیقت، چنین شیوه‌ای برای پیدا کردن خطای برآوردگر را «بوت استرپ» (Bootstrap) می‌نامند. از آنجایی که بوت استرپ در علم داده یک روش و تکنیک رایانه‌ای است، در این نوشتار به کمک زبان برنامه‌نویسی پایتون به پیاده سازی آن پرداخته‌ایم.

البته توجه داشته باشید که اصطلاح بوت استرپ مربوط به بند یا تسمه‌ای است که روی کفش دوخته شده و توسط آن چکمه یا کفش‌های سنگین را به پا می‌کنند، آمارشناسانی به نام «بردلی افرون» (Bradley Efron) این روش ابداعی خود را بوت استرپ نام نهاد تا نشان دهد که عمل محاسبه خطای برآوردگر که بدون دانستن توزیع آن، به سختی صورت می‌گیرد، توسط روش او به سادگی ولی به صورت تکرار یک کار ثابت، قابل اجرا است و خوشبختانه از تقریب خوبی هم برخوردار است.

به منظور آشنایی بیشتر با شیوه بازنمونه‌گیری و تکنیک‌های تحلیل براساس آن، نوشتار جک نایف و بوت استرپ (Jackknife and Bootstrap) روش های بازنمونه‌ گیری — به زبان ساده را مطالعه کنید. همچنین خواندن نمونه‌گیری و بازنمونه‌گیری آماری (Sampling and Re-sampling) — به زبان ساده نیز خالی از لطف نیست.

بوت استرپ در علم داده به زبان پایتون

بوت استرپ در علم داده روشی قدرتمند و مبتنی بر رایانه برای استنباط آماری بدون تکیه بر فرضیه‌های زیاد است. این فقط جادویی است که از یک نمونه داده می‌توان یک توزیع نمونه برداری تولید کرد. برای استنباط آماری در بوت استرپ هیچ احتیاجی به اطلاع از توزیع آماری برآوردگرها نیست. به این ترتیب «بوت استرپ» (Bootstrap) برای ایجاد «فاصله اطمینان» (Confidence Interval)، «مدل رگرسیونی» (Regression Model)، حتی در زمینه «یادگیری ماشین» (Machine Learning) به طور گسترده‌ای به کار برده می‌شود.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

در این متن ما در مورد دو موضوع وابسته به بوت استرپ در علم داده صحبت خواهیم کرد:

1. ساخت فاصله اطمینان
2. انجام آزمون فرض آماری

البته هر یک از این موارد را هم به کمک روش‌های صریح آماری و هم به کمک بوت استرپ انجام داده و نتایج حاصل را با هم مقایسه می‌کنیم. در این بین با توجه به گستردگی زبان پایتون در انجام روش‌های مطرح در علم داده، کدهایی نیز به این زبان برای اجرای محاسبات و عملیات مربوطه معرفی می‌کنیم.

ساخت فاصله اطمینان با بوت استرپ در علم داده

در دنیای واقعی، به طور صریح در مورد جمعیت یا جامعه آماری و خصوصیات و ویژگی‌های متغیرهای آن اطلاعاتی نداریم. برای مثال جامعه آماری مورد بحث ما آن می‌تواند کل جمعیت کره زمین یا معاملات گذشته در بازار سهام و حتی، گردش مالی حال و آینده یک شرکت باشد. مشکل اصلی این است که با توجه به زیاد بودن اندازه جامعه آماری، مجبور به نمونه‌گیری هستیم تا برآورد مناسبی برای ویژگی‌های آماری جامعه در اختیار داشته باشیم.

در حقیقت برای استنباط و شناخت در مورد پارامتر مربوط به این جمعیت، به توزیع نمونه اعتماد می‌کنیم. نام‌های مختلفی برای آزمون فرضیه و نحوه ایجاد فواصل اطمینان وجود دارد:

• آزمون تی تک نمونه‌ای (T-Test) 
• آزمون t دو نمونه (Two sample t-test) 
• آزمون Z-test) Z)
• آزمون مجذور کای (Chi-squared Test)

یک جایگزین ناپارامتری برای هر یک از این‌ها می‌تواند استفاده از روش Bootstrapping باشد. ما در این نوشتار مثالی را مرور خواهیم کرد تا ببینیم چگونه از توزیع نمونه برای ایجاد فاصله اطمینان برای پارامتر مورد علاقه خود استفاده می‌شود.

هدف: می‌خواهیم ایده‌ای در مورد متوسط ​​قد افرادی كه قهوه می‌نوشند بوسیله نمونه‌های گرفته شده، بدست آوریم.

روش اول: استفاده از شیوه Bootstrapping

فرض بر این است که ما یک مجموعه داده از همه نوشندگان قهوه داریم که در فایلی به نام (coffee_full.csv) ثبت شده است. این فایل را به قالب فشرده از اینجا دریافت کنید. پس از آنکه این فایل را از حالت فشرده خارج کردید، توسط کد زیر می‌توانید آن را فراخوانی کنید.

1coffee_full = pd.read_csv(‘coffee_full.csv’)

نکته: قالب فایل‌های csv. یا (Comma Separated Values) مربوط به پرونده‌های اطلاعاتی است که ستون‌های متغیرها در آن‌ها با علامت کاما (,) از یکدیگر جدا شده‌اند.

فیلم آموزش تجزیه و تحلیل و آماده سازی داده ها با پایتون Python در فرادرس

کلیک کنید

به کمک دستور زیر، یک زیرمجموعه داده به صورت نمونه‌ای ۲۰۰ تایی از پایگاه داده coffee_full ایجاد می‌کنیم. این مجموعه داده را به نام coffee_red نام‌گذاری کرده‌ایم. از این به بعد از این نمونه برای انجام محاسبات استفاده خواهیم کرد. در حقیقت به این ترتیب یک نمونه از جامعه واقعی ایجاد کرده‌ایم.

1coffee_red = coffee_full.sample(n=200)

دستورات زیر را در نظر بگیرید. به کمک این قطعه کد نسبت افرادی که قهوه می‌نوشند در پایگاه داده ما محاسبه و در خروجی قرار می‌گیرد.

1[coffee_red[‘drinks_coffee’]==True].mean()
2---Output---
30.595

در کد پایین نیز میانگین ارتفاع یا قد افراد برحسب اینچ (Inch) محاسبه شده است.

1coffee_red[coffee_red[‘drinks_coffee’]==True]['height'].mean()
2---Output---
368.119 inches

حالا براساس کد زیر، از تکنیک بوت استرپ در علم داده استفاده کرده و یک فاصله اطمینان برای میانگین می‌سازیم.

1# Let's first create an empty list for storing means of bootstrapped samples
2boot_means = []
3# Let's write a loop for creating 1000 bootstrapped samples
4for i in range(1000):
5    bootsample = coffee_red.sample(200, replace=True)
6    bootsample_mean = bootsample.[bootsample[‘drinks_coffee’]==True]['height'].mean()
7    boot_means.append(bootsample_mean)
8boot_means = np.array(boot_means)

برای اطمینان 95٪ یا در حقیقت ۵٪ خطا، براساس ۱0۰ بار نمونه‌گیری، میانگین را برآورد می‌کنیم. از بین آن‌ها، ۲٫۵ درصد از آن‌هایی که کمترین مقدار را دارند حذف خواهیم کرد. همچنین در بین آن‌هایی که بزرگترین مقادیر را دارند نیز ۲٫۵ درصد حذف خواهند شد. باقی میانگین‌‌ها، تشکیل یک فاصله اطمینان ۹۵٪ می‌دهند. در حقیقت کران پایین تا کران بالای این میانگین‌ها، همان فاصله اطمینان ۹۵٪ برای میانگین جامعه آماری است.

1# we build 95% in the middle portion
2np.percentile(boot_means, 2.5), np.percentile(boot_means, 97.5)
3---Output---
4(66.00, 67.59)

فاصله اطمینانی که در کد بالا تولید شده را می‌توان کران‌های میانگین برای قد افراد جامعه با اطمینان ۹۵٪ در نظر گرفت. دستور percentile، صدک‌ها را مشخص می‌کند به همین علت صدک ۲٫۵ و 97٫5 را مشخص کرده‌ایم.

برای نمایش این فاصله اطمینان از یک نمودار فراوانی (Histogram) استفاده می‌کنیم. کدی که در زیر مشاهده می‌کنید به منظور نمایش فراوانی میانگین‌های تولید شده توسط بوت استرپ است. فضا یا ناحیه‌ای که مساحتی برابر با ۹۵٪ کل نمودار را به صورت متقارن از مرکز دارد، همان فاصله اطمینان خواهد بود.

1plt.hist(boot_means, alpha=0.7);
2plt.axvline(np.percentile(boot_means, 2.5), color='red', linewidth=2) ;
3plt.axvline(np.percentile(boot_means, 97.5), color='red', linewidth=2) ;

در تصویر زیر نمودار فراوانی حاصل را مشاهده می‌کنید.

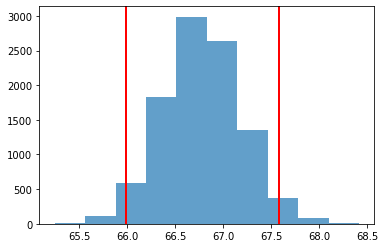
تفسیر فاصله اطمینان

فاصله اطمینان، تعیین کران‌هایی تصادفی است که به واسطه آن با سطح اطمینان مشخصی، می‌توانیم پوششی برای میانگین جامعه ایجاد کنیم. به این ترتیب مثلا می‌گوییم با اطمینان ۹۵٪ مطمئن هستیم که بازه $$(66.0 , 67.59)$$ شامل میانگین جامعه (یعنی میانگین قد افرادی که قهوه می‌نوشند) است.

در کد زیر، نحوه محاسبه میانگین جامعه آماری (همه افرادی که موضوع مورد بحث ما هستند) مشخص شده است.

1coffee_full[coffee_full[‘drinks_coffee’]==True][‘height’].mean()
2---Output---
366.44 inch

واضح است که بازه ارائه شده یعنی $$(66.0 , 67.59)$$ شامل مقدار $$66.44$$ است.

روش دوم: ایجاد فاصله اطمینان به کمک آزمون فرض آماری (t-Test)

روش‌های دیگری نیز برای محاسبه فاصله اطمینان آماری برای پارامتر جامعه وجود دارد. این کار بخصوص هنگام استفاده از توابعی که آزمون مربوط به میانگین را انجام می‌دهند قابل اجرا است.

کدی که با پایتون برای انجام آزمون مقایسه میانگین نوشته شده در ادامه قابل مشاهده است. در قسمت عبارت cm.tconfint_diff برای اختلاف میانگین قد دو گروهی که در نمونه (coffee_red) و غیر از آن هستند، یک فاصله اطمینان تشکیل شده است.

1import statsmodels.stats.api as sm
2X1 = coffee_red[coffee_red['drinks_coffee']==True]['height'] 
3X2 = coffee_red[coffee_red['drinks_coffee']==False]['height']
4cm = sm.CompareMeans(sm.DescrStatsW(X1), sm.DescrStatsW(X2))
5print (cm.tconfint_diff(usevar='unequal'))

با اجرای این کد مشاهده می‌کنید که اختلاف ناچیزی بین نتیجه فاصله اطمینان بوسیله بوت استرپ و روش مستقیم آماری وجود دارد که البته ناشی از ناپارامتری بودن روش بوت استرپ است. واضح است که روش مستقیم به شرطی که توزیع داده‌ها معلوم باشد، دقیق‌تر و قابل اعتمادتر است.

به نظر می‌رسد که باید اندازه فاصله اطمینان (تفاضل کران بالا و پایین) در روش مستقیم کوچکتر از روش بوت استرپ باشد.

آزمون فرض آماری و بوت استرپ در علم داده

به عنوان یک تحلیل‌گر داده، باید با مفهوم آزمون فرض و فرضیه آماری آشنا باشید. در صورتی که با این اصطلاحات آشنایی ندارید بهتر است مطالب تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات را مطالعه کنید.

فیلم آموزش آزمون آماری و پی مقدار p-value در فرادرس

کلیک کنید

آزمون فرض آماری، تکنیکی است که به کمک آن نسبت به پارامتر مورد نظر جامعه، دو فرضیه را به کار گرفته و طبق نتایج حاصل از نمونه‌گیری، نسبت به رد یا تایید یکی از آن‌ها اقدام می‌کنیم.

با توجه به آزمون فرض آماری، در مورد میانگین قد افراد می‌خواهیم فرضیه سازی کرده و طبق نمونه‌ای که گرفته‌ایم، فرضیه‌ها را مورد تایید یا رد قرار دهیم. توجه داشته باشید که می‌خواهیم بدانیم آیا متوسط قد افرادی که قهوه میل می‌کنند، بلندتر از ۷۰ اینچ است؟

همانطور که می‌دانید آزمون فرض آماری از دو فرضیه به نام‌های فرض صفر و فرض مقابل تشکیل شده است. برای مسئله ما، این فرضیه‌ها را به صورت زیر در نظر گرفته‌ایم. توجه داشته باشید که معمولا نظر یا حکمی که از قبل وجود داشته در «فرض صفر» یا «فرض نال» (Null Hypothesis) نوشته شده و حکم مورد نظر برای محقق (که معمولا در خلاف جهت حکم قبلی است) به عنوان «فرض مقابل» یا «فرض جایگزین» (Alternative Hypothesis) نوشته می‌شود.

$$\large \begin{cases} H_0 : & \mu_{cof} \leq 70 \\ H_A: & \mu_{cof} > 70 \end{cases}$$

حال به منظور تصمیم نسبت به صحت هر یک از این فرضیه‌ها، از دو روش کمک می‌گیریم. در ابتدا با تکیه بر تکنیک بوت استرپ در علم داده فرضیه‌ها را مورد آزمون قرار می‌دهیم. سپس با تکنیک‌های شبیه‌سازی، صحت فرض صفر را می‌سنجیم.

روش اول: بررسی امکان‌پذیر بودن فرض صفر به کمک بوت استرپ

در این بخش با ۱۰۰۰ بار شبیه‌سازی داده‌ها و محاسبه میانگین نمونه‌ای، یک توزیع نمونه‌ای و فاصله اطمینان برای میانگین جامعه می‌سازیم. می‌دانیم که اگر فاصله اطمینان تولید شده، مطابق با فرض صفر باشد، آن فرض تایید خواهد شد. همچنین اگر فاصله اطمینان با فرض مقابل مطابقت داشته باشد، فرض صفر را رد کرده و فرض مقابل را تایید می‌کنیم.

1means = []
2for i in range(10000):
3   bootsample = sample_df.sample(n=150, replace = True)
4   bootsample_mean = bootsample[bootsample['drinks_coffee']==True]
5   means.append(bootsample_mean['height'].mean())
6means = np.array(means)
7np.percentile(means, 2.5), np.percentile(means, 97.5)
8---Output---
9(66.00, 67.59

همانطور که مشخص است فاصله اطمینان ۹۵٪ تولید شده با کران‌های ۶۶٫۰ و ۶۷٫۵۹ بدست آمده است. مقدار ۷۰ که در فرض مقابل به آن اشاره شده، در این باز قرار نمی‌گیرد و بازه کوچکتر از ۷۰ است. پس می‌توان گفت دلیلی بر رد فرض صفر وجود ندارد و فرض مقابل رد می‌شود.

روش دوم: شبیه‌سازی فرضیه صفر

فرض کنید که فرضیه صفر در آزمون فرض آماری صحیح باشد. به این ترتیب اگر از توزیع نرمال با توجه به این فرض، شبیه سازی کرده و مقادیر زیادی تولید کنیم، انتظار داریم که میانگین نمونه‌ای نیز به آن‌ها نزدیک باشد و فرض صفر تایید شود.

در دستور زیر، به شبیه‌سازی از توزیع نرمال با میانگین ۷۰ و انحراف معیار میانگین‌ها پرداخته‌ایم. به یاد داشته باشید که ۷۰ مقدار مربوط به کران‌های فرض صفر یا فرض مقابل است.

1null_vals = np.random.normal(loc = 70, scale = np.std(means), size =10000)

هر بار نمونه‌گیری یک میانگین تولید کرده که براساس فرض صفر ساخته شده است. به کمک این شبیه‌سازی می‌توان به این پرسش پاسخ داد که میانگین نمونه‌ای در توزیع نرمال مربوطه، کجا قرار می‌گیرد؟

1plt.hist(null_vals, alpha=0.7);
2plt.axvline(sample_mean, color = 'red', linewidth=2);

خروجی این کد، در نموداری که در تصویر زیر می‌بینید، ظاهر شده است.

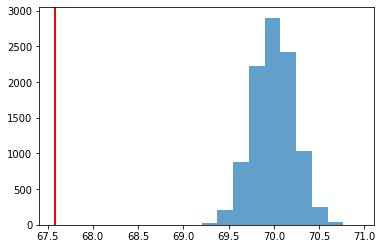
با توجه به فرضیه‌های آماری گفته شده، باید فرض صفر تایید شده و فرض مقابل رد شود.

1p_value = (null_vals > sample_mean).mean()
2p_value
3--Output--
41.0

مقادیر بزرگ برای p-value، نشانگر تایید فرض صفر هستند و نمی‌توانند دلیلی برای رد فرض صفر باشند. به این ترتیب به نظر می‌رسد که میانگین جامعه (قد کسانی که قهوه می‌نوشند) کمتر یا برابر با ۷۰ اینچ است. در مورد p-value به نکات زیر دقت کنید.

• از لحاظ تصویری، p-value سطح زیر منحنی مربوط به تصویر بالا است که در طرف راست خط قرمز رنگ قرار دارند. از آنجایی که همه مقادیر در سمت راست خط قرمز هستند، همه مقادیر در تایید فرض صفر، سهم دارند و هیچ شاهدی برای رد فرض صفر وجود ندارد.
• در اینجا p-value را به عنوان میانگین (یا مقدار احتمال) تعداد حالت‌هایی در نظر گرفتیم که نمونه‌های استخراج شده یا شبیه‌سازی شده از توزیع نرمال (با میانگین ۷۰ و واریانس برابر با واریانس نمونه) از مقدار میانگین نمونه‌ای (مقدار 67٫5) بیشتر هستند.

به منظور آشنایی بیشتر با نحوه محاسبه مقدار احتمال (p-value) بهتر است نوشتار مقدار احتمال (p-Value) در آزمون فرض آماری — به زبان ساده را نیز مطالعه کنید.

خلاصه و جمع‌بندی

در این نوشتار با توجه به شیوه باز نمونه‌گیری بوت استرپ در علم داده به محاسبه فاصله اطمینان و آزمون آماری پرداختیم و براساس مثالی از داده‌ها، در زبان پایتون به پیاده‌سازی تکنیک بوت استرپ اقدام کردیم. همانطور که دیده شد، نتایج حاصل از برآوردگرهای بدست آمده از تکنیک بوت استرپ در علم داده با مقدارهای حاصل از روش‌های آماری تفاوت چندانی ندارند و به طور تقریبی زمانی که از توزیع آماره‌های مورد نظر اطلاعی نداریم، نتایج رضایت بخشی از بوت استرپ بدست می‌آید.