کو انرژی چیست؟ — از صفر تا صد

کو انرژی (Co-energy) دوگان انرژی است و یک کمیت فیزیکی نیست. از این کمیت در تحلیل سیستم‌هایی استفاده می‌شود که در آن‌ها انرژی ذخیره و تبدیل می‌شود. واحد کو انرژی مشابه انرژی است و به ویژه برای محاسبه نیرو‌ها و گشتاور مغناطیسی در ماشین‌های دوار کاربرد دارد.

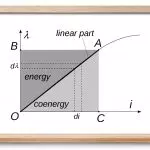
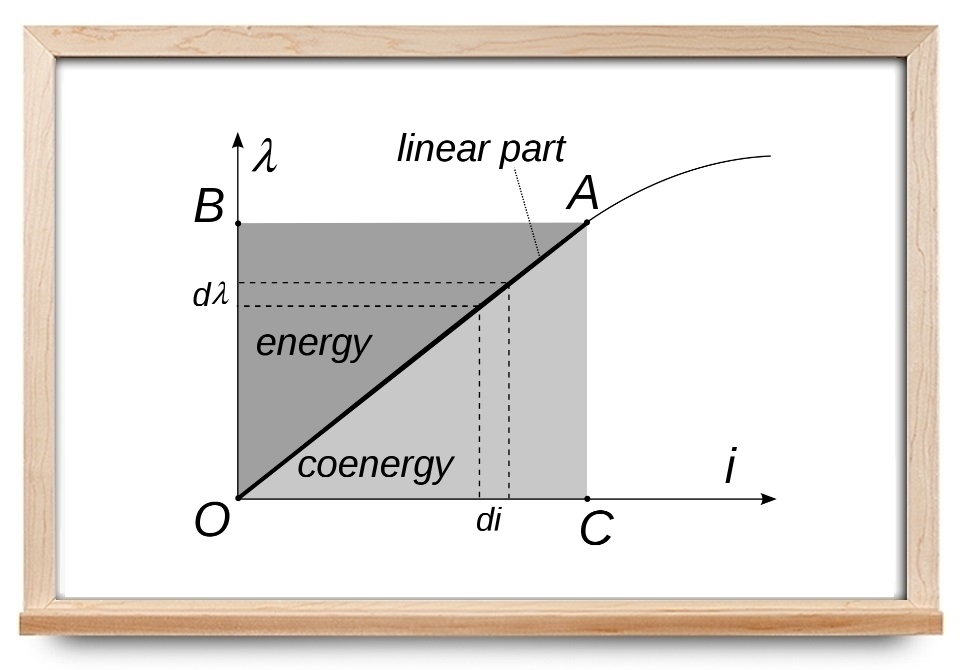
کو انرژیِ $$E'$$ (یا $$W'$$) برای سیستم‌هایی که قابلیت ذخیره انرژی ندارند برابر با صفر است. تمام انرژی که به این نوع سیستم‌ها داده می‌شود تلف شده یا به طریقی مصرف می‌شود. برای مثال، انرژی مربوط به جریان الکتریکی در یک مقاومت تلف می‌شود. اما در سیستم‌هایی که انرژی را ذخیره می‌کنند، می‌توان کو انرژی را تعریف کرد.

تعریف کو انرژی

کو انرژی در سیستم‌های الکترومغناطیسی، از تحلیل ریاضی مدار و از دیدگاه ساز و کارهای ترمودینامیکی و آماری به دست می‌آید. می‌توان به صورت ریاضی نشان داد که کو انرژی لاگرانژین (یعنی محاسبه شده با استفاده از معادله لاگرانژ) یک سیستم شامل مواد مغناطیسی و یا دی‌الکتریک است. دلیل این امر آن است که انرژی می‌تواند در در مغناطیس یا الکترواستاتیک ذخیره شود. کو انرژی را می‌توان برای محاسبه نیروی مکانیکی در سیستم‌های الکترومکانیکی با پیچه‌های حامل جریان یا آهنرباهای دائم به کار برد.

فیلم آموزش ماشین های الکتریکی 1 در فرادرس

کلیک کنید

کو انرژی مکانیکی

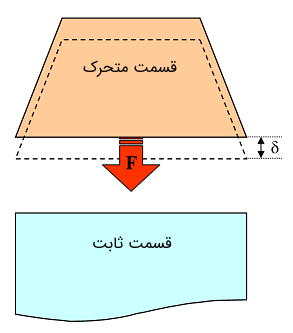
تحلیل انرژی-کوانرژی را می‌توان برای سیستم‌های دیگری که انرژی را ذخیره می‌کنند نیز به کار برد؛ برای مثال تغییر شکل الاستیکی یک فنر مکانیکی. در یک سیستم مکانیکی نمی‌توان یک نیوری لحظه‌ای به فنر اعمال کرد، زیرا این کار مستلزم تغییر شکل آنی فنر است که به نوبه خود نیازمند سرعت بی‌نهایت بوده و امری غیرممکن است.

کار $$W$$ و در نتیجه انرژی $$E$$ ذخیره شده در فنر به عنوان ضرب نیروی $$F$$ و جابه‌جایی $$x$$ فنر تعریف می‌شود ($$X$$ حداکثر جابه‌جایی فنر است.):

$$\large E _ { spring } = \int _ { 0 } ^ { X } F (x ) · d x \; \; \; \; \; (1)$$

برای یک فنر خطر ایده‌آل، نیروی $$F$$ با ضریب $$K$$ تناسب مستقیم با جابه‌جایی $$x$$ دارد:

$$\large F _ { spring } ( x ) = K · x \; \; \; \; \; (2)$$

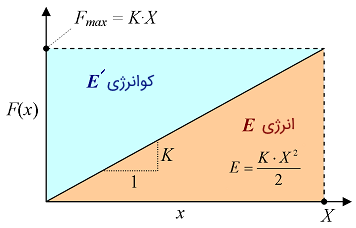
بنابراین، رابطه (۱) را می‌توان به صورت زیر بازنویسی کرد:

$$\large E _ { spring } = \int _ { 0 } ^ { X } K · x · dx = \frac { K · X ^ 2 } { 2 } \; \; \; \; \; ( 3 )$$

مفهوم انتگرال (۱) این است که به ازای تغییرات بسیار کوچک در جابه‌جایی، می‌توان نیرو را ثابت فرض کرد. بر اساس تعریف SI، «ژول مقدار کاری است که هنگام اعمال ۱ نیوتن سبب جابه‌جایی به اندازه ۱ متر می‌شود.» بنابراین، حاصل‌ضرب نیروی ثابت در مقدار جابه‌جایی، مقدار کار یا انرژی را نتیجه خواهد داد:

$$\large F · d x ~ = d W = d E \; \; \; \; \; ( 4 )$$

البته، محاسبات مشابهی را می‌توان با در نظر گرفتن جابه‌جایی ثابت و نیروی متغیر انجام داد. اما بر اساس تعریف SI، ضرب نیرو و جابه‌جایی ثابت تعریف کار نیست:

$$\large x · d F \neq dW \; \; \; \; \; ( 5 )$$

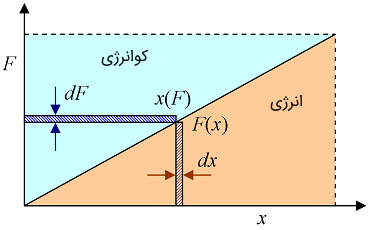
از دیدگاه فیزیکی، این مقدار کار یا انرژی نیست، اما به دلیل آنکه همان واحدها در محاسبات نقش دارند، مقدار کو انرژی نیز براساس واحدهای انرژی بیان می‌شود.

مفهوم کوانرژی در سیستم‌های غیرخطی نیز کاربرد دارد، اما در این سیستم‌ها ممکن است انرژی و کوانرژی متفاوت باشند. هرچند، با دانستن یکی از آن‌ها می‌توان دیگری را با کم کردن مقدار آن از مساحت مستطیل به دست آورد. شکل ۳ یک منحنی تنش-کرنش را برای مواد غیرخطی نشان می‌دهد که با یک رفتار الاستیک و پلاستیک ایده‌آل تقریب زده شده است.

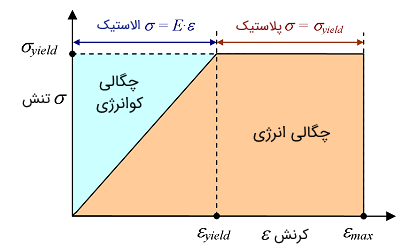
چگالی کو انرژی متناسب با انرژی است که ذخیره شده و می‌تواند به سیستم باز گردد. مقادیر تنش و کرنش (نقاط بیشینه و کمینه)‌ را می‌توان اندازه‌گیری کرد. در بخش خطی، کو انرژی برابر با انرژی ذخیره شده است و می‌توان از آن برای تخمین برگشت فنر از یک قطعه خم شده استفاده کرد. این کاربرد بسیار مفید است، زیرا بخشی از کل انرژی برای جابه‌جایی فلز استفاده می‌شود، اما از کو انرژی می‌توان برای محاسبه برگشت فنر استفاده کرد.

کو انرژی الکترومغناطیسی

در یک سیستم الکترومغناطیسی، انرژی را می‌توان در میدان الکتریکی خازن یا میدان مغناطیسی سلف ذخیره کرد. توصیف و به دست آوردن معادلات کو انرژی در مراجع مختلف معمولاً با فنر مکانیکی شکل ۴ ارائه می‌شود.

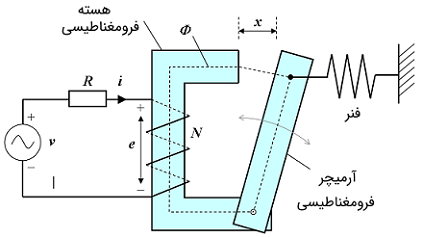
فرضیات زیر را در نظر می‌گیریم:

• مقاومت $$R$$ شامل مقاومت سلف سیم‌پیچ است. به همین دلیل، خود سیم‌پیچ بدون تلفات است.
• شار نشتی ناچیز است و در تبدیل انرژی اثری ندارد. بنابراین، اندوکتانس نشتی نیز قابل چشم‌پوشی است. این فرضیات با در نظر گرفتن فاصله هوایی کوچک است.
• هسته و آرمیچر فرومغناطیسی بدون تلفات هستند و رلوکتانس آن‌ها قابل اغماض است.
• همه شار $$\Phi$$ از $$N$$ دور سیم‌پیچ می‌گذرد، بنابراین، شار پیوندی $$\lambda$$ برابر است با:

$$\large \lambda = N · \Phi \; \; \; \; \; ( 6 )$$

آرمیچر قابل حرکت شکل ۴ را در نظر بگیرید که ثابت نگه داشته شده است. از آنجایی که سیم‌پیچ بدون تلفات است، کل انرژی الکتریکی ($$W _ e$$) که به سیستم تحویل داده می‌شود، به صورت انرژی میدان مغناطیسی (‌$$W _ f$$) ذخیره می‌گردد. اگر همه بخش‌های از نظر مکانیکی ثابت باشند (حرکت مکانیکی نداشته باشند)، آنگاه انرژی مکانیکی ($$W _ m$$) وجود نخواهد داشت:

$$\large d W _ { e } = d W _ { f } \; \; \; \; \; ( 7a )$$

$$\large d W _ { m } = 0 \; \; \; \; \; ( 7 b )$$

که در آن:

$$\large d W _ { e } = e · i · d t \; \; \; \; \; ( 8 a )$$

$$\large d W _ { f } = i · d \lambda = N · i · d \Phi \; \; \; \; \; ( 8 b )$$

کل انرژی (مساحت مثلث نارنجی شکل ۵) را می‌توان با انتگرال‌گیری تابع در بازه مناسب محاسبه کرد:

$$\large \Delta W _ f = \int _ { \lambda _ 1 } ^ { \lambda _ 2 } i ( \lambda ) · d \lambda \; \; \; \; \; ( 9 )$$

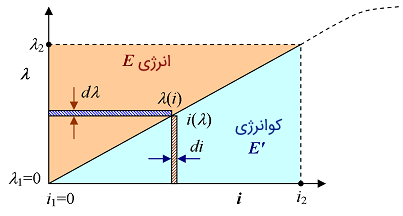
البته به جای شار پیوندی $$\lambda$$ می‌توانیم از جریان $$i$$ نیز به عنوان متغیر مستقل استفاده کنیم و در نتیجه، ناحیه مکمل کوانرژی (مثلث آبی شکل ۵) را به صورت زیر محاسبه کنیم:

$$\large \Delta W' _ f = \int _ { i _ 1 } ^ { i _ 2 } \lambda ( i ) · d i \; \; \; \; \; ( 10 )$$

مساحت کل مستطیل برابر با مجموع مساحت‌های دو مثلث است. بنابراین، می‌توان نوشت:

$$\large \Delta W _ f + \Delta W' _ f = \lambda · i \; \; \; \; \; ( 1 1 )$$

و در نتیجه، انرژی (و کو انرژی) ذخیره شده برابر با نصف مساحت مستطیل است:

$$\large \Delta W _ f = \frac { \lambda · i } { 2 } \; \; \; \; \; ( 1 2 )$$

انرژی $$W _ f$$ تابعی از دو متغیر مستقل $$\lambda$$ و $$x$$ است (اندوکتانس $$L (x)$$ تابعی از $$x$$ است):

$$\large W _ f ( \lambda , x ) = \frac { 1 } { 2 } · \frac { \lambda ^ 2 } { L ( x ) } \; \; \; \; \; ( 1 3 )$$

کو انرژی $$W'_f$$ نیز تابعی از دو متغیر مستقل $$i$$ و $$x$$ است:

$$\large W' _ f ( i , x ) = \frac { 1 } { 2 } · { L ( x ) } · i ^ 2 \; \; \; \; \; ( 1 4 )$$

معادلات (۱۳) و (۱۴) توصیف عمومی انرژی و کو انرژی در سیستم‌های مغناایستایی هستند (طبق فرضیاتی که قبلاً بیان کردیم).

جهت نیرویی که در هر نیروی مکانیکی که در چنین سیستمی برقرار می‌شود، به گونه‌ای است که کوانرژی را افزایش داده و انرژی ذخیره شده میدان را کاهش می‌دهد. نیرو گرادیانی از کو انرژی است (با علامت منفی).

کو انرژی در سیستم غیرخطی

انرژی و کو انرژی فقط در سیستم‌های کاملاً خطی و بدون تلفات با هم برابر هستند. اما در عمل، سیستم‌ها غیرخطی هستند، مخصوصاً اگر اشباع مغناطیسی رخ دهد. همان‌گونه که در شکل ۶ نشان داده شده است،‌ به دلیل غیرخطی بودن، مقادیر انرژی و کو انرژی را باید با انتگرال‌های مناسب محاسبه کرد (معادلات (۹) و (۱۰)). در این حالت، دیگر انرژی برابر با کو انرژی نیست، در نتیجه: $$W \neq W'$$ یا $$E \neq E'$$.

البته این گفته همیشه برای سیستم‌های خطی و غیرخطی درست است که مجموع انرژی و کوانرژی برابر با مساحت مشخص شده مستطیل است:

$$\large E + E' = \lambda · i \; \; \; \; \; ( 1 5 )$$

همان‌گونه که در شکل ۶ نشان داده شده است، با شروع اشباع، افزایش انرژی نیز متوقف می‌شود (ناحیه نارنجی)، در حالی که کوانرژی با افزایش جریان زیاد می‌شود.

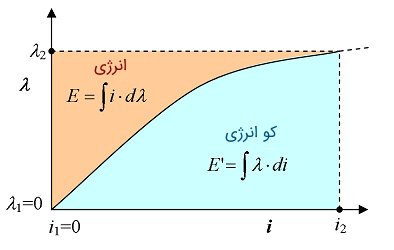
در اینجا، نباید از معادلات عمومی نیرو و کوانرژی استفاده کرد. این معادلات را باید برای هر مورد خاص به دست آورد تا اطمینان حاصل شود که قوانین اساسی فیزیک، مانند پایستگی انرژی، برقرار هستند.

سیستم‌‌های دوار و با تحریک چندگانه

نیرو و گشتاور سیستم‌هایی با چند منبع تحریک (مانند ماشین‌های سه‌فاز) را نیز می‌توان با کو انرژی محاسبه کرد. تحلیل‌ها و روابط به چنین سیستم‌هایی قابل تعمیم هستند. در نتیجه، نیرو یا گشتاور $$T$$ تابعی از همه جریان‌های تحریک و موقعیت زاویه‌ای یا زاویه $$\theta$$ است. برای مثال:

$$\large T = \frac { \partial W' \left ( i _ 1 , i _ 2 ... i _ n , \theta \right ) } { \partial \theta} \; \; \; \; \; ( 1 6 )$$

کو انرژی الکترواستاتیکی

سیستم‌های الکترواستاتیکی قابلیت ذخیره انرژی در میدان الکتریکی را دارند. بنابراین، تحلیل کوانرژی را می‌توان به طریق مشابهی با سیستم‌های بالا برای آن‌ها انجام داد.

کاربردهای کو انرژی

در این بخش، چند مورد را بیان می‌کنیم که کو انرژی در محاسبه روابط آن‌ها کاربرد دارد.

فیلم آموزش مبانی مهندسی برق 1 در فرادرس

کلیک کنید

روش اجزای محدود

در ماشین‌های الکتریکی (موتورها و ژنراتورها) و سایر دستگاه‌ها (فعال‌گرها و رله‌ها)، محاسبه رابطه بین نیروی مکانیکی و جریان الکتریکی (یا میدان مغناطیسی یک آهنربای دائم) موضوع مهمی است. اگر در چنین محاسباتی انرژی ذخیره شده به عنوان پایه در نظر گرفته شود، عکس کردن رابطه بین شار پیوندی و جریان از نظر ریاضی دشوار خواهد بود، مخصوصاً در سیستم‌های واقعی که ممکن است فرم جبری ساده‌ای وجود نداشته باشد. البته با استفاده از روش کو انرژی تنها کافی است مشتق جزئی نسبت به جابه‌جایی را برای به دست آوردن تابع نیرو محاسبه کنیم.

این ویژگی را می‌توان برای مثال در مدل‌سازی روش اجزای محدود (FEM) برای یافتن نیرو و گشتاور اعمالی بر بخش مورد نظر به کار برد. بسیاری از روش‌های دیگر (معادله نیروی لورنتس، نرخ تغییر انرژی میدان، تانسور تنش ماکسول) نیز وجود دارند، اما از روش کو انرژی نیز می‌توان استفاده کرد. یکی از مزایای استفاده از روش کو انرژی این است که با استفاده از آن، محاسبه نیروها برای اجزایی که به سایر بخش‌های مغناطیسی متصل هستند ممکن می‌شود.

برای یک حجم مشخص میدان مغناطیسی، کو انرژی را می‌توان به صورت زیر محاسبه کرد:

$$\large W' = \int _ V \left ( \int ^ H _ 0 B ( H ) d H \right ) d V \; \; \; \; \; ( 1 7 )$$

برای محاسبه نیرو از کوانرژی، جریان‌ها ثابت نگه داشته شده و موقعیت هر شیء برای اعمال نیرویی که باید محاسبه شود، کمی آشفته شده است. نیرو را می‌توان با محاسبه مشتق جزئی کو انرژی نسبت به جابه‌جایی $$\delta$$ (نسبت به موقعیت اولیه $$p$$) تخمین زد:

$$\large F = \frac { W' ( p + \delta ) - W' ( p ) } { \delta } \; \; \; \; \; ( 1 8 )$$

مؤلفه نیرو برای جهتی که در آن اغتشاش اعمال شده است، ارزیابی می‌شود. بنابراین، محاسبه دو بار برای مسائل دوبعدی (برای مثال در جهت‌های $$x$$ و $$y$$) یا سه بار برای مسائل سه‌بعدی ($$x$$، $$y$$ و $$z$$) انجام می‌شود. جهت جابه‌جایی می‌تواند دلخواه باشد، اما اغلب در امتداد مرجع اصلی محورها انجام می‌شود. این تکنیک محاسبه نیرو را اغلب روش جابه‌جایی مجازی (Virtual Displacement Method) یا روش کار مجازی (Virtual Work Method) می‌نامند.

سیستم دوار با تحریک تکی

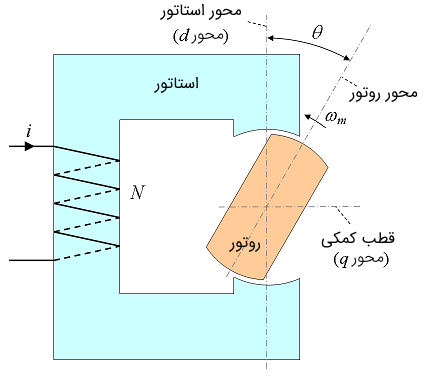
یک سیستم دوار با تحریک تکی را در نظر بگیرید که در شکل ۸ نشان داده شده است. یک جریان سینوسی به سیم‌پیچی استاتور اعمال شده و روتور آزادانه روی شفت می‌چرخد. گشتاور گشترش یافته $$T$$ را می‌توان از متغیرهای $$i$$ و $$\theta$$ و با معادله زیر محاسبه کرد:

$$\large i ( t ) = I · \sin ( \omega · t ) \; \; \; \; \; ( 1 9 )$$

فیلم آموزش مبانی مهندسی برق ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

لازم به ذکر است که فرکانس جریان استاتور ($$\omega$$) با فرکانس چرخش مکانیکی ($$\omega _ m$$) متفاوت است.

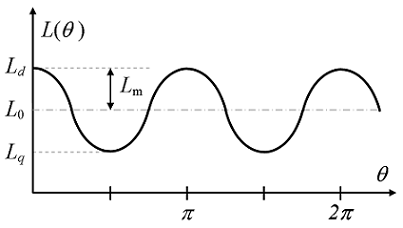
رلوکتانس تابعی از موقعیت روتور است و به دلیل تقارن، دو چرخه رلوکتانس در یک چرخش کامل روتور وجود دارد. در این حالت خاص، رلوکتانس و در نتیجه تغییرات اندوکتانس را می‌توان با تابع ساده زیر توصیف کرد (شکل ۹):

$$\large L ( \theta ) = L _ 0 + L _ m · \cos ( 2 · \theta ) \; \; \; \; \; ( 20 )$$

به دلیل وجود یک فاصله هوایی نسبتاً قابل توجه، سیستم خطی بوده و کو انرژی (که در این حالت برابر با انرژی است) از معادله زیر محاسبه می‌شود:

$$\large W' = \frac { 1 } { 2 } · { L ( \theta ) } · i ^ 2 \; \; \; \; \; ( 21 )$$

سپس گشتاور $$T_d$$ (برای محور $$d$$ در شکل ۸) را می‌توان با جایگذاری معادله (۲۱) در (۱۶) محاسبه کرد:

$$\large T _ d = \frac { \partial W' \left ( i, \theta \right ) }{ \partial \theta } = \frac { 1 } { 2 } · i ^ 2 · \frac { \partial L ( \theta ) } { \partial \theta } \; \; \; \; \; ( 2 2 )$$

و با استفاده از تابع معلوم اندوکتانس (معادله (۲۰) و معادله جریان (۱۹))، داریم:

$$\large T _ d = - I ^ 2 · L _ m · \sin ( 2 · \theta ) · \sin ^ 2 ( \omega · t ) \; \; \; \; \; ( 2 3 )$$

فرض بر این است که روتور در سرعت زاویه‌ای $$\omega _ m$$ می‌چرخد (شکل ۸). بنابراین، داریم:

$$\large \theta = \omega _ m · t - \delta \; \; \; \; \; ( 2 4 )$$

در لحظه $$t = 0$$، با تعریف معادله (۱۹)، رابطه $$i = 0$$ را داریم. در نتیجه، موقعیت روتور برابر است با:

$$\large\theta = - \delta \; \; \; \; \; ( 2 5 )$$

بنابراین، معادله (۲۳) را می‌توان با اتحادهای مثلثاتی برای $$\sin ^ 2 ( x )$$ و $$\sin ( y ) · \sin ( z )$$ بازنویسی کرد:

$$\large T _ d = - \frac { I ^ 2 · L _ m } { 2 } · \left ( \sin \{ 2 · ( \omega _ m · t - \delta ) \} - \frac { \sin \{2 · [ ( \omega _ m + \omega ) · t - \delta ] \} } { 2 } - \frac { \sin \{ 2 · [ ( \omega _ m - \omega ) · t - \delta ] \} } { 2 } \right ) \; \; \; \; \; ( 2 6 )$$

مقدار میانگین یک تابع سینوسی برابر با صفر است. تنها حالتی که $$T_{d,avg}$$ صفر نیست، برابری دو فرکانس ($$\omega_m = \omega$$) است:

$$\large T _ { d , a v g} = - \frac { I ^ 2 · L _ m } {4 } · \sin ( 2 · \delta ) \; \; \; \; \; ( 2 7 )$$

از شکل ۹ مشخص است $$L _ m$$ دامنه تغییرات اندوکتانس است که در این حالت، به صورت زیر محاسبه می‌شود:

$$\large L _ m = \frac { L _ d - L _ q } { 2 } \; \; \; \; \; ( 2 8 )$$

بنابراین، گشتاور گسترش یافته میانگین برای این حالت خاص به صورت زیر خواهد بود:

$$\large T _ { d , a v g } = - \frac { I ^ 2 · ( L _ d - L _ q ) }{ 8 } · \sin ( 2 · \delta ) \; \; \; \; \; ( 2 9 )$$

محاسبات مشابهی را می‌توان برای یک سیستم دوار با تحریک چندگانه نیز انجام داد، اما همه جریان‌ها و اندوکتانس‌ها (همچنین اندوکتانس‌های متقابل) را باید در محاسبات در نظر گرفت.

سیستم مغناطیس دائم

مقادیر انرژی/کوانرژی در سیستم‌هایی با آهنربای دائم را نمی‌توان تنها با جریان‌ها ارتباط داد، زیرا مقداری انرژی در آهن‌رباها ذخیره شده است. البته همچنان می‌توان نیروها را با استفاده از روش کوانرژی محاسبه کرد، اما به دلیل حضور مغناطیس‌های دائم، باید مدل‌های ریاضیاتی را برای در نظر گرفتن اطلاعاتی درباره شارهای پیوندی اصلاح کرد. یک مغناطیس دائم را می‌توان با یک سیم‌پیچی معادل نمایش داد.

با استفاده از این روش، می‌توان منحنی مغناطیس‌زدایی مربوطه را از ربع دوم به ربع اول منتقل کرد و چگالی کو انرژی (یا چگالی انرژی) را بر اساس آن محاسبه کرد. این تغییر با اعمال یک آفست به همه مقادیر متناظر $$H$$ انجام می‌شود.

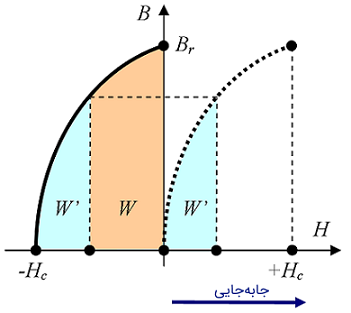
مدل‌سازی حلقه B-H

حلقه هیسترزیس مواد فرومغناطیس را می‌توان با مدل Jiles–Atherton (مدل J-A) تقریب زد. اتلاف انرژی ماده متناسب با مساحت حلقه B-H است. ناحیه محصور بین منحنی B-H و محور B انرژی است (مشابه شکل ۶)، در حالی که ناحیه محصور بین منحنی B-H و محور H، کو انرژی را نشان می‌دهد. مدل J-A مبتنی بر محاسباتی مشابه کو انرژی است.

مساحت حلقه B-H در هر دو حالت (محاسبه شده از طریق انرژی یا کو انرژی) برابر است. البته، مقادیر لحظه‌ای انتگرال‌ها با هم برابر نیست که ممکن است منجر به خطاهای کوچکی در پیش‌بینی شکل حلقه شود؛ حتی اگر مساحت کل پیش‌بینی شده با دقت بهتری همراه باشد.

اگر به یادگیری مباحث مشابه این مطلب علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• اصول عملکرد ترانسفورماتور — به زبان ساده
• مدارهای مغناطیسی — به زبان ساده
• کنترل موتورهای الکتریکی — به زبان ساده

^^