پس آزمون یا آزمون تعقیبی در تحلیل واریانس | به زبان ساده
«پس آزمون» یا «آزمون تعقیبی» (Post-Hoc) یک بخش جدایی ناپذیر از تحلیل واریانس یا همان ANOVA است. وقتی از ANOVA برای آزمون برابری حداقل سه گروه استفاده میکنید، «معنیدار آماری» (Statistical Significant) به این معنی است که میانگین همه گروهها برابر نیستند. با این حال، نتایج حاصل از آزمون یا جدول ANOVA مشخص نمیکند که تفاوتهای مورد نظر، مختص کدام جفت از گروهها است. تشخیص تفاوت بین گروههای مختلف، با کنترل میزان خطای آزمون آماری، به عهده روشهایی به نام پس آزمون یا آزمون تعقیبی در تحلیل واریانس است.


به منظور کسب اطلاعات بیشتر در مورد آزمون و تحلیل واریانس بهتر است نوشتارهای تحلیل واریانس (Anova) — مفاهیم و کاربردها و استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن مطالب تحلیل واریانس اندازه مکرر یک طرفه در SPSS | راهنمای گام به گام و آزمون لون (Levene’s Test) برای برابری واریانس ها در SPSS — راهنمای کاربردی نیز خالی از لطف نیست.
پس آزمون یا آزمون تعقیبی در تحلیل واریانس
در این متن، به شما نشان خواهیم داد که تحلیلهای پس آزمون یا آزمون تعقیبی (Post-Hoc Analysis) چیست و مزایای اساسی استفاده از آنها در کجا نهفته شده است. این امر بخصوص در تحلیل واریانس (Analysis of Variance) که یک آزمون تحلیلی کلینگر است، اهمیت پیدا میکند.
در بخش اول نوشتار با معرفی نحوه عملکرد آنالیز واریانس پرداخته و ضعفهای آن را مشخص میکنیم. آنگاه در ادامه، مفهوم پس آزمون یا آزمون تعقیبی بخصوص در تحلیل واریانس روشنتر شده و بهتر میتوانید از میان انواع مختلف روشهای اجرای پس آزمون، مناسبترین را برای تحلیل آماری خود، انتخاب کنید. همچنین مشخص خواهد شد که چرا عدم کنترل میزان خطای آزمون آماری، باعث میشود که در مورد نتایج حاصل از تحلیلها و مقایسههای دوتایی دچار تردید و شک شوید.
آزمون تحلیل کلینگر
به طور معمول، وقتی میخواهید تعیین کنید که سه یا چند گروه با هم متفاوت هستند، از شاخص آماری مرکزی مانند میانگین برای مقایسه استفاده کرده و تحلیل یا آنالیز واریانس (ANOVA) را اجرا خواهیم کرد. آمارشناسان از آزمون F در جدول تحلیل واریانس به عنوان یک آماره آزمون استفاده میکنند و چنین روشی را آزمون تحلیل کلینگر (Omnibus ANOVA) مینامند.
البته آزمون ولچ (ANOVA Welch) در طرح تحلیل واریانس، نوع دیگری از آزمایش کلینگر محسوب میشود که شرایط اجرای آنالیز واریانس را سهلتر میکند. در تحلیل واریانس کلینگر، شرط برابری واریانسها در بین هر گروه یا تیمار (Treatment) وجود دارد، در حالیکه آزمون ولچ این شرط را کمرنگتر کرده است.
منظور از اصطلاح «کلینگر» (Omnibus)، آن است که آزمون تحلیل واریانس، همه میانگینها را به صورت یک کل، مورد بررسی قرار میدهد و به جزئیات یا مقایسههای دوتایی یا زوجی از گروهها نمیپردازد. به بیان دیگر آزمون کلینگر، نتایج کلی را برای دادههای شما ارائه میدهد و فقط قادر است به پرسشی به صورت «آیا تفاوت بین میانگین آماری گروهها معنی دار است بله یا خیر؟» پاسخ بدهد. قاعده تصمیم برای چنین آزمونی براساس مقدار احتمال صورت میگیرد. اگر «مقدار احتمال» (p-value) کمتر از میزان احتمال خطا یا سطح آزمون باشد، فرض صفر را رد میکنیم. همچنین طبق آماره آزمون F یا «آماره ولچ» نیز فقط میتوانیم پرسش مطرح شده را پاسخ داده و نسبت به رد فرض صفر تصمیم بگیریم.
فرضیههایی که در این تحلیل واریانس کلینگر مورد بررسی قرار میگیرند به صورت زیر نوشته میشوند.
- فرض صفر: همه میانگین گروهها برابر هستند.
- فرض مقابل: همه میانگینها برابر نیستند.
واضح است که نتایج آزمون ANOVA مشخص نمیکند که کدام گروه یا گروهها با سایر گروهها به طور آماری، متفاوت هستند. همانطور که از فرضهای آماری گفته شده بر میآید، اگر فرض صفر رد شود، فقط میدانیم که همه میانگینها برابر نیستند. ولی در بعضی از اوقات لازم است ریشه این نابرابری را پیدا کنیم و مشخص کنیم که کدام گروه یا گروهها با گروههای دیگر تفاوت چشمگیری یا اختلاف آماری دارند.
تحلیل واریانس یک طرفه برای استفاده از پس آزمون یا آزمون تعقیبی
از این بخش به بعد، با معرفی یک مثال، جنبههای مختلف آزمون یا تحلیل واریانس یک طرفه به همراه پس آزمون یا آزمون تعقیبی را مورد بررسی قرار داده و نتایج حاصل را تفسیر میکنیم. برای دسترسی به فایل اطلاعاتی به کار رفته در این قسمتها، اینجا کلیک کنید تا فایل با قالب فشرده PostHocTests را دریافت کنید. پس از خارج کردن فایل از حالت فشرده، میتوانید آن را در محیط Excel باز کرده و دادهها را مشاهده کنید. در تصویر ۱، دادههای مربوط به این فایل را مشاهده میکنید.
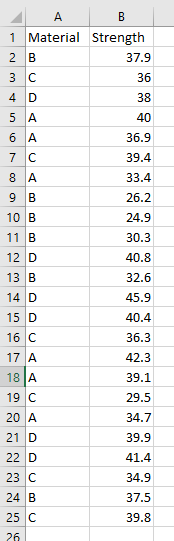
همانطور که در تصویر ۱، دیده میشود، در ستون اول «نوع ماده» (Material) با حروف A تا D مشخص شده است. از طرفی، ستون دوم «مقاومت» (Strength) هر یک از مواد را در مقابل فشار عمودی، مشخص کرده است. میخواهیم بدانیم، آیا نوع ماده در مقاومت آنها در مقابل فشار عمودی، موثر است یا همه مواد، مقاومت یکسانی نسبت به آن دارند.
ابتدا به بررسی میانگینها به عنوان شاخص تمرکز و انحراف استاندارد به عنوان شاخص پراکندگی برای هر یک از گروه مواد میپردازیم. البته برای میانگین هر کدام نیز یک فاصله اطمینان ۹۵٪ (CI) تهیه کردهایم. نتیجه این محاسبات را در تصویر ۲ مشاهده میکنید.
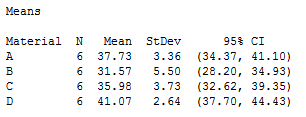
نکته: این گونه تحلیل یا شاخصها را به کمک بیشتر نرمافزارهای محاسبات آماری میتوانید انجام دهید. برای مثال تحلیل واریانس در محیط برنامهنویسی R در نوشتار آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی مورد بررسی قرار گرفته است.
نتیجه اجرای تحلیل واریانس برای چنین دادههایی در تصویر 3 دیده میشود. جدول «تحلیل واریانس یک طرفه» (One-way Anova) بیانگر وجود اختلاف در بین میانگینها است، زیرا مقدار احتمال در جدول آنالیز واریانس کمتر از خطای نوع اول است. مشخص است که است.
در نتیجه فرض صفر که به صورت برابری میانگینهای مقاومت چهار نوع ماده در مقابل فشار عمودی بیان شده، رد میشود. پس حداقل یکی از میانگینها با بقیه متفاوت است. متاسفانه آزمون کلینگر، نمیتواند مشخص کند که این ماده، کدام یک از مواد A تا D است.

برای مقایسه میانگین زوج گروهها، باید پس آزمون یا آزمون تعقیبی را پس از انجام تحلیل واریانس و به شرط رد شدن فرض صفر، اجرا کرد. چنین کاری را به عنوان «مقایسههای چندگانه» (Multiple Comparison) نیز میشناسند. در لاتین چنین کاری به اصطلاح، post hoc به معنای «پس از این» گفته میشود. به همین دلیل پس آزمون یا آزمونهای تعقیبی در نرمافزارهای آماری به نام Post Hoc معروفند.
قبل از اینکه به بررسی پس آزمون یا آزمون تعقیبی بپردازیم، در مورد خطای آزمون باید توضیحاتی ارائه کنیم تا مشخص شود چرا نباید «آزمون زوجی» (Paired-wise Comparison) یا «آزمونهای تی-دو نمونه مستقل» (Two Independent Sample T Test) را به طور مجزا برای هر جفت گروه انجام دهیم.
نرخ خطای آزمون چیست؟
پس آزمون یا آزمون تعقیبی دو کار مهم را انجام میدهند.
- آزمون مقایسه چندگانه
- کنترل خطای آزمونها
همانطور که اشاره کردیم، یکی از وظایف مهم پس آزمونها، تعیین گروه یا گروههایی است که با دیگر گروهها، تفاوت معنیداری دارند. ممکن است بپرسید که این کار را به کمک آزمون t دو گروه مستقل یا دو گروه وابسته نیز میتوان انجام داد. در اینجا است که وظیفه دوم پس آزمون یا آزمون تعقیبی مشخص میشود. آنها نرخ یا احتمال خطای آزمون را کنترل میکنند.
ولی واقعا نرخ خطای آزمون چیست؟ برای هر آزمون فرضی که انجام میدهید، یک میزان خطای نوع اول وجود دارد که سطح آزمون یا «میزان با معنایی» () را تعریف میکند. به عبارت دیگر، این احتمال وجود دارد که شما فرض صفر را به اشتباه رد کنید، چنین امری را «کاذب مثبت» (False-Positive) مینامند.
هنگامی که فقط یک آزمون مورد نظر است، میزان خطای نوع اول، اغلب 5٪ در نظر گرفته میشود. با این حال، هرچه آزمونهای بیشتری انجام شود، احتمال مثبت کاذب افزایش مییابد. به این ترتیب میزان خطا برای یک خانواده از آزمونها (اگر به صورت همزمان اجرا شوند) همیشه بیشتر از خطای نوع اول برای تک آزمونها خواهد بود.
تصور کنید که یک جفت تاس را ریختهاید و خطای نوع اول، مشاهده عدد یک در هر دو تاس باشد. این احتمال (احتمال خطای نوع اول) برابر است با:
به این موضوع توجه داشته باشید که پرتاب یک تاس و مشاهده عدد یک با احتمال رخ میدهد. ولی هرچه تعداد پرتاب تاسها را بیشتر کنیم، احتمال مشاهده دو عدد یک بیشتر خواهد شد. برای مثال فرض کنید که در ۲۵ پرتاب، میخواهیم احتمال مشاهده حداقل دو عدد یک را محاسبه کنیم.
یا
به این ترتیب مشاهده عدد جفت یک، سه تا یک، چهار تا یک و ... در پرتاب ۲۵ تاس، تقریبا ۵۰ درصد است.
نرخ خطای آزمونها در ANOVA
در تحلیل ANOVA، میخواهیم میانگین گروه را با یکدیگر مقایسه کنیم. هرچه گروههای بیشتری برای مقایسه داشته باشید، آزمونهای مقایسهای بیشتری برای استنباط گروههای نامساوی لازم است. برای مثال ANOVA با چهار گروه (A B C D) را در نظر بگیرید. برای مقایسههای دو به دو احتیاج به شش مقایسه مجزا خواهیم داشت.
- A – B
- A – C
- A – D
- B – C
- B – D
- C – D
متأسفانه، همانطور که در ادامه متن مشاهده خواهید کرد، خطاهای آزمون به طور فزایندهای، تغییر میکند. این موضوع باعث افزایش نرخ خطای آزمون شده و نتایج حاصل از آزمون را بیاعتبار میسازد. جدول زیر نشان میدهد که چگونه افزایش تعداد گروه های مورد نظر، باعث افزایش تعداد مقایسهها و به نوبه خود، باعث افزایش خطای آزمون میشود. توجه کنید که با افزودن فقط چند گروه، چقدر سریع مقایسهها افزایش پیدا کرده و خطای آزمایش به سرعت مشکل ساز میشود. جدول با دو گروه شروع میشود و مقایسه تکی بین دو گروه با خطای ۵٪ همراه است.
جدول ۱: مقایسههای مجزا براساس مقدار برای هر آزمون زوجی
| گروهها | تعداد مقایسههای دو تایی | خطای مقایسههای مجزا |
| 2 | 1 | 0٫05 |
| 3 | 3 | 0٫0142625 |
| 4 | 6 | 0٫401263061 |
| 5 | 10 | 0٫53670877 |
| 6 | 15 | 0٫53670877 |
| 7 | 21 | 0٫659438374 |
| 8 | 28 | 0٫7621173115 |
| 9 | 36 | 0٫842220785 |
| 10 | 45 | 0٫900559743 |
| 11 | 55 | 0٫940461445 |
| 12 | 66 | 0٫966134464 |
| 13 | 78 | 0٫981700416 |
| 14 | 91 | 0٫990606054 |
| 15 | 105 | 0٫995418807 |
بهتر است ابتدا با نحوه محاسبات در این جدول بیشتر آشنا شویم. ابتدا به بررسی ستون مربوط به تعداد مقایسههای دو تایی میپردازیم. تعداد ترکیبهای دوتایی از مشاهده به صورت زیر است.
برای مثال برای ۱۰ گروه، تعداد مقایسههای دو تایی به صورت زیر قابل محاسبه است.
علاوه بر این، فرمول محاسبه نرخ خطا برای کل مجموعه مقایسهها، مطابق با که در آن سطح خطای آزمون تکی و تعداد مقایسهها است.
باز هم برای مثال اگر تعداد ۱۰ گروه وجود داشته باشد، با توجه به اینکه تعداد مقایسه زوجی برابر با ۴۵ خواهد بود، خطای کل آزمونها به شکل زیر بدست میآید.
از آنجایی که در مثال مورد نظر ما برای تحلیل واریانس چهار گروه وجود دارد، شش مقایسه زوجی باید صورت بگیرد که خطای نوع اول همه آنها برابر با 0٫26 است. بنابراین باید کاری کرد که میزان خطا قابل کنترل باشد.
کنترل خطای پس آزمونها
در جدول 1، به طور خلاصه به مشکل افزایش خطای آزمون اشاره کردیم. حال باید به راه حل این موضوع بپردازیم.
هنگام انجام تجزیه و تحلیل آماری، انتظار داریم میزان خطای آزمونها یا نرخ مثبت کاذب، برابر با 5٪ بوده یا هر مقدار دلخواهی باشد که برای سطح اهمیت تعیین کردهایم.
همانطور که در جدول ۱، مشاهده میشود، هنگامی که تعداد گروهها را از 2 به 3 افزایش میدهیم، میزان خطا تقریباً سه برابر شده و از 0٫05 به 0٫143 میرسد
اگر برای مقایسه سیستماتیک تمام گروها از «آزمونهای تی-دو نمونه مستقل» (Two Independent Sample T Test) استفاده میکردیم، با مشکل افزایش خطای آزمون یا نرخ مثبت کاذب مواجه میشدیم.
خوشبختانه، پس آزمون یا آزمون تعقیبی راهحل مناسبی برای مواجه با این مشکل است. در ادامه به معرفی چند تکنیک و روش برای به کارگیری پس آزمون یا آزمون تعقیبی خواهیم پرداخت.
روش توکی برای تحلیل واریانس یک طرفه
براساس مثالی که برای تحلیل واریانس (ANOVA) اجرا کردیم، مشخص است که چهار گروه وجود دارد که برای مقایسههای زوجی به ۶ آزمون مجزا احتیاج داریم. به کمک «روش ترکی» (Tukey's Method)، آزمونهای مقایسهای زوجی را به شکلی اجرا میکنیم که نرخ خطای نوع اول این خانواده از آزمونها از ۰٫۰۵ تجاوز نکند.
البته تکنیکهای مختلفی برای مقایسههای دو تایی در تحلیل واریانس وجود دارد، ولی روش توکی، محبوبترین و عمومیترین روش برای مقایسههای زوجی در پس آزمون یا آزمون تعقیبی محسوب میشود.
برای بیان نتایج حاصل از پس آزمون یا آزمون تعقیبی دو رویکرد وجود دارد. در روش اول از «مقدار احتمال اصلاح شده» (Adjusted p-values) استفاده شده و در روش دوم از «فاصلههای اطمینان همزمان» (Simultaneous Confidence Intervals) بهره گرفته میشود.
در ادامه این متن هر یک از این تکنیکها را بازگو خواهیم کرد.
مقدار احتمال اصلاح شده
به تصویر 4 توجه کنید. ستون آخر جدول در این تصویر، نشانگر «مقدار احتمال اصلاح شده» (Adjusted P-Value) برای مقایسههای دو تایی از اختلاف بین مقادیر زوج گروهها است.
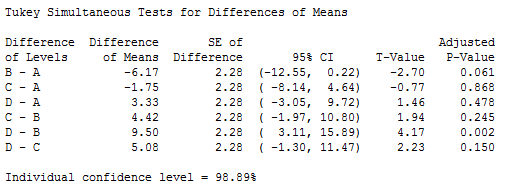
هر یک از مقادیر احتمال اصلاح شده در این جدول، بیانگر سطح معنیداری برای اختلاف بین دو گروه است، بطوری که نرخ خطای خانواده آزمونها از نرخ خطای نوع اول فراتر نمیرود. اگر مقدار احتمال از میزان خطای نوع اول (که معمولا ۰٫۰۵ در نظر گرفته میشود) در هر یک از این آزمونها کوچکتر باشد، فرض برابری برای آن زوج، رد میشود. در صورتی که برعکس مقدار احتمال از میزان خطای نوع اول، بزرگتر باشد، نمونه جمعآوری شده، دلیلی بر رد برابری این زوج ارائه نمیکند.
نکته: توجه داشته باشید که مقدار خطای نوع اول برای این خانواده از آزمونها (آزمون تعقیبی) برابر با ۰٫۰۵ خواهد بود.
با توجه به تصویر 4، مشخص است که اختلاف بین دو گروه A و B به میزان 6٫17- وجود دارد. ولی این اختلاف از لحاظ آماری، معنیدار نیست زیرا مقدار احتمال اصلاح شده، بیشتر از ۰٫۰۵ است. ولی بین دو گروه B و D میزان اختلاف برابر با ۹٫۵۰ است که با توجه به مقدار احتمال اصلاح شده (۰٫۰۰۲) اختلاف معنیداری بین آنها از لحاظ آماری وجود دارد. به نظر میرسد وجود این زوج، باعث رد فرض صفر در تحلیل واریانس یک طرفه بوده است.
فاصله اطمینانهای همزمان
همانطور که گفته شد، روش دیگر برای اجرای پس آزمون یا آزمون تعقیبی به کمک فاصلههای اطمینان همزمان، صورت میپذیرد. این فاصله اطمینانها برای اختلاف بین میانگین گروهها تشکیل میشود.
به یاد دارید که آزمون فرض آماری دو طرفه با اندازه مترادف با یک فاصله اطمینان است. برای مثال یک آزمون با اندازه یا سطح خطای ۰٫۰۵ درست به مانند یک فاصله اطمینان ۹۵٪ برای مقایسه بین میانگینها، عمل میکند.
در پس آزمون یا آزمون تعقیبی نیز فاصله اطمینان همزمان برای خانوادهای از آزمونها به کار رفته و نتیجهای مانند آزمون با مقدار احتمال اصلاح شده خواهد داشت. منظور از فاصله اطمینان همزمان، فاصلههایی است که همگی آنها با اطمینان ۹۵٪ شامل میانگین (یا اختلاف میانگین) گروهها است. به این ترتیب پس آزمونهای با سطح خطای ۵٪ مشابه با فاصله اطمینان همزمان ۹۵٪ است.
این فاصلههای اطمینان همزمان را در جدول مربوط به تصویر 4 نیز مشاهده میکنید. کافی است به ستون فاصله اطمینان (Confidence Interval) یا CI با ۹۵٪ توجه کنید. اگر میانگین دو گروه اختلاف معنیداری نداشته باشند، فاصله اطمینان همزمان آنها شامل نقطه صفر خواهد بود. باز هم بر همین اساس مشخص است که فقط بین دو گروه B و D این فاصله فقط شامل مقادیر مثبت شده است. ولی بقیه فاصلهها در کران پایین، منفی و در کران بالا، مثبت هستند. در نتیجه فرض برابری میانگین در بین این دو گروه رد میشود.
برای روشنتر شدن موضوع به تصویر 5 توجه کنید. در این نمودار، هر یک از فاصلههای اطمینان برای اختلاف میانگین گروهها ترسیم شده است. واضح است که فقط اختلاف برای گروه D و B از خط صفر (خط نقطه چین عمودی در مرکز نمودار) فاصله دارند.
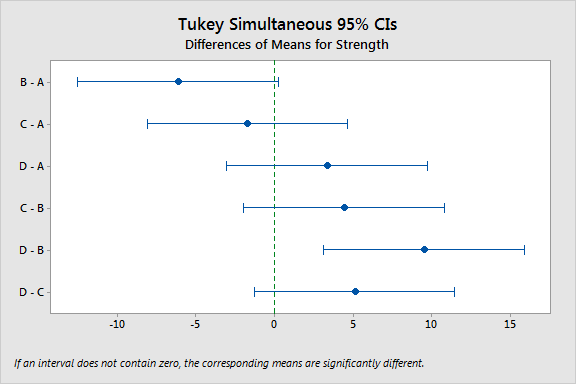
نمودار موجود در تصویر 5، میتواند برای مقایسه میانگین جامعههای آماری نیز به کار رود. در حقیقت این خطوط، اختلاف میانگین هر زوج از جامعهها را در بر میگیرند. زمانی که طول فاصله یا بازه اطمینان، بزرگ باشد، دقت در برآورد میانگین یا اختلاف میانگین کم میشود. البته به یاد داشته باشید که اگر درصد اطمینان را کاهش دهید، طول بازه نیز کاهش یافته ولی دقت در برآورد بیشتر میشود. برعکس اگر درصد اطمینان را افزایش دهید، طول بازه گستردهتر شده و دقت کاهش مییابد.
تعادل بین توان آزمون و آزمون تعقیبی
پس آزمونها، یکی از بهترین روشها برای کنترل کلی خطای آزمونهای «مقایسههای چندگانه» (Multiple Comparison) هستند. از طرفی توان آزمونهای آماری نیز یکی از بحثهای مهم در انتخاب بهترین آزمونها است. در اکثر مواقع دوست داریم که آزمونی به کار گرفته شود که بیشترین «توان آزمون» (Power of test) را داشته باشد.
متاسفانه هنگامی که از پس آزمون یا آزمون تعقیبی برای کنترل خطای نوع اول، استفاده میکنیم، خطای نوع دوم افزایش یافته در نتیجه توان آزمون کاهش خواهد یافت. در حقیقت آزمونهای تعقیبی با کاهش توان آزمون، خطای نوع اول را کنترل میکنند. به همین جهت بهتر است بین توان آزمون و خطای آزمون، یک تعادل برقرار کرده و آزمونی را انتخاب کنیم که برای هر دو نوع خطا، کمترین میزان را داشته باشد.
فرض کنید در یک آزمون مقایسههای دوتایی، بخواهیم خطای نوع اول یا سطح معنیداری را برای هر یک از آزمونها کنترل کنیم. «پس آزمون» به کار رفته برای انجام این کار، میزان خطای نوع اول را برای هر یک از آزمونهای مقایسهای مجزا (غیر همزمان) کمتر از خطای معمول میکند.
برای مثال، برای رسیدن به سطح آزمون خانوادگی آزمونها در سطح ۵٪، هر یک از تک آزمونها باید در سطح کمتر از ۵٪ صورت گیرند. از طرفی هر گاه تعداد آزمونهای مقایسهای، افزایش یابد، باید از سطح آزمون نیز کاسته شود.
برای مثال، اگر شش مقایسه دو تایی در یک آزمون به کار رود، در روش توکی برای هر یک از آزمونهای نمونههای مستقل، تقریبا سطح معنیداری را باید برابر با ۰٫۰086 در نظر گرفت. در این صورت اگر را میزان خطای خانواده آزمونها و را سطح یا اندازه هر یک از آزمونها در نظر بگیریم، خواهیم داشت:
به این ترتیب با جایگذاری مقدار ۰٫۰۵ برای ، مقدار حاصل میشود.
همانطور که دیده میشود، سطح آزمونهای تکی برای چنین حالتی بسیار کمتر از سطح آزمون عادی در تحلیل یا آزمونهای آماری در تحلیل واریانس (ANOVA) است.
این موضوع با توجه به توازنی که بین سطح آزمون و احتمال خطای نوع دوم برقرار است، باعث کاهش توان آزمون میگردد. میدانیم که اگر احتمال خطای نوع دوم (احتمال رد کردن فرض مقابل به اشتباه) را با نمایش دهیم، در اندازه نمونه ثابت، کاهش ، باعث افزایش میشود. در این صورت واضح است که توان آزمون در این میان، کاهش مییابد.
نکته: کاهش توان آزمون بیانگر آن است که اگر واقعا بین میانگین جمعیتها اختلاف وجود داشته باشد، به کمک این آزمونها قادر به تشخیص آن نیستیم.
به همین علت گاهی در آزمونهای مربوط به مقایسههای همزمان، سطح آزمون را به جای ۰٫۰۱، همان ۰٫۰۵ در نظر گرفته تا توان آزمون کاهش نیابد.
البته راه دیگر برای افزایش توان آزمون، استفاده از تعداد نمونههای بیشتر در طرح آنالیز واریانس است. با این کار خطای یا سطح آزمون () ثابت مانده ولی خطای نوع دوم کاهشی شده، در نتیجه توان آزمون بیشتر از حالتی است که تعداد نمونهها کم باشند.
یک دیدگاه دیگر برای افزایش توان آزمون، کاهش تعداد مقایسههای دوتایی است. به این ترتیب ایجاد «کنتراست» (Contrasts) یا تقابلها، میتواند توان آزمون را افزایش داده زیرا در مقابل از تعداد مقایسههای دو تایی کاسته شده است.
نکته: به عنوان یک قانون کلی میتوان گفت، هر چه تعداد مقایسههای دوتایی افزایش یابد، توان آزمون در مقابل کاهش مییابد و برعکس، اگر از تعداد مقایسههای دو تایی بکاهیم، توان آزمون را افزایش دادهایم.
کاهش مقایسههای زوجی و موازنه بین خطای نوع اول و توان آزمون
تا اینجا بحث بر سر نحوه اجرای مقایسههای دو تایی و کنترل خطای نوع اول در آزمونهای همزمان و پس آزمون یا آزمون تعقیبی بود. ولی در این قسمت میخواهیم روشی را به کار بگیریم که به کمک آن قادر به کنترل توان پس آزمون یا آزمون تعقیبی باشیم. این کار در این مرحله براساس کاهش تعداد مقایسههای دو تایی صورت میگیرد. در نتیجه فقط مقایسههایی را انجام میدهیم که دارای «تضاد» (Contrast) باشند.
به دلایل مختلف ممکن است طرح تحقیقی شما، فقط به زیرمجموعهای از همه مقایسههای دوتایی ممکن، نیاز داشته باشد. در این بین ممکن است دو علت اصلی برای اجرای طرح «مقایسه تضادها» (Contrast) وجود داشته باشد که در این متن به آنها اشاره خواهیم کرد. در این بین، آزمون مناسب برای اجرای مقایسه تضادها نیز مورد بررسی قرار خواهد گرفت. معمولا چنین آزمونهایی را «آزمونهای طرحریزی شده» (Designed tests) یا «پیش آزمون» (Pre-Test) در مقابل پس آزمون (Post-Hoc) مینامند، زیرا قبل از اجرای آزمون میدانیم، هدف مقایسهای بین گروههایی است که از قبل مشخص شدهاند.
برای مثال ممکن است برای تشخیص اختلاف بین ۳ گروه، فقط به سه یا چهار آزمون متضاد احتیاج باشد در حالیکه در «روش توکی» همه ۶ حالت ترکیب گروهها مورد آزمون قرار میگرفت.
نکته: در پس آزمون، بعد از رد شدن فرض صفر به دنباله پیدا کردن زوجهایی هستیم که باعث رد فرض صفر شدهاند. ولی در «پیش آزمون»، قبل از اجرای آزمون یک طرح آزمایش، تهیه شده و گروههایی مقایسهای در بین همه گروهها مشخص شدهاند. معمولا طرح پیش آزمون براساس گروههای انتخابی به جای انتخاب تصادفی، صورت میگیرد.
نکته: استفاده از یک طرح آزمایش پیشآزمون، باعث کاهش تعداد آزمونها شده و به نوعی غربال آزمونها اتفاق میافتد. بنابراین قبل از اجرای آزمون آماری و حتی جمعآوری دادهها، باید استراتژی و هدف از اجرای آزمون را مشخص کرده و براساس آن دست به اجرای «پس آزمون» یا «پیش آزمون» زد.
استفاده از روش دانت برای مقایسه گروههای درمانی با گروه کنترل
اگر مطالعه شما دارای گروه کنترل و چندین گروه تیمار است، ممکن است لازم باشد گروههای تیمارها را فقط با گروه کنترل مقایسه کنید. در این صورت بهتر است از «روش دانت» (Dunnett Method) برای انجام این مقایسهها، بهره ببرید. این امر به این معنی است که قبل از اجرای طرح آنالیز واریانس (در راستای طرح تحقیقی)، میدانید کدام گروه (کنترل) را میخواهید با گروههای دیگر (تیمارها) مقایسه کنید. در این صورت نیازی نیست همه تیمارها (ترکیب کنترل و تیمارها) را با یکدیگر مقایسه کنید.
در این بخش از «روش دانت» (Dunnett Method) استفاده خواهیم کرد. البته فرض بر این است که در یک طرح «تحلیل واریانس یک طرفه» (One-way ANOVA) میخواهیم از آزمون دانت کمک بگیریم. البته باز هم مثال اولیه ANOVA را به کار خواهیم گرفت تا درک بیشتری نسبت به مفاهیم به کار رفته در روش دانت بدست آوریم. البته سناریو را کمی تغییر خواهیم داد. فرض کنید در حال حاضر از ماده A استفاده میکنیم. این آزمون را برای مقایسه مواد جایگزین (B ،C و D) با آن انجام دادیم. به این ترتیب ماده A، گروه کنترل خواهد بود، در حالی که سه مورد دیگر این تیمارها هستند. میخواهیم بدانیم که با توجه به گران بودن ماده A، میتوان یکی از مواد دیگر را جایگزین کرد یا خیر.
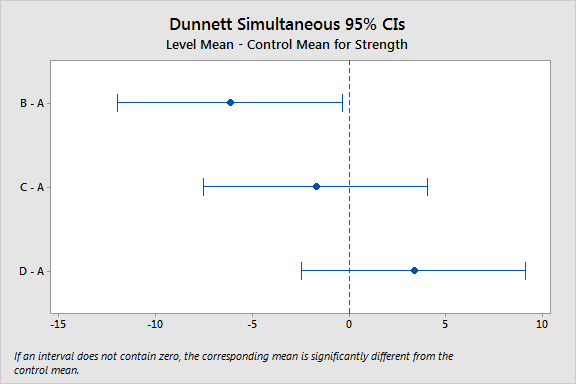
با استفاده از روش Dunnett، مشخص میشود که فقط اختلاف B - A از نظر آماری معنیدار است، زیرا فاصله اطمینان همزمان برای آن شامل صفر نمیشود. البته با توجه به تصویر 6 مشخص است که در «روش توکی»، این مقایسه معنی دار نبود. این موضوع به علت افزایش توان آزمون دانت نسبت به همه مقایسهها در آزمون توکی است. از طرف دیگر، برخلاف روش توکی، روش دانت متوجه نمیشود که اختلاف D - B معنیدار است زیر فقط به اختلاف تیمارها با گروه کنترل یعنی A توجه دارد.
استفاده از Hsu MCB برای یافتن قویترین ماده
اگر هدف مطالعه یا طرح تحقیقی، شناسایی بهترین گروه (یا تیمار) است، ممکن است نیازی به مقایسه همه زوجهای نباشد. «مقایسههای چندگانه بهترین سو» (Hsu’s Multiple Comparisons to the Best) گروههایی را که بهترین بوده را شناسایی میکند. این امر همچنین گروههایی که تفاوت معنیداری با بهترین گروه دارند را هم معرفی میکند. از طرفی با توجه به روش MCB Hsu قادر هستیم، گروههایی را کشف و مشخص کنیم که اختلاف معنیداری با گروه برتر ندارند.
زمانی از آزمون Hsu's MCB استفاده کنید که یکی از حالتهای زیر رخ داده است:
- از قبل نمیدانید کدام گروه را میخواهید با همه گروههای دیگر مقایسه کنید.
- نیازی نیست گروههایی که بهترین نیستند را با یکدیگر مقایسه کنیم.
- میتوان «بهترین» را به عنوان گروهی با بالاترین میانگین یا کمترین میانگین تعریف کرد.
MCB Hsu هر گروه را با «گروه بهترین میانگین» (بالاترین یا پایینترین) مقایسه میکند. با استفاده از این روش، ممکن است به گروههایی برخورد کنید که نسبت به گروه بهترین، تفاوت معنیداری ندارند. ولی به یاد داشته باشید که گروهی که واقعاً در کل جمعیت بهترین است ممکن است به دلیل خطای نمونهگیری، بهترین میانگین نمونهای را نداشته باشد. گروههایی که تفاوت چندانی با بهترین گروه ندارند، ممکن است به همان اندازه خوب بوده و یا حتی از بهترین گروه نیز برتر باشند ولی به دلیل خطای نمونهگیری، نادیده گرفته شدهاند.
فاصلههای اطمینان همزمان برای MCB Hsu
طبق مثالی که مربوط به «تحلیل واریانس یک طرفه» (One-way ANOVA) ارائه کردیم، این بار میخواهیم از موادی استفاده کنیم که قویترین یا بیشترین میزان مقاومت را نسبت به فشار عمودی دارند. در نتیجه، اگر از روش MCB Hsu کمک بگیرم، بالاترین یا بیشترین مقدار میانگین را به عنوان بهترین ماده انتخاب خواهیم کرد. به یاد دارید که در اینجا بزرگی و کوچکی اعداد مهم نیستند بلکه معنیداری آماری اختلاف بین گروهها، بزرگتری یا کوچکتری را نشان میدهد. از این جهت به همه مقایسههای دوتایی احتیاجی نداریم و فقط قرار است بزرگترین میانگین را نسبت به بقیه، مشخص و مقایسه کنیم.
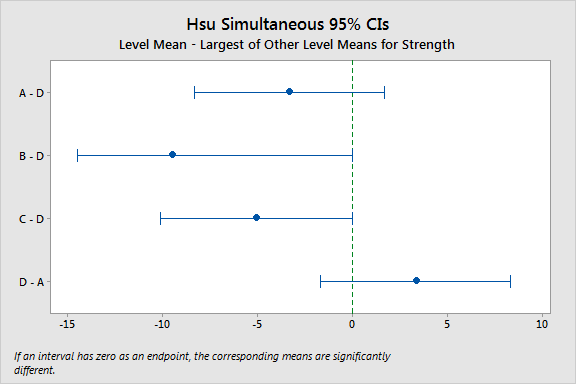
واضح است که طبق نمودار ترسیم شده در تصویر 7، گروه D بهترین گروه است، زیرا بالاترین میانگین را دارد (41٫۰۷). به این ترتیب یک گروه را با بقیه گروهها در روش MCB Hsu مقایسه کرده و بزرگترین اختلاف را مبنای انتخاب گروه برتر در نظر میگیریم.
در روش آزمون MCB Hsu، گروه مورد نظر، زمانی نسبت به بقیه گروهها برتر است که یکی از کرانهای فاصله اطمینان برای اختلاف میانگینها، برابر با صفر باشد. این موضوع را از طریق نمودار ترسیمی نیز میتوان مشاهده کرد. به این ترتیب مشخص میشود که ماده D با اختلاف معنیداری بهتر از مواد B و C است. با این حال، فاصله اطمینان برای مقایسه A-D نیز حاوی صفر است، که نشان میدهد ماده A از لحاظ ظاهری تفاوت چندانی با بهترین گزینه (یعنی ماده D) ندارد. این نتایج حاصل به کارگیری پس آزمون یا آزمون تعقیبی است.
خلاصه و جمعبندی
همانطور که مشخص شد، استراتژی طرح تحقیق در «تحلیل واریانس» (ANOVA) تعیین میکند که آیا میانگینهای گروهها، به طور کلی متفاوت هستند یا خیر. متاسفانه تحلیل واریانس ابزار مناسبی برای تشخیص گروه یا گروههایی نیست که باعث تفاوت شدهاند. اگر نتایج حاصل از «جدول تحلیل واریانس» (ANOVA Table)، شواهدی بر نابرابری در بین گروهها باشد، از یک پس آزمون یا آزمون تعقیبی استفاده کرده تا میانگین اختلاف بین زوج گروه را بررسی و مشخص کنیم که علت رد فرض صفر در تحلیل واریانس کدام زوج (یا زوجها) است. در این بین اگر نیازی نیست که همه مقایسههای زوجی صورت گیرد، بهتر است از مقایسههای تضادها (Contrasts) استفاده کرده تا تعداد مقایسههای زوجی کاهش یافته و توان آزمونهای افزایش یابد.
آنچه در این نوشتار خواندید، خلاصهای در مورد پس آزمون یا آزمون تعقیبی در تحلیل واریانس بود که البته به شیوههای مختلف اجرای آن نیز اشاره شد. علت به کارگیری این روشها به جای آزمونهای مقایسهای دو تایی نیز در متن مورد بحث قرار گرفت. هر چند تکنیکهای خاص و مختلفی برای اجرای پس آزمونها وجود دارد ولی شرایط به کارگیری هر یک از آنها متفاوت بوده و با توجه به آنها باید نسبت به انتخاب پس آزمون یا آزمون تعقیبی مناسب اقدام کرد تا نتایج حاصل از آزمونهای آماری قابل اعتماد باشند.













با سلام و تشکر بابت مطالب بسیار خوب و کاربردی که زحمت میکشید و ارائه میدهید
آیا اگر از آزمون های ناپارامتری مثل کروسکال والیس هم تفاوت را نتیجه بگیریم باز هم میشه از آزمون های تعقیبی استفاده کرد ؟
اگر نمیشه از چه آزمونی میشه بجای آزمون تعقیبی استفاده کرد؟
ممنون میشم راهنمایی بفرمایید
سلام. من ANOVA گرفته ام و معنی دار شده است. اما آزمون تعقیبی که می گیرم محل تفاوت را نشان نمی دهد. یعنی معنی دار نمی شود. یک بار Dunnet t3 گرفتم و یک بار Games-Howell گرفتم. هیچ کدام معنی دار نمی شود. اشکال کار کجاست؟؟؟ ممنون می شوم راهنمایی بفرمایید
سلام ، tokey و LSD رو بگیر
سلام اگر مطلب آموزشی قرار می دهید لطفا رفرنس رو هم قرار بدهید.
با سلام؛
منابع تمامی مطالب مجله فرادرس در انتهای مطلب و پیش از نام نویسنده درج شدهاند.
با تشکر از همراهی شما با مجله فرادرس
سلام و سپاس از مطالب عالی شما
آیا میشود تفاوت میانگین دو گروه در پیش آزمون با سطح معنی داری 0.05 ، پس آزمون 0.01 و پیگیری 0.05 باشد، یعنی سطح معنی داری متفاوت باشد یا باید همه مراحل با سطح معنی داری مساوی تفسیر شود؟