حل معادله درجه ۳ – به زبان ساده
پیشتر در وبلاگ فرادرس نحوه حل معادلات درجه دوم را بیان کردیم. در این مطلب قصد داریم تا یک قدم به جلوتر رفته و روش حل معادله درجه ۳ را شرح دهیم.


مقدمه
در مطلب معادلات درجه دوم، شکل عمومی یک معادله درجه ۲ و پاسخ مرتبط با آن را بهصورت زیر بیان کردیم:
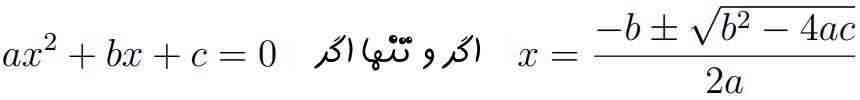
عبارت را دلتا () نامیده و پاسخهای معادله متناسب با شرایط دلتا بهصورت زیر پیدا شدند:
- اگر باشد، معادله درجه ۲ دارای دو پاسخ حقیقی است.
- اگر باشد، معادله دارای دو پاسخ مشابه (یا اصطلاحا ریشه مضاعف) است.
- اگر باشد، معادله در اعداد حقیقی پاسخی نخواهد داشت.
مشابه با معادله درجه ۲، به منظور حل معادله درجه ۳ نیز میتوان پاسخی بهصورت عمومی اما پیچیدهتر بدست آورد. جالب است بدانید برای معادلات درجه ۴ و بالاتر نیز میتوان روابط کلی ارائه داد، اما روابط مذکور بسیار پیچیده خواهند بود.
معادله درجه ۳
جهت حل معادله درجه ۳ در ابتدا بایستی با قالب کلی این نوع از معادلات آشنا باشید. شکل عمومی یک معادله درجه ۳ بهصورت زیر است.
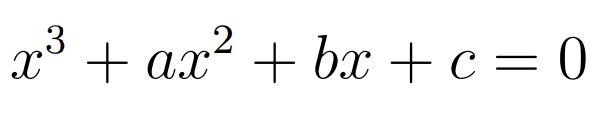
در برخی از موارد ممکن است شکل اولیهای از معادله درجه ۳ که با آن روبرو هستید، بهصورت بالا نباشد. در این شرایط میتوانید با ضرب و تقسیم کردن ضرایب، معادله را بهشکل عمومی در آورید. برای نمونه معادله زیر را در نظر بگیرید.

همانطور که میبینید در معادلهی بالا ضریب x3 برابر با ۱ نیست؛ بنابراین شکل معادله برای حل، استاندارد نبوده و بایستی آن را بهصورت استاندارد بیان کرد. در نتیجه تمامی ضرایب را به ضریب x3 تقسیم کرده و رابطه بالا را بهصورت زیر مینویسیم.
با مقایسه معادله فوق با رابطه ۱ میبینیم که شکل معادله بهصورت استاندارد در آمده است. در نتیجه ضرایب a,b,c برابرند با:
حال با یادگیری شکل استاندارد یک معادله، زمان آن فرا رسیده تا مراحل حل معادله درجه ۳ را توضیح دهیم.
قدم اول
با توجه به ثابتهای a,b,c، ضرایبی تحت عنوان p و q را بهصورت زیر بدست آورید.
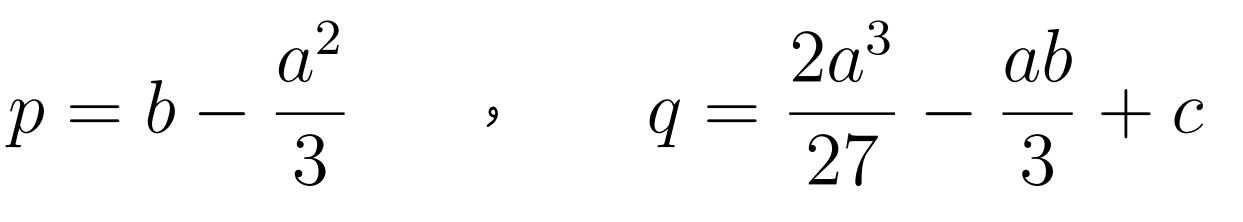
پس از محاسبهی p و q مقدار مشخصه (همان دلتای معادله درجه ۳) را با استفاده از فرمول زیر بدست آورید.
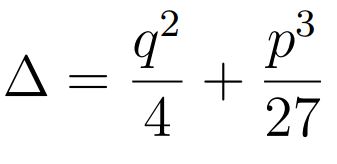
قدم دوم
پس از محاسبهی Δ، سه حالت برای آن وجود خواهد داشت. در هریک از این حالات پاسخ x به شکلی متفاوت خواهد بود که در زیر بیان شده است.
حالت اول:
اگر باشد، تنها یک پاسخ حقیقی برای معادله وجود خواهد داشت که مقدار آن برابر است با:
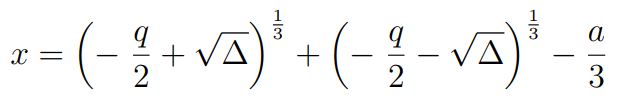
حالت دوم:
در این حالت معادله دارای سه ریشه خواهد بود. اما دو ریشه با هم برابر هستند (به عبارت دیگر یک ریشه مضاعف در این حالت وجود دارد). مقدار این سه ریشه برابر است با:

حالت سوم:
در این حالت، معادلهی درجه ۳ دارای سه پاسخ متفاوت خواهد بود که در ادامه ذکر شده است.
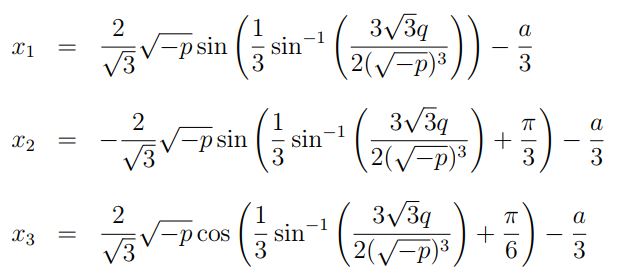
نهایتا با استفاده از دو قدم بیان شده در بالا به یکی از حالات دلتا رسیده و میتوانید پاسخ معادله را بیابید. در ادامه جهت تسلط به روش مذکور، مثالهایی ارائه شده است.
مثال ۱
تمامی پاسخهای حقیقی معادله زیر را بیابید.
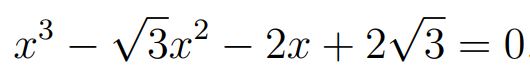
پاسخ: با توجه به معادلهی فوق، مقادیر a,b,c برابرند با:
با مشخص کردن ضرایب a,b,c مقادیر p و q برابرند با:
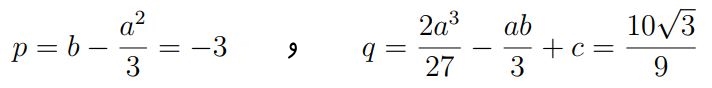
بنابراین دلتا (Δ) برابر است با:
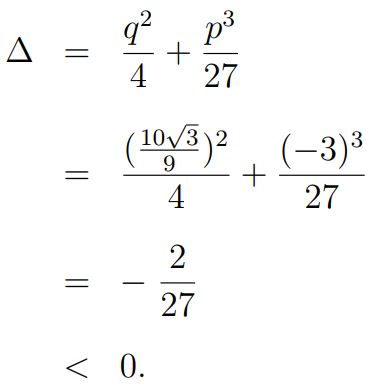
مقدار دلتای بدست آمده منفی است؛ در نتیجه معادله دارای سه پاسخ متفاوت خواهد بود. این پاسخها برابرند با:
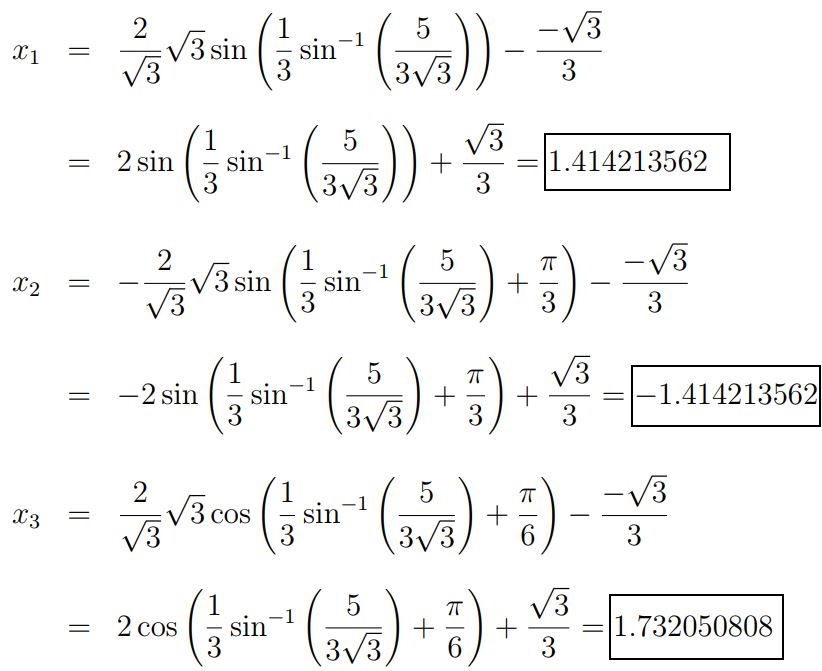
که به ترتیب، همان ، و هستند. ظاهر روابط بالا پیچیده بهنظر میرسد، اما این روابط تنها محاسبه سینوس و کسینوس یک زاویه هستند!

مثال ۲
تمامی پاسخهای حقیقی معادلهی زیر را بیابید.
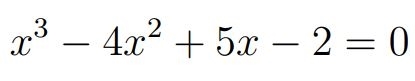
پاسخ: با توجه به معادلهی فوق a=-4,b=5,c=-2 هستند. در نتیجه مقادیر p و q برابرند با:
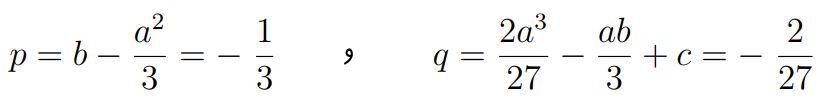
در نتیجه مقدار Δ نیز برابر است با:
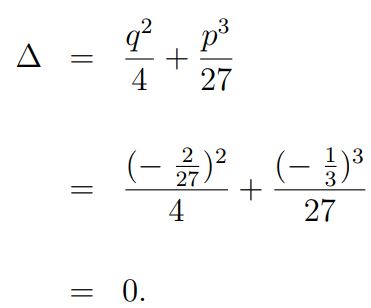
مقدار Δ=۰ است؛ بنابراین یکی از پاسخهای معادله تکرار خواهد شد. این پاسخها برابرند با:
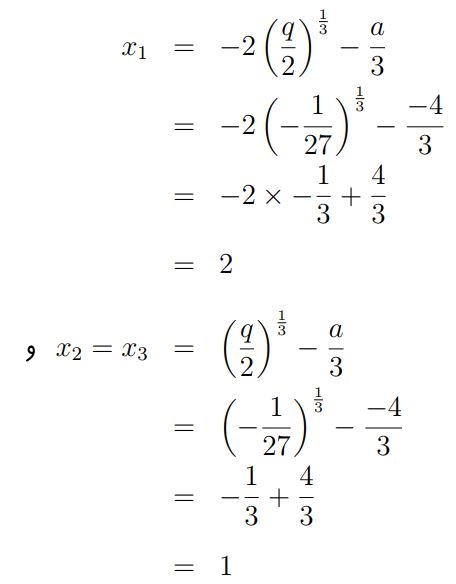
پاسخهای مختلف x نشان میدهد که برخلاف معادله درجه ۲، معادله درجه ۳ همواره دارای حداقل یک پاسخ حقیقی است. همانطور که پیشتر نیز بیان شد، ریشههای یک معادله در حقیقت محل برخورد نمودار با محور x هستند. در مواردی که یک نمودار به محور x مماس شود، ریشه تکرار میشود. در شکل زیر سه حالت متفاوتی که در آن معادلهای درجه ۳ محور xها را قطع کرده، نشان داده شده است.
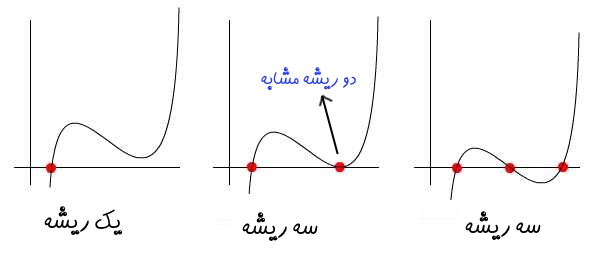
نمودار سمت راست متناسب با مثال ۱ است؛ چراکه نمودارِ نشان داده شده در سه نقطه متفاوت محور x را قطع میکند. در نتیجه نمودار سمت راست نشان دهندهی معادلهای است که دارای سه پاسخ متفاوت است. نمودار وسط نیز مشابه با مثال ۲ است؛ چرا که محور xها را در دو نقطه قطع کرده و در یکی از نقاط نیز به نمودار مماس شده است. بنابراین نمودار وسط معادلهای را نشان میدهد که دارای دو ریشه مشابه و یک ریشه متفاوت است.
آزمون حل معادله درجه ۳
۱. فرم استاندارد معادله درجه ۳ چگونه نوشته میشود و هر یک از ضرایب a، b و c چه نقشی دارند؟
در فرم استاندارد، ضریب x^3 هر مقداری میتواند باشد و a مربوط به x^2، b به x و c عدد ثابت است.
ضرایب a، b، c فقط در معادلات درجه دو استفاده میشوند و در درجه سه کاربرد ندارند.
در فرم استاندارد، ضریب x^3 برابر ۱ است و ضرایب a، b، c به ترتیب جلوی x^2، x و عدد ثابت قرار میگیرند.
ضریب a همیشه باید صفر باشد تا معادله ساده شود و b و c جلوی x و عدد ثابت باشند.
در فرم استاندارد معادله درجه ۳، ضریب x^3 باید ۱ باشد و ضرایب a، b و c به ترتیب جلوی x^2، x و عدد ثابت قرار میگیرند تا معادله برای حل ساده شود. بیان اینکه ضریب a باید همیشه صفر باشد نادرست است، چراکه این ضریب نقش مهمی در بخش x^2 دارد. اینکه ضریب x^3 هر مقداری میتواند باشد درست نیست، چون با تقسیم بر ضریب آن باید به فرم استاندارد برسیم. همچنین ضرایب a، b و c مختص معادلات درجه ۳ نیز هستند و ادعای کاربرد تنها در درجه دو نادرست است.
۲. وقتی برای یک معادله درجه ۳ مقدار دلتا منفی باشد، وضعیت ریشههای حقیقی آن چگونه است و دلیل این حالت چیست؟
دو ریشه حقیقی برابر و یک ریشه مختلط داریم، چون دلتا منفی تقسیمبندی ریشهها را محدود میکند.
فقط یک ریشه حقیقی داریم و دو ریشه مختلط، چون دلتا منفی است.
هیچ ریشه حقیقی وجود ندارد، چون دلتا منفی باعث حذف پاسخهای حقیقی میشود.
سه ریشه حقیقی مختلف خواهیم داشت، چون دلتا منفی است و فرمولهای مربوط به این حالت، امکان وجود سه جواب مجزا را فراهم میکند.
وقتی مقدار دلتا (delta) برای معادله درجه ۳ منفی باشد، سه ریشه حقیقی مختلف بهدست میآیند. این نتیجه به خاطر ویژگی روابط مربوط به دلتا منفی در معادلات درجه ۳ است که امکان وجود سه جواب مستقل را ایجاد میکند. گزینههای «هیچ ریشه حقیقی وجود ندارد» و «دو ریشه حقیقی برابر و یک ریشه مختلط» نادرست هستند، زیرا این حالات در شرایط دلتا صفر یا سایر شرایط رخ میدهد. همچنین عبارت «فقط یک ریشه حقیقی و دو ریشه مختلط» مربوط به حالت دلتا مثبت است، نه دلتا منفی.













مجموع و تفاضل ریشه های معادله درجه سوم بر چه اساسی است؟
با سلام خدمت شما همراه گرامی؛
مجموع ریشهها در معادله درجه سوم (ax³ + bx² + cx + d = 0) برابر میشود با b/a- اما یافتن تفاضل ریشهها محاسبه پیچیدهتری دارد و به طور مستقیم فرمول سادهای ندارد. میتوان تفاضل را با کم کردن بزرگترین ریشه از کوچکترین ریشه به دست آورد. این تفاضل، به طور کلی به ریشهها و ضرایب معادله وابسته است. روشهای مختلفی برای یافتن ریشهها (مانند روش کارتزیا) وجود دارد که به محاسبه نیز تفاضل کمک میکند. به طور خلاصه، مجموع ریشه ها فرمول سادهای دارد، اما تفاضل نیازمند محاسبات پیچیدهتری است.
از بازخورد و همراهی شما با مجله فرادرس سپاسگزاریم.
لذت بردم. مرسی
سلام میشه حل معادله درجه 3 را به روش هورنر هم بزارید
اون a رو چگونه بدست بیاریم
با زبان های برنامه نویسی من انجام دادم جواب رو کمپلکس نشان میده
درحالی که دلتا دارای ۳ ریشه متفاوت است عدد پی را چند باید بگیریم ؟
روشی آسون تر نیست که وقت کم تری بگیره؟
می توانی از نکته ` a+b+c+d=0 ` » X=1 استفاده کنی بعد برای پیدا کردن ریشه های دیگر معادله است را با تجزیه به `x-1` پیدا کنی
روش عددی هورنر رو یاد بگیر جالبه.
در هر حال حل معادلات درجه ۳ شدنی اما طولانیه.
ریشه های موهومی رو چجوری بدست بیاریم؟
خیلی خوب بود
ممنونم از شما❤
سلام.
برای این کار میتوانید چندجملهای را بر (x−a) تقسیم کنید و به یک معادله درجه دوم برسید (a ریشه حقیقی معادله درجه سوم است). سپس ریشههای معادله درجه دوم را محاسبه کنید.
موفق باشید.
اثبات هم بزارید
اثبات پارامتری رو میخواستم لطفا.
روش دلتا بیشتر شبیه بازیه عموما در حل معادله استفاده نمیشه ، احیانا با نرم افزارهای ریاضی بدست آوردن. احتمالا بتونی با متلب بدست بیاری.
دمتون گرم
اگر
p=-2243
و q=-235
دلتا کوچیکتر از صفر
معادله ایی با این مشخصات میشه برام حل کنید؟
متشکر
نیما
سلام
من روش گفته شده را در معادله s^3+s^2-s+2 قرار دادم جواب معادله صحیح نیست.
سلام.
همانگونه که در متن نیز اشاره شده است، این روش برای یافتن ریشههای «حقیقی» معادله درجه سه به کار میرود. معادله s3+s2−s+2=0 ریشه مختلط دارد.
از همراهی شما با مجله فرادرس سپاسگزاریم.