معادلات دیفرانسیل مرتبه دوم ناهمگن — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

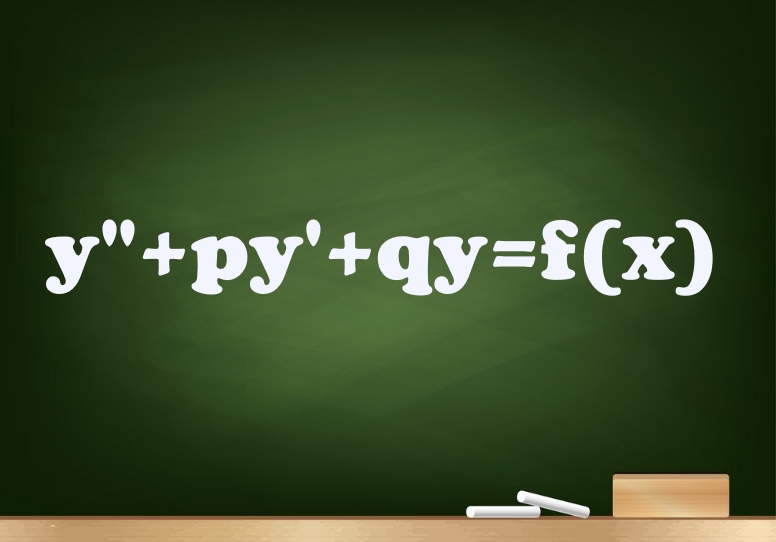
در راستای ارائه مفاهیم مرتبط با معادلات دیفرانسیل، در این مطلب می‌خواهیم تا نحوه حل معادلات دیفرانسیل مرتبه دوم ناهمگن را توضیح دهیم. بدین منظور پیشنهاد می‌شود در ابتدا مطلب معادلات دیفرانسیل را مطالعه فرمایید.

شکل معادله دیفرانسیل ناهمگن

شکل عمومی یک معادله دیفرانسیل ناهمگنِ مرتبه دو به صورت زیر است.

$$ \large { y ^ { \prime \prime } + p y ^ { \prime } + q y } = { f\left ( x \right ) } $$

فیلم آموزش معادلات دیفرانسیل به همراه حل سوالات آزمون کارشناسی ارشد

اینجا کلیک کنید

در رابطه فوق مقادیر $$p$$ و $$q$$ اعداد ثابتی هستند. هر دوی این اعداد می‌توانند ثابت یا مختلط باشند. معادله همگن مرتبط را نیز می‌توان به صورت زیر بیان کرد:

$$\large { y ^ { \prime \prime } + p y ^ {\prime} + q y } = { 0 } $$

قضیه: پاسخ عمومی معادله ناهمگن، برابر با حاصل جمع پاسخ‌ عمومی معادله همگن و پاسخ خصوصی معادله ناهمگن است. توجه داشته باشید که در مسائل، پاسخ خصوصی را با $$ { y _ 1 } \left ( x \right ) $$ و پاسخ عمومی را با $$ { y _ 0 } \left ( x \right ) $$ نشان می‌دهیم. با این فرض پاسخ عمومی معادله ناهمگن برابر است با:

$$ \large { y \left ( x \right ) } = { { y _ 0 } \left ( x \right ) + { y _1 } \left ( x \right ) } $$

در ادامه دو روش به منظور بدست آوردن پاسخ عمومی معادله ذکر شده است.

روش تغییر ثابت‌ها

فرض کنید پاسخ عمومی یک معادله دیفرانسیل همگن برابر با $$y_0$$ باشد. هم‌چنین در نظر بگیرید که شکل کلی این پاسخ به صورت زیر بدست آمده است.

$$ \large { { y _ 0 } \left ( x \right ) } = { { C _1 } { Y _ 1 } \left ( x \right ) } + { { C _ 2 }{ Y _ 2 } \left ( x \right ) } $$

حال می‌توان پاسخ عمومی معادله ناهمگن را با ضرایب متغیر در نظر گرفت. در حقیقت در این حالت پاسخ عمومی معادله ناهمگن برابر است با:

$$ \large { y = { C _ 1 } \left ( x \right ) {Y _ 1 } \left ( x \right ) } + { { C _ 2 } \left ( x \right ) { Y _ 2 } \left ( x \right ) } $$

پاسخ عمومی فرض شده باید در معادله همگن و معادله ناهمگن صدق کند. بنابراین دو معادله مورد نیاز به منظور یافتن ثابت‌ها به صورت زیر خواهند بود.

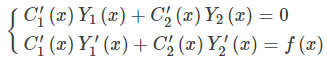
با حل کردن دو معادله فوق، ضرایب $$C_1(x)$$ و $$C_2(x)$$ بدست آمده و پاسخ عمومی معادله ناهمگن بدست می‌آید.

روش ضرایب نامعین

معمولا در سمت راست معادلات ناهمگن، تابع $$f(x)$$، ترمی چند جمله‌ای، نمایی یا مثلثاتی یا ترکیبی از این توابع است.

فیلم آموزش معادلات دیفرانسیل با میپل Maple

اینجا کلیک کنید

در مواردی که با چنین توابعی مواجه‌اید، بهتر آن است که از روش ضرایب نامعین استفاده شود. در ادامه نمونه‌هایی از این توابع $$f(x)$$ شده‌اند.

• $$ \large f \left ( x \right ) = { P _ n } \left( x \right) { e ^ { \alpha x } } $$
• $$\large f \left ( x \right ) = \left [ { { P_ n } \left ( x \right ) \cos \left ( { \beta x } \right ) } \right. \left.{+{ Q _ m } \left ( x \right ) \sin \left( {\beta x} \right)} \right]{ e ^ { \alpha x } } $$

در روابط فوق، $$P_n(x)$$ و $$Q_m(x)$$، چند‌جمله‌‌ای‌هایی از درجه $$n$$ و $$m$$ هستند. در هر دو حالت، پاسخ خصوصی فرض شده باید ساختاری مشابه با $$f(x)$$ داشته باشد.

در حالت اول اگر توان $$\alpha$$ برابر با ریشه معادله مشخصه باشد، باید ترم $$x^s$$ را نیز در پاسخ خصوصی در نظر گرفت. منظور از $$s$$، توان $$\alpha$$ در معادله مشخصه است. در مثال‌هایی که در انتهای این مطلب ارائه شده، این روش را به طور کامل توضیح خواهیم داد.

حالت دوم زمانی است که ریشه معادله مشخصه، عدد مختلطِ $$ \alpha + \beta i $$ باشد. در این حالت نیز پاسخ خصوصی فرض شده باید در متغیر‌های $$x$$ ضرب شود. ضرایب ثابت را نیز می‌توان با قرار دادن پاسخ فرض شده در معادله اصلی بدست آورد.

روش برهم‌نهی

فرض کنید سمت راست معادله ناهمگن یا همان $$f(x)$$، جمع توابعی به صورت زیر باشد.

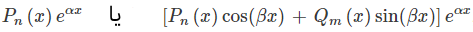
مثال ۱

پاسخ عمومی معادله دیفرانسیل زیر را با استفاده روش تغییر ثابت‌ها بیابید.

$$ \large y ^ { \prime \prime } + y = \sin \left ( { 2 x } \right) $$

همان‌طور که در بالا نیز بیان شد، در ابتدا باید پاسخ معادله همگن را یافت. معادله همگن مرتبط به صورت زیر است.

$$ \large y ^ { \prime \prime } + y = 0 $$

معادله مشخصه و ریشه‌های آن برابرند با:

$$ \large { { k ^ 2 } + 1 = 0 \; \; } \Rightarrow { { k ^ 2 } = – 1 \; \; } \Rightarrow { { k _ { 1 , 2 } } = \pm i } $$

بنابراین پاسخ عمومی معادله همگن برابر است با:

$$ \large { { y _ 0 } \left ( x \right ) } = { { C _ 1 } \cos x } + { { C _ 2 } \sin x } $$

با توجه به شکل پاسخ عمومی معادله همگن، پاسخ عمومی معادله ناهمگن را می‌توان به صورت زیر در نظر گرفت.

$$ \large { y \left ( x \right ) } = { { C_ 1 } \left ( x \right ) \cos x }+{ { C _ 2 } \left( x \right)\sin x } $$

با قرار دادن پاسخ در نظر گرفته شده در دو معادله همگن و ناهمگن، سیستم معادلات به صورت زیر بدست خواهد آمد.

$$\large \left\{ \begin{array}{l} { { C ^ { \prime} _1}\left( x \right)\cos x} + { { C ^{\prime} _2}\left( x \right)\sin x} = 0 \\ { C ^ { \prime } _1 } \left ( x \right ) { \left( {\cos x} \right)^\prime } + {C ^{\prime} _ 2 } \left( x \right){\left( {\sin x} \right ) ^ \prime } = {\sin 2 x } \end{array} \right.$$

دو معادله فوق را می‌توان به صورت زیر بازنویسی کرد.

$$ \large \left\{ \begin{array}{l} { { C ^ { \prime} _ 1 } \left( x \right)\cos x} + {{C ^{\prime}_2}\left( x \right)\sin x} = 0 \\ { { C ^{\prime} _1 } \left ( x \right ) \left ( { – \sin x} \right)} + {{C ^{\prime} _2}\left( x \right) \cos x } = { \sin 2 x } \end {array} \right.$$

بنابراین می‌توان مشتقِ $$ { C ^ {\prime} _ 1 } \left ( x \right ) $$ را به صورت زیر بیان کرد:

$$\large { C ^ { \prime } _ 1 } \left ( x \right ) = – { C ^ { \prime } _ 2 } \left ( x \right ) \frac { { \sin x } } { { \cos x } } $$

با قرار دادن $$ { C ^ {\prime} _ 1 } \left ( x \right ) $$ در معادله دوم، $$ { C ^ {\prime} _ 2 } \left ( x \right ) $$ نیز به صورت زیر بدست خواهد آمد.

$$ \large \begin {align*} { \left ( { – { C ^ { \prime } _ 2 } \left( x \right)\frac { { \sin x } } { { \cos x} } } \right ) \left ( { – \sin x } \right ) } + { { C ^ { \prime } _ 2 } \left ( x \right ) \cos x = \sin 2 x \;\;} & \Rightarrow { { { C ^{\prime} _ 2 }\left( x \right)\left( { \frac { { { { \sin } ^ 2 } x } } { { \cos x } } + \cos x } \right ) } = { \sin 2 x \;\; } } \\ & \Rightarrow { { { C ^ { \prime } _ 2 } \left( x \right)\frac { { { { \sin } ^ 2 } x + {{\cos } ^ 2 } x } } { { \cos x} } }={ \sin 2 x }} \\ & \Rightarrow { {C ^ { \prime } _ 2 } \left( x \right ) \frac { 1 } { { \cos x}} = \sin 2 x} \\ & \Rightarrow { { C ^ { \prime } _ 2 } \left ( x \right ) = \sin 2 x \cos x } \end {align*} $$

بنابراین $$ { C ^ {\prime} _ 1 } \left ( x \right ) $$ نیز برابر با عبارت زیر بدست می‌آید.

$$ \large { { C ^ { \prime } _ 1 } \left ( x \right ) } = { – \sin 2 x \cos x \cdot \frac { { \sin x } } { { \cos x } } } = { – \sin 2 x \sin x } $$

با انتگرال‌گیری از عبارت فوق، توابع $$C_1(x)$$ و $$C_2(x)$$ برابر با عبارات زیر بدست می‌آیند.

$$ \large \begin {align*} { { C _ 1 } \left( x \right) } & = { \int {\left( { – \sin 2x\sin x } \right ) d x } } \\ & = { – 2 \int { { { \sin } ^ 2 } x \cos x d x } } \\ & = { – 2\int { { { \sin } ^ 2 } x d \left( { \sin x } \right)} } \\ & = { – 2 \cdot \frac { { { { \sin } ^ 3 } x } } { 3 } + { A _ 1 } } = { – \frac { 2 } { 3 }{\sin ^ 3 } x + { A _ 1 } } \end {align*} $$

$$ \large \begin {align*} { C _ 2 } \left ( x \right) & = { \int {\left( {\sin 2x\cos x} \right)dx} } \\ & = {2\int {\sin x\,{{\cos }^2}xdx} } \\ & = { – 2\int { { \cos^2 } x d \left( {\cos x} \right)} } \\ & = { – 2 \cdot \frac{{{\cos^3}x}}{3} + {A_2} } = { – \frac{2}{3}{\cos^3}x + {A_2} } \end {align*} $$

در رابطه فوق $$A_1$$ و $$A_2$$، ثابت‌های انتگرال هستند. با بدست آمدن ضرایب، پاسخ عمومی معادله ناهمگن نیز برابر با عبارت زیر بدست می‌آید.

$$ \large \begin {align*} y \left( x \right) & = { {C_1}\left( x \right)\cos x + {C_2}\left( x \right)\sin x } \\ & = {{\left( { – \frac{2}{3}{\sin^3}x + {A_1}} \right)\cos x }}+{{ \left( { – \frac { 2 } { 3 } { \cos^3}x + {A_2}} \right ) \sin x } } \\ & = {{{A_1}\cos x + { A _ 2 } \sin x } - { \frac{2}{3}{\sin ^3}x\cos x }}-{{ \frac{2}{3}{\cos^3}x\sin x }} \\ & = { { { A _ 1 } \cos x + {A_2}\sin x }}-{{ \frac{2}{3}\sin x\cos x\left( {\underbrace {{{\sin }^2}x + {{\cos }^2}x}_1} \right) } } \\ & = {{{A_1}\cos x + {A_2}\sin x }-{ \frac{1}{3} \cdot 2\sin x\cos x } } \\ & = {{{A_1}\cos x + {A_2}\sin x }-{ \frac { 1 } { 3 } \sin 2 x } } \end {align*} $$

مثال ۲

پاسخ عمومی معادله دیفرانسیل ناهمگن زیر را بیابید.

$$\large y ^ { \prime \prime } + y ^ { \prime } – 6 y = 36 x $$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد

اینجا کلیک کنید

در این مثال از روش ضرایب نامعین استفاده خواهیم کرد. همان‌طور که از معادله فوق نیز معلوم است، سمت راست معادله در فرمت $$ f \left( x \right ) = a x + b $$ قرار دارد. بنابراین شکل کلی پاسخ خصوصی معادله ناهمگن را می‌توان به صورت زیر در نظر گرفت.

$$ \large { y _ 1 } = A x + B $$

در نتیجه مشتق اول و دوم پاسخ در نظر گرفته شده برابرند با:

$$ \large { y ^{ \prime } _ 1 } = A \;\; , \;\; { y ^ { \prime \prime } _ 1 } = 0 $$

با قرار دادن مشتقات بدست آمده در معادله اصلی، رابطه مربوط به محاسبه ضرایب به شکل زیر بدست می‌آید.

$$ { 0 + A – 6 \left ( { A x + B } \right ) = 36 x \; \; } \Rightarrow
{ A – 6 A x – 6 B = 36x } $$

معادله آخر به ازای تمامی مقادیر $$x$$ صادق است. از این رو جملات حاوی $$x$$ در دو سمت معادله باید با هم برابر باشند. در نتیجه دو معادله زیر به منظور محاسبه ضرایب، بدست می‌آید.

$$\large \left \{ \begin{array} { l } – 6 A = 36 \\ A – 6 B = 0\end{array} \right. $$

از دو معادله فوق، مقادیر $$A=-6$$ و $$B=-1$$ بدست می‌آیند. بنابراین پاسخ خصوصی نیز برابر است با:

$$\large { y _ 1 } = – 6 x – 1 $$

در بالا پاسخ خصوصی بدست آمد. حال زمان آن رسیده تا پاسخ عمومی را محاسبه کنیم. معادله مشخصه و ریشه‌های آن برابرند با:

$$\large \begin{gather*} { { k ^ 2 } + k – 6 = 0,\;\;} \\~\\ \Rightarrow
{D = 1 – 4 \cdot \left( { – 6} \right) = 25 \;\;} \\~\\ \Rightarrow
{ { k _ { 1, 2 } } = \frac{{ – 1 \pm \sqrt {25} } } { 2 } }={ \frac{{ – 1 \pm 5}}{2} }={ – 3 , 2 } \end{gather*} $$

نهایتا پاسخ عمومی معادله همگن به صورت زیر بدست می‌آید.

$$\large { { y _ 0 } \left ( x \right ) } = { { C _ 1 } { e ^ { – 3 x } } + { C _ 2 }{ e ^{ 2 x } } } $$

با بدست آمدن این پاسخ‌ها، پاسخ عمومی معادله ناهمگن برابر خواهد بود با:

$$\large {y = { y _0 } + { y _ 1 } } = { {C _ 1 } { e ^ { – 3 x } } + { C _ 2 } {e ^ { 2 x } } } - { 6 x – 1 } $$

مثال ۳

پاسخ عمومی معادله دیفرانسیل زیر را بدست آورید.

$$ \large y ^ { \prime \prime } – 5 y ^ { \prime } + 4 y = { e ^ { 4 x } } $$

معادله همگن مرتبط برابر است با:

$$\large y ^ { \prime \prime } – 5 y ^ { \prime } + 4 y =0$$

بنابراین معادله مشخصه و ریشه‌های آن برابرند با:

$$\large \begin {align*} { k ^ 2 } – 5k + 4 = 0 & \Rightarrow{D = 25 – 4 \cdot 4 = 9 \; \; } \\ & \Rightarrow { { k_ { 1 , 2 } } = \frac { { 5 \pm \sqrt 9 } } { 2 } }= { \frac { { 5 \pm 3 } } { 2 } } = { 4,1 } \end {align*} $$

در نتیجه پاسخ عمومی معادله همگن برابر است با:

$$\large { y_ 0 } \left ( x \right ) = { C _ 1 } { e ^ { 4 x } } + { C _ 2 } { e ^ x } $$

در رابطه فوق مقادیر $$C_1$$ و $$C_2$$ اعدادی ثابت هستند. در مرحله بعد باید پاسخ خصوصی معادله ناهمگن را بیابیم. توجه داشته باشید که $$4$$ هم یکی از ریشه‌های معادله مشخصه و هم توان نمایی ترمِ ناهمگن است. بنابراین پاسخ خصوصی را باید در $$x$$ ضرب کرد. در حقیقت شکل پاسخ خصوصی به صورت زیر خواهد بود.

$$ \large { y _ 1 } = A x { e ^ { 4 x } } $$

در نتیجه مشتق اول و دوم تابع به صورت زیر بدست می‌آیند.

$$ \large \begin {gather*} { { y ^ { \prime } _ 1 } = { \left( { A x {e ^ { 4x } }} \right ) ^ \prime } } = { A { e ^ { 4 x } } + 4 A x { e ^ { 4 x } } } = { \left ( { A + 4 A x } \right ) { e ^ {4 x }}} \\\\ {{ y ^ { \prime \prime}_1} = {\left[ {\left( {A + 4Ax} \right){e^{4x}}} \right]^\prime } } = {4A{e^{4x}} + \left( {4A + 16Ax} \right){e^{4x}} } = {\left( {8A + 16Ax} \right){e^{4x}}} \end {gather*} $$

با قرار دادن تابع $$y$$ در نظر گرفته شده و مشتقاتش در معادله اصلی، ثابت $$A$$ به صورت زیر بدست خواهد آمد.

$$\large \begin {align*} \require{cancel} \left ( { 8 A + 16 A x } \right ) { e ^ { 4 x } } & - { 5 \left( { A + 4 A x } \right) { e ^ {4 x } } } + { 4 A x { e ^ { 4x } } } = { e ^ { 4 x } } \\ & \Rightarrow { { 8 A + \cancel{16Ax} – 5A }}-{{ \cancel{20Ax} + \cancel { 4 A x } = 1 \;\; } } \\\\ & \Rightarrow { 3 A = 1} \\\\ & \Rightarrow {A = \frac{1}{3} } \end {align*} $$

بنابراین پاسخ خصوصی معادله دیفرانسیل برابر است با:

$$ \large { y _ 1 } = \frac { x }{3 } { e ^ { 4 x } } $$

نهایتا پاسخ عمومی معادله ناهمگن برابر با عبارت زیر بدست می‌آید.

$$\large \begin {align*} y & = { y _ 0 } + { y _1 } \\ & = { C _1 } { e ^ { 4 x } } + { C_ 2} { e ^ x } + \frac { x } { 3 } { e ^{ 4 x } } \end {align*} $$

مثال ۴

پاسخ معادله دیفرانسیل زیر را بیابید.

$$\large y ^ { \prime \prime } – 7 y ^{\prime} + 12 y = 8\sin x + { e ^ { 3 x } } $$

فیلم آموزش ریاضی مهندسی

اینجا کلیک کنید

بدیهی است که معادله همگن مرتبط، به صورت زیر بیان می‌شود:

$$\large y ^ { \prime \prime } – 7y ^ { \prime } + 12 y = 0 $$

بنابراین معادله مشخصه مربوط به معادله همگن برابر است با:

$$\large \begin {align*} { { k ^ 2 } – 7k + 12 = 0 \; \; } & \Rightarrow { D = 49 – 4 \cdot 12 = 1 \; \; } \\\\ & \Rightarrow { { k_ { 1 , 2 } } = \frac { {7 \pm 1}}{2} = 4 , 3 } \end {align*} $$

بنابراین پاسخ عمومی معادله همگن برابر است با:

$$ \large \begin {align*} { y _ 0 } \left ( x \right ) = { C _1 } { e ^ {4 x } } + {C _ 2 } { e ^ { 3 x } } \end {align*} $$

حال به منظور بدست آوردن شکل پاسخ خصوصی، باید به فرمت ترم سمت راست نگاه کرد. همان‌طور که می‌بینید این تابع ترکیبی از دو تابع سینوسی و نمایی است؛ لذا پاسخ خصوصی حدس زده شده نیز به صورت ترکیبی از این دو تابع در نظر گرفته می‌شود. در حقیقت شکل کلی پاسخ خصوصی به صورت زیر است.

$$\large { y _ 1 } \left ( x \right ) = { y _ 2 } \left ( x \right ) + { y _ 3 } \left ( x \right ) $$

در عبارت در نظر گرفته شده در بالا $$y_۲$$، پاسخ خصوصی $$ y ^ { \prime \prime } – 7 y ^{\prime} + 12 y = 8 \sin x $$ و $$y_1$$، پاسخ خصوصی $$ y^{\prime\prime} – 7y’ + 12y=e^{3x} $$ را نمایندگی می‌کند. در ابتدا تابع $$ { y _ 2 } \left ( x \right ) $$ را بدست می‌آوریم. شکل کلی این تابع به صورت زیر است.

$$ \large { { y _ 2 } \left ( x \right ) } = { A \cos x + B \sin x } $$

در نتیجه مشتقات اول و دوم این تابع برابرند با:

$$\begin {gather*} {{ y ^ { \prime } _ 2 } \left ( x \right ) = – A \sin x + B \cos x } \\\\ \kern-0.3pt { { y ^ { \prime \prime } _ 2 } \left ( x \right ) = – A \cos x – B \sin x } \end {gather*} $$

با قرار دادن مشتقات فوق در معادله اصلی داریم:

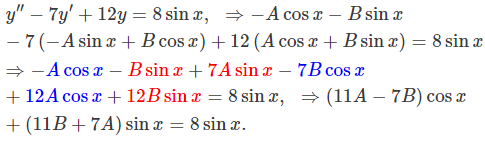
بنابراین مقادیر $$A$$ و $$B$$ برابرند با:

$$\large {\left\{ \begin{array}{l}
11A – 7B = 0\\
11B + 7A = 8
\end{array} \right. \;\;} \Rightarrow {\left\{ \begin{array}{l}
A = \frac { { 28 } } { { 85 } } \\
B = \frac { { 44 } }{ {85 } }
\end{array} \right. }$$

نهایتا پاسخ خصوصیِ $$ y _ 2 ( x ) $$، برابر با عبارت زیر بدست می‌آید.

$$ \large { y _ 2 } \left ( x \right ) = { \frac { { 28 } } { { 85 } } } \cos x + { \frac { { 44 } }{ { 85 } } } \sin x $$

حال باید تابع $$ y _ 3 ( x ) $$ را بدست آورد. توجه داشته باشید که یکی از ریشه‌های معادله مشخصه برابر با $$3$$ بود. لذا پاسخِ فرضی $$ y _ 3 ( x ) $$ باید متغیر $$x$$ را در خود داشته باشد. در نتیجه $$ y _ 3 ( x ) $$ را به صورت زیر در نظر می‌گیریم.

$$\large { y _ 3 } \left ( x \right ) = A x { e ^ { 3 x } } $$

در نتیجه همچون $$ y _ 2 ( x ) $$، مشتقات $$ y _ 3 ( x ) $$ را نیز محاسبه کرده و با قرار دادن آن در معادله ناهمگن، ثابت $$A$$ بدست می‌آید (این بخش را به شما خواننده گرامی واگذار می‌کنیم). نهایتا پاسخ خصوصی برابر با عبارت زیر بدست خواهد آمد.

$$\large { y _ 3 } \left ( x \right ) = – x { e ^ { 3 x } } $$

نهایتا با بدست آمدن پاسخ‌های خصوصی، پاسخ عمومی معادله ناهمگن نیز برابر با عبارت زیر بدست خواهد آمد.

$$\large \begin {align*} y & = { y _ 0 } + { y _ 2 } + { y _ 3 } \\~\\ & = { C _ 1 } { e ^ { 4 x } } + {C _ 2 } { e ^ { 3 x} } + \frac { { 28 } } { { 85 } } \cos x + { \frac { { 44 } } { { 85 } } \sin x } - { x { e ^ {3 x } } } \end {align*} $$

معمولا از این دو روش به منظور بدست آوردن پاسخ عمومی معادله دیفرانسیل ناهمگن استفاده می‌شود.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضیات مهندسی (مرور – تست کنکور ارشد)
• مجموعه آموزش‌های ریاضی و فیزیک
• معادلات دیفرانسیل مرتبه دوم — به زبان ساده
• معادلات دیفرانسیل ناهمگن - به زبان ساده
• معادله دیفرانسیل حرکت — از صفر تا صد

^^

فیلم‌ های آموزش معادلات دیفرانسیل مرتبه دوم ناهمگن — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی معادلات دیفرانسیل مرتبه دوم ناهمگن

فیلم آموزشی حل چند مثال از معادلات دیفرانسیل مرتبه دوم ناهمگن