مرکز آنی دوران — به زبان ساده

پیش ‌تر در وبلاگ فرادرس مفاهیم مرتبط با حرکت دایره‌ای، سرعت زاویه‌ای و دیگر مفاهیم سینماتیکی توضیح داده شدند. در این بخش قصد داریم تا مفهومی را توضیح دهیم که از آن در اکثر ربات‌ها و مکانیزم‌های صنعتی استفاده می‌شود. این مفهوم تحت عنوان مرکز آنی دوران شناخته می‌شود.

البته پیشنهاد می‌شود قبل از مطالعه این مطلب، مطالب حرکت دایره‌ای، سرعت و بردار را مطالعه فرمایید.

مفهوم مرکز آنی دوران

برای یک جسم صلب با استفاده از مفهوم مرکز آنی می‌توان سرعت خطی یا زاویه‌ای نقاط مجهول را بدست آورد. مرکز آنی دوران، محلی مجازی است که جسم صلب در لحظه، حول آن دوران می‌کند. در حالت کلی برای حل مسائل مکانیزم‌ها سه حالت وجود دارد که در آن‌ها می‌توان از مرکز آنی دوران استفاده کرد.

فیلم آموزش فیزیک 1 دانشگاهی با رویکرد حل مساله در فرادرس

کلیک کنید

حالت اول

جسمی صلب را مطابق با شکل زیر در نظر بگیرید که در یک صفحه در حال حرکت است. فرض کنید سرعت v_B و تنها جهت A داده شده و هدف بدست آوردن اندازه سرعت v_A است.

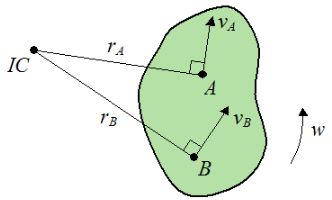
در شکل فوق نماد‌های استفاده شده موارد زیر هستند:

• v_A: سرعت نقطه A در لحظه نشان داده شده
• v_B: سرعت نقطه B در لحظه نشان داده شده
• IC: محل تقاطع خطوط عمود بر دو سرعت
• r_A: فاصله نقطه A از IC در لحظه نشان داده شده
• r_B: فاصله نقطه B از IC در لحظه نشان داده شده
• w: سرعت زاویه‌ای جسم در لحظه نشان داده شده

به منظور بدست آوردن مرکز آنی یک جسم صلب، کافی است دو بردارِ سرعت از آن را داشته باشیم. اگر خطوط عمودِ به این دو بردار - که در این‌جا r_A و r_B هستند - را با هم قطع دهیم، نقطه بدست آمده همان مرکز آنی دوران است. در حقیقت در این لحظه، جسم حول IC دوران می‌کند.

با توجه به مفاهیم حرکت دورانی، سرعت نقطه A در این لحظه برابر است با:

$$\Large v _ A = w r _ A$$

به همین صورت سرعت نقطه B نیز برابر می‌شود با:

$$\Large v _ B = w r _ B$$

با ترکیب دو رابطه بالا، نسبت دو سرعت به صورت زیر قابل محاسبه خواهد بود.

$$\Large \frac { v _ A } { v _ B } = \frac { r _ A } { r _ B }$$
رابطه ۱

با استفاده از روش فوق می‌توان دو مجهول را بدست آورد.

مثال ۱

شکل زیر یک سیستم میل‌ لنگ پیستون را نشان می‌دهد. با استفاده از این مکانیزم می‌توان حرکت دایره‌ای را به حرکت خطی تبدیل کرد. سرعت نقطه B را با فرض معلوم بودن اندازه سرعت A بدست آورید.

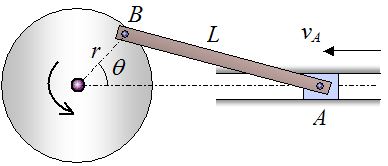
میل لنگ را به عنوان جسم در حال دوران در نظر بگیرید. همان‌طور که از شکل نیز معلوم است، نقطه B هم روی دیسک و هم روی میل لنگ قرار گرفته؛ لذا سرعت آن مماس به دیسک است. از طرفی نقطه A در سیلندر، در حال لغزش است. با رسم خطوط عمود به سرعت‌های A و B، مرکز آنی دوران مطابق با شکل زیر بدست می‌آید.

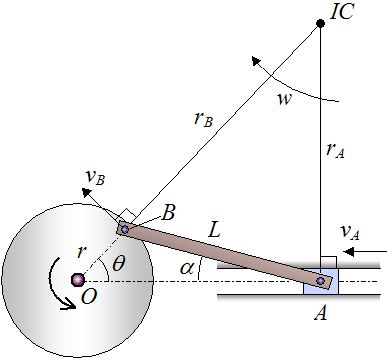
با استفاده از روابط مثلثاتی، فاصله OA برابر است با:

$$\Large O A = L \cos \alpha + r \cos \theta$$
رابطه ۲

از طرفی زاویه $$\large \alpha$$ نیز به صورت زیر بدست می‌آید.

$$\Large L \sin \alpha = r \sin \theta \Rightarrow \alpha = \sin ^ { - 1 } ( \frac { r } { L } \sin \theta )$$
رابطه ۳

با قرار دادن رابطه ۳ در رابطه ۲، فاصله مرکز پیستون و دیسک، به صورت زیر بدست می‌آید.

$$\Large O A = L \cos ( \sin ^ { - 1 } ( \frac { r } { L } \sin \theta ) ) + r \cos \theta$$

با بدست آمدن طول OA، طول r_B نیز به صورت زیر بدست می‌آید.

$$\Large r _ B = \frac { O A } { \cos \theta } - r$$

هم‌چنین با توجه به شکل طول r_A برابر با رابطه زیر بدست می‌آید.

$$\Large r _ A = O A \tan \theta$$

در نهایت با استفاده از رابطه ۱ و طول بدست آمده برای r_A، سرعت B نیز به صورت زیر بدست می‌آید.

$$\Large \frac { v _ B } { v _ A } = \frac { r _ B } { r _ A } \Rightarrow v _ B = v _ A \frac { O A - r \cos \theta } { O A \sin \theta }$$

شاید این سوال را ذهن داشته باشید که در صورت صفر بودن $$\large \theta$$ سرعت $$\large v _ B = \infty$$ بدست می‌آید. باید توجه داشته باشید که در این حالت، $$\large r _ A = 0$$ بوده و نمی‌توان از رابطه ۱ استفاده کرد.

نکته: در حالت اول، شرایط خاصی نیز ممکن است وجود داشته باشد. اگر سرعت نقاط A و B در یک جهت باشند، در این صورت r_A و r_B یکدیگر را در بینهایت قطع می‌کنند. بنابراین مرکز آنی در بینهایت قرار داشته و جسم در لحظه مدنظر حرکتی انتقالی را انجام می‌دهد.

حالت دوم

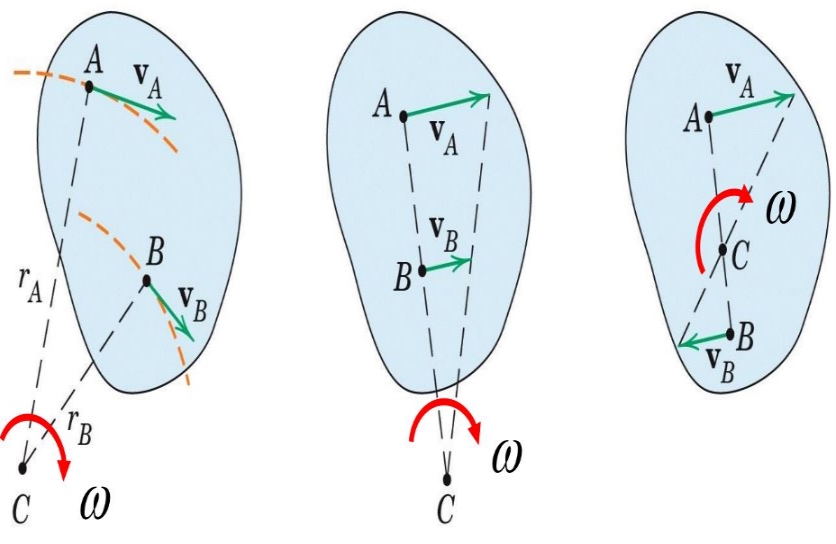
جسمی صلب را مطابق با شکل زیر در نظر بگیرید.

فیلم آموزش مکانیک تحلیلی 1 مرور و حل مثال در فرادرس

کلیک کنید

فرض کنید سرعت‌های نقطه A و B معلوم بوده و می‌خواهیم اندازه سرعت زاویه‌ای w را بدست آوریم.

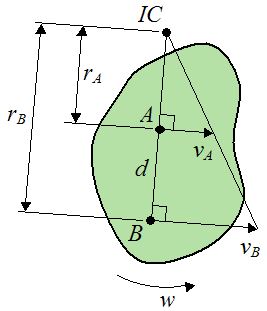
همان‌طور که در شکل فوق نیز نشان داده شده در این حالت، سرعت‌های A و B در یک جهت هستند. در این حالت برای بدست آوردن مرکز آنی دوران، ابتدا دو بردار سرعت را به هم وصل کرده و نقطه تقاطع آن با خطوط عمود به سرعت‌ها معادل مرکز آنی دوران جسم در لحظه مدنظر است. با استفاده از قوانین تالس (یا قوانین حرکت دایره‌ای)، رابطه زیر را می‌توان نوشت:

$$\Large \frac { v _ B - v _ A } { d } = \frac { v _ B } { r _ B } = \frac { v _ A } { r _ A }$$
رابطه ۴

همچنین سرعت نقطه A نیز به صورت زیر بدست می‌آید.

$$\Large v _ A = w r _ A$$
رابطه ۵

به همین صورت سرعت نقطه B نیز برابر است با:

$$\Large v _ B = w r _ B$$
رابطه ۶

با ترکیب روابط ۴، ۵ و ۶ سرعت زاویه‌ای برابر با رابطه زیر بدست می‌آید.

$$\Large \boxed {w = \frac { v _ B - v _ A } { d }}$$

مثال ۲

چرخی به شعاع R را در نظر بگیرید که سرعت نقاط A و B در آن به صورت زیر است. مقدار سرعت زاویه‌ای را به صورت پارامتری بدست آورید.

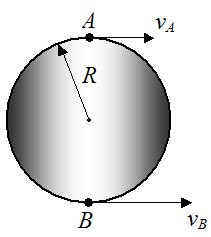
فاصله بین نقاط A و B برابر با ۲R است. بنابراین اندازه سرعت زاویه‌ای در این لحظه برابر است با:

$$\Large { w = \frac { v _ B - v _ A } { 2 R } }$$

حالت سوم

در این حالت نیز جسمی صلب را مطابق با شکل زیر در نظر بگیرید. تفاوت این حالت با حالت دوم در جهت سرعت‌ها است. همان‌طور که می‌بینید سرعت‌ها موازی ولی در جهتی مخالف یکدیگر هستند.

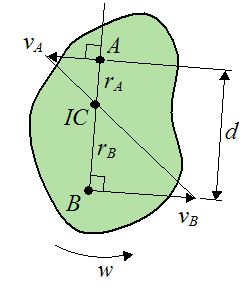
در این حالت نیز ابتدای بردار‌ها را به یکدیگر وصل کرده و تقاطع آن با خط اتصال دو نقطه یا AB، برابر با مرکز آنی است. با استفاده از تشابه دو مثلث تشکیل شده، می‌توان گفت:

$$\Large \frac { v _ B + v _ A } { d } = \frac { v _ B } { r _ B } = \frac { v _ A } { r _ A }$$

در این صورت سرعت نقاط A و B به صورت زیر بدست می‌آیند.

$$\Large v _ A = w r _ A$$

$$\Large v _ B = w r _ B$$

با ترکیب سه معادله بالا، سرعت زاویه‌ای برابر می‌شود با:

$$\Large { w = \frac { v _ B + v _ A } { d } }$$

مثال ۳

دیسکی را به شعاع R در نظر بگیرید که سرعت‌های دو نقطه از آن مطابق با شکل زیر باشند. در این صورت مقدار سرعت زاویه‌ای چقدر خواهد بود؟

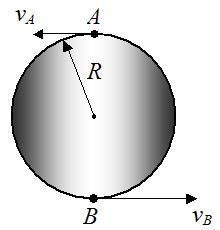
فاصله بین دو نقطه A و B برابر با 2R است. بنابراین سرعت زاویه‌ای دیسک نیز به صورت زیر بدست می‌آید.

$$\Large w = \frac { v _ A + v _ B } { 2 R }$$

در این مطلب مفاهیم پایه‌ای مرکز آنی دوران توضیح داده شدند. در آینده کاربرد این مفهوم در طراحی مکانیزم‌ها را توضیح خواهیم داد.
در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• حرکت دایره‌ای -- به زبان ساده
• عدد ناسلت (Nusselt Number) — به زبان ساده
• تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد

^^