محاسبات ماتریسی در اکسل – از صفر تا صد

در بسیاری از شاخه‌های ریاضی و بخصوص حل دستگاه و «جبر خطی» (Linear Algebra)، «ماتریس‌» (Matrix) و محاسبات مربوط به آن حضور دارند. شاید بتوان محاسبات ماتریسی را به شکل تعمیم محاسبات عددی در فضای چند بُعدی در نظر گرفت. در این نوشتار قصد داریم محاسبات ماتریسی در اکسل را یادآوری کنیم. به این ترتیب با توجه به فراگیری اکسل به عنوان یک ابزار محاسباتی در بین همه کسانی که به نوعی با حساب و کتاب سروکار دارند، توابع و فرمول‌هایی برای انجام عملیات جبرخطی یا محاسبات ماتریسی در اکسل معرفی می‌شود.

برای آشنایی بیشتر با ماتریس و انجام محاسبات روی آن، نوشتارهای ماتریس‌ها — به زبان ساده و معکوس ماتریس یا ماتریس وارون – به زبان ساده را مطالعه کنید. همچنین خواندن مطالب ضرب ماتریس‌ها – به زبان ساده و دترمینان یک ماتریس — به زبان ساده نیز توصیه می‌شود.

محاسبات ماتریسی در اکسل

ماتریس، یک شیوه ریاضیاتی برای نمایش چندین مقدار عددی است که با یکدیگر ارتباط دارند. به کمک ماتریس‌ها، روابط بین اعداد و توابع در فضای اعداد حقیقی، توسعه یافته و قضیه‌های ریاضی در فضای چند بُعدی نیز قابل استفاده می‌شوند.

همین موضوع باعث می‌شود که محاسبات ماتریسی از اهمیت زیادی برخوردار باشند. از آنجایی که در این نوشتار قرار است در مورد نحوه انجام محاسبات ماتریسی در اکسل بحث کنیم، بعضی از عملیات جبری روی ماتریس‌ها را مرور کرده، سپس به نحوه اجرای آن‌ها در اکسل خواهیم پرداخت.

عملیات ماتریسی

مقادیر به شیوه خاصی در یک ماتریس معرفی و نمایش داده می‌شوند. فرض کنید اعداد ۱ تا 6 را به صورت زیر نشان داده‌ایم و آن را  $$A$$ نامیده‌ایم.

$$\large A = \begin{bmatrix} 1 & 2 & 3 \\ \large 4 & 5 & 6 \end{bmatrix}$$

فیلم آموزش اکسل – محاسبات ریاضی و ماتریسی با Microsoft Excel 2016 در فرادرس

کلیک کنید

ساختاری که دیدید، یک ماتریس (Matrix)  نام دارد. مشخص است که اعداد به صورت سطری و ستونی در یک کادر قرار گرفته‌اند. با توجه به این که ماتریس $$A$$ دارای دو سطر و سه ستون است، آن را یک ماتریس $$2 \times 3$$ می‌گویند و می‌نویسند $$A_{2 \times 3}$$. چنین ماتریسی را گاهی ماتریس با ابعاد $$2 \times 3$$ نیز می‌شناسند. به هر یک از این مقادیر درون ماتریس، مولفه یا «درایه» (Elements) می‌گویند و به صورت $$a_{ij}$$ نشان می‌دهند که $$i$$ نشان دهنده شماره سطر و $$j$$‌ نیز شماره ستون درایه مربوطه را نشان می‌دهد.

نکته: اگر تعداد سطرها و ستون‌های یک ماتریس با هم برابر باشند، ماتریس را مربعی (square) می‌نامند. همچنین در یک ماتریس مربعی، درایه‌های $$a_{ii}$$ عناصر قطر اصلی ماتریس هستند. اگر عناصر خارج از قطر اصلی یک ماتریس، همگی صفر باشند، ماتریس حاصل، یک ماتریس «قطری» (Diagonal) نامیده می‌شود.

جمع و تقریق ماتریس‌ها

فرض کنید دو ماتریس $$A$$ و $$B$$ وجود دارند که هر دو دارای ابعاد یکسان (تعداد سطرها یکسان و تعداد ستون‌های یکسان) هستند. آنگاه جمع این دو ماتریس، ماتریسی است که درایه‌های آن، حاصل جمع درایه‌های هر یک از آن‌ها است.

$$\large A_{m\times n} = \begin{bmatrix} a_{11} & \ldots & a_{1n} \\ \large \vdots & \ddots & \vdots \\ \large a_{m1} & \dots & a_{mn} \end{bmatrix}$$

$$\large B_{m\times n} = \begin{bmatrix} b_{11} & \ldots & b_{1n} \\ \large \vdots & \ddots & \vdots \\ \large b_{m1} & \dots & b_{mn} \end{bmatrix}$$

به این ترتیب اگر ماتریس حاصل جمع را $$C$$ بنامیم، خواهیم داشت:

$$\large A_{m \times n} + B_{m \times n} = C_{m \times n}$$

که درایه‌های آن به صورت زیر است.

$$\large c_{ij} = a_{ij} + b_{ij}$$

نکته: برای تفریق دو ماتریس هم کافی است علامت جمع را به منهی تبدیل کرده و همان عملیات را انجام دهیم.

ضرب ماتریس‌ها

برای آنکه ضرب دو ماتریس $$A$$ و $$B$$‌ به صورت $$A \times B$$ امکان پذیر باشد، باید تعداد ستون‌های ماتریس $$A$$ با تعداد سطرهای ماتریس $$B$$ برابر باشد. در این صورت درایه‌های ماتریس نتیجه حاصل‌ضرب  یعنی $$C$$ به صورت زیر خواهد بود.

$$\large C_{m \times n} = A_{m \times l } \times B_{l \times n} , \;\;\; c_{ij} = \sum_{k=1}^l a_{ik} \times b_{kj}$$

ماتریس یکه، دترمینان و معکوس یک ماتریس

ماتریس مربعی را مرتبه $$n$$ که قطری و درایه‌های قطر اصلی برابر با ۱ باشد، «ماتریس یکه» (Identity Matrix) نامیده و آن را به صورت $$I_{n\times n}$$ نشان می‌دهند.

$$\large I _{n\times n} = \begin{bmatrix}1 & \ldots & 0 \\ \large \vdots & \ddots & \vdots \\ \large 0 & \dots & 1 \end{bmatrix}_{n \times n}$$

دترمینان (Determinant) یک ماتریس مربعی، قابل محاسبه بوده ولی شکل پیچیده‌ای دارد. برای مثال دترمینان ماتریس مربعی دو در دو به صورت زیر محاسبه می‌شود.

$$\large A_{2\times 2} = \begin{bmatrix}a & b \\ c & d \end{bmatrix} = \det(A) = |A| = (a\times d) - (b \times c)$$

به این ترتیب مشخص است که برای ماتریس دو در دو، دترمینان از طریق تفاضل حاصل‌ضرب قطر اصلی از حاصل‌ضرب قطر فرعی بدست می‌آید. همانطور که دیدید، دترمینان ماتریس $$A$$ را هم به صورت $$\det(A)$$ و هم به شکل $$|A|$$‌ نشان می‌دهند.

به همین ترتیب، معکوس یک ماتریس مربعی مثل $$A$$ را با $$A^{-1}$$‌ نشان داده و به صورت زیر معرفی می‌کنند.

$$\large A_{n \times n}^{-1} \times A_{n \times n} = A_{n \times n} \times A_{n \times n}^{-1} = I_{n\times n}$$

نکته: اگر جای سطرهای یک ماتریس را با ستون‌ها عوض کنیم، ماتریس ترانهاده (Transpose)، بدست می‌آید. براساس نحوه محاسبه دترمینان ماتریس، واضح است که دترمینان ترانهاده یک ماتریس دو در دو با دترمینان خود ماتریس برابر است.

واضح است که تعداد سطرهای یک ماتریس ترانهاده برابر با تعداد ستون‌های ماتریس اولیه است. به این معنی که اگر ماتریس اولیه $$A$$ دارای $$m \times n$$ سطر و ستون باشد، ترانهاده آن که با $$A'$$ نشان داده می‌شود، دارای $$n \times m$$ سطر و ستون است.

برای آشنایی با نحوه محاسبه معکوس یک ماتریس به نوشتارهای مرتبط با این موضوع در مجله فرادرس مراجعه کنید. البته به این موضوع توجه داشته باشید که تعریف معکوس مربوط به ماتریس‌های مربعی است. در غیر این صورت از تعریف «معکوس تعمیم یافته» (Generalized Inverse Matrix) استفاده می‌شود که در نوشتارهای دیگر در مورد آن صحبت خواهیم کرد.

توابع مرتبط با محاسبات ماتریسی در اکسل

پس از اینکه تعریف ماتریس‌ها و شیوه انجام بعضی از محاسبات پایه‌ای روی آن‌ها را فرا گرفتید، زمان آن رسیده که با توابع و محاسبات ماتریسی در اکسل آشنا شوید.

فیلم آموزش رایگان اکسل Excel – محاسبات ریاضی و ماتریسی – ویژه ناشنوایان در فرادرس

کلیک کنید

ایجاد ماتریس یکه در اکسل

یکی از توابع بسیار جالب محاسبات ماتریسی در اکسل، ایجاد ماتریس یکه با رتبه دلخواه است. برای این کار از تابع MUNIT به شکل زیر استفاده می‌شود. پارامتر این تابع همانطور که می‌بینید، ابعاد یا اندازه ماتریس یا ($$n$$) است که به نام dimension در این تابع دیده می‌شود.

$$\large MUNIT(dimension)$$

برای مثال اگر مقدار پارامتر در این تابع را ۲ قرار دهیم، یک ماتریس مربعی $$2 \times 2$$‌ ایجاد شده که عناصر قطر اصلی برابر با ۱ بوده و در مقابل همگی داریه‌های خارج از قطر اصلی، صفر هستند. برای ایجاد چنین ماتریسی، مراحل زیر را انجام می‌دهیم.

1. یک ناحیه مربعی با دو سطر و دو ستون را از کاربرگ اکسل انتخاب می‌کنیم (در اینجا سلول‌های A1 تا B2 انتخاب شده‌اند).
2. تابع MUNIT را وارد کرده و پارامتر dimension را ۲ تعیین می‌کنیم.
3. برای ثبت این تابع درون ناحیه انتخاب شده، کلیدهای ترکیبی Ctrl+Shift+Enter را همزمان فشار می‌دهیم.

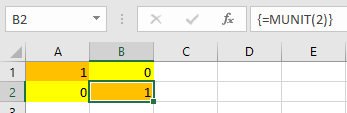
همانطور که در تصویر ۱ قابل مشاهده است، به کمک تابع معرفی شده، یک ماتریس قطری دو در دو با درایه‌های ۱ روی قطر اصلی ایجاد شده است. توجه داشته باشید که تعداد سلول‌های انتخابی در گام ۱ باید متناسب با پارامتر dimension باشد. برای مثال اگر بخواهید یک ماتریس قطری مرتبه ۳ ایجاد کنید باید ناحیه مربعی با سه سطر و سه ستون را انتخاب کرده سپس تابع munit را با پارامتر ۳ به کار برید.

نکته:‌ چنانچه مقدار پارامتر این تابع کمتر از 1 باشد، اکسل پیغام خطای !value# را نشان می‌دهد.

محاسبه جمع و تفریق دو ماتریس در اکسل

متاسفانه در اکسل برای جمع یا تفریق دو ماتریس، تابعی وجود ندارد. ولی به راحتی با استفاده از عمل جمع معمولی در اکسل می‌توانیم حاصل جمع یا تفریق دو ماتریس را بدست آوریم. همانطور که گفته شد، برای جمع یا تفریق دو ماتریس، لازم است که هر دو ماتریس، هم رتبه یا هم مرتبه باشند. در نتیجه با اجرای مراحل زیر می‌توانیم حاصل جمع یا تفریق آن‌ها را در اکسل بدست آوریم.

1. یک ناحیه خالی از کاربرگ را به ابعاد هر یک از ماتریس‌ها، انتخاب کنید.
2. بدون آنکه از حالت انتخاب خارج شوید، با زدن کلید مساوی (=) فرمول نویسی را آغاز کنید.
3. ناحیه مربوط به ماتریس اول را انتخاب کرده و کلید بعلاوه (+) یا منفی (-) را بزنید.
4. ناحیه مربوط به ماتریس دوم را انتخاب کنید.
5. برای ثبت حاصل جمع یا تفریق، کلیدهای ترکیبی Ctrl+Shift+Enter را بزنید.

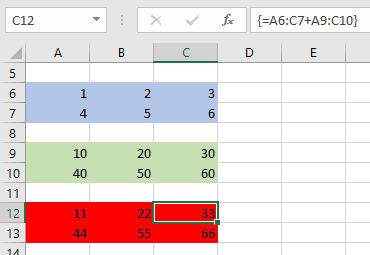
این کار در تصویر 2 صورت گرفته است. مشخص است که ناحیه آبی رنگ مربوط به ماتریس اول و ناحیه سبز رنگ نیز ماتریس دوم را نشان می‌دهد. حاصل جمع این دو ماتریس نیز در سلول‌های قرمز رنگ محاسبه شده است.

نکته: متاسفانه اکسل کنترلی روی ابعاد ماتریس‌ها برای جمع یا تفریق انجام نمی‌دهد ولی درایه‌های حاصل جمع ماتریس‌های غیر هم رتبه، که قابل محاسبه نیستند، را با مقدار خطای !N/A# نشان می‌دهد.

محاسبه ضرب دو ماتریس در اکسل

خوشبختانه ضرب دو ماتریس در اکسل دارای تابع مخصوصی است که محاسبات گفته شده برای ضرب را به طور خودکار انجام می‌دهد. فرض کنید قرار است ماتریس $$A$$ که در ناحیه A1 تا D2 ثبت شده در ماتریس $$B$$ که در ناحیه A4 تا C7 قرار گرفته، ضرب و حاصل $$A \times B$$ بدست آید.

فیلم آموزش اکسل – ابزارهای کاربردی Excel + گواهینامه در فرادرس

کلیک کنید

همانطور که می‌بینید ماتریس $$A$$ دارای دو سطر و چهار ستون است. همچنین ماتریس $$B$$ نیز چهار سطر و سه ستون دارد. در نتیجه امکان ضرب این دو ماتریس وجود دارد و حاصل ضرب باید یک ماتریس $$2 \times 3$$ باشد. به این معنی ماتریس حاصل عملیات این ضرب باید ۲ سطر و ۳ ستون داشته باشد.

به منظور محاسبه ضرب دو ماتریس در اکسل از تابع MMULT استفاده می‌کنیم. شکل دستوری این تابع به صورت زیر است.

$$\large MMULT(array1, array2)$$

پارامتر array1، بیانگر ناحیه‌ای است که به عنوان ماتریس اول در نظر گرفته شده و array2 نیز ماتریس بعدی در عمل ضرب خواهد بود.  به ابعاد این پارامترها هنگام استفاده از تابع MMULT توجه داشته باشید.

برای انجام این محاسبه گام‌های زیر را بر می‌داریم:

1. ناحیه پاسخ (در اینجا از A10 تا C11) را انتخاب کنید.
2. تابع MMULT را از لیست توابع ریاضی و مثلثات (Math & Trig) داخل برگه Formulas از بخش Function Library انتخاب کنید.
3. پارامترهای تابع را مطابق ناحیه مربوط به ماتریس اول و دوم، مشخص کنید. با توجه به توضیحات قبلی، در اینجا پارامتر اول، ناحیه A1:D2 است و پارامتر دوم نیز A4:C7 خواهد بود.
4. برای ثبت این تابع، از کلیدهای ترکیبی Ctrl+Shift+Enter استفاده کنید.

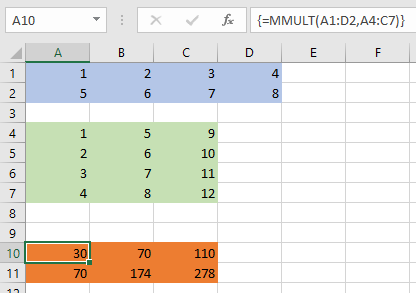
همانطور که دیده می‌شود، ماتریس $$A$$ با رنگ آبی و ماتریس $$B$$ نیز با رنگ سبز مشخص شده است. نتیجه حاصل‌ضرب این دو ماتریس نیز در ناحیه نارنجی رنگ قرار گرفته است.

توجه داشته باشید که اگر ابعاد ماتریس‌های array1 و array2 برای ضرب مناسب نباشند، اکسل فقط درایه‌هایی که قابل محاسبه بوده‌اند را بدست آورده و بقیه مقادیر مربوط به ناحیه پاسخ را با !N/A# پر می‌کند.

نکته: با توجه به ابعاد ماتریس‌ها مشخص است که اگر ضرب $$A \times B$$ امکان‌پذیر باشد دلیل ندارد که $$B \times A$$ نیز قابل اجرا باشد. در نتیجه ضرب ماتریس‌ها، برعکس ضرب اعداد، قابلیت جابجایی ندارد.

محاسبه ترانهاده ماتریس در اکسل

همانطور که گفته شد، با تغییر درایه‌های مربوط به سطرها و قرار دادن آن‌ها در ستون‌های یک ماتریس، ترانهاده آن ماتریس تولید می‌شود. برای انجام این کار تابعی در اکسل در نظر گرفته شده است. به این منظور بهتر است از تابع TRANSPOSE استفاده کنید که شکل دستوری آن در ادامه دیده می‌شود.

$$\large TRANSPOSE(array)$$

واضح است که array، ماتریس (یا برداری) است که قرار است جای سطرها و ستون‌هایش عوض شود. برای انجام محاسبات مربوط به ترانهاده یک ماتریس در اکسل مراحل زیر باید طی شوند.

1. ناحیه مناسب برای ترانهاده ماتریس جدید را از یک کاربرگ، انتخاب کنید. مطابق با تصویر زیر، ماتریس اولیه دو سطر و پنج ستون دارد، پس باید برای محاسبه ترانهاده آن، یک ناحیه با پنج سطر و دو ستون انتخاب شود.
2. تابع TRANSPOSE را از برگه Formula و قسمت Function Library از گروه Math & Trig انتخاب کنید.
3. ناحیه مربوط به ماتریس اولیه را به عنوان پارامتر انتخاب کنید.
4. کلیدهای ترکیبی Ctrl+Shift+Enter را به منظور ثبت این تابع از روی صفحه کلید فشار دهید.

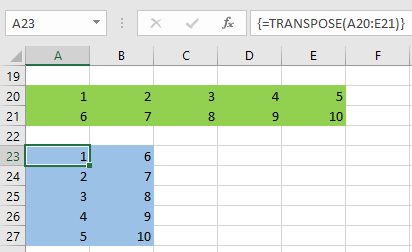
نتیجه مطابق با تصویر 4 محاسبه خواهد شد. ترانهاده ماتریس سبز رنگ، با انجام این محاسبات در ناحیه‌ای که در تصویر ۴ با رنگ آبی مشخص شده، دیده می‌شود.

محاسبه دترمینان ماتریس در اکسل

یکی دیگر از توابع مربوط به محاسبات ماتریسی در اکسل محاسبه دترمینان یک ماتریس است که بدست آوردن آن بدون رایانه‌ها بخصوص برای ماتریس‌های بزرگ، کاری سخت و طولانی است. خوشبختانه اکسل به کمک تابع MDETERM این کار را برایمان انجام می‌دهد. شکل دستوری این تابع به صورت زیر است.

$$\large MDETERM(array)$$

مشخص است که پارامتر array، به ماتریسی اشاره دارد که قرار است دترمینان آن محاسبه شود. در تصویر ۵، کاربرگی را مشاهده می‌کنید که در آن دترمینان یک ماتریس دو در دو محاسبه شده است.

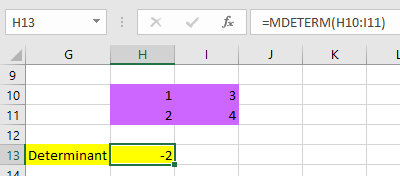
از آنجایی که مقدار دترمینان یک ماتریس، یک عدد خواهد بود، احتیاجی به ثبت این فرمول یا تابع به شکل ماتریسی (برداری) یا استفاده از کلیدهای ترکیبی Ctrl+Shift+Enter  نیست. در تصویر 6، دترمینان یک ماتریس بزرگ $$5 \times 5$$ را مشاهده می‌کنید. از آنجایی که سطرهای این ماتریس ترکیبی وابسته خطی نسبت به یکدیگر هستند، دترمینان آن صفر شده است.

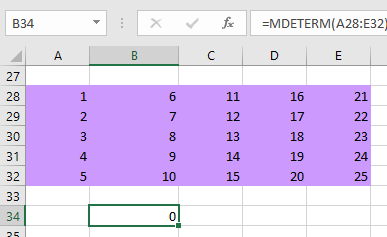
نکته: از آنجایی که بسط دترمینان ماتریس در اکسل به صورت سطری انجام می‌شود، ممکن است دترمینان ترانهاده بعضی از ماتریس‌ها با دترمینان خود ماتریس برابر نشود. این موضوع را براساس ترانهاده (Transpose) ماتریس قبلی،‌ مورد بررسی قرار می‌دهیم. در تصویر زیر، همان ماتریس مربوط به تصویر 6 را ترانهاده کرده و دترمینان را مطابق با تصویر ۷، محاسبه کرده‌ایم.

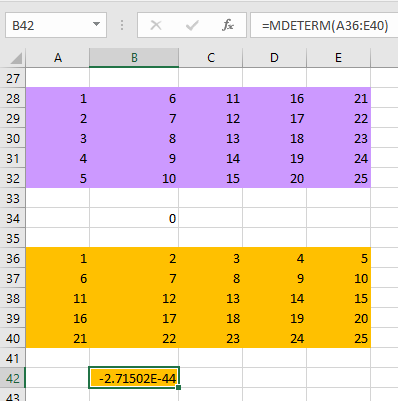
هر چند، مقدار دترمینان حاصل از ماتریس زرد رنگ، بسیار نزدیک به صفر است ولی به هر حال با صفر، اختلاف دارد. این مشکل می‌تواند ناشی از خطای محاسبات ماتریسی در اکسل باشد.

محاسبه معکوس یک ماتریس در اکسل

یکی از مشکلاتی که در انجام محاسبات ماتریسی وجود دارد، بدست آوردن معکوس یک ماتریس است که هم پیچیده و هم طولانی است. باز هم محاسبات ماتریسی در اکسل به کمک ما آمده و با تابع MINVERSE،‌ می‌توانیم معکوس یک ماتریس را محاسبه کنیم. البته شرط صفر نبودن دترمینان ماتریس نیز در اینجا باید لحاظ شود. به این ترتیب معکوس ماتریس، فقط برای ماتریس‌های مربعی و با دترمینان مخالف صفر صورت می‌پذیرد. شکل دستوری این تابع به صورت زیر است.

$$\large MINVERSE(array)$$

باز هم مشخص است که پارامتر array، همان ماتریسی است که باید معکوس آن در اکسل توسط این تابع محاسبه شود. در کاربرگ زیر قرار است ماتریسی مربعی که به رنگ آبی مشخص شده، معکوس شده و در ناحیه‌ای که به رنگ زرد درآمده، نمایش داده شود.

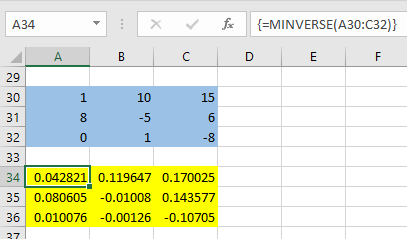
نکته: اگر ناحیه‌ای که به عنوان مکان مربوط به ماتریس معکوس در کاربرگ انتخاب کرده‌اید، متناسب با ماتریس اصلی نباشد، اکسل خطای !value# را نشان خواهد داد.

تقسیم دو ماتریس در اکسل

در جبر خطی برای تقسیم دو ماتریس، از عمل ضرب ماتریس اول در معکوس ماتریس دوم استفاده می‌شود. به این ترتیب اگر بخواهیم عمل محاسبات ماتریسی $$\dfrac{A}{B}$$ را برای دو ماتریس $$A$$ و $$B$$ انجام دهیم، به شکل زیر عمل می‌کنیم.

$$\large A \times B^{-1}$$

در اکسل هم برای انجام این کار باید ابتدا ماتریس $$B$$ را معکوس کرده سپس محاسبات مربوط به ضرب را دنبال کنیم. در کاربرگ زیر چنین عملی برای ماتریسی به رنگ سبز انجام شده و ماتریس آبی در معکوس ماتریس سبز رنگ، ضرب شده است.

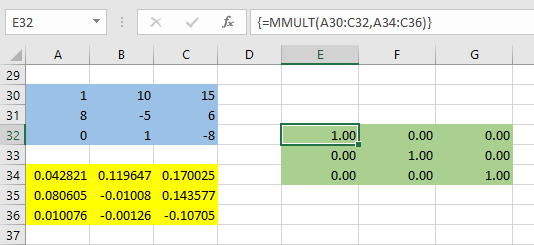
همانطور که در تصویر ۹ مشاهده می‌کنید، همیشه حاصل‌ضرب یک ماتریس در معکوس آن برابر با ماتریس یکه خواهد بود.

نکته: در مورد ترانهاده و دترمینان یک ماتریس اشاره کردیم که ممکن است حاصل ضرب ماتریس در معکوس آن توسط اکسل، کاملا یک ماتریس یکه نشود و درایه‌هایی با مقادیر نزدیک به صفر برای عناصر خارج از قطر اصلی بوجود آید. در تصویر ۹ برای نمایش صفر بودن درایه‌های خارج از قطر اصلی، قالب (format) مقادیر را از نوع Number انتخاب کرده و تعداد ارقام اعشار را ۲ رقم تعیین کرده‌ایم. به این ترتیب نتایج گرد شده و با دقت دو رقم اعشار نشان داده شده‌اند.

خلاصه و جمع‌بندی

در این نوشتار با نحوه انجام محاسبات ماتریسی در اکسل آشنا شدیم. به کمک مثال‌هایی نیز شیوه اجرای آن‌ها را در اکسل فرا گرفته و به کار بستیم. از آنجایی که عملیات ماتریسی بخصوص در ابعاد زیاد، وقت‌گیر و پیچیده خواهد شد، به کارگیری نرم‌افزارهای محاسباتی مانند اکسل، انجام چنین عملیاتی را ساده‌تر کرده و زمان کمتری را به خود اختصاص می‌دهد. در این بین محاسبه ماتریس معکوس توسط اکسل بسیار مورد توجه قرار گرفته است. البته به این نکته نیز باید توجه داشت که برای ثبت و انجام عملیات و محاسبات ماتریسی در اکسل باید از فشردن کلیدهای هم‌زمان Ctrl+Shift+Enter استفاده کنیم. در غیراینصورت نتیجه محاسبات، یک ماتریس یا بردار نخواهد بود.