قانون سوم ترمودینامیک – به زبان ساده
در مطالب گذشته وبلاگ فرادرس در مورد قوانین ترمودینامیک و همچنین مفهوم آنتروپی صحبت شد؛ از این رو پیشنهاد میشود قبل از مطالعه این مطلب، بهمنظور درک بهتر، این مقالات را مطالعه کنید. احتمالا تاکنون عبارات قانون اول و قانون دوم ترمودینامیک را شنیدهاید. اما از بین قوانین ترمودینامیک آنچه نسبت به بقیه ناشناختهتر محسوب میشود، قانون سوم ترمودینامیک است. از این رو در این مطلب قصد داریم تا این قانون را توضیح داده و مثالهایی نیز از آن ارائه دهیم.
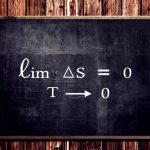

قانون سوم ترمودینامیک
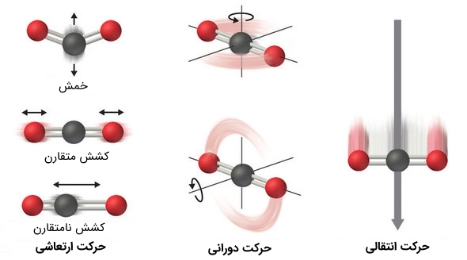
اتمها، مولکولها یا یونهایی که یک سیستم شیمیایی را تشکیل میدهند، میتوانند حرکتهایی مختلف، از جمله انتقالی، چرخشی و یا ارتعاشی داشته باشند. هرچه حرکت مولکولی یک سیستم بیشتر باشد، آنتروپی آن سیستم نیز بیشتر خواهد بود.
یک سیستمِ کاملا منظمشده تنها یک حالت را میتواند اختیار کند و آنتروپی آن نیز برابر با صفر است. تنها سیستمی که میتواند این حالت را داشته باشد، یک کریستال کامل منظم است که در دمای صفر مطلق () قرار گرفته است. در این وضعیت، مولکولها، اتمها و یونها بهطور کامل ثابت شده و هیچ گونه حرکتی را تجربه نمیکنند. در شکل زیر حرکتهایی نشان داده شده که یک ترکیب میتواند داشته باشد.
همانطور که بیان شد چنین سیستمی هیچ حرکتی نداشته و تنها میتوان آن را با استفاده از یک متغیر توصیف کرد. در حقیقت در این دما سیستم میتواند تنها یک ریزحالت را انتخاب کند. زیرحالتها در مکانیک آماری به پیکربندیهایی میگویند که یک سیستم میتواند اختیار کند. اگر تعداد ریزحالتهای مربوط به یک سیستم برابر با باشد، در این صورت آنتروپی چنین سیستمی را میتوان مطابق با رابطه زیر بیان کرد:
با توجه به رابطه فوق، برای سیستمی با یک ریزحالت () یا همان سیستم قرار گرفته در دمای صفر مطلق، مقدار زیر برای آنتروپی بدست میآید:
در عمل، صفر مطلق یک دمای ایدهآل محسوب میشود که غیر قابل دسترس است. همچنین یک کریستال با تنها یک ریزحالت نیز حالتی ایدهآل است که عملا قابل دستیابی نیست. با این وجود، ترکیبی از این دو حالت آرمانی، اساس قانون سوم ترمودینامیک را تشکیل میدهد. قانون سوم ترمودینامیک بیان میکند که آنتروپی هر ماده کریستالی کامل، در دمای صفر مطلق، برابر با صفر است. این قانون همچنین عنوان میکند که هرگز نمیتوان به دمای صفر مطلق دست یافت. در حقیقت در صفر مطلق هیچ فرآیند فیزیکی در یک سیستم رخ نمیدهد؛ در نتیجه آنتروپی آن به حداقل میرسد. این قانون را میتوان بهبیانی ریاضی، بهشکل زیر نشان داد.
قانون سوم ترمودینامیک دو نتیجه مهم را در پی دارد. اولین نتیجه این است که علامت آنتروپی هر ماده در دماهای بالاتر از صفر مطلق، عددی مثبت تعریف میشود. همچنین این نقطه، مرجعی ثابت را تعریف میکند که با استفاده از آن میتوان آنتروپی مطلق هر ماده را در دیگر دماها تعیین کرد. در این بخش، دو روش مختلف را برای محاسبه یک واکنش یا یک تغییر فیزیکی توضیح میدهیم. توجه داشته باشید که منظورمان از تغییر آنتروپی یک سیستم (یا یک واکنش) است.
در روش اول از تعریف ارائه شده از آنتروپی مطلق که توسط قانون سوم ترمودینامیک بیان شده، استفاده میکنیم. در روش دوم نیز از تابع حالت بودن آنتروپی (که در قانون دوم ترمودینامیک توضیح داده شده) در یک سیکل استفاده میکنیم.
آنتروپی حالت استاندارد
یک روش محاسبه برای یک واکنش، استفاده از مقادیر جدولی آنتروپی مولی استاندارد است. این مقدار برابر با آنتروپی یک مول از یک ماده است که در فشار ۱ بار قرار دارد. معمولا آنتروپی استاندارد مولی در مقدار درجه کلوین داده میشود و آن را با نماد زیر نشان میدهند.
واحد برابر با است. برخلاف انرژی درونی یا آنتالپی، آنتروپی مطلق را میتوان با اندازهگیری تغییرات آنتروپی در فاصله صفر تا ۲۹۸ درجه کلوین اندازهگیری کرد.
همانطور که در جدول زیر نیز نشان داده شده، برای موادی با جرم مولی و تعداد اتمهای تقریبا برابر، میتوان نامساوی زیر را بیان کرد:
| جامد | مایع | گاز | |||
| ماده | ماده | ماده | |||
| (الماس) | |||||
| (گرافیت) | |||||
| (کوارتز) | |||||
برای نمونه مقدار برای مایع آب برابر با است. این در حالی است که برای بخار آب بهصورت تقریبی برابر با است. بهطور مشابه برای گاز برابر با است. این در حالی است که همین مقدار برای (ید) که به شکل جامد است، برابر با اندازهگیری میشود.
مقادیر آنتروپی که نشاندهنده میزان جنب و جوش و حرکت اتمها و مولکولها است را میتوان در قالب سهفاز جامد، مایع و گاز درک کرد. در حقیقت اگر آنتروپی جسمی جامد افزایش یابد، با گذشت زمان حالت آن به مایع و نهایتا گاز تغییر خواهد کرد. در شکل زیر ارتباط بین حالت یک ماده و مقدار آنتروپی موجود در آن بهصورت کیفی نشان داده شده است.
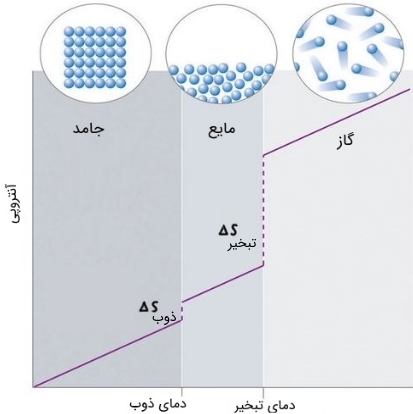
آنتروپی مطلق
آنتروپی مطلق یک ماده در هر دمایی بالاتر از صفر درجه، با استفاده از مقدار گرمایی محاسبه میشود که بهمنظور رساندن ماده مذکور از دمای صفر به دمای مدنظر، مورد نیاز است. اندازه دیفرانسیلی تغییرات آنتروپی برابر با مقادیر جزئی بدست میآید. بهمنظور محاسبه آنتروپی به این روش، دو نوع آزمایش انجام میگیرد.
مقادیر آنتالپی در هنگام تغییر فاز ماده باید اندازهگیری شود. در حقیقت ذوب شدن یک ماده جامد یا بخار شدن یک مایع منجر به افزایش ریزحالتهای ماده میشود. توجه داشته باشید که تغییر حالت ماده با دمای ثابت صورت میگیرد. با فرض اینکه تغییر آنتالپیِ ناشی از تغییر فاز یک ماده، برابر با باشد، در این صورت مقدار افزایش آنتروپی نیز برابر است با:
ظرفیت حرارتی که برای یک ماده تعریف میشود، برابر با مقدار انرژی مورد نیاز به منظور افزایش دما به اندازه ۱ واحد است. مقدار افزایش آنتروپی با توجه به این کمیت برابر است با:
توجه داشته باشید که خود ضریب نیز وابسته به دما است. بنابراین شکل دقیقتر رابطه فوق بهصورت زیر است.
معمولا با توجه به این که شکل کلی معلوم نیست، میتوان مقداری دیفرانسیلی را در بازه کوچک محاسبه کرده و با جمع زدن آنها مقدار نهایی افزایش آنتروپی را بدست آورد. در نمودار زیر مقدار مساحتهای هر بخش نشاندهنده افزایش آنتروپی در تغییر دمایی مذکور است. توجه داشته باشید که محور افقی مقادیر تغییرات دمایی را نشان میدهد.
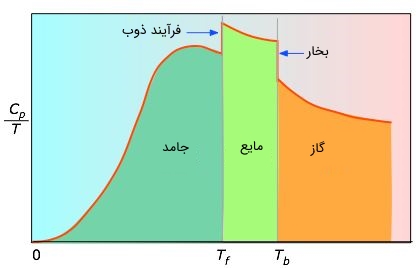
جالب است بدانید که مقادیر نزدیک به صفر بهصورت مستقیم اندازهگیری نمیشود و باید با استفاده از تئوری کوانتوم آن را اندازهگیری کرد. مقادیر آنتالپی در هر بخش اندازهگیری میشود و نهایتا مقدار مطلق آنتروپی در دمای با توجه به قانون سوم ترمودینامیک، برابر میشود با:
توجه داشته باشید که مقادیر فوق در بازههایی جداگانه جمع زده شدهاند.
محاسبه
میتوان با اندازهگیریهای حرارتی، وابستگی آنتروپی به دما را برای مواد مختلف اندازهگیری کرد. مقادیر آنتروپی استاندارد را با برچسب نمایش میدهند. این مقدار نشاندهنده آنتروپی یک مول از یک ماده در فشار ۱ بار و دمای ۲۹۸ کلوین است. مقدار استاندارد تغییر آنتروپی نیز با نماد نشان داده میشود. در این صورت مقدار تغییر آنتروپی استاندارد یک واکنش را میتوان مطابق با رابطه زیر بیان کرد:
در رابطه فوق Products و Reactants بهترتیب نشاندهنده فرآوردهها و واکنشدهندهها هستند. همچنین نیز نشاندهنده ضرایب استوکیومتری بوده که با موازنه واکنش بدست میآیند. برای نمونه فرض کنید هدف محاسبه برای واکنش زیر است.
در این صورت اندازه تغییر آنتروپی استاندارد را میتوان مطابق با رابطه زیر بیان کرد:
برای هر ماده مقادیر آنتروپی استاندارد در دمای درجه کلوین وجود دارد. مقادیر آنتروپی ارائه شده در جدول نشان میدهند که برای ترکیباتی که شکل ساختاری آنها مشابه با یکدیگر است، مقادیر آنتروپی استاندارد نیز بهصورت تقریبی با هم برابر است. از بین مواد کریستالی نیز آنهایی که ساختاری منظمتر دارند دارای آنتروپی کمتری هستند.
مثال ۱
با استفاده از اطلاعات ارائه شده در جدول فوق، تغییر آنتروپی استاندارد () برای واکنش یک مول اوکتان مایع با اکسیژن را بدست آورید.
بهمنظور بدست آوردن تغییر آنتروپی استاندارد در اولین گام باید واکنش را نوشته و آن را موازنه کرد. توجه داشته باشید که در صورت سوال از ما خواسته شده تا تغییر آنتروپی را برای یک مول از واکنشدهنده بدست آوریم. بنابراین موازنه باید به نحوی نوشته شود که تنها یک مول اوکتان در واکنش شرکت کند. البته در مطلب موازنه، نحوه بدست آوردن شکل استاندارد یک معادله شیمیایی بهطور کامل تشریح شده است. معادله واکنش یک مول اوکتان با اکسیژن برابر است با:
بهمنظور محاسبه تغییر آنتروپی استاندارد، کافی است مقادیر آنتروپی استاندارد واکنشدهندهها (Reactants) را از آنتروپی استاندارد فرآوردهها (Products) کم کرد. با انجام این کار مقدار تغییر آنتروپی برابر میشود با:
مثال ۲
تغییر آنتروپی استاندارد سوختن مول متانول را در دمای درجه کلوین بدست آورید.
معادله واکنش دو مول متانول () بهصورت زیر است.
همانند مثال ۱ کافی است مقادیر آنتروپی استاندارد فرآوردهها را از آنتروپی استاندارد واکنشدهندهها کم کنید. با انجام این کار، مقدار تغییر آنتروپی واکنش برابر است با:
با توجه به مقادیر ارائه شده در جدول، مقدار تغییر آنتروپی استاندارد برابر میشود با:
در مطالب آینده، در مورد ویژگیهای میکروسکوپی یک سیستم بیشتر بحث خواهیم کرد و معادلات آنتروپی بولتزمن را نیز توضیح خواهیم داد.
در صورتیکه مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزش نرمافزارهای مهندسی مکانیک
- مجموعه آموزشهای دروس مهندسی مکانیک
- آنتروپی — از صفر تا صد
- قانون اول ترمودینامیک — به زبان ساده
- قانون دوم ترمودینامیک – از صفر تا صد
^^












