روش سیمپلکس تجدید نظر شده | به زبان ساده

در آموزشهای قبلی مجله فرادرس، با روش سیمپلکس و همچنین، سیمپلکس دوگان آشنا شدیم. در این آموزش، «روش سیمپلکس تجدید نظر شده» (Revised Simplex Method) را معرفی خواهیم کرد.
روش سیمپلکس تجدید نظر شده
حل مسئله برنامهریزی خطی با یک کامپیوتر دیجیتال و به روش سیمپلکس معمولی، نیازمند ذخیره کل جدول سیمپلکس در حافظه کامپیوتر است که ممکن است برای مسائل بسیار بزرگ امکانپذیر نباشد. اما از طرفی لازم است که در هر تکرار جدول محاسبه شود.
روش سیمپلکس تجدید نظر شده یک اصلاح از روش اصلی است که برای اجرا در کامپیوتر اقتصادیتر است، زیرا فقط اطلاعات مورد نیاز فعلی را برای آزمایش و یا بهبود جواب فعلی محاسبه و ذخیره میکند. یعنی فقط به موارد زیر نیاز دارد:
- سطر ارزیابی خالص $$ \Delta _ j $$ برای تعیین متغیر غیرپایه که وارد پایه میشود.
- ستون لولا
- متغیرهای پایه فعلی و مقادیر آنها (ستون $$ X_ B $$) برای تعیین حداقل مقدار نسبت مثبت و سپس مشخص کردن متغیر پایه برای خروج از پایه.
اطلاعات بالا مستقیماً از معادلات اصلی با استفاده از وارون ماتریس پایه فعلی در هر تکرار به دست میآید.
دو فرم استاندارد برای روش سیمپلکس تجدید نظر شده وجود دارد:
- فرم استاندارد اول: در این فرم، فرض میشود که یک ماتریس یکه پس از تعیینِ فقط متغییرهای کمکی به دست میآید.
- فرم استاندارد دوم: اگر متغیرهای مصنوعی یا ساختگی برای یک ماتریس یکه لازم باشند، آنگاه از روش دو فازی سیمپلکس معمولی استفاده میشود، به گونهای که با متغیرهای ساختگی کمی متفاوتتر برخورد کند.
مراحل روش سیمپلکس تجدید نظر شده به فرم استاندارد
برای مثال، میخواهیم مسئله زیر را با استفاده از روش سیمپلکس تجدید نظر شده حل کنیم:
$$ \large \operatorname {Max}\;\;\;\;\; Z = 2 x _ { 1 } + x _ { 2 }
\\ \large
\operatorname {Subject to}\;\;\;\
\begin{array}{l}
3 x_{1}+4 x_{2} \leq 6 \\
6 x_{1}+x_{2} \leq 3 \\
\text { } x_{1}, x_{2} \geq 0
\end{array} $$
مسئله را به فرم زیر مینویسیم:
$$ \large \operatorname {Max} \;\;\;\;\;\;\; Z = 2 x _ { 1 } + x _ { 2 } + 0 s _ { 1 } + 0 s _ { 2 }
\\ \large
\operatorname {Subject to} \;\;\;\;\;\;
\begin{array}{l}
3 x_{1}+4 x_{2}+s_{1}=6 \\
6 x_{1}+x_{2}+s_{2}=3 \\
\text { } x_{1}, x_{2}, s_{1}, s_{2} \geq 0
\end{array} $$
گام ۱: مسئله را به فرم استاندارد اول مینویسیم:
- مطمئن میشویم که برای هر $$ i $$، نامساوی $$ b _ i \ge 0 $$ برقرار باشد.
- تابع هدف باید بیشینهساز باشد.
- از متغیرهای کمکی نامنفی برای تبدیل نامساویها به تساوی استفاده میکنیم.
تابع هدف را نیز به صورت یک قید تساوی مینویسیم. بنابراین، خواهیم داشت:
$$ \large \begin {array} { l }
Z - 2 x _ { 1 } - x _ { 2 } + 0 s _ { 1 } + 0 s _ { 2 } = 0 \\
3 x _ { 1 } + 4 x _ { 2 } + s _ { 1 } + 0 s _ { 2 } = 6 \\
6 x _ { 1 } + x _ { 2 } + 0 s _ { 1 } + s _ { 2 } = 3 \\
x _ { 1 , } x _ { 2 } , s _ { 1 } , s _ { 2 } \geq 0
\end {array} $$
گام ۲: جدول اولیه به فرم سیمپلکس تجدید نظر شده را به شکل ماتریسی مینویسیم:
$$ \large \left [ \begin {array} {ccccc}
1 & -2 & -1 & 0 & 0 \\
0 & 3 & 4 & 1 & 0 \\
0 & 6 & 1 & 0 & 1
\end {array} \right ] \left [ \begin {array} { l }
z \\
x _ { 1 } \\
x _ { 2 } \\
s _ { 1 } \\
s _ { 2 }
\end {array} \right ] = \left [ \begin {array} { c }
0 \\
6 \\
3
\end {array} \right ] $$
بردار ستونی متناظر با $$ Z $$ معمولاً با $$ e _ 1 $$ مشخص میشود. ماتریس $$ B_ 1 $$ نیز به شکل $$ { B } _ { 1 } = \left [ \beta _ { 0 } ^ { ( 1 ) } , \beta _ { 1 } ^ { ( 1 ) } , \beta _ { 2 } ^ { ( 1 ) } \ldots \beta _ { \mathrm { n } } ^ { ( 1 ) } \right ] $$ است. بنابراین، ستونهای $$ \beta _ { 0 } ^ { ( 1 ) } $$، $$\beta _ { 1 } ^ { ( 1 ) } $$ و $$\beta _ { 2 } ^ { ( 1 ) } $$ پایههای ماتریس $$ B_ 1 $$ هستند.
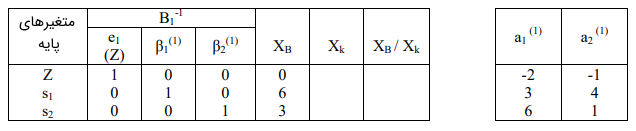
گام ۳: $$ \Delta _ j $$ برای $$ a _ 1 ^ {(1)}$$ و $$ a _ 2 ^ { (1)}$$ را محاسبه میکنیم.
$$\Delta _ 1 $$: اولین سطر $$ B_ 1 ^ {-1} \times a _ 1 ^ { ( 1 )} = 1 \times - 2 + 0 \times 3 + 0 \times 6 = - 2 $$
$$\Delta _ 2 $$: اولین سطر $$ B_ 1 ^ {-1} \times a _ 2 ^ { ( 1 )} = 1 \times - 1 + 0 \times 4 + 0 \times 1 = - 1 $$
گام ۴: آزمون بهینه بودن را اعمال میکنیم.
هر دو $$ \Delta _ 1 $$ و $$ \Delta _ 2 $$ منفی هستند. بنابراین، منفیترین مقدار را پیدا میکنیم و و بردار وارد شونده را تعیین میکنیم. منفیترین مقدار $$ \Delta _ 1 = - 2 $$ است. این مشخص میکند که $$ a _ 1 ^ {(1)} ( x _ 1 ) $$ بردار وارد شونده است.
برای آشنایی بیشتر با روش سیمپلکس، «فرادرس» اقدام به انتشار فیلم آموزش الگوریتم سیمپلکس (Simplex) در قالب یک آموزش ۱/۵ ساعته کرده که در ادامه متن به آن اشاره شده است.
- برای دیدن فیلم آموزش الگوریتم سیمپلکس (Simplex) + اینجا کلیک کنید.
گام ۵: بردار ستونی $$ X _ k $$ را محاسبه میکنیم:
$$ \large X_ k = B_ 1 ^ {-1} \times a _ 1 ^ {(1)} $$
$$ \large \left [ \begin {array} { c c c }
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end {array} \right ] \times \left [ \begin {array} { c }
- 2 \\
3 \\
6
\end {array} \right ] = \left [ \begin {array} { c }
- 2 \\
3 \\
6
\end {array} \right ] $$
گام ۶: بردار خارج شونده را تعیین میکنیم. قرار نیست برای سطر $$ Z $$ این کار را انجام دهیم.
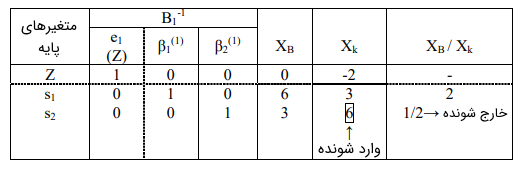
گام ۷: جواب بهبودیافته را تعیین میکنیم.
ستون $$ e _ 1 $$ هرگز تغییر نخواهد کرد و $$ x _ 1 $$ وارد شونده است، بنابراین، آن را بیرون از مرز مستطیل قرار میدهیم.
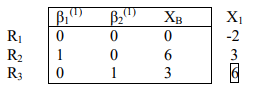
عنصر لولا را به $$ 1 $$ تبدیل میکنیم و عناصر ستون مربوطه را صفر میکنیم.

جدول را برای تکرار دوم تشکیل میدهیم.
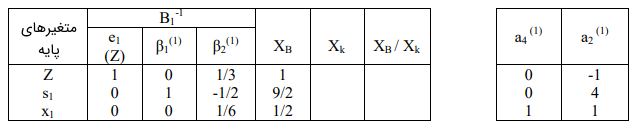
مقادیر زیر را داریم:
$$ \large \begin {array} { l }
\Delta _ { 4 } = 1 \times 0 + 0 \times 0 + 1 / 3 \times 1 = 1 / 3 \\
\Delta _ { 2 } = 1 \times - 1 + 0 \times 4 + 1 / 3 \times 1 = - 2 / 3
\end {array} $$
میبینیم که $$\Delta _ 2 $$ منفیتر است، بنابراین، $$ a _ 2 ^ {(1)}$$ بردار وارد شونده است.
اکنون بردار ستونی را محاسبه میکنیم:
$$ \large \left [ \begin {array} {ccc}
1 & 0 & 1 / 3 \\
0 & 1 & - 1 / 2 \\
0 & 0 & 1 / 6
\end {array} \right ] \times \left [ \begin {array} { c }
- 1 \\
4 \\
1
\end {array} \right ] = \left [ \begin {array} { c }
- 2 / 3 \\
7 / 2 \\
1 / 6
\end {array} \right ] $$
حال، بردار خارج شونده را تعیین میکنیم.
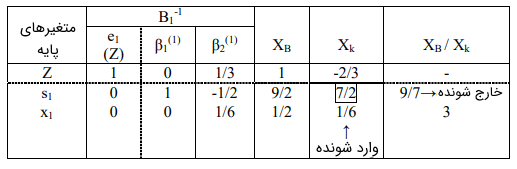
در نهایت، جواب بهبودیافته را مشخص میکنیم.
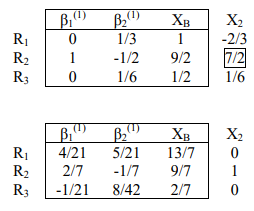
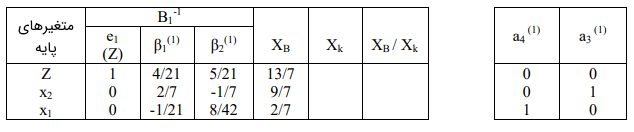
اکنون $$\Delta _ 3 $$ و $$ \Delta _ 4 $$ را محاسبه میکنیم:
$$ \large \begin {array} { l }
\Delta _ { 4 } = 1 \times 0 + 4 / 2 1 \times 0 + 5 / 2 1 \times 1 = 5 / 2 1 \\
\Delta _ { 3 } = 1 \times 0 + 4 / 2 1 \times 1 + 5 / 2 1 \times 0 = 4 / 2 1
\end {array} $$
$$ \Delta _ 4 $$ و $$ \Delta _ 3 $$ مثبت هستند. بنابراین، جواب بهینه $$ \text {Max} \; Z = 13 / 7 $$، $$x _ 1 = 2 / 7 $$ و $$ x _ 2 = 9 / 7 $$ است.
مثالی از روش سیمپلکس تجدید نظر شده
میخواهیم مسئله زیر را حل کنیم:
$$ \large \operatorname {Max} Z = x _ { 1 } + 2 x _ { 2 } \\ \large \text {Subject to} \;\;\;
\begin {array} { l }
x _ { 1 } + x _ { 2 } \leq 3 \\
x _ { 1 } + 2 x _ { 2 } \leq 5 \\
3 x _ { 1 } + x _ { 2 } \leq 6 \\
x _ { 1 } , x _ { 2 } \geq 0
\end {array} $$
حل: مسئله را به فرم زیر مینویسیم:
$$ \large \operatorname {Max} \;\;\; Z = x _ { 1 } + 2 x _ { 2 } + 0 s _ { 1 } + 0 s _ { 2 } + 0 s _ { 3 }
\\ \large \text {Subject to} \;\;\;\;
\begin {array} { l }
x _ { 1 } + x _ { 2 } + s _ { 1 } = 3 \\
x _ { 1 } + 2 x _ { 2 } + s _ { 2 } = 5 \\
3 x _ { 1 } + x _ { 2 } + s _ { 3 } = 6 \\
\text { } x _ { 1 } , x _ { 2 } , s _ { 1 } , s _ { 2 } , s _ { 3 } \geq 0
\end {array} $$
فرم استاندارد اول مسئله به شکل زیر است:
$$ \large \begin {array} { l }
Z - x _ { 1 } - 2 { x } _ { 2 } - 0 { s } _ { 1 } - 0 { s } _ { 2 } - 0 { s } _ { 3 } = 0 \\
{ x } _ { 1 } + { x } _ { 2 } + { s } _ { 1 } + 0 { s } _ { 2 } + 0 { s } _ { 3 } = 3 \\
{ x } _ { 1 } + 2 { x } _ { 2 } + 0 { s } _ { 1 } + { s } _ { 2 } + 0 { s } _ { 3 } = 5 \\
3 { x } _ { 1 } + { x } _ { 2 } + 0 { s } _ { 1 } + 0 { s } _ { 2 } + { s } _ { 3 } = 6 \\
{ x } _ { 1 } , { x } _ { 2 } , { s } _ { 1 } , { s } _ { 2 } , { s } _ { 3 } \geq 0
\end {array} $$
و به فرم ماتریسی، داریم:

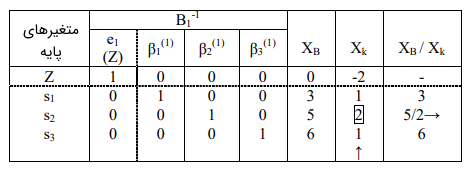
جدول سیمپلکس تجدید نظر شده نیز به شکل زیر خواهد بود.
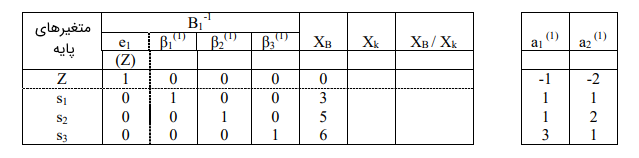
محاسبه $$ \Delta _ j $$ برای $$ a_ 1 ^ {(1)}$$ و $$ a _ 2 ^ { ( 1 ) } $$ به صورت زیر است:
$$ \Delta _ 1 $$: اولین سطر $$ { B } _ { 1 } ^ { - 1 } \times { a } _ { 1 } ^ { ( 1 ) } = 1 \times - 1 + 0 \times 1+0\times 1+0\times 3=-1 $$.
$$ \Delta _ 2 $$: اولین سطر $$ { B } _ { 1 } ^ { - 1 } \times { a } _ { 2 } ^ { ( 1 ) } = 1 \times - 2 + 0 \times 1 + 0 \times 2 + 0 \times 1 = - 2 $$
میبینیم که $$ \Delta _ 2 = - 2 $$ منفیتر است. بنابراین، $$ a _ 2 ^ { ( 1 ) } (x_ 2 ) $$ بردار وارد شونده است.
بردار ستونی $$ X _ k $$ را محاسبه میکنیم:
$$ \large X _ k = B _ 1 ^ { - 1 } \times a _ 2 ^ { ( 1 ) } $$
$$ \large \left [ \begin {array} { c c c c }
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end {array} \right ] \times \left [ \begin {array} { c }
- 2 \\
1 \\
2 \\
1
\end {array} \right ] = \left [ \begin {array} { c }
- 2 \\
1 \\
2 \\
1
\end {array} \right ] $$
اکنون جواب بهبودیافته را مشخص میکنیم.
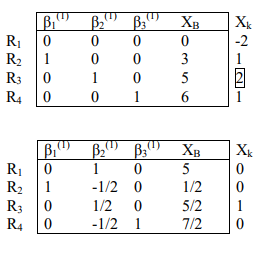
جدول سیمپلکس تجدید نظر شده برای تکرار دوم به صورت زیر است:
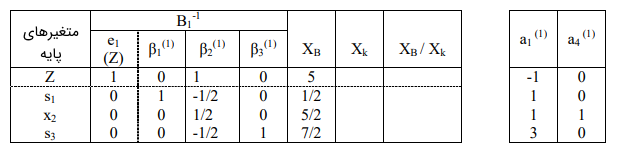
مقادیر $$ \Delta _ 1 $$ و $$ \Delta _ 4 $$ به صورت زیر محاسبه میشوند:
$$ \large \begin {array} { l }
\Delta _ { 1 } = 1 \times - 1 + 0 \times 1 + 1 \times 1 + 0 \times 3 = 0 \\
\Delta _ { 4 } = 1 \times 0 + 0 \times 0 + 1 \times 1 + 0 \times 0 = 1
\end {array} $$
میبینیم که $$ \Delta _ 1 $$ و $$ \Delta _ 4 $$ مثبت هستند. بنابراین، جواب بهینه $$ \text{Max}\; Z = 5 $$، $$ x _ 1 = 0 $$ و $$ x_ 2 = 5 / 2 $$ خواهد بود.
فیلم آموزش الگوریتم سیمپلکس (Simplex)
برای آشنایی بهتر با روش سیمپلکس، پیشنهاد میکنیم دوره ویدیویی «آموزش الگوریتم سیمپلکس (Simplex)» را مشاهده کنید. در این آموزش که مدت زمان آن ۱ ساعت و ۲۸ دقیقه است، ابتدا مقدمهای درباره روش سیمپلکس ارائه شده و پس از آن درباره شرایط حل مسئله سیمپلکس بحث شده است. سایر سرفصلهای این دوره ویدیویی عبارتند از: گامهای الگوریتم سیمپلکس، استانداردسازی مسئله، تشکیل جدول اولیه، انتخاب متغیر وارد شونده و بررسی شرایط ورود، انتخاب متغیر خارج شونده و بررسی تست مینیمم، انجام عملیات لولایی و رفتن به نقطه جدید، برسی شرایط توقف، بررسی حالات خاص، جواب بهینه نامتناهی، تباهیدگی، جواب بهینه چندگانه، جواب بهینه منحصر به فرد و بررسی روابط جدول سیمپلکس. همچنین، در پایان این آموزش، مثال جامعی حل شده است.
- برای دیدن فیلم آموزش الگوریتم سیمپلکس (Simplex) + اینجا کلیک کنید.











