حل معادله درجه اول + فرمول، مثال و حل مسئله

در آموزش‌های پیشین مجله فرادرس با معادله و مفاهیم مرتبط با آن آشنا شدیم. در این آموزش با روش‌های حل معادله درجه اول آشنا می‌شویم.

معادله درجه اول چیست؟

معادله یک گزاره ریاضی است که بیان‌کننده مساوی بودن دو عبارت است که با علامت “=” نمایش داده می‌شود. تصویر زیر یک معادله را نشان می‌دهد که اجزای آن مشخص شده‌اند.

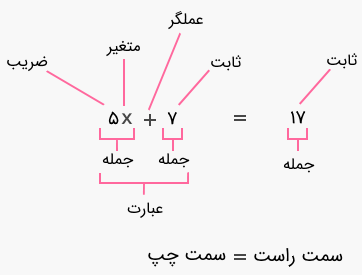
هر معادله‌ای می‌تواند شامل متغیر مجهول باشد. برای مثال، در معادله $$ x + 2 = 5$$، یک مجهول داریم و آن متغیر $$ x $$ است. بزرگ‌ترین توان مجهول را درجه معادله می‌نامند. برای مثال:

• $$x + 3 x = 4 $$ معادله درجه اول است.
• $$ x ^ 2 - x + 1 = 0 $$ معادله درجه دوم است، زیرا بزرگ‌ترین توان $$ x $$ برابر با $$2$$ است.
• $$ x ^ 8 = 1 $$ یک معادله درجه $$ 8$$ است، زیرا بزرگ‌ترین توان $$ x $$ در معادله $$ 8 $$ است.
• $$ 1 - x = x ^ 2 + 3 x $$‌ یک معادله درجه دوم است، زیرا بزرگ‌ترین توان $$ x $$ در بین جملات $$2$$ است.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

روش حل معادله درجه اول

منابع مختلف معادله درجه اول را به شکل‌های مختلفی می‌نویسند. اما در اغلب کتاب‌های درسی شکل کلی یک معادله درجه اول به‌صورت زیر بیان می‌شود:

$$ \large a x + b = 0 $$

که در آن، $$ a \neq 0 $$ است. در معادله بالا، $$ a $$ ضریب $$ x $$ و $$ b $$ عدد است.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

اما جواب این معادله چگونه به‌دست می‌آید؟ برای به دست آوردن این معادله، ابتدا با اضافه کردن $$ - b $$ به طرفین، $$ b $$ را حذف می‌کنیم:

$$ \large a x + b - b = 0 - b $$

بنابراین، معادله به‌صورت زیر درخواهد آمد:

$$ \large a x = - b $$

اکنون، برای حذف ضریب $$ a $$، دو طرف را بر $$ a $$ تقسیم می‌کنیم و جواب نهایی معادله را به‌دست می‌آوریم:‌

$$ \large x = - \frac ba $$

دقت کنید که برای استفاده از رابطه اخیر برای محاسبه جواب معادله درجه اول، باید معادله به‌فرمی باشد که آن را بیان کردیم.

چگونه یک معادله درجه اول تشکیل دهیم؟

برای تشکیل معادله درجه اول و هر معادله دیگری، ابتدا باید بدانیم مجهول چیست. معمولاً مجهول را با متغیری مثل $$ x $$ نشان می‌دهیم. برای مثال، فرض کنید می‌خواهیم عددی را بیابیم که چهار برابر آن به‌علاوه ۳ برابر با سه برابر آن منهای ۱ باشد. چه چیزی در این سؤال مجهول است؟ عدد. پس نام عدد را که مجهول است $$ x $$ یا هر حرف دیگری می‌گذاریم ($$x$$ از همه رایج‌تر است). در ادامه، سؤال را به‌صورت ریاضی می‌نویسیم.

• چهار برابر عدد به‌علاوه ۳ را این‌گونه می‌نویسیم: $$ 4 x + 3 $$.
• سه برابر عدد منهای ۱ نیز این‌گونه نوشته می‌شود: $$ 3 x - 1 $$.

این دو عبارت با هم برابر هستند و منجر به معادله زیر می‌شوند:

$$ 4 x + 3 = 3 x - 1 $$

اکنون یک معادله داریم و باید آن را به‌شکل کلی $$ a x + b = 0 $$ درآوریم. بدین منظور، $$ x $$ها و عددها را به سمت چپ می‌آوریم:

$$ \large \begin {align*} 4 x + 3 - 3 x + 1 &= 0
\\ x + 4 & = 0
\end {align*}
$$

اکنون معادله به‌فرم استاندارد درآمده و در آن، $$ a = 1 $$ و $$ b = 4 $$ است. بنابراین، جواب معادله به‌صورت زیر به‌دست می‌آید:

$$ \large x = - \frac b a = - \frac {4}{1} = - 4 $$

بنابراین، $$ x = -4 $$ است و عددی که به دنبال یافتنش بودیم $$ - 4 $$ است.

حل معادله درجه اول کسری

گاهی پیش می‌آید که اعداد موجود در معادله کسری هستند. برای مثال، معادله یک مجهولی زیر را در نظر بگیرید:‌

$$ \large - \frac 35 x + 1 = -\frac {12} {15} $$

می‌بینیم که برخی از اعداد موجود در این معادله کسری هستند. برای حل این معادله دو کار می‌توانیم انجام دهیم.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

اول اینکه می‌توانیم مانند روشی که گفتیم، معادله را به فرم استاندارد درآوریم و آن را حل کنیم. در این حالت، $$ a$$ و $$ b $$ اعدادی کسری خواهد بود. برای استفاده از این روش، باید ضرب و تقسیم کسرها را بتوانید. انجام دهید. در آموزش «تقسیم کسرها — به زبان ساده + حل تمرین و مثال» در این باره بحث کرده‌ایم.

برای مثال، می‌خواهیم، معادله‌ای را که به آن شاره کردیم، حل کنیم.

ابتدا همه اعداد معلوم و مجهول را به سمت چپ می‌آوریم تا معادله به‌‌فرم استاندارد درآید:‌

$$ \large \begin {align*} - \frac 35 x + 1 + \frac {12} {15} & = 0
\\
- \frac 35 x +\frac {27}{15} &=0
\end {align*} $$

می‌بینیم که در این معادله، $$ a = -\frac 35 $$ و $$ b = \frac {27}{15} $$ است.

بنابراین، جواب معادله به‌صورت زیر خواهد بود:

$$ \large \begin {align*} \\
x & = - \frac b a = - \frac {\frac {27}{15}}{- \frac 35} \\
& = - \frac {27}{15} \times - \frac 53 = 3
\end {align*} $$

یک راه دیگر برای حل معادله یک مجهولی یا همان درجه اول کسری این است که از همان ابتدا، کسرها را به عدد تبدیل کنیم. برای انجام این کار، باید کوچک‌ترین مضرب مشترک بین مخرج کسرها را محاسبه کرده و در دو طرف معادله ضرب کنیم. برای آشنایی با محاسبه کوچک‌ترین مضرب مشترک، به آموزش «ک م م یا کوچکترین مضرب مشترک چیست؟ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید. بار دیگر، معادله را درنظر بگیرید:

$$ \large - \frac 35 x + 1 = -\frac {12} {15} $$

ک.م.م دو عدد $$ 5 $$ و $$ 15 $$، برابر با $$ 15 $$ است. این عدد را در دو طرف معادله ضرب می‌کنیم و به‌فرم استاندارد درمی‌آوریم:

$$ \large \begin {align*}
15 \times ( - \frac 35 x + 1 ) & = 15 \times ( -\frac {12} {15}) \\
-9 x + 15 & = -12 \\
- 9 x + 15 + 12 & = 0 \\
- 9 x +27 & = 0
\end {align*} $$

می‌بینیم که معادله به‌فرم استاندارد درآمده و در آن، $$ a = -9 $$ و $$ b = 27 $$ است. بنابراین، جواب معادله به‌صورت زیر خواهد بود:

$$ \large x = - \frac ba = - \frac {2 7 }{ - 9 } = 3 $$

می‌بینیم که جواب معادله با هر دو روش یکسان به‌دست آمده است.

ما و ما و نصف ما و...

یکی از سؤال‌ها یا معماهای جالبی که در دوران مدرسه آن را شنیده‌اید یا ممکن است بشنوید، این است:‌ ما و ما نصف ما و نصفه‌ای از نصف ما، گر تو هم با ما شوی، جملگی 100 می‌شویم. سؤال این است که این ما چه تعدادی است.

ما را $$ x $$ درنظر می‌گیریم و مسئله را به‌زبان ریاضی می‌نویسیم.

• ما: $$x$$
• نصف ما: $$ \frac x 2 $$
• نصفه‌ای از نصف ما: $$ \frac x 4 $$

مسئله به‌صورت ریاضی این‌گونه خواهد بود:‌

$$ \large x + x + \frac 12 x + \frac 14 x + 1 = 100 $$

در معادله بالا، عدد $$ 1 $$ مربوط به آن بخش است که گفته شده تو هم با ما شوی. عدد $$ 100 $$ هم که مشخص است مربوط به جملگی صد است.

می‌بینیم که معادله درجه اول است و می‌توان آن را به‌صورت استاندارد نوشت:

$$ \large 2 x + \frac 12 x + \frac 14 x + 1 - 100 = 0 $$

برای حذف کردن کسرها، کوچک‌ترین مضرب مشترک آن‌ها را محاسبه کرده و در دو طرف معادله ضرب می‌کنیم. کوچک‌ترین مضرب مشترک بین $$ 2 $$ و $$ 4 $$، عدد $$ 4 $$ است. پس عدد $$ 4 $$ را در دو طرف معادله ضرب می‌کنیم:

$$ \large \begin {align*}
4 (2 x + \frac 12 x + \frac 14 x + 1 - 100) & = 4 (0)
\\ 8 x + 2 x + x + 4 - 400 & = 0 \\
11 x -396 = 0
\end {align*} $$

مشاهده می‌کنیم که معادله به‌فرم استاندارد درآمده ($$a = 11 $$ و $$ b = -396 $$) و می‌توان با فرمول جواب آن را به‌دست آورد:

$$ \large x = - \frac b a = - \frac {- 396}{11} = 36 $$

بنابراین، $$ x = 36 $$ و جواب این معما $$ 36 $$ است.

مثال‌های معادله درجه اول

در این بخش چند مثال را از معادله درجه اول حل می‌کنیم.

فیلم آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی در فرادرس

کلیک کنید

مثال اول معادله درجه اول

فرض کنید معادله زیر را داریم:

$$ \large 4 x + 2 = 10 $$

حل: باید معادله را به‌فرم $$ ax + b = 0 $$ درآوریم. برای این کار عدد سمت راست معادله، یعنی $$ 10 $$ را به سمت چپ منتقل و علامت آن را قرینه می‌کنیم. پس، معادله به‌صورت زیر درمی‌آید:

$$ \large \begin {align*}
4 x + 2 & = 10 \\
4 x + 2 -10 & = 0 \\
4 x - 8 & = 0
\end {align*} $$

می‌بینیم که معادله به همان فرمی است که بیان کردیم. در این معادله، $$ b = - 8 $$ و $$ a = 4 $$ است. بنابراین، جواب معادله برابر است با:

$$ \large x = -\frac b a = - \frac { - 8 }{4 }= 2 $$

مثال دوم معادله درجه اول

اگر جواب معادله $$ x + 3 = a x - 1 $$ برابر با $$ x = 2 $$ باشد، آنگاه مقدار $$ a $$ را به‌دست آورید.

حل: مقدار $$ x = 2 $ را در معادله جایگذاری می‌کنیم و داریم:

$$ \large  2 + 3 = a \times 2 - 1 \Rightarrow5 = 2a-1 \\
\large \Rightarrow5 + 1 = 2a \Rightarrow6 = 2 a \Rightarrow a = 3 $$

مثال سوم معادله درجه اول

محیط یک مستطیل برابر با ۲۰ واحد است. اگر طول مستطیل به‌اندازه ۴ واحد از عرضش بیشتر باشد، اندازه طول و عرض را تعیین کنید.

حل: فرض می‌کنیم عرض مستطیل برابر با $$x$$ و طول آن $$ x + 4 $$ باشد. می‌دانیم که محیط یک مستطیل دو برابر مجموع طول و عرضش است. بنابراین، خواهیم داشت:

$$ \large 2 ( x ) ( x +4) = 20 $$

اکنون باید $$ x $$ را از معادله بالا به‌دست آوریم.

$$ \large 2 ( x + x +4) = 20 \Rightarrow 2 (2x+4) = 20 \\
\large \Rightarrow2x + 4 = 10 \Rightarrow2x = 6 \\
\large \Rightarrow x = 3
$$

مقدار $$ x = 3 $$ نشان می‌دهد که عرض مستطیل برابر با ۳ واحد و طول آن ۷ واحد است.

مثال چهارم معادله درجه اول

مجموع چهار عددی متوالی $$ 30 $$ است. آن اعداد را محاسبه کنید.

حل: عدد مورد نظر را که مجهول است، برابر با $$ x $$ درنظر می‌گیریم. بنابراین، عدد بعدی می‌شود $$ x + 1 $$، بعدی $$ x + 2 $$ و آخری $$ x + 3 $$. اکنون این چهار عدد را با هم جمع می‌کنیم که حاصل جمع آن‌ها باید برابر با $$ 30 $$ باشد.

$$ \large x + (x + 1 ) + ( x + 2 ) + ( x + 3 ) = 34 $$

این معادله به‌صورت زیر ساده می‌شود:

$$ \large \begin {align*} x + x + 1 + x + 2 + x + 3 & = 30 \\
x +x +x +x +1 + 2 + 3 & = 34 \\
4 x + 6 & = 30
\end {align*} $$

اکنون معادله را به‌شکل استاندارد می‌نویسیم تا جواب آن‌ را به‌دست آوریم:

$$ \large \begin {align*}
4 x + 6 & = 30 \\
4 x + 6 - 30 & = 0 \\
4 x -24 & = 0
\end {align*} $$

در این معادله، $$ a = 4 $$ و $$ b = - 24 $$ است. جواب برابر خواهد بود با:

$$ \large x = - \frac ba = - \frac {- 2 4 } { 4 } = 6 $$

پس $$ x $$ برابر با $$ 6 $$ است. جواب نهایی سؤال این می‌شود که چهار عدد متوالی این‌ها هستند:

$$ \large 6 , 7 , 8 , 9 $$

مثال پنجم معادله درجه اول

از چهار برابر عددی سه واحد کم کرده‌ایم و حاصل برابر با 13 شده است. این عدد را حساب کنید.

حل: عدد مجهول را $$ x $$ درنظر می‌گیریم. پس، معادله‌ای به‌شکل زیر خواهیم داشت:

$$ \large 4 x -3= 13 $$

برای به‌دست آوردن $$ x $$، باید معادله را به‌فرم استاندارد بنویسیم. داریم:

$$ \large 4 x -3 -13=0 \Rightarrow 4 x - 16 = 0 $$

در این معادله، $$ a = 4 $$ و $$ b = - 16 $$ است. جواب به‌‌صورت زیر است:

$$ \large x = - \frac ba = - \frac { - 1 6 } { 4 } = 4 $$

جمع‌بندی

در این آموزش، با معادله درجه اول و روش حل معادله درجه اول آشنا شدیم. همچنین، مثال‌های متنوعی را از روش‌های تشکیل معادله درجه اول و حل آن حل کردیم.