تولید اعداد تصادفی با Mersenne Twister — الگوریتم و مفاهیم اولیه | به زبان ساده

«اعداد تصادفی» (Random Number) و همچنین اعداد «شبه تصادفی» (Pseudo Random) در صنعت، نمونهگیری و توزیعهای آماری و بخصوص در «رمزنگاری» (Cryptography) اطلاعات رایانهای کاربرد دارند. الگوریتم و روشهای مختلفی برای تولید اعداد شبه تصادفی وجود دارد که یکی از مرسوم ترین آنها روش تولید اعداد تصادفی با Mersenne Twister یا الگوریتم Mersenne Twister است. به علت پرکاربرد بودن این تکنیک در بسیاری از نرمافزارهای رایانهای، در این متن به معرفی تکنیک تولید اعداد تصادفی به روش Mersenne Twister میپردازیم. در انتها نیز دو بخش برای معرفی این الگوریتم با استفاده از شبه کد و همچنین کد پایتون اشاره خواهیم کرد.
به منظور درک بهتر از ساختار و نحوه تولید اعداد تصادفی پیشنهاد میشود که مطالب اعداد تصادفی (Random Numbers) — تاریخچه و کاربردها و توزیع یکنواخت گسسته و پیوسته — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن معرفی رمزنگاریهای رایج؛ چرا نباید شیوههای جدید رمزنگاری ابداع کرد؟ و عدد تصادفی در اکسل — راهنمای کاربردی نیز خالی از لطف نیست.
تولید اعداد تصادفی با Mersenne Twister
«مرسن پیچشی» «Mersenne Twister» یک تولید کننده «اعداد شبه تصادفی» (Pseudo Random Number Generator) یا به اختصار PRNG است. روشهای مبتنی بر PRNG بیشترین کاربرد عمومی در تولید اعداد (شبه) تصادفی را دارد. نام روش تولید اعداد تصادفی با Mersenne Twister از این واقعیت ناشی میشود که طول دوره تناوب آن به عنوان یک «عدد اول مرسن» (Mersenne prime) انتخاب شده است.
نکته: در ریاضیات، «عدد اول مرسن» (Mersenne Prime) یک عدد اول است که به فرم $$2^n-1$$ قابل نمایش است. در اینجا $$n$$ یک عدد طبیعی است. برای مثال به ازاء $$n=3$$، خواهیم داشت، $$2^3-1 = 7$$. بنابراین ۷ یک عدد اول مرسن است.
Mersenne Twister در سال 1997 توسط دو دانشمند ژاپنی به نامهای «ماکوتو ماتسومو» (Makoto Matsumoto) و «تاکوجی ناشیمورا» (Takuji Nishimura) ابداع گشت. این روش به طور خاص برای رفع بسیاری از نقایص موجود در روشهای قدیمی مولد اعداد شبه تصادفی طراحی شده است.
متداولترین نسخه الگوریتم Mersenne Twister براساس Mersenne prime 219937−1 ساخته شده است. در اجرای نسخه استاندارد آن، یعنی MT19937، از کلمه با طول 32 بیت استفاده میشود. پیاده سازی دیگری نیز وجود دارد که از کلمه با طول 64 بیت، MT19937-64 استفاده میکند. این الگوریتم توالی متفاوتی نسبت به الگوریتم ۳۲ بیتی ایجاد میکند. عبارت MT مخفف Mersenne Twister است. به همین دلیل در ادامه متن هرگاه بخواهیم به مرسن پیچشی اشاره کنیم از خلاصه آن یعنی MT بهره میگیریم.
کاربرد در سیستمهای نرم افزاری
روش «مولد اعداد شبه تصادفی» (Mersenne Twister PRNG) به منظور تولید اعداد تصادفی در نرم افزارهای متعددی به عنوان پیشفرض قرار گرفته است. در این بین میتوان به اکسل مایکروسافت (Microsoft Excel)، Dyalog APL، GAUSS, GLIB، GNU Octave و کتابخانه علمی گنو ( GNU Scientific Library)، جولیا (Julia) و همچنین نرم افزارهای متلب (Matlab)، میپل (Maple) اشاره کرد. در ضمن در زبانهای برنامهنویسی R، پایتون (Python) و همچنین روبی (Ruby) از این روش برای تولید اعداد تصادفی استفاده میشود.
همچنین MT PRNG در Apache Commons، در ++C استاندارد (از C ++ 11) و Mathematica نیز موجود است. پیاده سازی این الگوریتم در بسیاری از کتابخانههای برنامهها از جمله Boost C ++ Libraries، کتابخانه CUDA، و کتابخانه عددی NAG ارائه شده است.
مرسن پیچشی، یکی از دو دو روش تولید اعداد تصادفی در نرمافزار SPSS نیز هست. در حقیقت روش دیگر در این نرمافزار به منظور سازگاری با برنامههای قدیمی نگه داشته شده ولی به هر حال Mersenne Twister قابل اطمینانتر است. Mersenne Twister نیز به همین ترتیب یکی از PRNGها در SAS است. این روش به طور پیشفرض در نرمافزار Stata نیز قرار دارد. روش KISS یا (Keep it Simple Stupid) به معنی ساده نگهداشتن، به منظور هماهنگی با نسخههای قدیمی هنوز در Stata موجود است.
همه مولدهای اعداد تصادفی خانواده KISS سه یا چهار مولد اعداد تصادفی مستقل را با هدف بهبود کیفیت تصادفی ترکیب میکنند. مولد اعداد تصادفی KISS در نسخه اصلی که در 1993 معرفی شد، بر اساس ترکیبی از یک «مولد همگام خطی» (linear congruential generator) و دو مولد «ثبات تغییر بازخورد خطی» (Linear-feedback shift register) یا LFSR عمل میکرد.
نکته: سادهترین شیوه تولید اعداد تصادفی به صورت مولد همگام خطی یا LCG است که به صورت زیر عمل میکند.
$$ \large X_{n+1} = (aX_n + b)\; mod(m)$$
رابطه اخیر، نشانگر همنهشت بودن دنباله اعداد تصادفی به پیمانه $$m$$ با فرض ثابت بودن $$a$$ و $$b$$ است.
مزایا
روش تولید اعداد شبه تصادفی MT، دارای مجوز آزاد (Permissively-licensed) بوده و بدون حق ثبت اختراع برای همه انواع قابل استفاده است. البته نسخه CryptMT این خاصیت را ندارد.
الگوریتم MT، در آزمونهای بیشمار و متعدد آماری برای نمایش تصادفی بودن را با موفقت پشتسر گذاشته است. از جمله آزمونها میتوان به «تست دایهارد» (Diehard Test) اشاره کرد. البته توجه داشته باشید که MT در همه آزمونهای TestU01 موفق نبوده است.
نکته: آزمونهای TestU01 یک کتابخانه نرم افزاری است که به زبان ANSI C پیاده سازی شده و مجموعهای از برنامههای کاربردی را برای آزمایش تصادفی بودن مولدهای اعداد تصادفی (RNG) ارائه میدهد. این کتابخانه برای اولین بار در سال 2007 توسط «پیر لسیر» (Pierre L’Ecuyer) و «ریچارد سیمارد» (Richard Simard) در دانشگاه مونترال معرفی شد.
در روشی که توسط MT پیاده سازی میشود، دوره تناوب یا تکرار اعداد تصادفی بسیار طولانی است به طوری که این دوره تناوب برابر با ۱-219937 است. البته توجه داشته باشید که نمیتوان طولانی بودن این دوره تناوب را تضمینی برای کیفیت اعداد تصادفی تولید شده دانست. اما دورههای تناوب کوتاه مدت مانند 232 که در اکثر بستههای نرم افزاری قدیمی استفاده میشوند، میتواند مشکل ساز شده و کیفیت اعداد تصادفی تولید شده را کاهش دهند.
روش تولید اعداد تصادفی با Mersenne Twister براساس توزیع k و دقت ۳۲ بیتی، دارای خصوصیات خوب و مناسبی برای $$1 \leq k \leq 623$$ است. پیاده سازیها صورت گرفته برای تولید اعداد شبه تصادفی معمولاً اعداد تصادفی را سریعتر از روشهای تصادفی واقعی (فیزیکی) ایجاد میکنند. یک مطالعه نشان میدهد که الگوریتم Mersenne Twister اعداد تصادفی ممیز شناور 64 بیتی را تقریباً بیست برابر سریعتر از مجموعه دستورالعمل RDRAND یا (Read Random) مبتنی بر سخت افزار ایجاد میکند.
معایب
برای استفاده از روش MT بافر حالت نسبتاً بزرگ است. به طوری که به 2٫5 کیلوبایت حافظه نیاز دارد. البته نسخه دیگری از آن به نام TinyMT که در ادامه مورد اشاره قرار گرفته، میزان استفاده از حافظه را بهینه کرده و با حافظه کمتری قابل استفاده است. همچنین الگوریتم MT، توان متوسط یا ضعیفی براساس استانداردهای مدرن امروزی برخوردار است، مگر اینکه از نوع SFMT استفاده شود. این تکنیک در ادامه متن معرفی شده است.
در مجموعه آزمون TestU01 دو شکست واضح در Crush و BigCrush (دو آزمون پیچیدگی خطی- Linear Complexity) وجود دارد. این آزمون، مانند مرسن توئیستر، بر اساس جبر F2 عمل میکند. البته تعدادی مولدهای دیگر برای تولید اعداد شبه تصادفی (PRGN) وجود دارد که از عهده همه آزمایشات بر میآیند.
در تولید اعداد تصادفی با Mersenne Twister موارد متعددی وجود دارد که تولید اعداد تصادفی فقط از نظر مقدار دانه (Seed) متفاوت هستند ولی سایر پارامترها با هم تفاوت ندارند به این ترتیب ممکن است مولد MT منجر به تولید اعداد تصادفی یکسانی شود. به طور کلی برای شبیه سازیهای مونت کارلو که به مولد عدد تصادفی مستقل نیاز دارند، الگوریتم MT مناسب نیست. البته توجه داشته باشید که برای انتخاب مجموعههای مختلف مقادیر پارامتر، روشهایی وجود دارد.
اگر وضعیت اولیه کاملاً تصادفی نباشد، به خصوص اگر حالت اولیه صفرهای زیادی داشته باشد، لازم است برای تولید خروجی که از آزمونهای تصادفی عبور کند، زمان زیادی صرف کرد. نتیجه این امر آن است که دو نمونه از مولد که با حالتهای اولیه تقریباً یکسان شروع شدهاند، برای بسیاری از تکرارها، توالی تقریباً یکسانی را تولید میکنند به روزرسانی سال 2002 الگوریتم تولید اعداد تصادفی با Mersenne Twister، مقدار اولیه را بهبود بخشیده است، بنابراین شروع با چنین وضعیتی بسیار بعید است. گفته میشود نسخه مخصوص پردازشگرهای گرافیکی (GPU) که MTGP نامید میشود، دارای عملکرد به مراتب بهتری است.
توجه داشته باشید که تولید اعداد تصادفی با Mersenne Twister از نظر رمزنگاری ایمن نیست، مگر اینکه از نوع CryptMT که در ادامه مورد بحث قرار گرفته، استفاده شود. دلیل این امر آن است که مشاهده تعداد تکرار کافی (که در الگوریتم MT19937 برابر با 624 است زیر اندازه بردار حالتی که از آن تکرارهای بعدی تولید میشوند را مشخص میکند) به شما امکان میدهد تمام تکرارهای آینده را پیش بینی کنید.

جایگزینهایی برای تولید اعداد تصادفی با Mersenne Twister
همانطور که میدانید، روشهای متعددی برای ایجاد اعداد (شبه) تصادفی وجود دارد. یک مولد جایگزین برای تولید اعداد تصادفی با Mersenne Twister روش توزیع مناسب با توالی طولانی خطی (Well Equidistributed Long-Period Linear) یا به اختصار WELL است که بازیابی سریعتر و تصادفی برابر با MT را ارائه کرده و از سرعت تقریباً یکسانی برخوردار است.
مولد اعداد تصادفی xorshift که توسط «مارسگلیا» (Marsaglia) معرفی شد و نسخههای مختلف آن، سریعترین در کلاس «ثبات تبدیل بازخورد خطی» (Linear feedback shift register) یا به اختصار LFSRها هستند.
MELGهای 64 بیتی یا «مولدهای 64 بیتی حداکثر تقسیم شده F2-Linear با دوره تناوب عدد اول مرسن» (64bit Maximally Equidistributed F2-Linear Generators with Mersenne Prime Period) از نظر خصوصیات توزیع k (توزیع یکنواخت-Uniform Distribution) کاملاً بهینه شدهاند.
خانواده ACORN یا عدد «تصادفی همگام جمعی» (Additive Congruential Random Number) که در سال ۱۹۸۹ منتشر شدهاند، یکی دیگر از روشهای تولید اعداد شبه تصادفی با توزیع k (توزیع یکنواخت با پارامتر k) هستند که سرعت محاسباتی آنها مشابه MT بوده ولی ویژگیهای آماری بهتری را نشان میدهند، زیرا تمام معیارهای امروزی (2019) TestU01 را برآورده میکنند. در صورت استفاده از پارامترهای مناسب، ACORN میتواند دوره تناوب دلخواه و دقت بالایی داشته باشد.
خانواده «مولدهای اعداد شبه تصادفی جایگشت همگام» (Permuted Congruential Generator) یا به اختصار PCG با استفاده از روشهای تجزیه و تحلیل مدرن، تولیدکننده دوره طولانیتر از تناوب داشته و دارای مکان حافظه پنهان بهتر و اریبی کمتر و قابل تشخیص هستند.
توزیع k
یک توالی شبه تصادفی (مثل $$x_i$$ها) از اعداد صحیح w-bit با دوره تناوب P را دارای توزیع $$k$$ با دقت $$v-bit$$ گویند اگر رابطه زیر برقرار باشد.
$$ \large {\displaystyle ({\text{trunc}}_{v} (x_ {i}) , \, {\text{trunc}}_ {v} (x_{i + 1}) , \quad \ldots ,\quad {\text{trunc}}_ {v} (x_{i + k-1})) \quad (0 \leq i <P)} $$
فرض کنید در رابطه بالا، $$trunc_{v}(x)$$، عدد تشکیل شده توسط بیتهای پیشرو x را نشان دهد، همچنین P را $$k$$ بردار $$v$$ بیتی در نظر بگیرید. در نتیجه هر یک از ترکیبات بیتها از کل ترکیبهای 2kv بیتی، به تعداد برابر در یک دوره تناوب وجود خواهند داشت. البته ترکیب صفر یکبار کمتر رخ میدهد.
جزئیات الگوریتمی
تولید اعداد تصادفی با Mersenne Twister براساس یک کلمه $$w$$ بیتی، یک عدد تصادفی از مجموعه اعداد صحیح در بازه $$[0, 2^w -1]$$ تولید میکند. تولید اعداد تصادفی با Mersenne Twister مبتنی بر یک «ماتریس با رابطه بازگشتی خطی» (Matrix Linear Recurrence) روی یک «میدان دودویی F2 متناهی» (finite binary field F2) است.
این الگوریتم یک «ثبات جابجایی بازخورد تعمیم یافته پیچیشی» ( Twisted Generalized Feedback Shift Register) یا به اختصار TGFSR است که با نمایش «بیت حالت» (State bit) و «فرم منطقی نرمال» (Rational Normal Form) ماتریس یا «فرم فربنیوس» (Frobenius normal form) عمل میکند. در این حالت ثبات را به اختصار به شکل TGFSR(R) نشان میدهند.
نکته: در فرم فربنیوس، یک فضای برداری به زیرفضاهایی چرخشی از ماتریس $$A$$ تجزیه و تفکیک میشود.
ایده اصلی این است که یک سری یا دنباله از $${\displaystyle x_{i}}$$ را به وسیله یک رابطه تکراری ساده تعریف کرده و سپس اعدادی به شکل $$ {\displaystyle x_{i} T} $$، را استخراج کرد. البته مشخص است که $${ \displaystyle T} $$ یک ماتریس F2 معکوسپذیر بوده که معمولا از آن به عنوان «ماتریس تعدیل» (Tempering Matrix) نام میبرند.
الگوریتم عمومی برای تولید اعداد تصادفی با Mersenne Twister با مقادیر زیر مشخص میشود. البته توجه داشته باشید که برخی از این توضیحات فقط پس از خواندن کل الگوریتم معنی خواهد داشت. پس همه الگوریتم را بخوانید.
- w: اندازه کلمه (به تعداد بیت).
- n: درجه بازگشت.
- m: کلمه میانی، پارامتری که در رابطه بازگشتی به کار رفته و برای تعریف دنباله $$X$$ها لازم است ($$1 \leq m <n$$).
- r: نقطه جداسازی یک کلمه یا تعداد bitmask پایینی ($$ 0 \leq r \leq w-1$$).
- a: ضرایب ماتریس پیچشی منطقی نرمال.
- b ،c: تعدیل کننده (bitmask).
- s ،t: تعدیل کننده بیت جابجایی (bit Shifts).
- u ،d ،l: بیتهای جابجایی و ماسکهای تعدیل کننده Mersenne Twister.
اول از همه به یاد داشته باشید که که 2nw - r - 1 یک عدد اول مرسن است. این انتخاب، آزمون ابتدایی و آزمون توزیع k را که برای جستجوی پارامتر مورد نیاز لازم است، ساده میکند.
دنباله $$x$$ها به عنوان مجموعهای از مقادیر $$w$$بیتی با رابطه بازگشتی زیر تعریف میشود.
$$ \large {\displaystyle x_{k + n}: = x_{k + m} \oplus \left(({x_ {k}} ^ {u} \mid \mid {x_ {k + 1}} ^ {l}) A \right) \qquad \qquad k = 0,1, \ldots} $$
که در آن $${\displaystyle \mid \mid}$$ نشانگر الحاق بردارهای بیتی (با بیتهای بالا در سمت چپ)، $${\displaystyle \oplus}$$ عملگر بیتی «یای انحصاری-Exclusive Or» یا (XOR)، $${\displaystyle {x_ {k}} ^ {u}}$$ به معنای $$w-r$$ بیت بالایی از $$x_k$$ و $${\displaystyle x^l_{k+1}} $$ نیز $$r$$ بیت پایین برای $$x_{k+1}$$ است.
در این حالت تبدیل پیچشی ماتریس $$A$$ به فرم منطقی نرمال به صورت زیر خواهد بود.
$$ \large {\displaystyle A = {\begin {pmatrix} 0 & I_{w-1} \\ a_{w- 1} &(a_{w- 2}, \ldots ,a_{0}) \end{pmatrix} }} $$
در رابطه بالا $$I_{n-1}$$ یک ماتریس همانی (مربعی با $$n-1$$ سطر و ستون) است. استفاده از فرم منطقی نرمال برای ماتریس $$A$$ این مزیت را دارد که میتوان ضرب را به صورت زیر نشان داد. البته $$x_0$$ پایینترین بیت رتبه $$x$$ است که برای نمایش آن به کار میرود.
$$ \large {\boldsymbol {x}} A= {\begin{cases}{ \boldsymbol {x}} \gg 1 & x_{0} =0 \\ ({\boldsymbol {x}} \gg 1) \oplus {\boldsymbol {a}} & x_{0} =1 \end{cases}} $$
نکته: به یاد داشته باشید که در اینجا ضرب ماتریسی در جبر F2 روی میدهد و در نتیجه عملگر بیتی XOR به عنوان جمع به کار میرود.
مانند TGFSR(R)، مرسن توئیستر با مراحل پشت سر هم و آبشاری برای جبران کاهش ابعاد توزیع یکنواخت عمل میکند. توجه داشته باشید که این امر معادل استفاده از ماتریس $$A$$ به شکل $$A = T^{-1}AT$$ است که در آن $$T$$ یک ماتریس معکوسپذیر بوده و در نتیجه مشخصههای تحلیل چند جملهای زیر برقرار است.
مانند A، تبدیل تعدیلگر را به شکلی انتخاب میکنیم که محاسبات به سادگی قابل انجام باشند. بنابراین در واقع T را نمیسازیم. این تعدیل در الگوریتم MT به صورت تعریف شده است.
$$ \large y := x \oplus ((x \gg u)\; \&\; d) $$
$$ \large y := y \oplus ((y \ll s)\; \&\; b) $$
$$ \large y := y \oplus ((y \ll t)\; \&\; c) $$
$$\large z := y \oplus (y \gg l) $$
که در آن x مقدار بعدی از دنباله اعداد است، y یک مقدار اولیه موقتی، z مقدار محاسبه شده از الگوریتم و همچنین علامتهای $$\ll$$ و $$\gg$$ نیز حرکت به سمت چپ و راست بیتها است. همچنین علامت & نیز همان «عملگر عطفی» (و منطقی- AND) برای بیتها در نظر گرفته شده است.
اولین و آخرین تبدیل به این علت آورده شدهاند که بتوانند توزیع یکنواخت برای بیت پایین را فراهم کنند. براساس خواصی که در TGFSR داریم، شرط زیر به منظور رسیدن به توزیع یکنواخت برای بیت بالایی مورد نیاز است.
$$ \large s + t \geq \lfloor w/2 \rfloor -1 $$
منظور از $$\lfloor \; \rfloor$$ جزء صحیح عدد است. در الگوریتم اولیه یا همان MT19937، ضرایب یا پارامترها به صورت زیر هستند.
- $$(w, n, m, r) = (32, 624, 397, 31)$$.
- $$a = 9908B0DF_{16} $$ (عدد برمبنای ۱۶).
- $$(u , d) = (11, FFFFFFFF_{16})$$.
- $$(s ,b) = (7, 9D2C5680_{16})$$.
- $$(t , c) = (15, EFC60000_{16})$$.
- $$l = 18$$.
توجه داشته باشید که پیاده سازی 32 بیتی Mersenne Twister معمولاً دارای $$d = FFFFFFFF_{16}$$ است. در نتیجه در اغلب موارد مقدار $$d$$ را به عنوان پارامتر در الگوریتم حذف میکنند. مشخص است که ترکیب عطفی (AND) مقدار $$d$$ با عدد دیگر به صورت بیتی، تاثیری در تغییر عدد نخواهد گذاشت.
ضرایب یا پارامترهای MT19937-64 یعنی نسخه ۶۴ بیتی برای تولید اعداد تصادفی با Mersenne Twister در ادامه دیده میشوند.
- $$(w , n , m ,r) = (64, 312, 156, 31)$$
- $$a = B5026F5AA96629E9_{16} $$ (اندیس پایین به معنی عدد برمبنای ۱۶ است).
- $$(u , d) = (29, 5555555555555555_{16})$$
- $$(s , b) = (17, 71D67FFFEDA60000_{16})$$
- $$(t , c) = (37, FFF7EEE000000000_{16})$$
- $$l = 43$$
مقداردهی اولیه
ساختار مورد نیاز برای پیاده سازی Mersenne Twister آرایهای از n مقدار است که هر کدام $$w$$ بیتی هستند. برای مقداردهی اولیه آرایه، از مقدار دانه w-bit برای مشخص کردن $$x_0$$ تا $$x_{n-1}$$ استفاده میشود. مقدار $$x_0$$ همان دانه (seed) بوده و مقادیر بعدی دنباله تصادفی به صورت زیر حاصل میشوند.
$$ \large x_i = f \times \bigl( x_{i−1} \oplus \left( x_{i−1} \gg (w−2) \right) \bigr) + i $$
مقدار $$i$$ از ۱ تا $$n-1$$ تغییر میکند. به این ترتیب اولین مقداری که الگوریتم به عنوان عدد تصادفی ایجاد میکند بستگی به $$x_n$$ داشته و وابسته به $$x_0$$ نیست. مقدار ثابت $$f$$ نیز بستگی به مولد دارد بنابراین در الگوریتم دیده نمیشود. در MT19937 مقدار آن برابر با 1812433253 و در MT19937-64 نیز برابر با 6364136223846793005 خواهد بود.
مقایسه تولید اعداد تصادفی با Mersenne Twister و GFSR کلاسیک
برای رسیدن به حد بالایی نظری 2nw - r - 1 که کران بالا در دوره تناوب TGFSR است، تابع $$\phi_B (t)$$ باید به صورت زیر باشد.
$$ \large {\displaystyle B = {\begin{pmatrix} 0& I_{w}& \cdots & 0& 0\\ \vdots & & & & \\ I_{w} & \vdots & \ddots & \vdots & \vdots \\ \vdots & & & & \\ 0& 0 & \cdots & I_{w} & 0\\ 0& 0 & \cdots & 0 & I_{w-r}\\ S & 0 & \cdots & 0 & 0 \end{pmatrix}} {\begin{matrix}\\ \\ \leftarrow m{ \hbox{-th row}}\\ \\ \\ \\ \end{matrix}}}$$
$$ \large S={\begin{pmatrix}0 & I_{r}\\ I_{w-r} &0 \end{pmatrix}}A$$
به این ترتیب روش تولید اعداد تصادفی با Mersenne Twister الگوی تولید اعداد تصادفی به کمک GFSR کلاسیک را در زمینههای زیر بهبود میبخشد.
- دوره تناوب از لحاظ نظری به حد بالایی 2nw - r - 1 میرسد.
- توزیع یکنواخت در n بُعد حاصل میشود. توجه داشته باشید روشهای دیگر مثال مولدهای همگام خطی، در بهترین حالت میتوانند توزیعی قابل قبول در پنج بُعد ایجاد کنند.
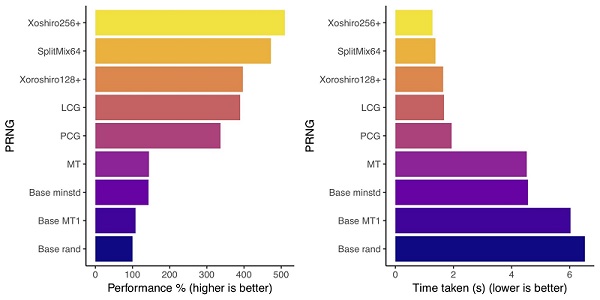
به منظور مقایسه کارایی و سرعت تولید و کیفیت اعداد ساخته شده در روش تولید اعداد تصادفی با Mersenne Twister با روشهای دیگر PRNG به نمودار بالا توجه کنید. همچنین به منظور دسترسی به برنامههای تولید اعداد تصادفی به روشهای مختلف بهتر است روی (+) کلیک کنید. برنامههایی با کد C برای پیادهسازی این الگوریتمها در لینک گفته شده، قابل مشاهده است.
شبه کد
شبه کد زیر الگوریتم عمومی Mersenne Twister را پیادهسازی کرده است. ثابتهای به کار رفته یعنی w ،n ،m ،r ،a ،u ،d ،s ،b ،t ،c ،l و f مانند توضیحات الگوریتم بالا عمل کردهاند. فرض بر این است که int یک نوع داده یا ساختار مناسب برای برای نگه داشتن مقادیر با w بیت را مشخص کرده.
1 // Create a length n array to store the state of the generator
2 int[0..n-1] MT
3 int index := n+1
4 const int lower_mask = (1 << r) - 1 // That is, the binary number of r 1's
5 const int upper_mask = lowest w bits of (not lower_mask)
6
7 // Initialize the generator from a seed
8 function seed_mt(int seed) {
9 index := n
10 MT[0] := seed
11 for i from 1 to (n - 1) { // loop over each element
12 MT[i] := lowest w bits of (f * (MT[i-1] xor (MT[i-1] >> (w-2))) + i)
13 }
14 }
15
16 // Extract a tempered value based on MT[index]
17 // calling twist() every n numbers
18 function extract_number() {
19 if index >= n {
20 if index > n {
21 error "Generator was never seeded"
22 // Alternatively, seed with constant value; 5489 is used in reference C code[53]
23 }
24 twist()
25 }
26
27 int y := MT[index]
28 y := y xor ((y >> u) and d)
29 y := y xor ((y << s) and b)
30 y := y xor ((y << t) and c)
31 y := y xor (y >> l)
32
33 index := index + 1
34 return lowest w bits of (y)
35 }
36
37 // Generate the next n values from the series x_i
38 function twist() {
39 for i from 0 to (n-1) {
40 int x := (MT[i] and upper_mask)
41 + (MT[(i+1) mod n] and lower_mask)
42 int xA := x >> 1
43 if (x mod 2) != 0 { // lowest bit of x is 1
44 xA := xA xor a
45 }
46 MT[i] := MT[(i + m) mod n] xor xA
47 }
48 index := 0
49 }در تصویر زیر روال تولید اعداد تصادفی با Mersenne Twister در حالت ۳۲ بیتی نشان داده شده. بخش مربوط به عدد استخراج شده (Extract Number) یک مثال از حالتی است که رقم صحیح ۰ به عنوان خروجی تولید شده و اندیس (Index) در رقم صحبح ۱ قرار گرفته است. زمانی که همه ارقام در خروجی قرار گیرند، روال Generate Numbers به مانند تصویر زیر، اجرا میشود.
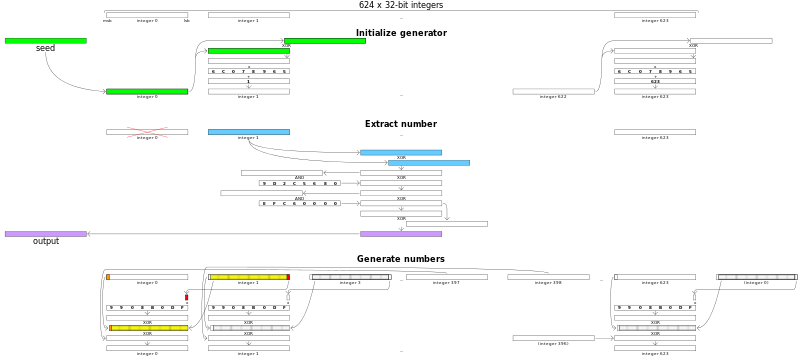
در قطعه کد زیر پیاده سازی عددی الگوریتم یا روش تولید اعداد تصادفی با Mersenne Twister در Python 3 قابل مشاهده است. واضح است که این برنامه از عدد اول مرسن به فرم ۱-231 استفاده میکند. این برنامه از دو متغیر عمومی (Global) برای تولید اعداد ممیز شناور و عدد صحیح، یا آرایههای هر دو بهره برده است.
1from warnings import warn
2
3
4class Mersenne:
5 """Pseudorandom number generator"""
6
7 def __init__(self, seed=1234):
8 """
9 Initialize pseudorandom number generator. Accepts an
10 integer or floating-point seed, which is used in
11 conjunction with an integer multiplier, k, and the
12 Mersenne prime, j, to "twist" pseudorandom numbers out
13 of the latter. This member also initializes the order
14 of the generator's period, so that members floating and
15 integer can emit a warning when generation is about to
16 cycle and thus become not so pseudorandom.
17 """
18 self.seed = seed
19 self.j = 2 ** 31 - 1
20 self.k = 16807
21 self.period = 2 ** 30
22
23 def floating(self, interval=None, count=1):
24 """
25 Return a pseudorandom float. Default is one floating-
26 point number between zero and one. Pass in a tuple or
27 list, (a,b), to return a floating-point number on
28 [a,b]. If count is 1, a single number is returned,
29 otherwise a list of numbers is returned.
30 """
31 results = []
32 for i in range(count):
33 self.seed = (self.k * self.seed) % self.j
34 if interval is not None:
35 results.append(
36 (interval[1] - interval[0]) * (self.seed / self.j) + interval[0]
37 )
38 else:
39 results.append(self.seed / self.j)
40 self.period -= 1
41 if self.period == 0:
42 warn("Pseudorandom period nearing!!", category=ResourceWarning)
43 self.period = 2 ** 30 # reset period
44 if count == 1:
45 return results.pop()
46 else:
47 return results
48
49 def integer(self, interval=None, count=1):
50 """
51 Return a pseudorandom integer. Default is one integer
52 number in {0,1}. Pass in a tuple or list, (a,b), to
53 return an integer number on [a,b]. If count is 1, a
54 single number is returned, otherwise a list of numbers
55 is returned.
56 """
57 results = []
58 for i in range(count):
59 self.seed = (self.k * self.seed) % self.j
60 if interval is not None:
61 results.append(
62 int(
63 (interval[1] - interval[0] + 1) * (self.seed / self.j)
64 + interval[0]
65 )
66 )
67 else:
68 result = self.seed / self.j
69 if result < 0.50:
70 results.append(0)
71 else:
72 results.append(1)
73 self.period -= 1
74 if self.period == 0:
75 warn("Pseudorandom period nearing!!", category = ResourceWarning)
76 self.period = 2 ** 30 # reset period
77 if count == 1:
78 return results.pop()
79 else:
80 return resultsبرای دسترسی به کدهای اصلی روش MT به زبان C میتوانید به سایت معرفی شده در (+) یا اینجا مراجعه کنید. در قسمت بعدی تکنیکهای دیگری را مورد بررسی قرار میدهیم که مبنای آنها MT بوده ولی به گونهای دیگر تولید اعداد تصادفی را اجرا میکنند.

انواع و گونههای مختلف الگوریتم Mersenne Twister
پس از آنکه الگوریتم Mersenne Twister معرفی شد، گونههای دیگری از آن نیز توسط دانشمندان دیگر مورد بررسی قرار گرفته و معایب MT را پوشش دادند. در ادامه به چهار نوع مختلف از مرسن پیچشی اشاره میکنیم که در بخشی از الگوریتم اصلی، بهبود بوجود آوردهاند.
الگوریتم CryptMT
الگوریتم CryptMT یک رمزگذار جریان و مولد اعداد شبه تصادفی با رمزنگاری امن است که از مرسن توئیستر به صورت داخلی استفاده می کند. این تکنیک توسط «ماتسوموتو» (Matsumoto) و «نیشیمورا» (Nishimura) با همکاری «ماریکو هاگیتا» ( Mariko Hagita) و موتسو سایتو (Mutsuo Saito) ساخته شد. روش CryptMT به پروژه eSTREAM و به سفارش شبکه eCRYPT اختصاص دارد. برخلاف Mersenne Twister یا سایر مشتقات آن، CryptMT دارای قوانین ثبت اختراع بوده و امکان استفاده آزاد را ندارد.
الگوریتم MTGP
الگوریتم MTGP یکی از انواع Mersenne Twister است که برای واحدهای پردازش گرافیکی منتشر شده و توسط «ماتسو سایتو» (Mutsuo Saito) و «ماکوتو ماتسومو» (Makoto Matsumoto) بهینه شده است. «عملیات بازگشتی خطی پایه» (basic linear recurrence operations) از MT گسترش یافته و پارامترها انتخاب میشوند تا به بسیاری از رشتهها، امکان محاسبه بازگشتی به صورت موازی داده شود، از طرفی در MTGP فضای حالت برای کاهش بار حافظه به اشتراک گذاشته میشود. در مقالهای ادعا میشود که MTGP نسبت به MT عملکرد بسیار بهتری حتی در پردازندههای گرافیکی (Graphical Processing Unit) قدیمی (Nvidia GTX260 با 192 هسته) دارد بطوری که فقط در 4٫7 میلیثانیه برای 10۷ × 5 عدد صحیح 32 بیتی (اعداد تصادفی) زمان صرف شده است.
الگوریتم SFMT
الگوریتم SMFT یا «پردازش موازی با یک دستور و چند داده» (SIMD Fast Mersenne Twister) یک روش برای پیادهسازی تکنیک Mersenne Twister است، که در سال 2006 معرفی شد. SMFT طوری طراحی شده است که در SIMD 128-bit، بیشترین کارایی را دارد.
نکته: عبارت SIMD، مخفف Single instruction, multiple data بوده که روشی برای اجرای «پردازش موازی» (Parallel Processing) است.
الگوریتم SFMT تقریباً دو برابر سریعتر از Mersenne Twister است. همچنین ویژگی توزیع یکنواخت (Equidistributed) در الگوریتم SFMT بهتر از MT است. از طرفی از تناوبهای مختلف از ۱-2607 تا ۱-2216091 را پشتیبانی میکند.
پردازشگرهای اینتل سری SSE2 و همچنین Power PC AltiVec که قادر به پردازش موازی هستند از الگوریتم SFMT بهره میبرند. همچنین در کنسولهای بازی نیز باید به Cell BE در PlayStation 3 اشاره داشت که روش تولید اعداد تصادفی در آنها براساس این الگوریتم صورت گرفته است.
الگوریتم TinyMT
الگوریتم TinyMT یکی از انواع روشهای تولید اعداد تصادفی با Mersenne Twister است که توسط سایتو و ماتسوموتو در سال 2011 پیشنهاد شده است. TinyMT فقط از 127 بیت فضای حالت استفاده میکند که در مقایسه با حالت 2٫5 کیلوبایتی اصلی، کاهش قابل توجهی دارد. با این حال، دوره تناوب آن 1-2127 است که به مراتب کوتاهتر از دوره اصلی در MT است. بنابراین فقط در مواردی که حافظه دارای هزینه بالایی است، استفاده از آن توصیه میشود.
خلاصه و جمعبندی
در این نوشتار الگوریتم و شیوه تولید اعداد تصادفی به کمک تکنیک «مرسن تویستر» (Mersenne Twister) به عنوان یکی از تکنیکهای تولید اعداد شبه تصادفی را فرا گرفتیم. قابلیت اطمینان و سرعت تولید اعداد تصادفی در روش تولید اعداد تصادفی با Mersenne Twister باعث شده است که از آن در بسیاری از نرمافزارها و سختافزاری امروزی استفاده شود. از این جهت در این متن از مجله فرادرس به این موضوع پرداخته و ویژگیهای این روش تولید اعداد شبیه تصادفی آشنا شدیم.










