تابع تبدیل پالسی — از صفر تا صد

در آموزش‌های پیشین مجله فرادرس، با نمایش تابع تبدیل سیستم‌های پیوسته در زمان بحث کردیم. در این آموزش با تابع تبدیل پالسی آشنا می‌شویم که در سیستم‌های گسسته در زمان کاربرد دارد.

همان‌طور که می‌دانیم، تابع تبدیل یک سیستم LTI (خطی تغییرناپذیر با جریان) پیوسته در زمان به صورت زیر تعریف می‌شود:

$$ \large
G ( s ) = \frac { C ( s ) } { R ( s ) }
$$

که در آن، $$ R ( s ) $$ و $$ C ( s ) $$، به ترتیب، تبدیل لاپلاس‌های ورودی $$ r ( t) $$ و خروجی $$ c ( t ) $$ هستند. فرض می‌کنیم شرایط اولیه صفر است.

تابع تبدیل پالسی سیستم حلقه‌باز

تابع تبدیل پالسی (Pulse Transfer Function) با نسبت تبدیل z خروجی در لحظات نمونه‌برداری به تبدیل z ورودی نمونه‌برداری شده تعریف می‌شود.

وقتی سیستمی با داده نمونه‌برداری شده یا سیگنال دیجیتال $$ r ^ {*} (t)$$ داشته باشیم، نمودار بلوکی متناظر با آن به صورت شکل ۱ خواهد بود.

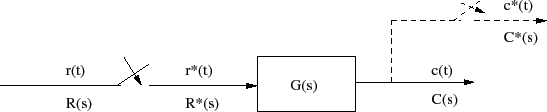
خروجی سیستم $$ C ( s) = G ( s ) R ^ {*} ( s) $$ است. به سختی می‌توان با تابع تبدیل سیستم بالا کار کرد، زیرا شامل ترکیبی از مؤلفه‌های آنالوگ و دیجیتال است. بنابراین، برای سادگی کار کردن با آن، می‌توان مشخصه‌های سیستم را با یک تابع تبدیل توصیف کرد که $$ r ^ { *} ( t) $$ را به $$ c ^ { *} ( t) $$ مربوط می‌کند.

می‌توان نوشت:

$$ \large
C ^ { * } ( s ) = \sum _ { k = 0 } ^ { \infty } c ( k T ) e ^ { - k T _ { s } }
$$

از آنجایی که $$ c (k T ) $$ متناوب است، داریم:

$$ \large
C ^ { * } ( s ) = \frac { 1 } { T } \sum _ { n = - \infty } ^ { \infty } C \left ( s + j n w _ { s } \right ) \text {, } \quad c ( 0 ) = 0
$$

به طریق مشابه، داریم:

$$ \large
\begin {aligned} R^ { * } ( s ) & = \frac { 1 } { T } \sum _ { n = - \infty } ^ { \infty} R \left ( s + j n w _ { s } \right ) \\ { C ^ { * } ( s ) } & = \frac { 1 } { T } \sum _ { n = -\infty } ^ { \infty } C \left ( s + j n w _ { s } \right ) \\ & { = \frac { 1 } { T } \sum _ { n = - \infty } ^ { \infty } R ^ { * } \left ( s + j n w _ { s } \right ) G \left ( s + j n w _ { s } \right ) } \end {aligned}
$$

از آنجایی که $$ R ^ {*} ( s ) $$ متناوب است، داریم: $$ R ^ * ( s + j n \omega _s ) = R ^ * (s) $$. در نتیجه:

$$ \large
\begin {aligned} C ^ { * } ( s ) & = \frac { 1 } { T } \sum _ { n = - \infty } ^ { \infty } R ^ { * } ( s ) G \left ( s + j n w _ { s } \right ) \\ & = R ^ { * } ( s ) \frac { 1 } { T } \sum _ { n = -\infty } ^ { \infty } G \left ( s + j n w _ { s } \right ) \end {aligned}
$$

اگر تعریف کنیم:

$$ \large
G ^ { * } ( s ) = \frac { 1 } { T } \sum _ { n = - \infty } ^ { \infty } G \left ( s + j n w_{s}\right) $$

آنگاه:

$$ \large \begin{align*} C ^ { * } ( s ) & = R ^ { * } (s ) G ^ { * } ( s ) \\ G ^ { * } ( s ) & = \frac { C ^ { * } ( s ) } { R ^ { * } ( s ) } \end {align*}
$$

که به عنوان تابع تبدیل پالسی شناخته می‌شود.

اکنون، اگر $$ z = e ^ {Ts} $$ را در عبارت قبلی جایگذاری کنیم، مستقیماً به تابع تبدیل $$ G (z) $$ خواهیم رسید:‌

$$ \large
G ( z ) = \frac { C ( z ) } { R ( z ) }
$$

همچنین، $$ G (z) $$ را می‌توان به صورت زیر نیز تعریف کرد:

$$ \large
G ( z ) = \sum _ { k =0 } ^ { \infty } g ( k T ) z ^ { - k }
$$

که در آن، $$ g ( k T ) $$ دنباله پاسخ ضربه $$ g ( t) $$ تابع تبدیل $$ G (s) $$‌ سیستم را نشان می‌دهد. دنباله $$ g (k T) $$ با $$ k = 0, 1 , ... $$ به عنوان یک دنباله ضربه شناخته می‌شود.

در نتیجه می‌توان گفت:

1. تابع تبدیل پالسی پالسی یا تابع تبدیل Z، سیستم گسسته را تنها در لحظات نمونه‌برداری نشان می‌دهد. به عبارت دیگر، اطلاعات خروجی بین لحظات نمونه‌برداری از دست می‌رود.
2. از آنجایی که ورودی سیستم گسسته با خروجی یک نمونه‌بردار توصیف می‌شود، برای همه موارد عملی، می‌توان به سادگی نمونه‌بردار را $$ r ^ * (t) $$ در نظر گرفت.

یک راه دیگر برای رسیدن به $$ G ( z ) = \frac { C ( z) } { R ( z ) } $$ به صورت زیر است (وقتی $$ r ^ * (t)$$ یک تابع ضربه باشد):

$$ \large
\begin {aligned} c ^ { * } ( t ) & = \left . g ^ {*} ( t ) \right |_ {\text { when } r ^ { * } ( t ) \text { is an impulse function }} \\ & = \sum _ { k = 0 } ^ { \infty } g ( k T ) \delta ( t - k T ) \end {aligned}
$$

وقتی ورودی $$ r ^ * ( t) $$ است، داریم:

$$ \large
\begin {aligned} c ( t ) & = r ( 0 ) g ( t ) + r ( T ) g ( t - T ) + \ldots \\ \Rightarrow c ( k T ) & = r ( 0 ) g ( k T ) + r ( T ) g ( ( k - 1 ) T ) + \ldots \\ \Rightarrow c ( k T) & = \sum _ { n = 0 } ^ { k } r ( n T ) g ( k T - n T ) \\ \Rightarrow C ( z ) & = \sum _ { k = - \infty } ^ { \infty } \sum _ { n = 0 } ^ { k } r ( n T ) g ( k T - n T ) z ^ { - k } \end {aligned}
$$

با استفاده از قضیه کانوولوشن حقیقی، داریم:

$$ \large C ( z ) = R ( z ) G ( z ) $$

در نتیجه:

$$ \large G ( z ) = \frac{C(z)}{ R (z)}$$

تابع تبدیل پالسی با اجزای متوالی

سیستمی را در نظر بگیرید که دارای اجزای متوالی است. دو حالت زیر را در نظر می‌گیریم:

1. اجزای متوالی با یک نمونه‌بردار جدا شده‌اند.
2. اجزای متوالی با نمونه‌بردار جدا نشده‌اند.

نمودار بلوکی حالت اول مطابق شکل ۲ است.

روابط ورودی-خروجی دو سیستم $$ G _ 1 $$ و $$ G _ 2 $$ به صورت زیر بیان می‌شود:

$$ \large D ( z ) = G _ 1 ( z ) R ( z ) $$

و

$$ \large C ( z ) = G _ 2 ( z ) D ( z ) $$

در نتیجه، رابطه ورودی-خروجی کل سیستم برابر است با:

$$ \large C ( z ) = G _ 1 ( z ) G _ 2 ( z ) R ( z ) $$

بنابراین، می‌توان نتیجه گرفت که تابع تبدیل z دو سیستم خطی که با یک نمونه‌بردار جدا شده‌اند، برابر با ضرب دو تابع تبدیل z آن‌ها است.

نمودار بلوکی حالت دوم در شکل ۳ نشان داده شده است.

خروجی پیوسته $$ C ( s) $$ را می‌توان به صورت زیر نوشت:

$$ \large C ( s ) = G _ 1 ( s) G _ 2 ( s) R ^ * (s) $$

خروجی نمونه‌بردار فرضی برابر است با:

$$ \large C ( z ) = Z [G _ 1 (s) G _ 2 ( s) ] R ( z ) $$

تبدیل z ضرب $$ G _ 1 (z) G _ 2 (z)$$ به صورت زیر است:

$$ \large Z [G_1(s) G _ 2 (s) ] = G _ 1 G _ 2 (z) = G _ 2 G _ 1 ( z ) $$

توجه کنید که جز برای چند حالت خاص، در حالت کلی $$ G_1 G _ 2 (z) \neq G _ 1 (z) G _ 2 (z) $$. بنابراین، خروجی کلی برابر است با:

$$ \large C ( z ) = G _ 1 G _ 2 ( z ) R ( z ) $$

تابع تبدیل پالسی نگهدار مرتبه صفر (ZOH)

تابع تبدیل نگهدار مرتبه صفر (Zero-order Hold) به صورت زیر است:

$$ \large G _ {ho} (s) = \frac { 1 - e ^ { - T s } } {s } $$

بنابراین، تابع تبدیل پالسی آن به صورت زیر خواهد بود:

$$ \large \begin {aligned} G _ { h o } ( z ) & = Z \left [ \frac { 1 - e ^ { - T s } } { s } \right ] \\ & = \left ( 1 - z ^ { - 1 } \right ) Z \left [ \frac { 1 } { s } \right ] \\ & = \left ( 1 -z ^ { - 1 } \right ) \frac { z } { z - 1 } \\ & = 1 \end {aligned}
$$

این نتیجه مورد انتظار بود، زیرا نگهدار مرتبه صفر، سیگنال گسسته را برای یک دوره نمونه‌برداری نگه می‌دارد، بنابراین، تبدیل z نگهدار مرتبه صفر سیگنال نمونه‌برداری شده اصلی‌اش را نتیجه می‌دهد.

یک پیکربندی رایج در سیستم گسسته این است که مطابق شکل ۴، یک دستگاه نمونه‌بردار و نگهدار (S/H) قبل از سیستم خطی با تابع تبدیل $$ G (s) $$ قرار دهیم. اکنون می‌خواهیم رابطه بین $$ r^*(t)$$ و $$ c ^ * (t) $$ را پیدا کنیم.

تبدیل z خروجی $$ c (t) $$ برابر است با:

$$ \large \begin {aligned} C ( z ) & = Z \left [ G _ { h o } ( s ) G ( s ) \right ] R ( z ) \\ & = Z \left [ \frac { 1 - e ^ { - T s } } { s } G ( s ) \right ] R ( z ) \\ & = \left ( 1 - z ^ { - 1 } \right ) Z \left [ \frac { G ( s ) } { s } \right ] R ( z ) \end {aligned} $$

که در آن، $$ (1- z ^ { - 1} ) Z \left[ \frac { G (s)} { s } \right] $$ تابع تبدیل z دستگاه نمونه‌بردار/نگهدار و سیستم خطی است.

قبلاً گفتیم که وقتی فرکانس نمونه‌برداری به بی‌نهایت میل کند، یک سیستم گسسته را می‌توان به عنوان سیستمی پیوسته در نظر گرفت. البته، این بدان معنی نیست که اگر سیگنال $$r(t)$$ با یک نمونه‌بردار ایده‌آل نمونه‌برداری شود، آنگاه $$ r ^*(t)$$ را با قرار دادن زمان نمونه‌برداری $$T$$ برابر با صفر به $$r(t)$$ رساند. اگر خروجی سیگنال نمونه‌برداری شده از یک دستگاه نمونه‌بردار عبور کند، می‌توان با صفر قرار دادن زمان نمونه‌برداری $$T$$، سیگنال اصلی $$r(t)$$ را بازیابی کرد. با توجه به شکل ۴، داریم:

$$ \large \lim _ {T \to 0 } H ( s) = R (s ) $$

مثال

ورودی $$ r ( t) = e ^ { - a t } u _ s ( t ) $$ را در نظر بگیرید که در آن، $$ u _ s ( t) $$ تابع پله واحد است.

تبدیل لاپلاس این ورودی به صورت زیر است:

$$ \large R (s) = \frac { 1 } { s + a } $$

تبدیل لاپلاس سیگنال نمونه‌برداری شده $$ r ^ * ( t) $$ نیز برابر است با:‌

$$ \large R ^ * ( s) = \frac { e ^ { T s } } { e ^ { T s } - e ^ { - a T } } $$

تبدیل لاپلاس خروجی بعد از ZOH به صورت زیر است:

$$ \large \begin {aligned} H ( s ) & = G _{ h o } ( s ) R ^ { * } ( s ) \\ & = \frac { 1 - e ^ { - T s } } { s } \cdot \frac { e ^ { T s } } { e ^ { T s } - e ^ { - a T } } \end {aligned} $$

وقتی $$ T $$ به صفر میل کند، داریم:

$$ \large \lim _ {T \to 0 } H ( s ) = \lim _ { T \ to 0 } = \frac { 1 - e ^ { - T s } } { s } \frac { e ^ { T s }} { e ^ { T s } - e ^ { - a T } } $$

حد بالا را می‌توان با استفاده از قاعده هوپیتال محاسبه کرد. طبق این قاعده، اگر $$ \lim _ { x \to a } f ( x ) = 0 / \infty $$ و $$ \lim _ { x \to a } g ( x ) = 0 / \infty $$، آنگاه $$ \lim _ { x \to a } \frac { f (x)} {g(x)} = \lim _ { x \to a } \frac { f'(x)}{g'(x)} $$.

در این مثال، $$ x = T $$، $$ f ( T ) = \frac { 1 - e ^ { - T s } } { s } $$ و $$ g ( T ) = \frac {e ^ {Ts} - e ^ { - a T } } { e ^ { T s } } $$. وقتی $$ T $$ به صفر میل می‌کند، این عبارت‌ها نیز به صفر میل می‌کنند. بنابراین:‌

$$ \large \begin {aligned} H ( s ) & = \lim _ { T \rightarrow 0 } \frac { f ( T ) } { g ( T ) } \\ & = \lim _ { T \rightarrow 0 } \frac { f ^ { \prime } ( T) } { g ^ { \prime } ( T ) } \\ & = \lim _ { T \rightarrow 0 } \frac { e ^ { T s } } { ( s + a ) e ^ { -T ( s + a ) } } \\ & = \frac { 1 } { s + a } \\ & = R ( s ) \end {aligned} $$

این بدان معنی است که در صورت میل کردن دوره نمونه‌برداری به صفر، می‌توان سیگنال اصلی را از خروجی دستگاه نمونه‌بردار و نگهدار  بازیابی کرد.

تابع تبدیل پالسی سیستم حلقه‌بسته

همان‌طور که می‌دانیم، فیدبک در سیستم‌های کنترل حلقه‌بسته مزایای زیادی دارد.

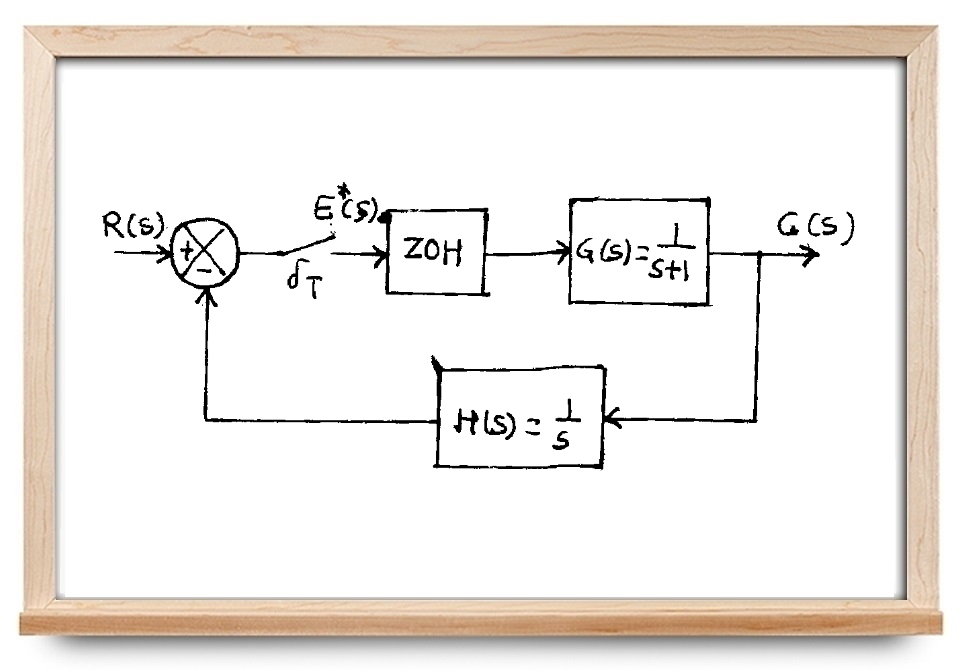
شکل ۵ یک سیستم حلقه‌بسته را با یک نمونه‌بردار در مسیر پیش‌رو نشان می‌دهد.

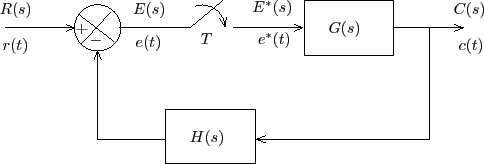
می‌خواهیم رابطه بین ورودی و خروجی این سیستم را بنویسیم. در سیستم بالا، خروجی نمونه‌بردار به عنوان ورودی سیستم عمل می‌کند. ورودی نمونه‌بردار نیز به عنوان یک خروجی دیگر در نظر گرفته می‌شود. بنابراین، روابط ورودی-خروجی را می‌توان به صورت زیر نوشت:‌

$$ \large \begin {align*}
E ( s ) & = R ( s ) - G ( s) H ( s) E ^ * (s) \\
C ( s) & = G ( s) E ^ * ( s )
\end {align*} $$

با تبدیل پالس گرفتن از دو سمت رابطه بالا داریم:

$$ \large \begin {align*}
E ^ * ( s ) & = R ^ * ( s ) - G H ^ * ( s) E ^ * (s)
\end {align*} $$

که در آن:

$$ \large \begin {align*}
G H ^ * ( s ) & = [ G ( s ) H ( s ) ] ^ * \\
& = \frac { 1 } { T } \sum _{n = - \infty } ^ { \infty } G ( s + j n \omega _ s ) H ( s + j n \omega _ s )
\end {align*} $$

معادله حاصل از تبدیل پالس را می‌توانیم به صورت زیر بنویسیم:

$$ \large \begin {align*}
E ^ * ( s) & = \frac { R ^ * (s) } { 1 + GH ^ * ( s ) } \\
\Rightarrow C ( s ) & = G ( s) E ^ * (s) \\
& = \frac { G (s) R ^ * ( s ) } { 1 + G H ^ * (s) }
\end {align*} $$

با تبدیل پالس گرفتن از رابطه بالا، داریم:

$$ \large \begin {align*}
C ^ * ( s ) & = [ G ( s) E ^ * (s) ] ^ * \\
& = G ^ * ( s) E ^ * (s) \\
& = \frac { G ^ * (s) R ^ * ( s ) } { 1 + G H ^ * (s) }
\end {align*} $$

و در نتیجه:

$$ \large \begin {align*}
& \frac { C ^ * ( s ) } {R ^ * (s) }
= \frac { G ^ * (s) } { 1 + G H ^ * (s) } \\
& \Rightarrow \frac { C ( z ) } {R ( z ) }
= \frac { G (z) } { 1 + G H ( z ) }
\end {align*} $$

که در آن، $$ G H ( z ) = Z [G ( s) H ( s ) ] $$.

اکنون اگر نمونه‌بردار را در مسیر فیدبک قرار دهیم، نمودار بلوکی به صورت شکل ۶ خواهد بود.

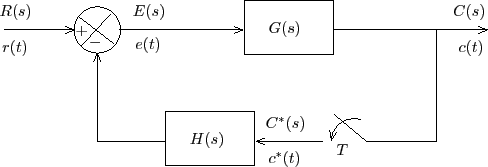
روابط ورودی-خروجی این سیستم را می‌توان به صورت زیر نوشت:‌

$$ \large \begin {align*}
E ( s) & = R ( s) - H ( s ) C ^ * ( s) \\
C ( s) & = G ( s) E ( s) = G ( s ) R ( s ) - G (s ) H ( s) C ^ * ( s)
\end {align*} $$

با اعمال تبدیل پالسی بر این روابط، داریم:‌

$$ \large \begin {align*}
E ^ * ( s) & = R ^ * ( s) - H ^ * ( s ) C ^ * ( s) \\
C ^ * ( s) & = G R ^ * ( s ) - G H ^ * ( s) C ^ * ( s)
\end {align*} $$

که در آن:

$$ \large \begin {align*}
G R ^ * (s ) & = [G ( s) R ( s ) ] ^ * \\
G H ^ * ( s) & = [G ( s) H ( s) ] ^ *
\end {align*} $$

در نتیجه، می‌توان نوشت:

$$ \large \begin {align*}
C ^ * & = \frac { G R ^ * (s ) } {1 + G H ^ * (s) } \\
\Rightarrow C ( z ) & = \frac { G R ( z ) } {1 + G H ( z ) }
\end {align*} $$

توجه کنید که نمی‌توان تابع تبدیل ورودی-خروجی این سیستم را با $$ \frac { C ^ * (s)} { R ^ * (s)}$$ یا $$ \frac { C ( z)} { R (z)}$$ تعریف کرد. از آنجایی که ورودی $$ r ( t) $$ نمونه‌برداری نشده است، سیگنال نمونه‌برداری شده $$ r ^ * ( t) $$  وجود ندارد. خروجی پیوسته $$ C ( s) $$ را می‌توان بر اساس ورودی توصیف کرد:

$$ \large C ( s) = G ( s ) R ( s) - \frac { G ( s) H ( s) } { 1 + G H ^ * ( s) } G R ^ * (s) $$

معادله مشخصه

معادله مشخصه نقش مهمی در مطالعه سیستم‌های خطی ایفا می‌کند. همان‌طور که می‌دانیم، یک سیستم گسسته LTI مرتبه $$n$$ را می‌توان با یک معادله تفاضلی مرتبه $$n$$ نمایش داد:

$$ \large c ( k + n ) + a _ { n - 1 } c ( k + n - 1) + a _ { n -2 } c ( k + n - 2 ) + \cdots + a _ 1 c ( k + 1 ) + a _ 0 c ( k ) \\ \large
= b _ m r ( k + m ) + b _ {m-1} r ( k + m - 1) + \cdots + b _ 0 r ( k ) $$

که در آن، $$ r ( k ) $$ و $$ c ( k ) $$ به ترتیب، دنباله‌های ورودی و خروجی را نشان می‌دهند.

رابطه ورودی-خروجی را می‌توان با گرفتن تبدیل z از هر دو طرف معادله بالا با شرایط اولیه صفر به صورت زیر نوشت:

$$ \large \begin {align*}
G ( z ) & = \frac { C ( z )} { R (z ) } \\
& = \frac { b _ m z ^ m + b _ { m -1 } z ^ { m - 1 } + \cdots + b _ 0 } { z ^ n + a _ { n -1 } z ^ { n -1 } + \cdots + a _ 1 z + a _ 0 }
\end {align*} $$

معادله مشخصه با صفر قرار دادن مخرج $$ G ( z ) $$ به دست می‌آید:

$$ \large \begin {align*}
{ z ^ n + a _ { n -1 } z ^ { n -1 } + \cdots + a _ 1 z + a _ 0 } = 0
\end {align*} $$

مثال

تابع تبدیل مسیر پیش‌رو $$ G ( s) = \frac { 2 } { s ( s + 2 ) }$$ و تابع تبدیل فیدبک $$1 $$ را در نظر بگیرید. اگر نمونه‌بردار در مسیر پیش‌رو قرار داشته باشد، معادله مشخصه سیستم را برای زمان نمونه‌برداری $$ T = 0.1$$ ثانیه به دست آورید.

حل:

$$ \large \frac { C ( z ) } { R ( z ) } = \frac { G ( z ) } { 1 + G H ( z ) } $$

از آنجایی که تابع تبدیل فیدبک برابر با $$ 1$$ است، داریم:

$$ \large \begin {aligned} G ( z ) = G H ( z ) & = z \left [ \frac { 2 } { s ( s + 2 ) } \right ] \\ & = \frac { 2 } { 2 } \frac { \left ( 1 - e ^ { - 2 T } \right ) z } { ( z - 1 ) \left ( z - e ^ { - 2 T } \right ) } \\ & = \frac { 0 . 1 8 z } { z ^ { 2 } - 1 . 8 2 z + 0 . 8 2 } \\ \Rightarrow & \frac { C ( z ) } { R ( z ) } = \frac { 0 . 1 8 z } { z ^ { 2 } - 1 . 6 4 z + 0 . 8 2 } \end {aligned} $$

بنابراین، معادله مشخصه سیستم $$ z ^ 2 - 1.64 z + 0.82 = 0 $$ است.

اگر مطلب بالا برای شما مفید بوده و علاقه‌مند به موضوعات مرتبط با آن‌ هستید، پیشنهاد می‌کنیم آموزش‌های زیر را نیز ببینید:

• آموزش نمونه برداری و بازسازی اطلاعات در سیستم های کنترل دیجیتال
• سیستم غیر خطی — راهنمای جامع
• کنترل پیش بین مدل (MPC) — راهنمای جامع
• کنترل بهینه در متلب — از صفر تا صد

^^