اصل لانه کبوتر – به زبان ساده
در این آموزش از مجله فرادرس، اصل لانه کبوتر را معرفی میکنیم. «قضیه لانه کبوتر» که بهدلیل بدیهی بودن، بهنام اصل لانه کبوتر شناخته میشود (اصل، بدونِ اثبات و بهصورت پیشفرض پذیرفته میشود و قضیه، گزارهای است که براساس گزارهها و اصول پذیرفتهشده پیشین اثبات شده است)، یکی از قضایای ساده و البته پرکاربرد در ریاضیات است.

اصل لانه کبوتر، بار اول توسط یوهان «پیتر گوستاو لوژِن دیریکله» معرفی شد و «فرانک رمزی» آن را توسعه داد. این اصل را اصل کِشوی دیریکله یا اصل حجرهها نیز مینامند.
قبل از تعریف رسمی اصل لانه کبوتر، مثالی را بیان میکنیم که به درک آن کمک زیادی میکند. فرض کنید در یک کلاس درس، ۱۳ دانشآموز حضور دارند. درباره این کلاس میتوان گفت که حداقل دو نفر وجود دارد که ماه تولد آنها یکسان باشد (احتمالاً با خود فکر میکنید که این، بدیهی است). به عبارت دیگر، دو عضو از مجموعه دانشآموزان حاضر در کلاس، وضعیت یکسانی دارند. دقت کنید که ما فقط گفتیم حداقل دو نفر وجود دارند که در یک ماه متولد شدهاند. اما درباره نحوه توزیع ماهها نمیتوانیم چیزی بگوییم. ممکن است هر 13 نفر در یک ماه متولد شده باشند. این مثال، دقیقاً همان اصل لانه کبوتری است؛ فقط کافی است دانشآموزان را کبوتر و ماهها را لانه فرض کنید.

قضیه لانه کبوتر
اگر کبوتر، لانه را اشغال کنند و تعداد کبوترها بیشتر از تعداد لانهها باشد ()، آنگاه طبق اصل لانه کبوتری، حداقل یک لانه وجود خواهد داشت که حداقل دو کبوتر در آن است.
اثبات: این قضیه را با استفاده از برهان خلف اثبات میکنیم که در آموزشهای قبلی مجله فرادرس بیان شد. بنابراین، طبق برهان خلف فرض کنید قضیه صحیح نیست و در هیچیک از لانهها، بیش از یک کبوتر وجود ندارد. بنابراین، حداکثر کبوتر داریم. این تعداد کبوتر، با فرض که ابتدا بیان کردیم، در تناقض است. در نتیجه، فرض خلف اشتباه و قضیه صحیح بوده و اثبات آن کامل میشود.
همانگونه که میبینیم، اصل لانه کبوتری ظاهر سادهای دارد، اما باید توجه داشت که مهمترین نکته در حل مسائل با استفاده از آن، تعریف مناسب لانهها و کبوترها است.
در ادامه، چند مثال را بررسی میکنیم.
مثال ۱
۱۱ عدد طبیعی داریم که مقدار آنها را نمیدانیم. ثابت کنید رقم یکان دو عدد از این اعداد، یکسان است.
حل: میدانیم که یکان هر عدد طبیعی، یکی از ارقام 0 تا ۹ است (تعداد 10 رقم). در این مثال، 11 عدد را به عنوان ۱۱ کبوتر و ارقام 0 تا 9 را بهعنوان لانهها در نظر میگیریم. از آنجایی که تعداد کبوترها، بیشتر از تعداد لانهها است ()، حداقل یک لانه داریم که در آن، حداقل دو کبوتر قرار دارد. به عبارت دیگر، حداقل دو عدد داریم که رقم یکان آنها یکسان است. بنابراین، اثبات کامل میشود.
مثال 2
پنج نقطه درون یک مربع به ضلع ۱ وجود دارد. ثابت کنید حداقل فاصله دو نقطه از این پنج نقطه، کمتر از است.
حل: ابتدا مربع را به چهار قسمت مساوی تقسیم میکنیم. در ادامه، ۴ مربع کوچک را بهعنوان لانه و ۵ نقطه را بهعنوان کبوترها در نظر میگیریم. خطوط مرزی مربعها را نیز مشترک فرض میکنیم. طبق اصل لانه کبوتر، حداقل ۲ نقطه از نقطهها به یکی از مربعهای کوچک تعلق دارند.
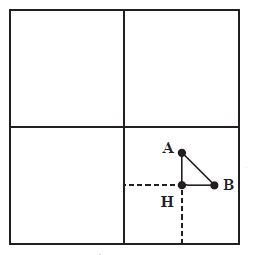
حال که میدانیم حداقل دو نقطه در یکی از مربعها وجود دارد، باید اثبات کنیم فاصله آن دو کمتر از است.
طول هریک از مربعهای کوچک، است. با توجه به شکل بالا و با کمک قضیه فیثاغورس، داریم:
از آنجایی که طولهای AH و BH کوچکتر از است، میتوانیم نامعادله زیر را بنویسیم:
در نتیجه، داریم:
مثال ۳
در یک مهمانی، باید حداقل چند نفر حضور داشته باشند بهگونهای که حرف اول نام، ماه تولد و جنسیت دو نفر از آنها یکسان باشد؟
حل: برای حرف اول نام 32 حالت، ماه تولد 12 حالت و جنسیت ۲ حالت وجود دارد. یعنی تعداد کل حالات برابر با است. افراد را کبوتر و حالات ممکن را لانه در نظر میگیریم. پس طبق اصل لانه کبوتری، باید باشد. یعنی حداقل نفر باید در مهمانی حضور داشته باشند.
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^













خدا خیرتون بده ♥️
با سلام ،اگر چهار نقطه رو در سمت بالا راست یک مربع به ضلع 1 با ا فاصله ناچیز از یکدیگر در نظر بگیریم ،آنگاه نقطه ی دیگر را در سمت چپ پایین در نظر بگیریم ،آنگاه حدائقل دو نقطه نخواهیم داشت که فاصله ی آنها از یکدیگر کمتر از رایکال دو دوم شود.
این طور نیست؟
نه در صورت سوال گفته در این حالت “حداقل” دو نقطه خواهیم داشت که فاصله شون کم تر از رادیکال دو دوم بشه در این حالتی که شما مطرح کردید سه نقطه رو در یک گوشه نزدیک به هم قرار دادید در این حالت در واقع سه نقطه داریم که دو به دو فاصله شون کم تر از رادیکال دو دوم میشه
ممنون از توضیح خوبتون واقعا عالی بود مرسی?
سلام خسته نباشید
من جایی خوندم که بازی slither link را میتوان به کمک این اصل حل کرد ولی ربط این اصل را با این بازی متوجه نشدم .
میشه لطفاً راهنمایی کنید
ممنون از مطالبتون
سلام-فرض کنیم که درکیسه ای 7 توپ سفید و8 توپ سیاه و2 توپ سبز وجود دارد.شخصی بدون نگاه کردن به این توپها ، آنها را بیرون می اندازد.حداقل چند توپ را باید از کیسه بیرون بکشد،تا مطمئن شود، 3 توپ از یک رنگ بیرون آورده است؟
طبق این اصل لانه کبوتری چگونه باید حل کنیم.لطفا” نکات را مو به مو با جزئیات بگویید تا آموزشی در این زمینه باشد.باتشکر
7 ta
bebin bayad badtarin halat ro darnazar begirim yani begim az top sabz 2 tasho begirim 2 ta ham meshki va 2 ta ham sefid khob ta alan ma 6 ta top entekhab kardim age 1 top gige biron biarim ghtaan 3 ta top hamrang darim
بسیار عالی هستن من هم اصل لانه کبوتری و هم جایگشت و ترکیب را بسیار خوب فهمیدم خسته نباشید
سلام
در مثال دومی که زدید،اولا ما مقدار AH و BH رو دقیقا نمیدونیم فقط میدونیم کوچکتر از یک دوم هست.پس نباید به جای اونها یک دوم قرار بدید.بعدش مگه ما مقدار AB رو میدونیم که نوشتید کوچکتر از AH و BH هست؟!
بر فرض درستی تا اینجای کار قضیه فیثاغورس نتیجه میده AB برابر است با رادیکال یک دوم.رادیکال یک دوم چه عددی در میاد؟رادیکال دو دوم چه عددی در میاد؟چطور برابر با رادیکال دو دوم است؟
سلام.
همانطور که خودتان نیز اشاره کردهاید، مقادیر AH و BH کوچکتر از 21 هستند و به همین دلیل، در رابطهٔ فیثاغورس بهجای مساوی از علامت کوچکتر استفاده کردهایم. به این ترتیب و با کمک رابطه فیثاغورس، به این نتیجه رسیدهایم که AB باید از مقدار 22 کوچکتر باشد. برای پاسخ پرسش دومتان، نامساوی (AB)2<21 را در نظر بگیرید. اگر از دو طرف این نامساوی رادیکال بگیریم، خواهیم داشت: (AB)2<21. بنابراین: (AB)<21. حال با توجه به 21=21=2×21×2=22، به رابطه نهایی AB<22 میرسیم.