آونگ ساده در فیزیک — مفاهیم پایه

آونگ ساده سیستمی است که معمولا به منظور توصیف و تعریف حرکت هارمونیک از آن استفاده می‌شود. حرکت هارمونیک نیز به حرکتی اطلاق می‌شود که با الگوی خاصی و به طور مداوم با زمان تکرار می‌شود. در این مطلب قصد داریم تا نحوه بدست آوردن دوره تناوب آونگ را توضیح داده و مفاهیم مرتبط با آن را تعریف کنیم. البته پیشنهاد می‌شود به منظور درک بهتر، مطالب ارتعاشات و موج‌های سینوسی را مطالعه فرمایید.

آونگ ساده چیست؟

یک آونگ ساده از یک کره کوچک به همراه یک سیم تشکیل شده است. توجه داشته باشید که سیم بسیار نازک و به صورتی فرض شده که کش نیاید. البته ممکن است یک توزیع پیوسته جرم نیز نوسان کند که آن را نهایتا به صورت یک جرم و سیم مدل‌سازی می‌کنند. در شکل زیر زیر نحوه مکانیزم کارکرد آونگ در ساعت دیواری نشان داده شده است.

فیلم آموزش فیزیک – پایه دوازدهم در فرادرس

کلیک کنید

به منظور بررسی سیستم، آونگی را در زاویه θ در نظر بگیرید که نیرو‌های کششِ T و نیروی گرانش به آن وارد می‌شود. در شکل زیر شماتیکی از یک آونگ ساده به همراه نیرو‌های وارد شده به آن نشان داده شده است.

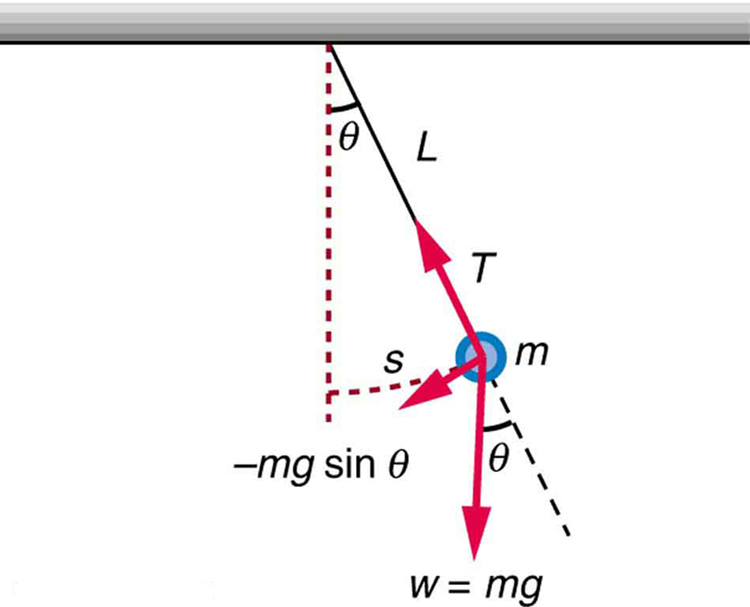
جابجایی از حالت تعادل یا همان طول قوس، با s نشان داده می‌شود. با توجه به مفاهیم مثلثات نیرویی که منجر به نوسان جرم می‌شود برابر با $$-\text {mg} \phantom { \rule {0.25em} {0ex}}\text {sin} \theta$$ است. این نیرو همواره در تلاش است تا جرم را به حالت تعادلش نزدیک کند.

معمولا از آونگ ساده یا پاندول در ساعت‌های دیواری، اسباب‌ بازی و حتی در ماهواره‌ها استفاده می‌شود. معادلات یک آونگ ساده را می‌توان با فرض نوسان با زاویه‌ اندک به راحتی برآورد کرد. اما در حالتی که زاویه نوسان زیاد باشد، معادلات غیر خطی شده و حل کردن آن‌ها آسان نخواهد بود.

حال فرض کنید زاویه نوسان جرم آویزان بسیار اندک است. در این صورت می‌توان از تقریب زیر استفاده کرد.

$$\Large F = - m g \sin \theta \xrightarrow {sin \theta \approx \theta} F = - m g \theta$$
رابطه ۱

از طرفی جابجایی s متناسب با θ است. زمانی که θ بر حسب رادیان بیان شود، طول s را می‌توان به صورت زیر محاسبه کرد.

$$\Large s = \mathrm{L\theta }$$

بنابراین زاویه جابجایی برابر است با:

$$\Large \theta = \frac{ s } { L }$$

با قرار دادن زاویه بدست آمده در رابطه ۱، نیروی F به صورت زیر بدست خواهد آمد.

$$\Large F \approx - \frac {\text{mg}} { L } s$$

رابطه بدست آمده ما را به یاد قانون هوک می‌اندازد. این قانون، رابطه بین افزایش طول فنر و سختی آن را به صورت زیر بیان می‌کند.

$$\Large F = - \text {kx}$$

بنابراین نوسان یک آونگ ساده همچون نوسان جرم و فنری با سختی $$\large k = \frac { m g } { L }$$ بوده که جابجایی لحظه‌ای آن نیز برابر با $$\large x = s$$ است. البته این فرضیات تا زاویه کم‌تر از ۱۵ درجه درست هستند.

برای یک آونگ ساده کمیتی تحت عنوان دوره تناوب (T) معادل با زمان یک نوسان کامل تعریف می‌شود. زمان یک نوسان کامل برای آونگی به طول L که در شتاب گرانشی g قرار گرفته، برابر است با:

$$\Large T = 2 \pi \sqrt {\frac { m } { k } } = 2 \pi \sqrt{\frac {m}{\text{mg}/L}}$$

نهایتا با ساده کردن رابطه فوق، دوره تناوب یک آونگ ساده به صورت زیر بدست می‌آید.

$$\Large T=2\pi \sqrt{\frac{L}{g}}$$
رابطه ۲

نکته جالب در مورد رابطه فوق این است که دوره تناوب یک آونگ تنها به طول آن و شتاب گرانشیش وابسته است. در حقیقت دو آونگ ساده با طول‌های یکسان و جرم‌های متفاوت، دوره تناوب‌های یکسانی دارند.

به دست آوردن اختلاف ارتفاع در آونگ

برای به دست آوردن ارتفاع آونگ پس از اینکه از نقطه تعادل خود به اندازه زاویه $$\theta$$ جابه‌جا می‌شود کافی است از روابط حاکم بر تجزیه بردارها استفاده کنیم. بدین ترتیب اگر ارتفاع آونگ را در نقطه تعادل یا زمانی که $$\theta=0$$ است برابر با L در نظر بگیریم، بعد از انحراف آونگ به اندازه $$\theta$$ طول آونگ برابر با $$L\cos\theta$$ است. حال برای به دست آوردن اختلاف ارتفاع در آونگ کافی است مانند زیر عمل کنید و داریم:

فیلم آموزش فیزیک پایه 1 – جامع و کاربردی در فرادرس

کلیک کنید

$$\large\begin{cases}h_{0}=L \\ h_{1}=L\cos\theta\end{cases}$$
$$\large\Delta h=h_{0}-h_{1}=L(1-\cos\theta)$$

مثال

فرض کنید آونگی به طول 75 سانتی متر در یک سیاره مجهول قرار داده شده است. با فرض این‌که زمان یک نوسان کامل برای این آونگ برابر با ۱.۷۳۵۷ ثانیه باشد، سیاره مجهول را بیابید؟

رابطه ۲ را همان‌طور که در زیر بیان شده، بر حسب g بدست می‌آوریم.

$$\Large \begin {align*} T = 2 \pi \sqrt { \frac { L } { g } } & \Rightarrow g = \frac {4 \pi ^ 2 } { T ^ 2 } L \\ & \Rightarrow g={4\pi }^{2} \frac {0\text{.}\text{75000}\phantom{\rule{0.25em}{0ex}}\text{m}}{{\left(1\text{.}\text{7357 s}\right ) } ^ { 2 } } = 9.8 \ m / s ^ 2 \end {align*}$$

شتاب بدست آمده برابر با $$g = 9.8 \ m / s ^ 2$$ است، بنابراین سیاره مجهول همان زمین است! توجه داشته باشید که تعیین شتاب گرانشی با استفاده از این روش در ماهواره‌ها کاربرد دارد. در آینده بیشتر این کاربرد‌ها را توضیح خواهیم داد. در آینده در مورد نوع پیچیده‌تری از آونگ تحت عنوان آونگ مرکب صحبت خواهیم کرد. در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس فیزیک
• مجموعه آموزش‌های فیزیک و ریاضی
• جسم سیاه در فیزیک -- به زبان ساده
• مشتق - به زبان ساده
• آونگ مرکب — از صفر تا صد
• نظریه جنبشی گاز‌ها — از صفر تا صد