گرد کردن اعداد در ریاضیات | به زبان ساده

اعداد، کلید دسترسی به محاسبات هستند. ولی کار با اعداد اعشاری، مشکل‌تر از اعداد صحیح است. به خصوص ذهن ما برای کار روی اعداد اعشاری، آمادگی کافی ندارد و راحت‌تر است که محاسبات را حتی به طور تقریبی، به کمک اعداد صحیح انجام دهیم. به این منظور، قبل از انجام محاسبات، اعداد مورد محاسبه را «گرد» (Round) می‌کنیم تا به سرعت محاسباتمان بیفزاییم. البته واضح است که با این کار دقت محاسبات را کاهش داده‌ایم. در این نوشتار از مجله فرادرس به موضوع گرد کردن اعداد (Rounding) خواهیم پرداخت و شیوه‌های مختلف آن را بازگو خواهیم کرد. به یاد داشته باشید که گرد کردن هر عدد، هزینه‌ای دارد که همان کاهش دقت در انجام محاسبات است.

برای آشنایی بیشتر با اعداد اعشاری و اعداد صحیح بهتر است نوشتارهای اعداد اعشاری — به زبان ساده و اعداد صحیح — به زبان ساده از مجله فرادرس را مطالعه کنید. همچنین خواندن مطالب توابع جز صحیح — به زبان ساده و تقسیم عدد صحیح — به زبان ساده نیز خالی از لطف نیست.

گرد کردن اعداد در ریاضیات

همانطور که بیان کردیم، «گرد کردن» (Rounding) به معنی ساده‌سازی اعداد است تا محاسبات روی آن‌ها با سرعت و سادگی بیشتر همراه شود. البته این ساده‌سازی، به بهای کاهش دقت در انجام محاسبات همراه است. وقتی عددی را گرد می‌کنیم، مقدار حاصل یا نتیجه اصلی، یک عدد صحیح است که بسیار به عدد اولیه نزدیک است و می‌تواند جایگزینی برای انجام محاسبات باشد.

برای مثال عدد ۷۳ را در نظر بگیرید. اگر این عدد را به نزدیک‌ترین مضرب ۱۰ گرد کنیم، مقدار ۷۰ حاصل می‌شود. به این معنی که ۷۰ نزدیک‌ترین عدد به ۷۳ است که البته مضرب ۱۰ نیز هست. واضح است که اختلاف این دو عدد، ۳ واحد است.

نکته: مضرب‌های ده، اعدادی هستند که رقم یکان آن‌ها صفر باشد.

این بار عدد ۷۸ را در نظر بگیرید. نزدیک‌ترین عدد مضرب ۱۰ به این عدد، ۸۰ است. واضح است که ۸۰ مضرب ۱۰ بوده و فاصله یا اختلاف آن از ۷۸ برابر با ۲ واحد است. همانطور که مشاهده کردید، اعداد ۷۳ و ۷۸ به نزدیک‌ترین عدد مضرب ۱۰ گرد شدند. اگر ۷۳ را به ۸۰ گرد می‌کردیم، فاصله یا اختلافی برابر با ۷ واحد داشتیم. از طرفی اگر ۷۸ را به ۷۰، گرد می‌کردیم، حاصل اختلاف این دو عدد، ۸ واحد بود. بنابراین کمترین فاصله بدست نمی‌آمد.

به این موضوع نیز توجه داشته باشید که اگر عدد A را گرد کنیم و حاصل از A بزرگتر باشد، عمل گرد کردن را به نام «تقریب اضافی» می‌شناسند. برعکس اگر عمل گرد کردن A باعث شود که عدد حاصل از گرد کردن از A کوچکتر باشد، عمل گرد کردن، با «تقریب نقصانی» رخ داده است. انتخاب روش تقریب اضافی یا نقصانی براساس هدف از انجام محاسبات بعدی، صورت می‌گیرد. البته این کار با در نظر گرفتن کمترین میزان خطا همراه است.

برای مثال هنگامی که ریسک یک سرمایه‌گذاری را محاسبه می‌کنیم، معمولا بیشترین میزان ضرر را به عنوان حد تحمل انتخاب می‌کنیم. به این ترتیب از تقریب اضافی کمک می‌گیریم. و اعداد را گرد می‌کنیم. برعکس هنگام محاسبه سود، به علت دخالت عوامل غیر قابل کنترل، معمولا از تقریب نقصانی استفاده کرده تا در بدترین حالت، میزان سود را بدست آورده باشیم.

روش‌های مختلفی برای گرد کردن (چه اعداد صحیح و چه اعداد اعشاری) وجود دارد که در ادامه متن به آن‌ها اشاره خواهیم کرد. جدا از اینکه چه روشی را برای گرد کردن به کار می‌برید، مراحل گرد کردن اعداد به صورت زیر است:

• تعیین تعداد ارقام باقی‌مانده از عدد گرد شده (ارقام معنی‌دار- Significant)
• انتخاب قانون برای حذف ارقام (روش گرد کردن)
• حذف ارقام مورد نظر و نمایش عدد گرد شده
• مشخص کردن میزان خطای حاصل از گرد کردن

البته گرد کردن اعداد& ساده به نظر می‌رسد و همین سادگی، آن را روشی موفق برای سرعت بخشیدن به انجام محاسبات پیچیده و تقریبی کرده است.

گرد کردن اعداد به پایین

بهتر است ابتدا «گردن کردن اعداد به پایین» (Rounding Down) را به کمک یک مثال معرفی کنیم.

مثال ۱

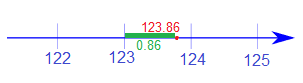
فرض کنید می‌خواهیم عدد ۱۲۳٫۸۶ را به نزدیک‌ترین عدد صحیح و به پایین، گرد کنیم. بنابراین باید ارقام اعشاری حذف شوند. به این ترتیب به سه رقم صحیح احتیاج داریم. از آنجایی که می‌خواهیم عدد ۱۲۳٫۸۶ را به پایین گرد کنیم، بزرگترین عدد صحیح که از 123٫86 کوچکتر یا مساوی است را در نظر می‌گیریم. به این ترتیب حاصل گرد کردن این عدد به نزدیک‌ترین عدد صحیح کوچکتر از آن (گرد کردن به پایین- Round Down)، برابر است با ۱۲۳.

فیلم آموزش محاسبات سریع ریاضی – به زبان ساده + گواهینامه در فرادرس

کلیک کنید

مشخص است که در این حالت، خطای گرد کردن برابر با ۰٫۸۶ است.

$$\large | 123.86 \; - 123 | = 0.86$$

همانطور که در این مثال متوجه شدید، پس از مشخص کردن رقم یا رقم‌های قابل حذف، نحوه گرد کردن عدد به پایین به صورت زیر مشخص می‌شود. علامت این تفاضل (بدون در نظر گرفتن قدر مطلق) نشانه «تقریب اضافی» یا «تقریب نقصانی» است. به این ترتیب اگر حاصل تفاضل عدد نتیجه گرد کردن از عدد اصلی، مثبت باشد، تقریب اضافی و اگر این تفاضل منفی بدست آید، تقریب نقصانی خواهد بود.

قاعده گرد کردن به پایین: گرد کردن یک عدد به پایین، یعنی پیدا کردن بزرگترین عددی که با توجه به تعداد ارقام باقی‌مانده، از عدد مورد نظر کوچکتر یا مساوی باشد.

نکته: اگر با تابع جزء صحیح آشنا باشید، متوجه می‌شوید که گرد کردن اعداد به پایین و نزدیک‌ترین عدد صحیح، دقیقا با «تابع جزء صحیح» (Floor Function) برابر است. به این ترتیب تابع جزء صحیح یک تقریب نقصانی ایجاد می‌کند.

مثال ۲

این بار یک عدد اعشاری را گرد می‌کنیم. فرض کنید همان عدد ۱۲۳٫۸۶ را می‌خواهیم با یک رقم اعشار نمایش دهیم. در نتیجه باید رقم دوم اعشار آن حذف شود. بزرگترین عدد که دارای یک رقم اعشار بوده و از ۱۲۳٫۸۶ نیز کوچکتر است، عدد ۱۲۳٫۸ است. به این ترتیب حاصل گرد کردن ۱۲۳٫۸۶ با یک رقم اعشار بدست آمده و خطای گرد کردن نیز برابر با ۰٫0۶ است.

$$\large | 123.86 \; - 123.8 | = 0.06$$

مثال ۳

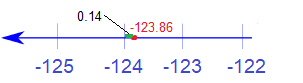
این بار می‌خواهیم با استفاده از قاعده ذکر شده، یک عدد منفی را به پایین گرد کنیم. توجه داشته باشید که روی محور اعداد، هر چه به سمت چپ، حرکت کنیم، عددها کوچکتر خواهند شد. به تصویر ۲ توجه کنید. عدد ۱۲۳٫۸۶- را می‌خواهیم به عدد صحیح، گرد به پایین کنیم. از آنجایی که حاصل باید یک عدد صحیح باشد که از عدد مورد نظر نیز کوچکتر است، به پایین گرد کردن عدد ۱۲۳٫۸۶- حاصلی برابر با ۱۲۴- خواهد داشت. خطای گرد کردن نیز برابر با 0٫۱۴ است.

$$\large | -123.86 \; - (-124) | = 0.14$$

نکته: توجه کنید که میزان خطا همیشه به صورت «قدر مطلق» (Absolute Value) اختلاف مقدار واقعی با مقدار گرد شده حاصل می‌شود.

در ضمن اگر لازم باشد این عدد را با یک رقم اعشار گرد به پایین کنیم، طبق قاعده گرد کردن به پایین حاصل برابر با ۱۲۳٫۹- خواهد بود. بنابراین هر گاه اعداد را روی محور در نظر بگیریم، حاصل گرد کردن به پایین، عددی است که همیشه از عدد اولیه کوچکتر بوده و تقریب نقصانی است. خطای گرد کردن نیز در اینجا برابر با 0٫04 خواهد بود.

گرد کردن اعداد به بالا

«گرد کردن به بالا» (Round Up)، نیز به همان شیوه گرد کردن به پایین اجرا می‌شود ولی با این تفاوت که از میان مقادیر بزرگتر، نزدیکترین مقدار یا کوچکترین آن‌ها با توجه به حذف ارقام مورد نظر، به عنوان مقدار گرده شده، در نظر گرفته می‌شود. باز هم برای روشن شدن موضوع به مثال‌هایی در این زمینه خواهیم پرداخت.

مثال 4

می‌خواهیم عدد ۱۲۳٫86 را به بالا گرد کرده و به صورت یک عدد صحیح نمایش دهیم. واضح است که همه ارقام اعشار آن باید حذف شود.

نزدیک‌ترین اعداد صحیح به ۱۲۳٫۸۶ دو عدد ۱۲۳ و ۱۲۴ هستند ولی چون ۱۲۴ از بین مقادیر بزرگتر از ۱۲۳٫۸۶ از همه کوچکتر است، آن را نتیجه گردن کردن به بالا در نظر می‌گیریم. خطای گرد کردن در اینجا برابر با ۰٫1۴ است. برای مشخص شدن موضوع به تصویر ۱ توجه کنید. البته تصویر ۲ نیز چنین حالتی را برای زمانی که مقادیر منفی باشند، نشان داده است. به این ترتیب قانون برای گرد کردن اعداد به بالا را به صورت زیر در نظر می‌گیریم.

قاعده گرد کردن به بالا: گردن کردن یک عدد به بالا، یعنی پیدا کردن کوچکترین عددی که با توجه به تعداد ارقام باقی‌مانده، از عدد مورد نظر بزرگتر یا مساوی باشد.

مثال ۵

باز هم به سراغ عدد ۱۲۳٫۸۶- می‌رویم و می‌خواهیم آن را به نزدیک‌ترین عدد صحیح و رو به بالا گرد کنیم. مشخص است که طبق تصویر ۲، نتیجه این عمل عدد ۱۲۳- است زیرا کوچکترین عدد صحیح در بین مقادیر بزرگتر از ۱۲۳٫۸۶-، عدد ۱۲۳- خواهد بود. باز هم یادآوری می ‌کنیم که حرکت به سمت راست روی محور، مقادیر بزرگتر را مشخص می‌کند. خطای گرد کردن در این جا برابر با ۰٫۸۶ است.

$$\large | -123.86 \; - (-123) | = 0.86$$

مثال 6

حاصل گرد کردن عدد ۱۲۳٫۸۶- با یک رقم اعشار نیز طبق قاعده گرد کردن به بالا، برابر با ۱۲۳٫8- خواهد بود. واضح است که میزان خطای گرد کردن در این حالت نیز برابر با 0٫06 خواهد بود.

$$\large | -123.86 \; - (-123.8) | = 0.06$$

نکته: همانطور که مشاهده می‌کنید، خطای گرد کردن (به بالا یا به پایین) همیشه به یک شکل نیست. با توجه به ماهیت عدد، ممکن است گرد کردن به پایین یا به بالا، دارای خطای کمتر یا بیشتری باشد.

با در نظر گرفتن نکته قبل، به نظر می‌رسد که بهتر است روشی برای گرد کردن اعداد انتخاب کنیم که به طور متوسط خطای کمتری نسبت به روش‌های دیگر داشته باشد.

گرد کردن اعداد

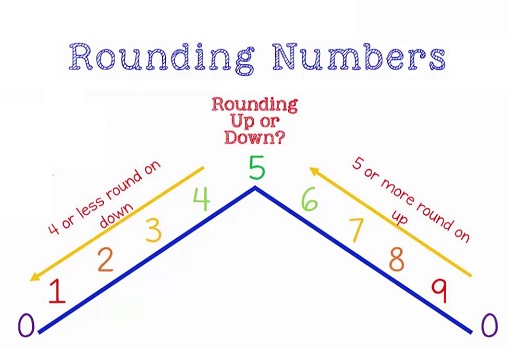
اگر دنباله ارقام ۰ تا 10 را در نظر بگیرید، میانه آن‌ها (با توجه به فرد بودن تعداد ارقام)، برابر با ۵ خواهد بود.

$$\large 0 , 1 , 2 , 3, 4 , \color{red} { \huge 5} \large, 6 , 7 , 8 , 9 , 10$$

به این ترتیب ارقام مربوط به مثلا یکان اعداد به طور متوسط در ۵۰ درصد مواقع بزرگتر یا برابر با ۵ و ۵۰ درصد دیگر کمتر از ۵ هستند. البته توجه دارید که در اینجا ۱۰ به معنی عددی با یک واحد بزرگتر برای رقم یکان در نظر گرفته شده است. بنابراین اگر به طور شانسی عمل گرد کردن را از بین «گردن کردن به بالا» و «گرد کردن به پایین» انتخاب کنیم، درست مثل یک است که هر یک از ارقامی که قرار است حذف شوند را با ۵ مقایسه کرده و در صورتی که بزرگتر یا مساوی با ۵ باشند، به بالا و در غیر این صورت به پایین گرد کنیم. بهتر است برای روشن شدن موضوع به مثال‌هایی در این زمینه بپردازیم.

نکته: گاهی برای اینکه عدد را به بالا یا به پایین گرد کنند، از یک پدیده شانسی، مثل پرتاب سکه، استفاده کرده و هرگاه سکه شیر باشد، رو به بالا و اگر سکه خط بیاید، عدد را رو به پایین گرد می‌کنند.

مثال 7

باز هم عدد ۱۲۳٫۸۶ را در نظر می‌گیریم. اگر بخواهیم آن را به عدد صحیح گرد کنیم، به رقمی که از آن رقم به بعد باید حذف شود، توجه می‌کنیم. اگر این رقم برابر با بزرگتر از ۵ بود، گرد کردن را به بالا در نظر می‌گیریم. بنابراین از آنجایی که رقم ۸ (مربوط به اولین رقم اعشاری) بزرگتر از ۵ است، حاصل گرد کردن عدد ۱۲۳٫۸۶ به عدد صحیح برابر است با 124.

به این ترتیب می‌توانیم قاعده زیر را برای گردن کردن در نظر بگیریم.

قاعده گرد کردن: گردن کردن یک عدد، یعنی مقایسه اولین رقم حذفی با ۵. در صورتی که این رقم از ۵ بزرگتر یا مساوی باشد، از آن رقم به بعد (به سمت راست) را حذف کرده و به رقم قبل از آن (رقم سمت چپ) یک واحد اضافه می‌کنیم (برای اعداد مثبت، گرد به بالا).  در صورتی که رقم حذفی از ۵ کوچکتر باشد، از آن رقم به سمت راست را حذف کرده و چیزی به رقم سمت چپ، اضافه نخواهیم کرد (برای اعداد مثبت، گرد به پایین).

مثال ۸

این بار فرض کنید می‌خواهیم عدد ۱۲۳٫۸۶- را با یک رقم اعشار گرد کنیم. چون این عدد منفی است، باید با دقت از قاعده گرد کردن استفاده کنیم. همانطور که گفته شد، قرار است عدد گرده شده، یک رقم اعشار داشته باشد، پس رقم 6 را باید حذف کنیم. چون این عدد از ۵ بزرگتر است، آن را حذف کرده و یک واحد به رقم سمت چپ اضافه می‌کنیم. در نتیجه حاصل گرد کردن عدد ۱۲۳٫۸۶- برابر است با ۱۲۳٫9- و تقریب یا خطای گرد کردن نیز ۰٫۰۴ است.

$$\large | -123.86 \; - (-123.9) | = 0.04$$

ولی اگر به جای اضافه کردن یک واحد به ۸، فقط رقم ۶ را حذف می‌کردیم، حاصل گرد کردن، عددی به صورت ۱۲۳٫۸- می‌شد که خطای گرد کردن آن برابر با ۰٫۰۶ بود.

گرد کردن به عدد زوج

با توجه به قواعدی که برای گرد کردن اعداد بیان کردیم، می‌توانیم یک عدد را به نزدیک‌ترین عدد زوج (Even) نیز گرد کنیم. البته توجه داشته باشید که این کار بیشتر برای اعداد طبیعی (صحیح و مثبت) یا «اعداد اعشاری مثبت» به کار می‌رود.

قاعده گرد کردن به نزدیک‌ترین عدد زوج: رقم مورد نظر برای حذف شدن اگر بزرگتر از ۵ باشد، حاصل گرد کردن، کوچکترین عدد زوجی است که از عدد مورد نظر بزرگتر است. در غیر این صورت بزرگترین عدد زوجی که از عدد مورد نظر کوچکتر است، نتیجه گرد کردن خواهد بود.

نکته: عدد زوج، عددی است که یکان آن یکی از ارقام ۰، ۲، ۴، ۶ یا ۸ باشد. به بیان دیگر عددی که به ۲ بخش پذیر باشد، عدد زوج است.

مثال ۹

نتیجه گرد کردن عدد ۱۲۳٫۸۶ به عدد زوج برابر است با ۱۲۴، زیرا لازم است اولین رقم اعشار را حذف کرده و نزدیک‌ترین عدد زوج را انتخاب کنیم، چون رقم ۸ بزرگتر از ۵ است، پس از حذف آن، یک واحد به یکان اضافه کرده تا حاصل ۱۲۴ شود. از آنجایی که این عدد زوج است، عمل گرد کردن متوقف می‌شود. واضح است که خطای این میزان گرد کردن برابر است با ۰٫۰۴.

گرد کردن به عدد فرد

شیوه گرد کردن به عدد فرد درست به مانند عدد زوج است با این تفاوت که نزدیک‌ترین عدد از بین اعداد فرد انتخاب می‌شود.

قاعده گرد کردن به نزدیک‌ترین عدد فرد: رقم مورد نظر برای حذف شدن اگر بزرگتر از ۵ باشد، حاصل گرد کردن، کوچکترین عدد فردی است که از عدد مورد نظر بزرگتر است. در غیر این صورت بزرگترین عدد فردی که از عدد مورد نظر کوچکتر است، نتیجه گرد کردن خواهد بود.

به یاد داشته باشید که عدد فرد، عددی است که زوج نباشد. پس می‌توان یکان اعداد فرد را یکی از ارقام ۱،۳ ،۵، ۷ و ۹ در نظر گرفت.

مثال ۱۰

به نظر شما، حاصل گرد کردن عدد ۱۲۴ به نزدیک‌ترین عدد فرد چیست؟ ۱۲۳ و ۱۲۵ نزدیکترین اعداد صحیح فرد به ۱۲۴ هستند. کدامیک از آن‌ها را به عنوان نتیجه گرد کردن انتخاب کنیم. همانطور که مشخص است، خطای گرد کردن برای هر یک از این دو عدد نسبت به ۱۲۴، یک واحد است، پس فرقی نمی‌کند که کدام یک را انتخاب کنید. هر کدام از اعداد ۱۲۳ یا ۱۲۵ به یک میزان خطای گرد کردن داشته و در محاسبات بعد خطای یکسانی ایجاد می‌کنند. البته ۱۲۳ یک تقریب نقصانی و ۱۲۵ یک نقریب اضافه ایجاد می‌کنند.

نکته: در نرم‌افزار اکسل، همیشه عمل گرد کردن به عدد زوج یا فرد، عددی را نتیجه می‌دهد که از عدد اصلی بزرگتر است.

گرد کردن به نزدیک‌ترین عدد صحیح مضرب ۱۰

اغلب در محاسبات مالی، لازم است که اعداد را به نزدیک‌ترین مضرب ۱۰ گرد کنیم. البته این که عمل گرد کردن به بالا صورت گیرد یا به پایین، بحثی است که در اینجا به آن خواهیم پرداخت. ابتدا با یک مثال آغاز می‌کنیم.

مثال ۱۱

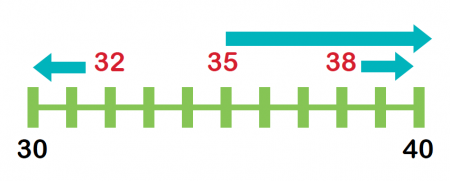
عدد ۱۲۳٫۸۶ را می‌خواهیم به نزدیک‌ترین مضرب ۱۰ گرد کنیم. از آنجایی که مضرب‌های ۱۰ در یکانشان، رقم ۰ را دارند، پس باید یکان عدد ۱۲۳٫۸۶ را گرد کنیم. از آنجایی که رقم ۳، کمتر از ۵ است، عمل گرد کردن به پایین صورت گرفته و حاصل برابر با ۱۲۰ خواهد شد. خطای گرد کردن در اینجا برابر با ۳٫۸۶ است.

در نظر داشته باشید که اگر قرار بود عدد را به مضرب ۱۰۰ یا 10² گرد کنیم، رقم دهگان (یا رقم دوم از سمت راست) باید گرد می‌شد. مشخص است که توان ۱۰ یعنی ۲، نشانگر مکان رقمی است که باید گرد شود. در این صورت حاصل عمل گرد کردن ۱۲۳٫۸۶ به صورت مضربی از ۱۰۰ برابر با عدد ۱۰۰ می‌بود و خطای گرد کردن نیز برابر با ۲۳٫۸۶ بدست می‌آمد.

به این ترتیب می‌توان قاعده زیر را برای گرد کردن عدد به مضرب‌های صحیح از ۱۰ معرفی کرد.

قاعده گرد کردن به مضرب‌های ۱۰: درجه توان ۱۰ را در نظر می‌گیریم. مطابق با این عدد، رقم مطابق با این درجه را عدد گرد می‌کنیم و ارقام سمت راست را حذف و به جایشان صفر می‌گذاریم.

گرد کردن به نزدیک‌ترین عدد صحیح مضرب عدد خاص

در تراکنش‌های مالی اغلب دوست داریم که اعداد و ارقام محاسبه شده برحسب، واحدهای سر راست اسکناس یا سکه مشخص شوند. اگر قرار است پرداخت حقوق کارکنان براساس اسکناس صورت گیرد، بهتر است که حقوق به نزدیک‌ترین مضربی از ۵۰ تومان که اسکناسش در دسترس قرار دارد، گرد شده و پرداخت‌ها با حداقل اسکناس ۵۰ تومانی همراه باشد. به این ترتیب می‌خواهیم حقوق را به نزدیک‌ترین عدد صحیح مضرب عدد ۵۰ گرد کنیم. باز هم با یک مثال موضوع گرد کردن اعداد را پی خواهیم گرفت.

فیلم مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

مثال ۱۲

فرض کنید لازم است مقدار حقوق ۱۲۳ را به نزدیک‌ترین مضرب ۵۰ گرد کنیم. البته با توجه به اینکه دوست داریم همیشه کارکنان از شرکت طلب‌کار باشند، شیوه گرد کردن به پایین را انتخاب کرده‌ایم. ابتدا ۱۲۳ را به ۵۰ تقسیم می‌کنیم.

$$\large 123 \div 50 = 2.46$$

حاصل این تقسیم را به پایین گرد کرده و نزدیک‌ترین عدد صحیح را استخراج می‌کنیم. واضح است که مقدار حاصل برابر با ۲ خواهد بود. حال ۲ را در ۵۰ ضرب می‌کنیم و به مقدار ۱۰۰ خواهیم رسید. در نتیجه حاصل گرد کردن عدد ۱۲۳ بر حسب مضربی از ۵۰، برابر با ۱۰۰ خواهد بود.

توجه داشته باشید که در حالت کلی وقتی عمل تقسیم انجام می‌شود، بهتر است از گرد کردن ساده (مقایسه با ۵ و اجرای گرد کردن به پایین یا بالا) استفاده کرده و نتیجه را در مقسوم علیه مورد نظر، ضرب کنیم. برای مثال حاصل گرد کردن عدد ۹ بر مضربی از ۲ برابر با ۱۰ خواهد بود زیرا:

$$\large 9 \div 2 = 4.5$$

حال با گرد کردن 4٫5 به نزدیک‌ترین عدد صحیح، به مقدار ۵ رسیده که حاصل ضرب آن در ۲ برابر با ۱۰ خواهد بود. پس گرد شده عدد ۹ نسبت به مضربی از ۲ به شکل ۱۰ محاسبه و نمایش داده می‌شود. همین کار را برای اعداد اعشاری نیز می‌توان انجام داد. برای مثال حاصل گرد کردن عدد ۰٫۲3 برحسب مضربی از ۰٫۰۵ برابر است با 0٫۲۵، زیرا:

$$\large 0.23 \div 0.05 = 5.4$$

با گرد کردن ۵٫۴، حاصل برابر با ۵ شده و در نتیجه ضرب آن در ۰٫۰۵، مقدار ۰٫۲۵ را نشان می‌دهد.

خلاصه و جمع‌بندی

در این نوشتار از مجله فرادرس با چند شیوه و روش گرد کردن اعداد آشنا شدیم. بیشتر نرم‌افزارهای محاسباتی، توابع و روش‌هایی برای گرد کردن اعداد دارند که قادرند مقادیر را به بالا، پایین، به نزدیک‌ترین عدد صحیح یا مضربی از یک عدد دیگر گرد کنند. برای مثال توابع برای انجام این کار در اکسل وجود دارند که در اینجا هر یک از آن‌ها را به صورت فهرست‌وار معرفی می‌کنیم.

• تابع Rounddown - گرد کردن به پایین
• تابع Roundup- گرد کردن به بالا
• تابع Round- گرد کردن با مقایسه با ۵
• تابع Even - گرد کردن به عدد زوج
• تابع Odd- گردن کردن به عدد فرد
• تابع Mround- گرد کردن به یک مضرب خاص

اطلاعات بیشتر در زمینه نحوه به کارگیری این توابع در اکسل را در نوشتار گرد کردن عدد اعشاری در اکسل پیدا خواهید کرد. البته توجه داشته باشید که توابع Odd و Even در اکسل، همیشه عدد را به بالا گرد می‌کنند. یعنی به نزدیک‌ترین عدد فرد یا زوجی که از خود عدد بزرگتر هستند، عمل گرد کردن صورت می‌گیرد.