جمع و تفریق ذهنی – از صفر تا صد

امروزه برای محاسبه جمع، تفریق، ضرب و تقسیم اعداد از ماشین حساب استفاده می‌کنیم. در اغلب تلفن‌های همراه نیز برنامه ماشین حساب وجود دارد که می‌توانیم از آن‌ها برای انجام محاسبه مجموع خرید روزانه، باقی پول خرید و غیره استفاده کنیم. ولی اگر تلفن همراه‌تان در دسترس‌تان نباشد چه کاری باید کرد؟ تنها راه باقی‌مانده، استفاده از محاسبات بخصوص جمع و تفریق ذهنی است. ولی شاید این کار وقت‌گیر بوده و احتیاج به کاغذ و خودکار داشته باشد؛ نگران نباشید. روش‌هایی وجود دارند که محاسبات جمع و تفریق ذهنی را برایتان، راحت و ساده می‌کنند. در این نوشتار به جمع و تفریق ذهنی و سریع اعداد صحیح می‌پردازیم و از رمزهای آن آگاه خواهیم شد.

در مطلبی که در ادامه آمده است با استفاده از مجموعه اعداد صحیح، محاسبات را انجام می‌دهیم. برای آشنایی بیشتر با این اعداد می‌توانید مطالب اعداد صحیح — به زبان ساده و اعداد طبیعی — به زبان ساده را بخوانید. همچنین خواندن متن جمع در اکسل --- به زبان ساده و تفریق در اکسل --- به زبان ساده نیز خالی از لطف نیست.

جمع و تفریق ذهنی

شاید به نظرتان افرادی که جمع و تفریق ذهنی را انجام می‌دهند، نابغه باشند. ولی آن‌ها به کمک روش‌هایی ساده، این عملیات را به سرعت انجام می‌دهند.

همانطور که در عنوان این مطلب دیده می‌شود، هدف در جمع و تفریق ذهنی پیدا کردن روش‌هایی است که به کمک آن‌ها بتوانیم به راحتی و البته با سرعت، نتایج جمع و تفریق ذهنی دو عدد را پیدا کنیم. با توجه به روابطی که بین دو عدد وجود دارد، روش‌های مختلفی برای جمع‌ و تفریق ذهنی آن‌ها ایجاد شده است. البته همیشه عمل جمع یا تفریق به صورت عادی، نتیجه بخش خواهد بود ولی در اینجا به دنبال سرعت بخشیدن به عمل جمع و تفریق ذهنی هستیم.

نکته: به این موضوع توجه داشته باشید که عملیاتی که در ادامه مرتبط با جمع و تفریق ذهنی بوده و مورد بحث قرار می‌گیرد از خاصیت‌های جابجایی، شرکت‌پذیری و پخشی عملگرهای ریاضی استفاده می‌کنند تا انجام محاسبات را به شکلی درآوردند که برای ذهن ما ساده‌تر باشد.

جمع ذهنی

برای شروع کار به جمع‌کردن ذهنی اعداد می‌پردازیم. ابتدا برای جمع ساده برای اعداد یک رقمی و سپس نوع خاصی از اعداد دو رقمی روش‌هایی را معرفی کرده، سپس برای جمع اعداد مختلف، راه‌کارهایی را ارائه می‌کنیم.

جمع اعداد زیبا

زوج اعداد زیر را در نظر بگیرید:

۱ و 9

2 و ۸

۳ و ۷

۴ و ۶

۵ و ۵

همانطور که می‌بینید مجموع هر یک از این زوج‌ها برابر با مقدار ۱۰ است. هر چند این موضوع را همه می‌دانند ولی استفاده از آن برای انجام عملیات جمع و تفریق بسیار کارساز است. اجازه دهید این زوج اعداد را به عنوان اعداد زیبا نام‌گذاری کنیم. به این ترتیب هر گاه هنگام جمع کردن به این زوج‌ها برخوردید، می‌دانید که مجموعشان برابر با ۱۰ است.

مجموع اعداد دو رقمی مقلوب

یکی از نکات جالبی که در جمع‌کردن اعداد دو رقمی خاص به کار می‌رود، جمع اعداد مقلوب است. البته برای تفریق اعداد مقلوب دو رقمی نیز قاعده‌ای وجود دارد که در ادامه با آن‌ها آشنا خواهیم شد. ابتدا تعریف دو عدد مقلوب را ارائه می‌دهیم.

دو عدد را مقلوب یکدیگر می‌گویند، اگر یکی از آن‌ها با تغییر ترتیب ارقام دیگری ساخته شده باشد. برای مثال عدد ۱۴ , 41 مقلوب یکدیگر هستند، زیرا ترتیب قرارگیری ۴ و ۱ در چهارده و چهل و یک، عکس یکدیگر است. اعداد ۵۳ و ۳۵، ۹۸ و ۸۹ نیز از این گونه هستند.

واضح است که نتیجه جمع یکان این گونه اعداد با مجموع ده‌گان آن‌ها برابر است. به این ترتیب کافی است که مجموع ارقام یکان این دو عدد را با یکدیگر جمع کرده و در عدد ۱۱ ضرب کنیم تا حاصل جمع آن دو عدد حاصل شود.

برای مثال جمع ۱۴ و ۴۱ یا ۵۳ و ۳۵ و همچنین ۹۸ و ۸۹ به شکل زیر بدست می‌آید.

$$\large 1 \, 4 + \overbrace{ 4 \; 1 }^{ 4 + 1 = 5 } = 5 \times 11 = 55$$

$$\large 5 \, 3 + \overbrace{ 3 \; 5 }^{ 3 + 5 = 8 } = 8 \times 11 = 88$$

$$\large 9 \, 8 + \overbrace{ 8 \; 9 }^{ 8 + 9 = 17 } = 17 \times 11 = 187$$

در ادامه روش‌های عدد مبنا، شکست و تجزیه، دزدی رقم و روش ترکیبی را فرا گرفته و برای جمع کردن به کار می‌گیریم.

روش عدد مبنا

در تکنیک عدد مبنا، یک مقدار عددی که محاسبات براساس آن ساده‌تر است را به عنوان معیار قرار داده و سعی می‌کنیم یک یا هر دو عدد مربوط به جمع را برحسب آن بنویسیم. معمولا عدد مبنا می‌تواند ۱۰ یا ۵ باشد. انتخاب این عدد براساس دانشی است که برای جمع کردن اعداد داریم. برای مثال ممکن است فردی جمع اعداد را با ۸ به خوبی انجام دهد. بنابراین بهتر است عدد مبنا را ۸ انتخاب کند.

نکته: این روش برای زمانی که یکی از عددهای جمع، تک رقمی است، با سرعت عمل می‌کند.

در ادامه با استفاده از مثال‌هایی با تکنیک عدد مبنا آشنا خواهیم شد. توجه داشته باشید که عدد مبنا را مقداری انتخاب کنید که با استفاده از تجزیه یکی از اعداد و جمع با عدد دیگر به آن می‌رسید.

مثال ۱

فرض کنید قرار است دو عدد ۱۵ و ۸ را با یکدیگر جمع کنیم.

$$\large 15 + 8$$

واضح است که این جمع از ۲۰ بزرگتر است. بنابراین ۲۰ را مبنا قرار می‌دهیم. مقدار ۸ را به ۵ و ۳ تفکیک می‌کنیم، زیرا ۱۵ برای آنکه به ۲۰ تبدیل شود، احتیاج به ۵ واحد دارد. پس خواهیم داشت:

$$\large 15 + \underbrace{ 5 + 3 }_8$$

به این ترتیب مجموع ۱۵ و ۵ که برابر با ۲۰ است را در ذهن قرار می‌دهیم.

$$\large \underbrace{20}_{ 15 + 5 } + 3$$

به این ترتیب جمع را به صورت زیر تکمیل می‌کنیم.

$$\large 20 +  3 = 23$$

مثال ۲

حاصل مجموع ۶۳ و ۹ را با تکنیک عدد مبنا به صورت زیر در ذهن حل می‌کنیم. از آنجایی که مجموع این دو عدد از ۷۰ بزرگتر است، عدد مبنا را ۷۰ (که مضربی از ۱۰ است) انتخاب می‌کنیم.

$$\large 63 + 9$$

حال مراحل زیر را طی می‌کنیم. مشخص است که برای رسیدن به ۷۰ باید ۷ واحد به ۶۳ اضافه شده و ۷ واحد از ۹ نیز کاسته شود.

$$\large 63 + \underbrace{ 7 + 2 }_9$$

در این مرحله، عدد مبنا را بدست می‌آوریم.

$$\large \underbrace{70}_{ 63 + 7 } + 2$$

در نهایت، نتیجه را با ۲ جمع می‌کنیم.

$$\large 70 + 2 = 72$$

مثال ۳

۱۱۷ و ۶ را با تکنیک عدد مبنا با یکدیگر جمع بسته و مراحل را نشان می‌دهیم.

$$\large 117 + 6$$

از آنجایی که این جمع از ۱۲۰ بزرگتر است، مبنا را ۱۲۰ انتخاب می‌کنیم. از طرفی وجود صفر در رقم یکان آن، جمع با اعداد بعدی را برای عدد مبنا ساده‌تر می‌کند.

پس خواهیم داشت:

$$\large 117 + \underbrace{ 3 + 3 }_6$$

حال محاسبات را ادامه می‌دهیم.

$$\large 117 + 3 + 3 = 120 + 3 = 123$$

روش شکست و تجزیه

در این روش با شکستن یک عدد و تجزیه آن به عوامل دیگر، عمل جمع را ساده‌تر کرده و محاسبات را به صورت ذهنی انجام می‌دهیم. به این ترتیب اعداد را برمبنای رقم‌های یکان، دهگان و ... جمع می‌کنیم.

برای آشنایی با این تکنیک نیز از چند مثال استفاده می‌کنیم.

مثال 4

حاصل جمع ۱۲ و ۸۸ را به کمک روش شکست و تجزیه بدست می‌آوریم. ۱۲ و ۸۸ را بر حسب یکان و دهگانشان جداگانه می‌نویسم. به این ترتیب خواهیم داشت:

$$\large \underbrace{ 10 + 2 }_{12} + \underbrace{ 80 + 8 }_{88}$$

حال، یکان‌ها را جداگانه و دهگان‌ها را هم جداگانه جمع می‌کنیم، زیرا می‌دانیم که جمع دارای خاصیت شرکت‌پذیری است. واضح است که در اینجا از جمع اعداد زیبا که در بالا به آن اشاره کردیم، استفاده خواهیم کرد. پس داریم:

$$\large \underbrace{10 + 80}_{90} + \underbrace{ 2 + 8 }_{10}$$

از آنجایی که ۸+۲ شامل یک ده بر یک خواهد بود، باید به دهگان یک واحد اضافه کنیم. پس حاصل جمع برابر است با ۱۰۰.

$$\large 80 + 10 + 10 = 100$$

نکته: می‌توانستیم برای جمع این دو عدد از شکست و تجزیه به صورت دیگری هم استفاده کنیم. راه حل دیگر در ادامه آورده شده است.

$$\large 12 + 88 = 10 + 2 + 88 = 10 + 90 = 100$$

حتی این کار را با تجزیه ۸۸ نیز می‌توان انجام داد:

$$\large 12 + 88 = 12 + 8 + 80 = 20 + 80 = 100$$

بنابراین ممکن است به هر شکلی که برایتان راحت‌تر است، شکست و تجزیه را انجام دهید ولی همیشه نتیجه جمع یکسان خواهد بود.

مثال ۵

حاصل جمع 36 و ۷۲ را با روش شکست و تجزیه انجام می‌دهیم. ابتدا اعداد را به تفکیک یکان و دهگان می‌نویسیم.

$$\large \underbrace{30 + 6}_{36} + \underbrace{ 70 + 2 }_{72}$$

به کمک خاصیت شرکت‌پذیری عمل جمع می‌نویسیم، مشخص است که بخش اول شامل جمع دهگان‌ها و بخش دوم جمع یکان‌ها را محاسبه کرده است.

$$\large \underbrace{ 30 + 70 } + \underbrace{ 6 + 2 }$$

به این ترتیب حاصل جمع برابر با ۱۰۸ خواهد بود.

$$\large \underbrace{100}_{ 30 + 70 } + \underbrace{8}_{6 + 2}= 100 + 8 = 108$$

روش دزدی رقم

در این تکنیک، برای جمع دو عدد، یک واحد از یکی از اعداد دزدیده شده و به عدد دیگر داده می‌شود. به این ترتیب به اصطلاح می‌گویند «یکی از اعداد گدا و دیگری ثروتمند می‌شود».

باز هم برای روشن‌تر شدن موضوع از چند مثال استفاده می‌کنیم. البته توجه داشته باشید که این روش را برای زمانی که اعداد دو رقمی بوده و رقم یکان به ۰ یا ۵ نزدیک باشد، به خوبی عمل می‌کند.

مثال 6

حاصل جمع دو عدد ۴۹ و ۸۶ را به کمک روش دزدی رقم، انجام می‌دهیم. از آنجایی که یکان ۸۶ یعنی رقم ۶ به مقدار ۵ نزدیک است و از طرفی در ۴۹، رقم یکان با اضافه شدن یک واحد به صفر تبدیل می‌شود از تکنیک دزدی رقم استفاده می‌کنیم.

$$\large 86 - 1 = 85 \\ \large 49 + 1 = 50$$

پس می‌توان نوشت:

$$\large 86 + 49 = 86 - 1 + 49 + 1$$

زیرا اضافه و کم کردن یک مقدار ثابت از حاصل جمع، نتیجه را تغییر نمی‌دهد. به این ترتیب خواهیم داشت:

$$\large 86+49 = 86 - 1 + 49 + 1= 85 + 50 = 135$$

مثال ۷

حاصل جمع ۵۲ و ۶۸ را هم به شیوه دزدی رقم انجام می‌دهیم ولی اینجا به نظر می‌رسد که رقم دزدیده شده از ۵۲ باید ۲ باشد.

$$\large 52 - 2 = 50 \\ \large 68 + 2 = 70$$

پس می‌توان نوشت:

$$\large 68 + 52 = 68 + 2 + 52 - 2 = 70 + 50 = 120$$

نکته: البته این جمع را با تکنیک شکست و تجزیه و استفاده از اعداد زیبا نیز می‌توان انجام داد.

$$\large 68 + 52 = 60 + 8 + 50 + 2 = 110 + 10 = 120$$

روش ترکیبی

در روش ترکیبی، از تکنیک‌های قبلی به صورت ترکیبی برای محاسبه جمع دو عدد استفاده می‌کنیم. به این ترتیب ممکن است در یک گام از روش دزدی رقم و در گام بعدی از روش شکست و تجزیه استفاده کنیم. باز هم در اینجا برای روشن شدن موضوع از چند مثال استفاده می‌کنیم.

نکته: اغلب برای جمع اعداد چند رقمی از روش ترکیبی استفاده می‌کنیم.

مثال 8

حاصل جمع دو عدد 462 و 379 را با ترکیب کردن چندین روش ذهنی، بدست می‌آوریم.

ابتدا با تکنیک شکست و تجزیه، صدگان و دهگان‌ها را جدا می‌کنیم.

$$\large \underbrace{400 + 62}_{462} + \underbrace{300 + 79}_{379}$$

با استفاده از خاصیت شرکت‌پذیری و جابجایی جمع، ابتدا صدگان‌ها و سپس دهگان‌ها را جمع می‌کنیم.

$$\large 400 + 300 + 62 + 79 = 700 + 62 + 79$$

در این مرحله برای جمع 62 و ۷۹ نیز از دزدی رقم استفاده می‌کنیم.

$$\large 400 + 300 + 62 + 79 = 700 + 62-1 + 79 + 1 = \\ \large 700 + 61 + 80$$

به سادگی می‌توانیم با جابجایی و شکست و تجزیه بنویسیم:

$$\large 700 + 61 + 80 = 780 + 61 = 780 + 60 + 1$$

این بار از تکنیک عدد مبنا کمک گرفته و حاصل جمع 60 با 780 را بدست می‌آوریم. واضح است که حاصل جمع ۶۰ و ۷۸۰ از ۸۰۰ بزرگتر است، پس عدد مبنا را ۸۰۰ می‌گیریم.

$$\large \underbrace{800}_{780 + 20} + \underbrace{40}_{ 60 - 20 } + 1 = 841$$

تفریق ذهنی

در این قسمت به روش‌هایی اشاره می‌کنیم که عمل تفریق را برایتان ساده‌تر کرده و امکان انجام محاسبات ذهنی را می‌دهد و با کمی تکرار و تمرین کردن این تکنیک‌ها، سرعت انجام محاسباتتان بیشتر خواهد شد. ابتدا به مانند روش جمع اعداد مقلوب دو رقمی، به شیوه تفریق آن‌ها می‌پردازیم.

اگر قرار باشد اعداد مقلوب دو رقمی را از هم کسر کنیم کافی است تفاصل رقم یکان و دهگان یکی از آن‌ها را در ۹ ضرب کنیم. به این ترتیب تفاضل آن دو عدد محاسبه می‌شود.

باز هم به همان اعداد مقلوبی که در جمع به آن‌ها پرداختیم، توجه می‌کنیم. البته تفاضل را به شکلی محاسبه می‌کنیم که همیشه رقم کوچکتر را از رقم بزرگتر کم می‌کنیم تا نتیجه تفاضل، منفی نباشد.

$$\large 4 \, 1 - \overbrace{ 1 \; 4 }^{ 4 - 1 = 3 } = 3 \times 9 = 27$$

$$\large 5 \, 3 - \overbrace{ 3 \; 5 }^{ 5 - 3 = 2 } = 2 \times 9 = 18$$

$$\large 9 \, 8 - \overbrace{ 8 \; 9 }^{ 9 - 8 = 1 } = 1 \times 9 = 9$$

نکته: می‌توانیم قدرمطلق تفاضل هر دو رقم را هم مبنا قرار داده و در عدد ۹ ضرب کنیم.

اغلب روش‌هایی که برای جمع سریع و ذهنی گفته شد، برای تفریق نیز قابل استفاده است. بنابراین با ذکر چند مثال، این تکنیک‌ها را برای تفریق هم به کار می‌بریم.

مثال 9

تفاضل ۹ از ۱۵ چقدر است؟ در اینجا از تکنیک عدد مبنا استفاده می‌کنیم. در واقع قرار است حاصل رابطه زیر را پیدا کنیم.

$$\large 15-9$$

واضح است که این تفاضل از ۱۰ کوچکتر است. در این روش، مقدار ۱۰ را مبنا قرار می‌دهیم زیرا نزدیک‌ترین عدد مضرب ۱۰ است که از تفاضل این دو عدد بزرگتر است و محاسبات را به صورت زیر در نظر می‌گیریم.

$$\large 15 - (\overbrace{5 + ?}^9)$$

واضح است که به جای علامت ? باید مقدار ۴ را انتخاب کرد. در نتیجه رابطه بالا را به صورت زیر می‌نویسیم.

$$\large 15 - (\overbrace{5 + 4}^{9}) = 15- 5 - 4 = 10 - 4 = 6$$

مثال ۱۰

برای محاسبه 3-22 نیز به صورت زیر عمل می‌کنیم. می‌دانیم که این تفاضل از ۱۰ بزرگتر است، پس مبنا را 20 در نظر می‌گیریم زیرا نزدیکترین مقدار به نتیجه تفاضل است که مضربی از ۱۰ خواهد بود. در نتیجه خواهیم داشت:

$$\large 22- (\overbrace{2 + ?}^3)$$

حال با توجه به اینکه مقدار ? برابر با 1 خواهد بود، می‌نویسیم:

$$\large 22 - (\overbrace{2 + 1}^{3}) = 22 - 2 - 1 = 20 - 1 = 19$$

شمارش به بالا

یکی دیگر از شیوه‌های معمول برای محاسبه تفریق، شمارش به بالا است. این امر به این معنی است که برای تعیین حاصل تفریق، از عدد دوم تفریق شروع کرده و عمل شمارش را انجام می‌دهیم تا به عدد اول برسیم. تعداد شمارش‌های صورت گرفته، حاصل تفریق است.

مثال ۱۱

حاصل تفاضل ۹ از ۱۵ با تکنیک شمارش به بالا به صورت زیر انجام می‌شود.

$$\large 15 - 9$$

از عدد ۹ شروع می‌کنیم و به آن یک واحد اضافه می‌کنیم و این عمل را آنقدر تکرار می‌کنیم تا به ۱۵ برسیم. تعداد تکرارهای طی شده یا گام‌ها، حاصل تفریق است.

$$\large \;\;\; 9 + \color{blue}{1} = 10, \;\; 10 + \color{blue}{1} = 11, \;\; 11 + \color{blue}{1} = 12 , \\ \large 12 + \color{blue}{1} = 13, \;\; 13 + \color{blue}{1} = 14, \;\; 14 + \color{blue}{1} = 15$$

مشخص است که باید تعداد ۱ ها را بشماریم تا نتیجه تفریق بدست آید. بنابراین مقدار تفریق برابر است با ۶.

$$\large 15 - 9 = 6$$

مثال ۱۲

مقدار ۵۹-۱۲۷ را به کمک تکنیک شمارش به بالا انجام می‌دهیم. همانطور که گفته شد از ۵۹ شمارش را آغاز می‌کنیم تا به ۱۲۷ برسیم. در گام اول داریم:

$$\large 59 + \color{blue}{1} = 60$$

از آنجایی که برای رسیدن به ۱۲۰ کافی است ۶۰ بار عمل جمع با ۱ را تکرار کنیم، پس می‌نویسیم:

$$\large 59 + \color{blue}{1} = 60, \;\; 60 + \color{blue}{60} = 120, \;\; 120 + \overbrace{\color{blue}{1 + 1 + 1 + 1 + 1 + 1 + 1 }}^7 = 127$$

در نتیجه حاصل این تفریق برابر است با 7+1+60=68.

مثال ۱۳

حاصل 328-572 با طی کردن گام‌های زیر با روش شمارش به بالا، مشخص می‌شود. در گام اول با شمارش از ۳۲۸ شروع کرده تا به ۳۳۰ برسیم.

$$\large 328 + \color{blue}{2} = 330$$

حالا شمارش به بالا را تا ۴۰۰ ادامه می‌دهیم.

$$\large 330 + \overbrace{\color{blue}{ 1 + 1 + \cdots + 1 }}^{70} = 400$$

از طرفی برای رسیدن به ۵۰۰ نیز باید یک جهش ۱۰۰ تایی با گام‌هایی به طول ۱ داشته باشیم.

$$\large 400 + \overbrace{\color{blue}{1 + 1 + \cdots + 1}}^{100} = 500$$

در انتها نیز برای رسیدن به 572 باید ۷۲ گام دیگر برداریم.

$$\large 500 + \overbrace{\color{blue}{ 1 + 1 + \cdots + 1 }}^{72} = 572$$

در نتیجه حاصل تفاضل برابر است با 72+100+70+2=244.

تفاضل به عنوان فاصله دو عدد روی محور اعداد

اگر محور اعداد را برای نمایش اعداد صحیح به کار ببریم، مشخص است که تفاضل دو عدد به معنی فاصله بین آن دو در نظر گرفته می‌شود.

در نتیجه با توجه به مثال بالا باید فاصله بین ۳۲۸ تا ۷۷۲ شمارش و محاسبه شود. با توجه به محور، مشخص است که این فاصله شامل زیر فاصله‌های دیگری است که به آسانی در تصویر‌های زیر قابل مشاهده هستند.

گام اول:

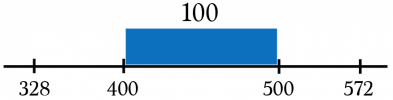
گام دوم:

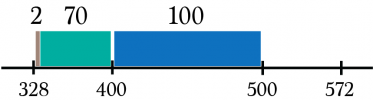
گام سوم:

با جمع کردن این فاصله‌ها، مقدار تفاضل بدست خواهد آمد.

$$\large \color{blue}{ 2 + 70 + 100 + 70 + 2 } = 140 + 100 + 4 = 244$$

خلاصه و جمع‌بندی

در این نوشتار به بررسی نحوه محاسبه جمع و تفریق ذهنی و شیوه‌های مختلف آن پرداختیم. البته روش‌های ترکیبی که به صورت ابتکاری به کار می‌روند، می‌توانند راهکار مناسبی برای انجام این گونه محاسبات باشند. جمع و تفریق اعداد مقلوب دو رقمی نیز در این بین مورد بحث قرار گرفت. هر چند شاید جمع و تفریق ذهنی اعداد در نگاه اول به نظر مشکل برسد ولی با کمی تمرین و تلاش، قواعد را فرا می‌گیرید و می‌توانید با سرعت زیاد و بدون اشتباه، جمع و تفریق ذهنی را انجام دهید و در نظر دیگران به یک فرد بسیار باهوش تبدیل شوید.