کنترل بهینه در متلب — از صفر تا صد

در آموزش‌های قبلی مجله فرادرس، با جایابی قطب برای طراحی کنترل‌کننده آشنا شدیم. دیدیم که جایابی قطب روشی است که در آن، یک ماتریس بهره محاسبه می‌شود و با استفاده از فیدبک حالت، قطب‌های سیستم حلقه‌بسته در جای مطلوب قرار می‌گیرند. البته، انتخاب قطب‌های مطلوب سیستم را به صورت تقریبی و تجربی انجام دادیم. اما، با استفاده از کنترل بهینه می‌توانیم قطب‌ها را به صورت بهینه انتخاب کنیم. در این آموزش درباره کنترل بهینه و پیاده‌سازی آن در متلب بحث خواهیم کرد.

مقدمه

برای مثال، سیستم انتگرال‌گیر دوگانه $$\ddot{x} = u$$ را در نظر بگیرید. فرض کنید دو کنترل‌کننده با ماتریس‌های بهره بزرگ و کوچک طراحی کرده‌ایم. شکل‌های زیر پاسخ سیستم را برای این دو کنترل‌کننده نشان می‌دهند. همان‌طور که در این شکل‌ها مشخص است، هرچه بهره بزرگ‌تر باشد، خطا زودتر به صفر میل می‌کند و البته سیگنال کنترل نیز بزرگتر خواهد بود. بنابراین، با انتخاب یک ماتریس بهره مناسب، طراح کنترل می‌تواند بین مقادیر بالا و پایین، نقطه بهینه‌ای را انتخاب کند که در آن، خطا با سرعت مناسب و سیگنال کنترلی معقولی به صفر میل کند. برنامه متلب زیر، مربوط به رسم دو نمودار است. می‌توانید مقادیر بهره را تغییر دهید و نتایج را با هم مقایسه کنید.

فیلم آموزش کنترل بهینه – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

1clc
2close all
3clear all
4
5K_high = [100 40];
6K_low = [40 .8];
7x0= [10;0];
8
9t = 0:0.01:10;
10K = K_high;
11sys_fun = @(t,x)[x(2); -K*x];
12[t X_high] = ode45(sys_fun,t,x0);
13K = K_low;
14sys_fun = @(t,x)[x(2); -K*x];
15[t X_low] = ode45(sys_fun,t,x0);
16
17figure;
18plot(t,K_high*X_high',t,K_low*X_low')
19legend('Control: High K','Control: Low K')
20figure;
21plot(t,X_high(:,1),t,X_low(:,1))
22legend('Position: High K','Position: Low K')

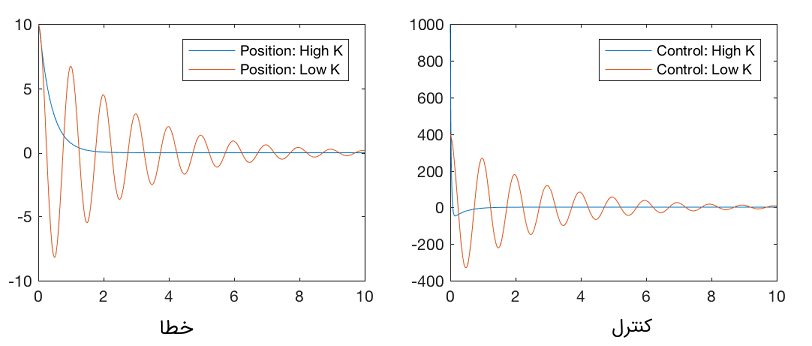
در ادامه، با فرمول‌بندی کنترل بهینه و رگولاتور خطی درجه دوم آشنا می‌شویم.

فرمول‌بندی کنترل بهینه

کنترل بهینه را می‌توان با در نظر گرفتن موارد مختلف فرمول‌بندی کرد. در ادامه برخی موارد را بیان می‌کنیم.

فیلم آموزش کنترل مدرن و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

حالت کلی: بدون قید زمان، مسیر و کنترل

در این بخش، کلی‌ترین حالت کنترل بهینه را در نظر می‌گیریم که در آن، هیچ محدودیت یا قیدی برای مسیر، سیگنال کنترل یا زمان رسیدن به هدف وجود ندارد. سیستم زیر را در نظر بگیرید:

$$\large \dot { X } = f ( x , u ) ,$$

که در آن، شرایط اولیه $$X(0) = X_0$$ است. می‌خواهیم قانون کنترل $$u$$ را به گونه‌ای بیابیم که تابع هزینه (Cost Function) زیر کمینه شود:

$$\large J ( u ) = \Phi ( X _ f ) + \int _ { t = 0 } ^ { t _ f } L ( t , X , u ) d t .$$

بنابراین، مسئله کنترل بهینه را می‌توان به صورت زیر فرمول‌بندی کرد:‌

$$\large Minimize ~ J ( u )$$

مشروط به:

$$\large \dot{X} = f(X,u)$$    و    $$\large X(0) = X_0$$

استخراج شرایط لازم بهینه‌سازی

اولین گام در به دست آوردن قانون کنترل، استخراج شرایط لازمی است که کنترل‌کننده در آن‌ها صدق کند. برای انجام این کار، ابتدا معادله دینامیکی سیستم را به صورت یک تابع خطا به انتگرال‌ده اضافه می‌کنیم:

$$\large J ( u ) = \Phi ( X _ f ) + \int _ { t = 0 } ^ { t _ f } \left ( L (t , X , u ) + \lambda ^ T ( f ( x , u ) - \dot { x } ) \right ) d t .$$

هامیلتونی (Hamiltonian) یا همیلتونین $$H( x,u,\lambda )$$ را به صورت زیر تعریف می‌کنیم:

$$\large H ( x , u , \lambda ) = L ( t , X , u ) + \lambda ^ T f( x , u ) ,$$

اکنون مسئله کنترل بهینه را می‌توان به صورت زیر نوشت:

$$\large J ( u ) = \Phi ( X _ f ) - \int _ { t = 0 } ^ { t _ f } \left ( H ( x , u , \lambda ) - \lambda ^ T \dot { x } \right ) d t .$$

با استفاده از انتگرال‌گیری جزء به جزء، برای عبارت دوم داریم:

$$\large \int _ { t = 0 } ^ { t _ f } \lambda ^ T \dot { x } d t = \lambda ^ T ( X _ f - X _ 0 ) - \int _ { t = 0 } ^ { t _ f } \dot { \lambda } ^ T x d t .$$

در نتیجه، تابع هزینه به صورت زیر در خواهد آمد:

$$\large J ( u ) = \Phi ( X _ f ) - \lambda ^ T ( X _ f - X _ 0 ) + \int _ { t = 0 } ^ { t _ f } \left ( H ( x , u , \lambda ) + \dot { \lambda } ^ T x \right ) d t .$$

در ادامه، تغییرات $$J$$ را با توجه به تغییرات $$\delta u$$ ورودی کنترل محاسبه می‌کنیم. از آنجایی که متغیرهای حالت به ورودی کنترل وابسته‌اند، تغییرات تلاش کنترلی منجر به تغییرات حالت می‌شود که آن را با $$\delta x$$ نشان می‌دهیم. تغییرات تابع هزینه نسبت به $$u$$ برابر است با:

$$\large \delta J = \left . \left ( \frac { \partial \Phi } { \partial X } - \lambda ^ T \right ) \delta x \right | _ { t _ f , X _ f } + \int _ { t = 0 } ^ { t _ f } \left [ \left ( \frac { \partial H }{ \partial X } + \dot { \lambda } ^ T \right ) \delta x + \left ( \frac { \partial H } { \partial u } \right ) \delta u \right ] d t .$$

از آنجایی که $$\lambda (t)$$ اختیاری هستند، می‌توانیم آن‌ها را به گونه‌ای انتخاب کنیم که $$\delta J = 0$$‌ برقرار باشد و برای این انتخاب $$\lambda (t)$$، یک جواب بهینه خواهیم داشت. شرایط بهینگی به صورت زیر است:

$$\large \dot { \lambda } = - \frac { \partial H } { \partial X } ^ T ,$$

که شرایط مقدار نهایی آن برابر است با:

$$\large \lambda _ f = \left . \frac { \partial \Phi } { \partial X } ^ T \right | _ { t _ f , X _ f } .$$

معادلات $$\lambda$$ به عنوان معادلات کمک‌حالت (Costate Equations) نیز شناخته می‌شوند.

قانون کنترل با شرایط مانا داده می‌شود:

$$\large \frac { \partial H } { \partial u } = 0$$

تغییرات زمانی حالت‌ها نیز از رابطه زیر به دست می‌آید:

$$\large \dot{X} = f(X,u)$$    و    $$\large X(0) = X_0$$

معادلات حالت و کمک‌حالت شرایط لازم را مشخص می‌کنند که قانون کنترل باید در آن صدق کند. شرایط مرزی متغیرهای حالت نیز در شرایط اولیه و شرایط مرزی متغیرهای کمک‌حالت در زمان نهایی تعریف می‌شوند. حل این مسئله با مقدار مرزی دو نقطه‌ای بسیار دشوار است و برای حل آن روش‌های عددی متعددی وجود دارد. در حالت خاصی که سیستم خطی است، می‌توانیم متغیرهای کمک‌حالت را به عنوان تابعی از متغیرهای حالت و تابع هزینه را به صورت یک تابع درجه دوم از حالت‌ها و کنترل بنویسیم. در این صورت می‌توان یک جواب عمومی وابسته به حالت را به دست آورد.

رگولاتور خطی و پیوسته‌ زمان درجه دوم با زمان محدود

در سیستم‌های خطی، می‌توانیم با بیان کمک‌حالت به عنوان تابعی خطی از حالت‌ها، یک نمایش مستقل از حالت برای آن بنویسیم. همچنین، در سیستم‌های خطی، تابع هزینه یک تابع درجه دوم از حالت و کنترل است. این فرم به عنوان کنترل یا رگولاتور مرتبه دوم خطی (Linear Quadratic Regulator) یا LQR نامیده می‌شود. در LQR، قانون کنترل را به گونه‌ای محاسبه می‌کنیم که تابع هزینه درجه دوم زیر کمینه شود:

$$\large J ( u ) = \frac { 1 } { 2 } X _ f ^ T S X _ f + \frac { 1 }{ 2 } \int _ { t = 0 } ^ { t _ f } ( X ^ T Q X + u ^ T R u ) d t .$$

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

که در آن، $$Q$$ یک ماتریس معین نیمه‌مثبت است و هزینه یا ارزش انحراف متغیرها از صفر را نشان می‌دهد، $$R$$ یک ماتریس معین مثبت است و هزینه کنترل را نشان می‌دهد، و $$S$$ یک ماتریس معین مثبت است که خطا از مقدار مطلوب نهایی (در اینجا، صفر) را جریمه می‌کند. ماتریس‌های $$Q$$ و $$R$$ به صورت یک ماتریس قطری انتخاب می‌شوند. مقادیر بزرگ $$Q$$ خطای مسیر و مقادیر بزرگ $$R$$ کنترل را جریمه می‌کنند. بنابراین، استفاده از این فرمول‌بندی، کار طراح کنترل را برای تشخیص قطب‌های سیستم آسان کرده و تمرکز او را به تنظیم وزن‌های مربوط به هزینه کنترل و خطای ردیابی محدود می‌کند. یک فرایند طراحی کنترل معمولی با تغییر وزن‌های خطای ردیابی و هزینه یا تلاش کنترلی سر و کار دارد تا پاسخ مناسب به دست آید. موارد زیر، توصیه‌هایی برای انتخاب مقادیر مناسب $$Q$$ و $$R$$ هستند. نُرم (Norm) یک سنجش برای مقادیر ماتریس‌ها است و نرم $$L_2$$ (جذر مجموع مربع درایه‌ها) برای هدف ما گزینه مناسبی است. برای انتخاب ماتریس‌های $$R$$ و $$Q$$ موارد زیر کارساز خواهند بود:

1. برای $$\text{norm} ( R ) \gg \text {norm} ( Q )$$، تلاش کنترلی با جریمه سنگینی روبه‌رو خواهد بود، و کنترل‌کننده حاصل از این انتخاب دیرتر خطا را صفر خواهد کرد.
2. برای $$\text{norm} ( Q ) \gg \text {norm} ( R )$$، هزینه خطای ردیابی بالا بوده و خطا سریعاً به صفر خواهد رسید.
3. می‌توان $$R$$ را به گونه‌ای انتخاب کرد که درایه‌های قطری آن مقادیر متفاوتی داشته باشند. در این حالت، کنترل متناظر با مقدار قطری بزرگ‌تر، کمتر استفاده خواهد شد.
4. می‌توان $$Q$$ را به گونه‌ای انتخاب کرد که درایه‌های قطری آن مقادیر متفاوتی داشته باشند. در این حالت، حالت‌های متناظر با مقادیر قطری بزرگ‌تر، سریع‌تر به صفر میل می‌کنند.

اکنون می‌توان مسئله کنترل بهینه را به صورت زیر نوشت:

$$\large Minimize ~ J (u)$$

مشروط به

$$\large \dot{X} = AX + Bu$$    و    $$X(0) = X_0$$

با تعریف همیلتونین به صورت زیر:

$$\large H ( X , u , \lambda ) = \frac { 1 } {2 } \left ( X ^ T Q X + u ^ T R u \right ) + \lambda ^ T ( A X + B u )$$

شرایط بهینگی به صورت زیر خواهد بود:

$$\large \begin {align*} \dot { \lambda } & = - A ^ T \lambda + Q X , \\ 0 & = B ^ T \lambda + R u , \\ \dot { X } & = A X + B u . \end {align*}$$

با شرایط مرزی زیر:

$$\large X(0) = X_0$$    و    $$\large \lambda_f = S X_f$$

انتظار داریم قانون کنترل تابعی از حالت‌ها باشد. بنابراین، $$\lambda = P X$$‌ را در نظر می‌گیریم. با مشتق‌گیری از این رابطه، داریم:

$$\large \dot{ \lambda } = \dot { P } X + P \dot { X }$$

حال این رابطه را در معادله زیر جایگذاری می‌کنیم:

$$\large \dot { \lambda }= - A ^ T \lambda - Q X ,$$

با توجه به روابط $$\lambda = PX$$ و $$\dot{X} = AX + Bu$$، داریم:

$$\large \dot { P } X + P ( A X + B u ) = - A ^ T P X - Q X .$$

با انتخاب $$u= - R ^ { - 1 } B ^ T \lambda = - R ^ { - 1 } B ^ T P X$$، داریم:

$$\dot { P } X + P ( A X - B R ^ { - 1 } B ^ T P X ) = - A ^ T P X - Q X .$$

با کمی عملیات جابه‌جایی در عبارات معادله بالا، می‌توان نوشت:

$$\large \dot { P } X = - P A X - A ^ T P X + P B R ^ { - 1 } B ^ T P X - Q X .$$

معادله بالا برای همه مقادیر $$X$$ برقرار است، بنابراین:

$$\large - \dot { P } = P A + A ^ T P - P B R ^ { - 1 } B ^ T P + Q  .$$

شرایط مرزی نیز $$P_f = S$$ است. معادله بالا، معادله ریکاتی (Riccati Equation) نامیده می‌شود و جواب آن همان جواب بهینه است.

توجه کنید که در مشتق‌گیری فرض کردیم زمان نهایی ثابت است. اگر زمان نهایی یک پارامتر قابل تغییر باشد، آنگاه شرط $$\frac{\partial \Phi}{\partial t} + H_f = 0$$ نیز اضافه می‌شود.

برنامه متلب مربوط به این نوع کنترل بهینه سیستم انتگرال‌گیر دوگانه به صورت زیر است. به مقادیر عددی تعریف شده در برنامه دقت کنید و برای درک بهتر از طراحی کنترل، آن‌ها را تغییر داده و نتایج را با هم مقایسه کنید.

1clc
2close all
3clear all 
4
5t_f = 5;
6dt = 0.001;
7P_f= 100*eye(2);
8Q = .0001*eye(2);
9R = 1;
10A = [0 1;0 0];
11B = [0 ;1];
12P0 =P_f;
13
14
15
16% Vectors
17
18N = t_f/dt+1;
19
20
21% add t_dis array 
22t_dis = linspace( 0, t_f, N );
23t_res = linspace(t_f, 0, N );
24
25t_dis = 0:dt:t_f;
26t_res = t_f:-dt:0;
27
28P_all_res(:,length(t_res))= P_f(:);
29for i = length(t_res):-1:2
30    P =reshape(P_all_res(:,i),size(A));
31    dPdt = -(A.'*P + P*A - P*B*B.'*P + Q); 
32    
33    P = P - dt*(dPdt);
34    P_all_res(:,i-1)= P(:);
35end
36P_all_res = P_all_res';
37
38
39X0=[10;0];
40X_eul(:,1) = X0;
41
42for i = 2:length(t_dis)
43    P_eul = reshape(P_all_res(i-1,:),size(A));
44    U_eul(:,i-1) = -inv(R)*B'*P_eul*X_eul(:,i-1);
45    X_eul(:,i) = X_eul(:,i-1) + dt* (A*X_eul(:,i-1) + B*U_eul(:,i-1) );  
46end
47
48figure
49plot(t_dis(1:end-1),U_eul)
50ylabel('control')
51xlabel('time')
52
53figure;
54plot(t_dis,X_eul)
55ylabel('states')
56xlabel('time')
57legend('Position','Velocity')

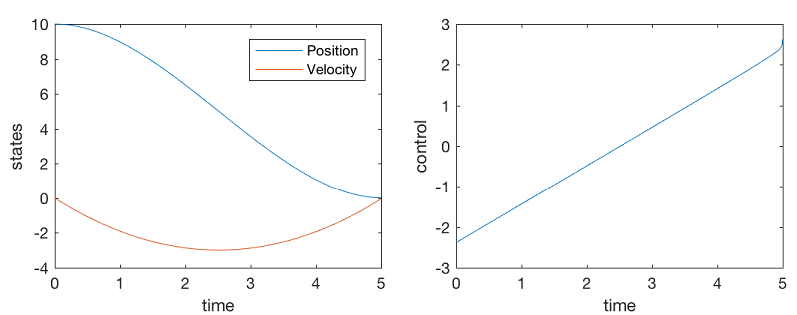
همان‌طور که می‌بینیم اندازه سیگنال کنترل کمتر از ۵ واحد است. هیچ‌ کنترل‌کننده PID نمی‌تواند این عملکرد را به نمایش بگذارد و سیگنال کنترل آن به ۱۰۰ ثانیه زمان نیاز خواهد داشت.

رگولاتور خطی و پیوسته‌ زمان درجه دوم با زمان نامحدود

تابع هزینه در حالتی که زمان به بی‌نهایت میل می‌کند، به صورت زیر است:‌

$$\large J ( u ) = \frac { 1 } { 2 } \int _ { t = 0 } ^ { \infty } ( X ^ T Q X + u ^ T R u ) d t .$$

در شرایط حالت ماندگار $$\dot{P} = 0$$ است. بنابراین، معادله ریکاتی به صورت زیر در می‌آید:

$$\large 0 = P A + A ^ T P - P B R ^ { - 1 } B ^ T P + Q .$$

معادله بالا یک معادله جبری است. حل این معادله را می‌توان با استفاده از تابع "care" در متلب به دست آورد. برنامه زیر نشان می‌دهد که چگونه تابع "care" مقادیر بهره بهینه را محاسبه و تابع بالا را کمینه می‌کند.

1K_high = [100 40];
2K_low = [40 .8];
3x0= [10;0];
4
5
6M_a = rank(ctrb(A,B));
7t = 0:0.01:10;
8
9P = care(A,B,Q,R);
10K = inv(R)*B'*P;
11K_opt = K
12sys_fun = @(t,x)[x(2); -K_opt*x];
13[t X_opt] = ode45(sys_fun,t,x0);
14
15K = K_high;
16sys_fun = @(t,x)[x(2); -K_high*x];
17[t X_high] = ode45(sys_fun,t,x0);
18
19K = K_low;
20sys_fun = @(t,x)[x(2); -K_low*x];
21[t X_low] = ode45(sys_fun,t,x0);
22
23figure;
24plot(t,-K_high*X_high',t,-K_low*X_low',t,-K_opt*X_opt',t_dis(1:end-1),U_eul)
25%legend('Control: High K','Control: Low K','Control: Opt K','Position: Fixed time')
26figure;
27plot(t,X_high(:,1),t,X_low(:,1),t,X_opt(:,1),t_dis,X_eul(1,:))
28legend('Position: High K','Position: Low K','Position: Opt K','Position: Fixed time')

شکل‌های حاصل از اجرای برنامه بالا، به صورت زیر هستند.

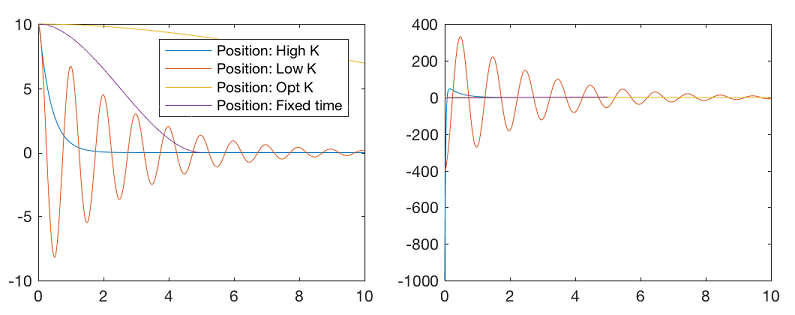
نمودارهای بالا نشان می‌دهند که کنترل‌کننده بهینه خطاها را سریع‌تر به سمت صفر می‌برد و به مقدار سیگنال کنترل کمتری نیاز دارد. کنترل‌کننده بهینه را می‌توان برای سیستم‌های گسسته نیز طراحی کرد. در آموزش‌های بعدی درباره این موضوع بحث خواهیم کرد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سیستم کنترل حلقه باز — به زبان ساده
• تقلب نامه (Cheat Sheet) کنترل خطی
• پاسخ سیستم مرتبه دوم — از صفر تا صد

^^