همنهشتی مثلث ها در هندسه – به زبان ساده
در هندسه (Geometry)، دو شکل را همنهشت (congruent) میگویند اگر دارای شکل و اندازه یکسانی باشند. چرخش و دوران چنین شکلهایی باعث از بین رفتن همریختی و همنهشتی آنها نمیشود. در این بین همنهشتی مثلث در هندسه از اهمیت بیشتری برخوردار است. زیرا بسیار از اشکال را میتوان به مثلثهای مختلف افراز کرد. در این نوشتار به بررسی همنهشتی مثلث ها در هندسه خواهیم پرداخت و با شیوههای تعیین آن آشنا خواهیم شد. در انتها نیز برای تشخیص همنهشتی چند ضلعی ها، روشی ارائه خواهیم کرد.


برای آشنایی بیشتر با اشکال هندسی بهتر است نوشتار چهار ضلعی ها — به زبان ساده و آشنایی با چند وجهی ها — به زبان ساده را مطالعه کنید. همچنین خواندن مطلب آشنایی با تبدیلات هندسی — به زبان ساده و حرکت انتقالی در ریاضیات — به زبان ساده نیز خالی از لطف نیست.
همنهشتی مثلث ها در هندسه
همانطور که در ابتدای متن اشاره شد، همریختی و همشکلی دو شکل هندسی به معنی آن است که بتوانیم آنها را مشابه یکدیگر تشخیص دهیم. در این بین برای بیان ریاضی و ایجاد قوانین همنهشتی از تعریف و قضیههایی استفاده میشود که در ادامه به آنها اشاره خواهیم کرد.
به طور رسمی میگوییم دو شکل همنهشت هستند اگر مجموعه نقاط هر یک از آنها بوسیله یک تبدیل متقارن (Ismoetry) به مجموعه نقاط دیگری تبدیل شود. منظور از تبدیل متقارن، محاسباتی است که اندازه یا زوایای شکل را تغییر نداده و صرفا باعث دوران یا جابجایی نقاط شود.
در تصویر زیر چهار مثلث ترسیم شده است. دو مثلث سمت چپ با یکدیگر همنهشت هستند. مثلث سوم با مثلثهای اول و دوم مشابه (Similar) است، ولی همنهشت نیست. از طرفی مشخص است که مثلث چهارم هم در اندازه اضلاع و هم زاویه با مثلثهای دیگر متفاوت است.
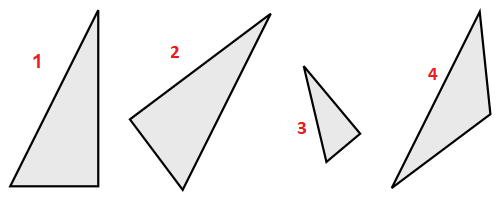
به بیان دیگر میتوان گفت که اشکالی که بوسیله دوران، انعکاس یا جابجایی بر یکدیگر منطبق میشوند، همنهشت هستند. در تصویر ۱ مشخص است که مثلث دوم را با مقداری دوران (Rotation) و ایجاد تصویر انعکاسی (Reflection) و همچنین جابجایی (Translation) میتوانیم بر شکل اول منطبق کنیم. در ادامه هر یک از این تبدیلات را که باعث همنهشتی مثلث ها در هندسه خواهند شد، مرور خواهیم کرد.
تبدیل دوران (Rotation Transformation)
دوران یا چرخش، یک حرکت دایرهای از یک تصویر در اطراف یک مرکز یا نقطه مرکزی است. در تصویر زیر دوران یک شکل را مشاهده میکنید. همانطور که مشخص است فاصله بین نقطهها و قالب شکلها در کل، تغییری نیافته است ولی نحوه نمایش شکل تغییر کرده است.
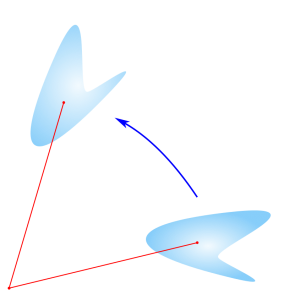
تبدیل جابجایی (Translation Transformation)
تبدیل جابجایی، عملی است که طی آن تمامی نقطهها به اندازهای ثابت در جهتی خاص انتقال داده میشوند. تصویر زیر نشانگر یک تبدیل جابجایی است که طی یک محور مستقیم نقاط تغییر یافتهاند.

تبدیل انعکاسی (Reflection Transformation)
یک تصویر تبدیل یافته توسط یک تبدیل انعکاسی (بازتابی)، تصویر آینه آن در محور یا صفحه انعکاس است. همانطور که در تصویر زیر دیده میشود، خطوط قرمز رنگ به عنوان محور در نظر گرفته شده و شکل قرمز، حول خط پایین، انعکاس داشته تا شکل سبز رنگ را پدیده آورد. همچنین انعکاس دوباره این شکل روی محور موازی با محور اولیه شکل آبی رنگ را پدیده آورده است که با شکل قرمز رنگ معادل است. این امر نشان میدهد استفاده از دوبار تبدیل انعکاسی روی یک شکل یکسان، دوباره شکل اولیه را بازسازی میکند.

تعریف همنهشتی هندسی
در هندسه بعضی اوقات اصطلاح رابطه همنهشتی با رابطه برابری یکسان در نظر گرفته میشود. در ادامه این موارد را بازگو میکنیم.
- دو قطعه خط همنهشت هستند، اگر دارای طول برابر باشند.
- دو زاویه همنهشت هستند، اگر اندازه برابر داشته باشند.
- دو دایره همنهشت هستند، اگر دارای قطر یکسانی باشند.
به این ترتیب میتوان گفت دو شکل در هندسه همنهشت هستند اگر همه اجزای آنها برابر یا همنهشت باشند. این برابری و همنهشتی نه تنها برای زاویهها و اضلاع دو شکل باید صدق کند، بلکه قطرها، محیط و مساحت آنها نیز باید یکسان باشد. از طرفی تشابه، میتواند به دو شکل مربوط باشد که مشابه بوده ولی یکسان و برابر نباشند. همانطور که در تصویر ۱، شکل اول و سوم مشابه یکدیگرند ولی برابر نیستند. این امر نشان میدهد که میتوان همنهشتی را برای دو شکل مشابه در صورتی در نظر گرفت که همه اجزای آنها نیز برابر باشند.
همنهشتی مثلث ها
دو مثلث را همنهشت گویند، اگر اضلاع متناظر آنها دارای طولهای یکسان و زاویه متناظر نیز با اندازههای برابر باشند. اگر مثلث ABC همنهشت با مثلث DEF باشد، از نماد زیر استفاده خواهیم کرد.
در بسیاری از حالتها، به جای بررسی همنهشتی همه اجزای مثلثها، کافی است بعضی از خصوصیات اصلی آنها را مورد بررسی قرار دهیم. در فضای اقلیدسی میتوان همنهشتی مثلثها را به یکی از صورتهای زیر نشان داد.
- دو ضلع و زاویه بین (Side-Angle-Side) یا SAS: اگر دو ضلع از مثلثی دارای طولهای یکسانی باشند و زاویه بین آن دو نیز در دو مثلث یکسان باشد، آن دو مثلث را همنهشت مینامند.
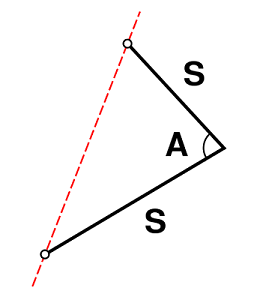
- سه ضلع (Side-Side-Side) یا SSS: اگر سه ضلع از مثلثی با سه ضلع از مثلثی دیگر برابر باشند، آن دو مثلث همنهشت خواهند بود.
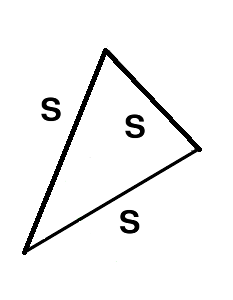
- دو زاویه و ضلع بین (Angle-Side-Angle) یا ASA: اگر دو زاویه و ضلع بین آنها در دو مثلث با یکدیگر برابر باشند، آن دو مثلث را همنشهت مینامند.
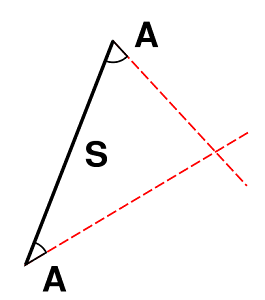
- دو زاویه و یک ضلع (Angle-Anlge-Side) یا AAS: فرض کنید دو زاویه از دو مثلث با یکدیگر برابرند. اگر ضلعی، غیر از ضلع میان این دو زاویه نیز با ضلع متناظرش در مثلث دیگر برابر باشد، آنگاه دو مثلث همنهشت خواهند بود.
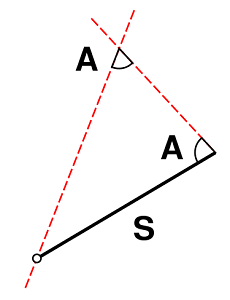
نکته: از آنجایی که با برابر بودن دو زاویه در بین دو مثلث میتوان نتیجه گرفت که سه زاویه مثلثها نیز برابرند، میتوان وضعیت AAS و ASA را یکسان در نظر گرفت. زیرا مجموع زاویههای هر مثلث برابر با ۱۸۰ درجه است، در نتیجه به راحتی با یکسان بودن دو زاویه در بین دو مثلث، به برابری زاویه سوم هم پی خواهیم برد. در چنین حالتی گاهی از اصطلاح AAcorrS استفاده میشود که در برخی موارد به آن همنهشتی با دو زاویه و یک ضلع نیز میگویند.
- وتر و یک ضلع در مثلث قائمالزاویه (Right-angle-Hypotenuse-Side) یا RHS: با توجه به اینکه در یک مثلث قائمالزاویه، زاویه ۹۰ درجه وجود دارد، با فرض برابری وتر و یک ضلع دیگر میتوان براساس قانون فیثاغورس (Pythagorean Theorem)، نتیجه گرفت که ضلع سوم آنها نیز برابر است و در نتیجه طبق وضعیت SSS، دو مثلث همنهشت خواهند بود. از دیگر حالتهای همنهشتی مثلثهای قائمالزاویه میتوان به حالت دو ضلع، یک ضلع و یک زاویه حاده، یک ضلع و ارتفاع وارد بر وتر اشاره کرد.
ولی باید توجه داشت که وجود رابطه تساوی سه زاویه در بین دو مثلث (Angle-Angle-Angle) یا AAA یا دو ضلع و یک زاویه به تنهایی (Side-Side-Angle) یا SSA، نمیتواند همنهشتی دو مثلث را نتیجه دهد.
نکته: برابری سه زاویه در بین دو مثلث، باعث همنهشتی نمیشود. در تصویر ۱، مثلث شماره ۱ با مثلث شماره ۳ مشابه بوده ولی همنهشت نیستند. زیرا سه زوایه در هر دو شکل برابر هستند ولی اضلاع متناظر در این مثلثها با یکدیگر برابر نیست.
اصل همنهشتی مثلث ها در هندسه
طبق تعریف همنهشتی، شرط کافی برای آنکه دو شکل همنهشت باشند، آن است که اجزای آنها همنهشت باشند. عکس این حالت برای مثلثها نیز برقرار است. به این معنی که اگر دو مثلث همنهشت باشند، آنگاه تمامی اجزای آنها نیز همنهشت خواهند بود.
به این اصل گاهی همنهشتی جزئی مثلث (CPCTC) یا Corresponding Parts of Congruent Triangles are Congruent میگویند.
این گزاره به صورت ریاضی به شکل زیر نوشته میشود.
آنگاه
همنهشتیهای بالا بخصوص زمانی که به همنهشتی اجزای مثلثهای برابر احتیاج داریم، ضروری است. برای مثال اگر بتوانیم نشان دهیم که دو مثلث بنابر حالت SSS، همنهشت هستند، میتوانیم بنا به همنهشتی، برابری زاویههای هر دو مثلث را هم نتیجه بگیریم.
نکته: در اشکال چند وجهی (Polygon) این قضیه را میتوان به کار برد. به این معنی که با همنهشتی بین دو چند وجهی، میتوان به همنهشتی اجزای آنها رسید.
همنهشتی در چند وجهی یا چند ضلعیها
برای اینکه دو چند ضلعی همنهشت باشند، باید در اولین گام، دارای تعداد اضلاع برابر باشند. به این ترتیب هر دو چند ضلعی دارای تعداد رئوس و قطرهای برابر هستند. دو چند ضلعی که دارای تعداد اضلاع برابر باشند، به شرطی همنهشت هستند که دارای توالی ضلعها و زاویههای یکسان باشند (چه ساعتگرد چه پادساعتگرد). این امر به این معنی است که مثلا ضلعی که در هر دو شکل دارای طولی برابر با ۵ است، به زاویههای یکسانی نیز منتهی شود.
چند ضلعیهای همنهشت را بوسیله مراحل زیر میتوانید شناسایی کنید:
- اول، راسهای مربوط به دو شکل را مطابقت داده و برچسب بزنید.
- دوم، یک خط از راس یکی از شکلها به سمت راس مرتبط با شکل دیگر بکشید. شکل اول را توسط این بردار تبدیل کنید تا این دو راس بر یکدیگر منطبق شوند.
- سوم، شکل تبدیل یافته را در حول راس همسان دوران دهید تا ضلعهای متناظر، بر یکدیگر منطبق شوند.
- چهارم، شکل چرخش یافته را حول ضلعی که منطبق کردهاید، منعکس (بازتاب) دهید تا زمانی که همه اضلاع و در نتیجه هر دو شکل بر هم منطبق شوند.
اگر پس از طی کردن این مراحل، شکلها بر یکدیگر منطبق نشدند، آن دو چند ضلعی، همنهشت نیستند.
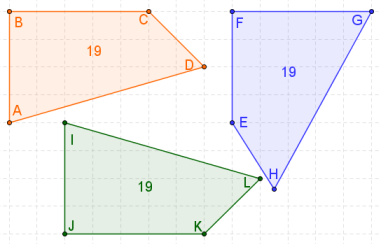
در تصویر ۲، سه شکل چهار ضلعی مشخص شده است که همگی همنهشت هستند. در تصویر مشخص است که همگی اشکال، محیطی یکسان و برابر با ۱۹ دارند. فرض کنید میخواهیم شکل نارنجی رنگ را بر شکل سبز رنگ منطبق کرده و نتیجه بگیریم که این دو شکل همنهشت هستند. مراحل زیر را طی خواهیم کرد.
- نقطه را بر نقطه منطبق میکنیم. زیرا هر دو زاویه یکسان (قائمه یا ۹۰ درجه) دارند.
- ضلع را میتوان بر ضلع منطبق کرد.
- با چرخش آینهای (انعکاسی) تصویر نارنجی رنگ، حول ضلع ، دو تصویر منطبق خواهند شد. به این ترتیب واضح میشود که شکل نارنجی و سبز رنگ همنهشت هستند.
این عملیات را میتوان برای شکل آبی رنگ نیز انجام داد و نتیجه گرفت که این چند ضلعی، با چند ضلعی نارنجی رنگ همنهشت است. پس مشخص است که چند ضلعی سبز رنگ هم با چند ضلعی آبی رنگ همنهشت خواهد بود. از این امر میتوان نتیجه گرفت که رابطه همنهشتی، یک رابطه تراگذری (Transitive) است.
خلاصه و جمعبندی
در این نوشتار به بررسی همنهشتی (Congruent) و همنهشتی مثلثها در هندسه پرداختیم. قضیههای مرتبط با این موضوع برای مثلثها نیز بیان شد. همانطور که مشاهده کردید، عکس قضیه همنهشتی هم برای مثلث برقرار است.
آزمون همنهشتی مثلث ها
۱. شرط اصلی برای همنهشتی دو شکل هندسی چیست و این شرط چه تفاوتی با تشابه دارد؟
تشابه و همنهشتی هر دو فقط بر اساس جابجایی تعریف میشوند.
دو شکل فقط نیاز به داشتن زاویههای برابر دارند.
همنهشتی یعنی دو شکل فقط دارای مساحت برابر باشند.
دو شکل باید تمام اجزای متناظرشان برابر باشد تا همنهشت باشند.
در همنهشتی، باید همه اجزای متناظر دو شکل مانند ضلعها و زاویهها کاملا باهم برابر باشند، اما در تشابه فقط لازم است زوایا برابر و اضلاع متناسب باشند نه الزاما برابر.
۲. کدام نوع تبدیل هندسی تنها موقعیت یک شکل را تغییر میدهد و باعث حفظ اندازه و شکل آن میشود؟
دوران موجب تغییر موقعیت و حفظ شکل میشود.
جابجایی تنها جای شکل را بدون تغییر اندازه عوض میکند.
کوچکنمایی یا بزرگنمایی اندازه شکل را تغییر میدهد.
انعکاس فقط شکل را نسبت به محور برمیگرداند.
در تبدیل جابجایی، فقط مکان شکل در صفحه تغییر میکند بدون اینکه تغییری در اندازه یا شکل آن ایجاد شود. «دوران» نیز اندازه و شکل را حفظ میکند اما شکل را حول یک نقطه معین میچرخاند. «انعکاس» شکل را نسبت به یک محور برمیگرداند که ممکن است سمت راست و چپ آن عوض شود ولی باز هم اندازه حفظ میشود.
۳. در بررسی همنهشتی مثلثها، کدام شرایط معتبر بوده و چرا حالتی مانند AAA منجر به همنهشتی نمیشود؟
شرایط SAS، SSS، ASA، AAS و RHS برای اثبات همنهشتی کافی هستند و AAA فقط برابری زاویهها را میدهد.
همه حالات بالا از جمله AAA و SSA تضمین همنهشتی مثلثها را دارند.
فقط SSA و AAA کافی هستند و شرایط دیگر همیشه قابل استفاده نیستند.
تمام حالات گفته شده فقط مشابهت را نشان میدهند، نه همنهشتی.
شرایطی مانند SAS، SSS، ASA، AAS و RHS زمانی قابل اعتمادند که میخواهیم همنهشتی دو مثلث را در هندسه اثبات کنیم. علت ناکافی بودن AAA آن است که این وضعیت صرفا برابری زوایا را نشان داده و الزاما اندازه اضلاع را تضمین نمیکند، بنابراین ممکن است مثلثها فقط مشابه باشند. SSA نیز به دلیل عدم پیوند زاویه با اضلاع مشخص، همیشه منجر به همنهشتی نمیشود. پس فقط شرایطی که دادههای دقیق درباره اضلاع و زوایا ارائه دهند، برای اثبات همنهشتی معتبر خواهند بود.
۴. اگر دو چندضلعی با تعداد اضلاع یکسان پس از انجام جابهجایی، دوران و انعکاس بر یکدیگر منطبق نشوند، کدام نتیجه صحیح است؟
چندضلعیها مشابهاند و فقط اندازههایشان فرق میکند.
امکان دارد با تغییر ترتیب برچسبگذاری، همنهشتی به دست آید.
ممکن است چندضلعیها با اضافه کردن یک زاویه جدید همنهشت شوند.
چندضلعیها همنهشت نیستند زیرا هر تبدیل مجاز امتحان شده و انطباق کامل به دست نیامده است.
زمانی که با انجام تمام تبدیلات مجاز همنهشتی، یعنی جابهجایی، دوران و انعکاس، هنوز دو چندضلعی روی هم منطبق نمیشوند، نتیجه میگیریم که آنها همنهشت نیستند، چون همه مراحل لازم برای برابری دقیق اضلاع و زوایا طی شده است.













ممنونم مطالب تون عالی بود
فقط می تونم بگم عالی
سلام عزیزم
فرض شما اینه که یک زاویه معلوم داریم و دو زاویه دیگه مجهوله حالا با کشیدن ضلع مجاور زاویه و مشخص کردن زاویه ای که داریم ضلع معلوم دوم روبروی زاویه معلومه خب حالا ضلع دوم می کشیم چون زاویه مجاورش مجهوله به دلخواه زاویه تند میکشیم حالا با اتصال ضلع سوم مثلث مشخص میشه ولی بیا برگردیم عقب اگه زاویه مجهول رو یه زاویه باز بکشیم چی؟ مثلث کلا تغییر شکل میده بخاطر همین باید دو ضلع و زاویه بینشون داشته باشیم. داشتن دو ضلع و زاویه غیر بین، بینهایت مثلث مختلف به ما میده.
سلام
مطلب خیلی خوبی بود.
فقط یه نکته ای درباره همنهشتی ضلع دو زاویه و ضلع ودوزاویه بین بگم که خوب بود در متن هم گفته میشد اینه که در همنهشتی ضلع و دوزاویه حتما باید دقت بشه که اون دو ضلع مساوی متناظر هم اند. مثلا فرض کنید در مثلث abc و a’b’c’ , زاویه b برابر b’ و c برابر c’ و ضلع ab برابر a’c’ هست. با این که دو زاویه و ضلع برابر دارندولی نمیشه گفت همنهشتند .(چون این همنهشتی به همنهشتی دو زاویه و ضلع بین قابل تبدیل نیست.)
. یه نکته ی دیگه هم اینه که در اثبات قضایایی که باید قبل از اثبات قضیه مجموع زوایای داخلی مثلث میشه ۱۸۰ اثبات بشن مثل قضیه موازی مورب نمیشه ازاین همنهشتی استفاده کرد. واسه همین بهتره که کلا جزو همنهشتی ها محسوب نشه.
برای مثلث قائم الزاویه ، وتر و یک ضلع رو به عنوان حالت هم نهشتی بیان کردین در صورتی که در مثلث قائم الزاویه به دلیل رابطه ی فیثاغورس ، لزومی ندارد که حتماً وتر و یک ضلع هم نهشتی ایجاد کند ؛ بلکه حالت دو ضلع برای ایجاد هم نهشتی در مثلث قائم الزاویه کافی است و لزومی ندارد که حتماُ یک ضلع از آن دو ضلع ، وتر باشد
در کل در مثلث قائم الزاویه ، سه حالت مختص به این مثلث هم نهشتی ایجاد می کند :
دو ضلع
ضلع و زاویه ی حاده
ضلع و ارتفاع وارد بر وتر
و برای مثلث متساوی الساقین ، دو حالت مختص به این مثلث هم نهشتی ایجاد می کند :
ساق و قاعده
ضلع و زاویه
سلام و وقت بخیر؛
موارد ذکر شده به متن مقاله اضافه شدند.
از همراهیتان با مجله فرادرس سپاسگزاریم
سلام
من یک سوال از حالت همنهشتی دو ضلع و زاویه ی غیر بین داشتم.
من جایی ندیدم که این رو به عنوان حالت همنهشتی حساب کنن ولی سوالم اینه که خب اگه ما دو ضلع و زاویه ی غیر بین یه مثلث رو داشته باشیم میتونیم اون رو رسم کنیم.(برای این کار کافیه یک ضلعو رسم کنیم و با توجه به زاویه ای که داریم با نقاله از یک طرفش خط خارج میکنیم و بعد از طرف دیگه پاره خط به اندازه ضلع دیگه ای که داریم کمان میزنیم و محل برخورد خطی که خارج کردیم و کمان میشه راس سوم.)
خب وقتی که ما با دونستن دو ضلع و زاویه غیر بین(این رو هم بگم که میدونیم زاویه غیر بینمون مجاور با کدوم دو ضلعیه که اندازشونو داریم) میتونیم مثلث رو رسم کنیم واسه چی نمیتونیم بگیم که اگه دو ضلع و زاویه غیر بین مثلثی برابر باشن اون دوتا مثلث همنهشتند؟
من همیشه برای رسم مثلث قائم الزاویه با وض هم از همین روش استفاده میکردم ولی متوجه شدم که خب حتی اگه زاویه مون قائمه هم نباشه بازم این روش کار میکنه
لطفا جوابم رو بدین چون خیلی روش فکر کردم به نتیجه ای نرسیدم
در صفحه ی ۹۹ ریاضی هشتم ( محتوای تکمیلی استعداد درخشان ) مثال نقض هایی برای غیر هم نهشت بودن دو مثلث با دو ضلع و زاویه ی غیر بین برابر ارائه داده و در مورد اون صحبت کرده
سلام ممنون بسیار عالی و مفید بود، یک سوال داشتم، آیا دو مثلث با محیط و مساحت برابر، همنهشتند؟
نه لزوما
بسیار خوب سپاس فراوان
مفید بود ممنون
خیلی مفید بود
سپاس
عالی توضیح داده شده
باتشکر
عالییی ممنون از توضیحاتتون