معکوس تابع و تابع معکوس — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

پیش‌تر در بلاگ فرادرس دامنه و برد تابع،‌ تابع یک به یک و پوشا و دیگر مفاهیم مرتبط با تابع توضیح داده شدند. در این مطلب قصد داریم تا در مورد مفهومی تحت عنوان «معکوس تابع» (Inverse Function) صحبت کنیم.

مقدمه

همان‌گونه که در مطلب مفاهیم تابع نیز عنوان شد، یک تابع هم‌چون ماشین عمل می‌کند. در حقیقت تابع، ماشینی است که ورودی را گرفته و خروجی می‌دهد.

فیلم آموزش ریاضی 3 – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

برای نمونه در ادامه ماشینی ارائه شده که ورودیِ x را دریافت کرده، آن‌ را در ۲ ضرب و نهایتا عدد ۳ را به آن اضافه می‌کند.

معکوس تابع، عبارتی است که خروجی تابع را دریافت و به ما ورودی تابع را می‌دهد. برای نمونه معکوس تابع فوق،‌ به صورت زیر خواهد بود.

بنابراین می‌توان گفت معکوس تابع $$2 x + 3$$ برابر با $$\frac { y - 3 } { 2 }$$ است. معمولا معکوس یک تابع با علامت ۱- نشان داده می‌شود. البته توجه داشته باشید که این علامت به معنای توان نبوده و تنها یک نماد است. در حقیقت $$f ^ { - 1 } ( x )$$، معکوس تابع و $$f ( x ) ^ { - 1 }$$ نشان دهنده $$1 \over f(x)$$ است. بنابراین معکوس تابع به‌ صورت زیر نشان داده می‌شود.

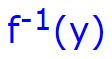
عبارت بالا «معکوس تابع f یا معکوس y» خوانده می‌شود. در نتیجه معکوس تابع $$f ( x ) = 2 x + 3$$ برابر با عبارت زیر است.

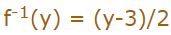
البته در تابع فوق می‌توان به جای y از هر متغیر دیگری نیز استفاده کرد. در اکثر موارد توابع معکوس را نیز بر حسب x بیان می‌کنند. برای نمونه به جای عبارت فوق می‌توان از $$f ^ {- 1 } ( x ) = \frac { x - 3} { 2 }$$ نیز استفاده کرد.

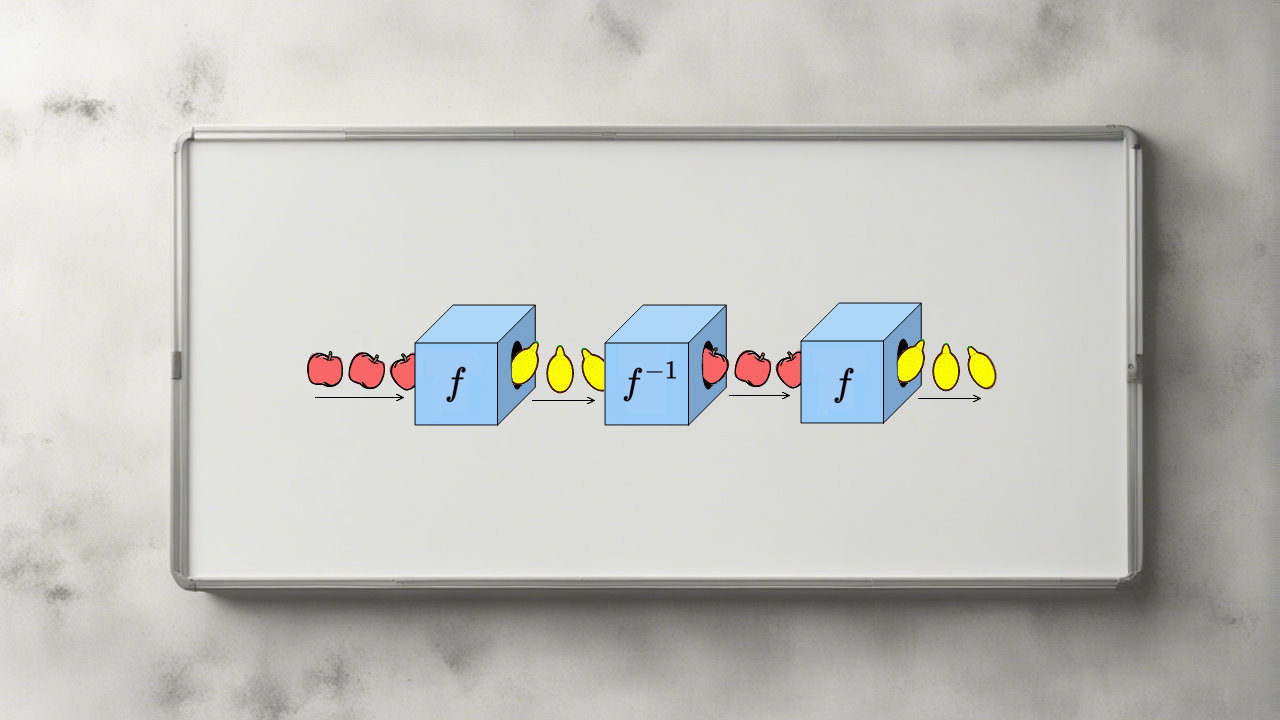
بازگشت به نقطه شروع

نکته جالب در مورد معکوس تابع این است که با استفاده از آن می‌توان به ورودی اولیه (یا همان x) دست یافت. بدین منظور کافی است به‌جای سیب و موز در طرح زیر، به‌ترتیب x و (f(x قرار داده شود!

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

مثال ۱

تابع $$2 x + 3$$ را در نظر بگیرید. با استفاده از این رابطه خواهیم داشت:

اگر عدد ۴ به عنوان ورودی در نظر گرفته شود، خروجی تابع برابر با ۱۱ است. در نتیجه اگر ۱۱ به عنوان ورودیِ معکوس تابع در نظر گرفته شود، خروجی آن نیز برابر با ۴ خواهد بود. به بیانی ریاضیاتی:

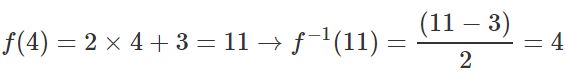
هم‌چنین می‌توان گفت:

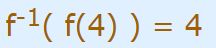
البته برای تابع f همواره رابطه‌ای به شکل زیر قابل بیان است.

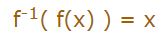
بیان فوق معادل با شکل ۱ است. البته رابطه فوق بصورت زیر نیز نوشته می‌شود.

بدست آوردن معکوس تابع

برای بدست آوردن معکوس یک تابع، در ابتدا به جای ضابطه‌ی (f(x تابع y قرار دهید، سپس معادله را به نحوی حل کنید که x بر حسب y بدست آید. سپس به‌ جای x عبارت $$f ^ {- 1 } ( x )$$ را قرار دهید. در نتیجه برای بدست آوردن معکوس یک تابع به ترتیب زیر عمل کنید.

1. در تابع به جای (f(x، عبارت y را قرار دهید.
2. معادله بدست آمده در قدم اول را بر حسب y حل کنید.
3. در رابطه بدست آمده در قدم دوم، به جای x، $$f ^{-1}( y )$$ قرار دهید.
4. $$f ^{-1}( y )$$ بدست آمده، معکوس تابع $$y = f ( x )$$ است.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

در ادامه مثالی ارائه شده که جهت درک بهتر موضوع می‌توانید به آن توجه کنید.

مثال ۲

معکوس تابع $$f ( x ) = 2 x + 3$$ را بیابید.

۱. در قدم اول به جای $$f ( x )$$، y قرار داده و به عبارت زیر می‌رسیم.

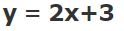
۲. عبارت بدست آمده در قدم اول بر حسب y حل شده و به رابطه زیر دست می‌یابیم.

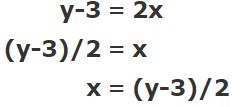
۳. حال اگر به جای x عبارت $$f ^ { - 1 } ( y )$$ قرار داده شود، تابع معکوس به صورت زیر بدست می‌آید.

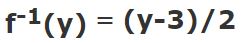
معکوس توابع معروف

در مثال‌های ارائه شده در فوق، تنها از چهار عمل اصلی استفاده شده که این امر حل آن‌ها را بسیار سهل کرده است. لذا در ادامه معکوس توابع معروف ذکر شده که در مواردی بایستی از آن‌ها نیز استفاده شود.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

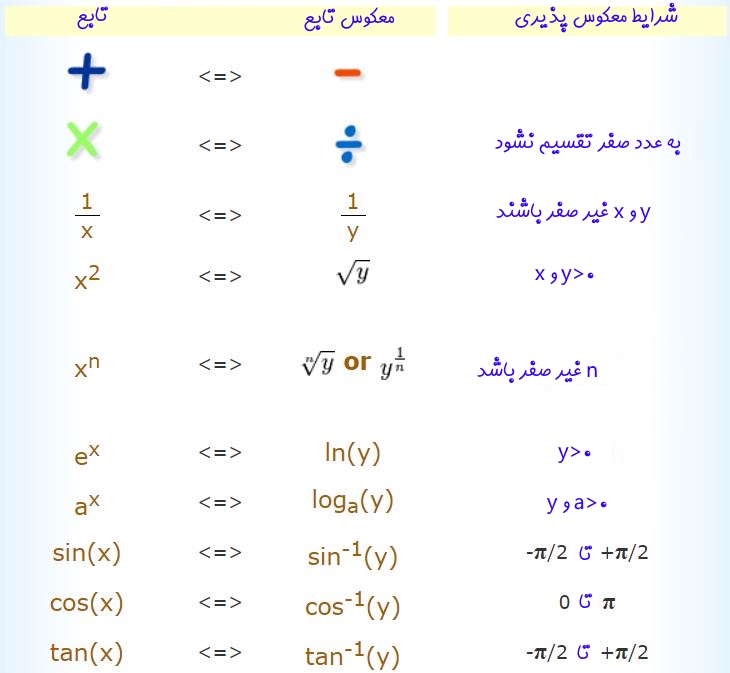
ستون سمت راست جدول فوق نیز بسیار مهم است. چرا که برخی توابع تنها می‌توانند در بازه‌ای خاص تعریف شوند. برای نمونه خروجی تابع سینوس ($$\sin x$$) بین ۱- تا ۱+ است؛ در نتیجه دامنه تابع معکوس سینوس ($$\sin^{-1} x$$) نیز می‌تواند تنها در این بازه باشد. در ادامه مثالی ارائه شده که اهمیتِ بررسی شرایط معکوس‌پذیری در آن نشان داده شده است.

مثال ۳

فرض کنید می‌خواهیم عدد ۲- را به توان ۲ رسانده و سپس مسیر عکس را طی کرده و از مقدار بدست آمده جذر بگیریم. با انجام این فرآیند داریم:

همان‌طور که می‌بینید با در نظر نگرفتن شرایط معکوس‌پذیری، استدلال درستی از تابع معکوس حاصل نشد. با توجه به جدول، معکوس تابع $$x ^ 2$$ زمانی وجود دارد که مقادیر x و y مثبت باشند (ردیف چهارم - ستون چهارم).

معکوس‌پذیری

شاید با مطالعه مثال ۳ این سئوال برایتان پیش آمده باشد که آیا هر تابعی می‌تواند معکوس داشته باشد؟ به‌منظور پاسخ به این سوال، بایستی با توابع یک به یک آشنایی داشته باشید.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

با توجه به تعریف تابع، به ازای یک ورودی نمی‌توان دو خروجی داشت. در تابع معکوس جای ورودی و خروجی با هم عوض شده‌اند. بنابراین تابعی که به ازای دو ورودی، یک خروجی یکسان داشته باشد، نمی‌تواند تابع معکوس داشته باشد. بنابراین تابعی می‌تواند معکوس داشته باشد که یک به یک باشد. برای نمونه در شکل زیر تابعی نشان داده شده که یک به یک است.

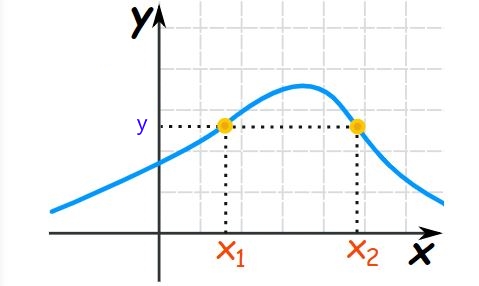
با معکوس کردن تابع فوق، به عبارتی می‌رسیم که در آن y ورودی و همزمان دو مقدار x₁ و x₂ خروجی هستند. در نتیجه نمی‌تواند معکوس داشته باشد. در شکل زیر نیز تابعی یک به یک ارائه شده، بنابراین معکوسی نیز برای آن وجود خواهد داشت.

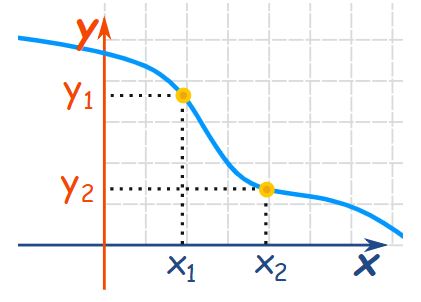
در مطلب تابع پوشا و یک به یک روش‌هایی ارائه شده که با استفاده از آن‌ها می‌توانید تابع بودن و یک به یک بودن یک نمودار را بدانید.

محدود کردن دامنه

در بالا عنوان شد که تابع یک به یک می‌تواند معکوس داشته باشد. اما واقعیت این است که می‌توان با محدود کردن دامنه یک تابع در بازه‌ای که یک به یک است، برای آن معکوس نوشت. برای نمونه تابعی را در بگیرید که نمودار آن مطابق با شکل زیر است.

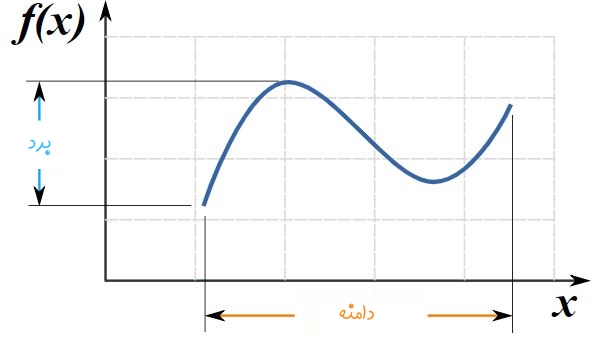
همان‌طور که می‌بینید تابع فوق یک به یک نیست. اما مطابق با نمودار شکل زیر، بازه‌ای را در نظر می‌گیریم که در آن دامنه تابع محدود شده است.

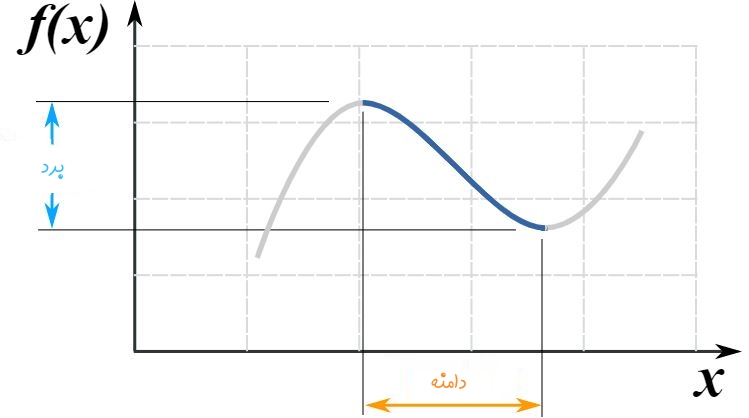
نمودار فوق در بازه نشان داده شده، دارای معکوس است؛‌ چرا که در این بازه، تابع یک به یک است. به‌منظور رسم کردن تابع معکوس، می‌توان نمودار تابع را نسبت به محور $$y = x$$ قرینه کرد. در نتیجه نمودار معکوسِ شکل فوق به‌صورت زیر است.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

بنابراین می‌توان گفت که همواره نمودار دو تابع (f(x و (f^-1(x نسبت به یکدیگر قرینه هستند.

مثال ۴

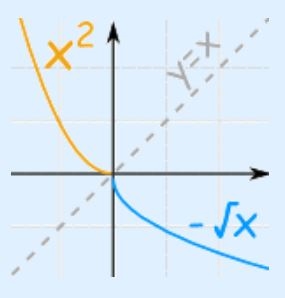
در بالا معکوس تابع $$x ^ 2$$ را به صورت $$\sqrt{x}$$ بدست آوردیم. توجه داشته باشید که تابع $$x ^ 2$$ در محدوده x‌>۰ بایستی تعریف شود. در این صورت تابع و معکوس آن به‌ صورت زیر خواهند بود.

حال تابع $$x ^ 2$$ را در بازه x<0 در نظر بگیرید. در این صورت معکوس آن به صورت $$f ( x ) = - \sqrt {x}$$ خواهد بود. هم‌چنین نمودار تابع و معکوسش به شکل زیر هستند.

مثال ۵

معکوس تابع $$g(x)={\frac { x - 3 } { x - 2 }: \enspace x > 3 }$$ را بیابید.

همان‌طور که در صورت سوال نیز نشان داده شده، تابع فوق به ازای مقادیر xهای بیشتر از ۳ در نظر گرفته شده؛ در این بازه مقدار تابع مثبت بوده و یک به یک است. در بالا نیز عنوان شد که در ابتدا به جای (f(x (یا همان (g(x در این مثال)، y را جایگذاری کرده و عبارت بدست آمده را بر حسب y بیابید. سپس به‌جای y از (g^-1(y استفاده شود. در ادامه این مراحل به‌ ترتیب انجام شده است.

بدیهی است که انتخاب متغیر به‌منظور بیان کردن یک تابع، امری اختیاری است. لذا می‌توان به جای y،‌ در رابطه فوق از x استفاده کرده و تابع معکوس را به‌صورت زیر بیان کرد.

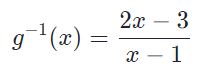
خلاصه

• معکوس تابع $$f ( x )$$ به صورت $$f ^ { - 1 } ( x )$$ نشان داده می‌شود.
• تابعی معکوس‌پذیر است که یک به یک باشد.
• می‌توان با محدود کردن دامنه تابعی غیر یک به یک، معکوس آن را نوشت.
• نمودار دو تابع $$f ( x )$$ و $$f ^ { - 1 } ( x )$$ نسبت به محور y=x قرینه هستند.