معادله صفحه — به زبان ساده

پیش‌تر در بلاگ فرادرس مفاهیم مربوط به معادله خط را مورد بررسی قرار دادیم. در این مطلب قصد داریم تا به اندازه یک بُعد فراتر رفته و معادله صفحه را در فضای سه‌بعدی توضیح دهیم.

معادله صفحه در فضا

فرض کنید می‌خواهیم معادله‌ی صفحه‌ای را بنویسیم که مختصات نقطه‌ای هم‌چون $$P _ 0 = (x _ 0 , y _ 0 , z _ 0)$$ روی آن معلوم است. همان‌طور که احتمالا می‌دانید به ‌منظور نوشتن معادله یک خط در فضای دوبعدی نیازمند شیب آن خط بودیم. در حالتی که با صفحه‌ای سه‌بعدی سر و کار داریم، آن‌چه که این نقش را ایفا می‌کند، بردار عمود به صفحه است. بنابراین به منظور نوشتن معادله یک صفحه بایستی یک نقطه از آن و بردار عمود به صفحه معلوم باشند. 

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

شکل زیر صفحه‌ای را نشان می‌دهد که در آن نقطه $$P _ 0$$ و بردار عمود $$\overrightarrow { n } < a , b , c >$$ مشخص شده است. در ابتدا نقطه‌ای فرضی همچون $$P = ( x , y , z )$$ را تصور کنید که روی صفحه قرار گرفته است.

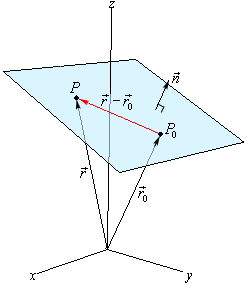
اگر از مبدا به نقاط P و P0 خطوطی رسم شوند، دو بردار بدست می‌آید. همان‌طور که در تصویر فوق نیز می‌بینید بردار $$\overrightarrow { r } - \overrightarrow { r_0 }$$ عمود بر بردار $$\overrightarrow { n }$$ عمود است. بنابراین حاصل‌ضرب داخلی بردار‌های $$\overrightarrow { r } - \overrightarrow { r_0 }$$ در $$\overrightarrow { n }$$ برابر با صفر است. در نتیجه می‌توان گفت:

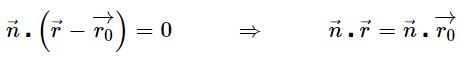
رابطه فوق در حقیقت معادله برداری یک صفحه خوانده می‌شود. بدیهی است که ما به دنبال شکل جبری معادله صفحه هستیم. شکلی مفید‌تر از رابطه فوق، به صورت زیر است. اگر بردار‌های r و r₀ به ترتیب به صورت $$< x , y , z >$$ و $$< x _ 0, y_ 0 , z_ 0 >$$ نوشته شوند، رابطه فوق به صورت زیر قابل بازنویسی خواهد بود:

$$\begin{align*}\left\langle { a , b , c } \right\rangle \small \bullet \left( {\left\langle { x , y, z} \right \rangle - \left\langle {{ x _0},{ y _0},{ z _0}} \right\rangle } \right)& = 0\\ \left\langle { a , b , c } \right\rangle \small \bullet \left\langle { x - { x _0}, y - {y_0}, z - {z_0}} \right\rangle & = 0\end{align*}$$

با انجام حاصل ضرب بالا، شکل کلی معادله صفحه به صورت زیر بدست می‌آید:

$$a \left ( { x - { x _ 0}} \right) + b \left( { y - { y _ 0}} \right) + c \left( { z - { z _ 0}} \right) = 0$$

رابطه فوق، شکل اسکالر معادله صفحه نامیده می‌شود. البته معادله بالا را به‌ صورت زیر نیز بیان می‌کنند:

$$a x + b y + c z = d$$

توجه داشته باشید که در رابطه بالا عدد d برابر با $$d = a { x _0} + b { y _0} + c { z _0}$$ است. بنابراین اگر رابطه‌ صفحه‌ای به صورت بالا بیان شود، بلافاصله می‌توان بردار عمود بر آن را به صورت زیر در نظر گرفت.

$$\overrightarrow n = \left \langle { a , b , c} \right \rangle$$

مثال ۱

معادله صفحه‌ای را بیابید که نقاط $$P = \left( {1, - 2,0} \right)$$ و $$Q = \left( { 3 , 1 , 4 } \right)$$ و $$R = \left( {0, - 1,2} \right)$$ روی آن قرار گرفته‌اند.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

نکته بسیار مهم در بدست آوردن معادله صفحه این است که در برخی از موارد ممکن است بردار عمود به صفحه به صورت مستقیم ارائه نشود. در این موارد دو بردار تشکیل داده و حاصل‌ضرب خارجی آن‌ها را برابر با بردار عمود وارد به صفحه در نظر بگیرید.

برای نمونه با توجه به دو نقطه ارائه شده دو بردار $$\overrightarrow { P Q }$$ و $$\overrightarrow { P R }$$ به ترتیب برابرند با:

$$\overrightarrow {P Q} = \left \langle {2,3,4} \right\rangle \hspace{ 0.25in }\hspace{0.25 in}\overrightarrow {P R} = \left\langle { - 1,1,2} \right\rangle$$

حال با استفاده از ضرب خارجی دو بردار داریم:

$$\overrightarrow n = \overrightarrow {PQ} \times \overrightarrow {PR} = \left| {\begin{array}{*{20}{c}}{\overrightarrow i}&{\overrightarrow j}&{\overrightarrow k}\\2&3&4\\{ - 1}&1&2\end{array}} \right|\,\,\,\, = 2\overrightarrow i - 8\overrightarrow j + 5\overrightarrow k$$

در نتیجه معادله صفحه به صورت زیر بدست می‌آید.

$$\begin{align*}2\left( { x - 1 } \right) - 8 \left( { y + 2} \right) + 5 \left( { z - 0} \right) & = 0\\ 2 x - 8 y + 5 z & = 18\end{align*}$$

مثال ۲

فرض کنید صفحه‌ای مطابق با رابطه $$- x + 2 z = 1 0$$ توصیف شود. وضعیت این صفحه نسبت به خط $$\overrightarrow r = \left\langle {5,2 - t,10 + 4 t} \right\rangle$$ به چه صورت است؟

در حقیقت هدف ما این است که بدانیم خط مفروض نسبت به صفحه ارائه شده عمود یا موازی است و یا این که صفحه را قطع می‌کند. با توجه به رابطه ارائه شده، بردار عمود به صفحه برابر با $$\overrightarrow n = \left\langle { - 1 , 0 , 2} \right \rangle$$ است. از طرفی با توجه به رابطه ارائه شده برای $$\overrightarrow {r}$$، بردار موازی این خط به صورت $$v = \left \langle {0, - 1,4} \right \rangle$$ است.

همان‌طور که می‌دانید اگر حاصل ضرب خارجی دو بردار برابر با صفر باشد، به معنی آن است که دو بردار مفروض موازی هم هستند. بنابراین اگر حاصل ضرب خارجی دو بردار v و n نیز برابر با صفر باشد، دو بردار موازی بوده و خط r عمود بر صفحه است. در نتیجه حاصل ضرب خارجی دو بردار برابر است با:

$$\overrightarrow n \times \overrightarrow v = \left| {\begin{array}{*{20}{c}}{\overrightarrow i}&{\overrightarrow j}&{\overrightarrow k}\\{ - 1}&0&2\\0&{ - 1}&4\end{array}} \right|\,\,\,\, = 2\overrightarrow i + 4\overrightarrow j + \overrightarrow k \ne \overrightarrow 0$$

بنابراین خط r قطعا عمود به صفحه نیست. در حقیقت ممکن است خط r موازی با صفحه باشد. به منظور اعتبارسنجی این موضوع نیز می‌توان از ضرب داخلی استفاده کرد. همان‌طور که می‌دانید اگر حاصل ضرب داخلی دو بردار برابر با صفر باشد، در این صورت دو بردار عمود به یکدیگر بوده و خط r موازی صفحه خواهد بود. در نتیجه حاصل ضرب داخلی دو بردار برابر است با:

$$\overrightarrow n\small \bullet \overrightarrow v = 0 + 0 + 8 = 8 \ne 0$$

حاصل ضرب داخلی غیر صفر بوده که به معنای آن است دو بردار عمود به یکدیگر نیستند. لذا خطِ r نه موازی صفحه و نه عمود بر آن است.

مثال ۳

معادله گذرنده از سه نقطه (1,2,3)، (۲,4,6) و (9-,6-,3-) را بیابید. همان‌طور که قبلا نیز بیان شد، معمولا در حالاتی که نقاطی روی صفحه به منظور نوشتن معادله ارائه می‌شود، بهتر است در ابتدا دو بردار تشکیل داده و با استفاده از ضرب خارجی آن‌ها، بردار عمود به صفحه را بدست آورد.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

در شکل زیر می‌بینید که با استفاده از ۳ نقطه دو بردار تشکیل شده و با توجه به قرار داشتن آن‌ها در یک صفحه حاصل‌ضرب خارجیشان به صفحه عمود شده است.

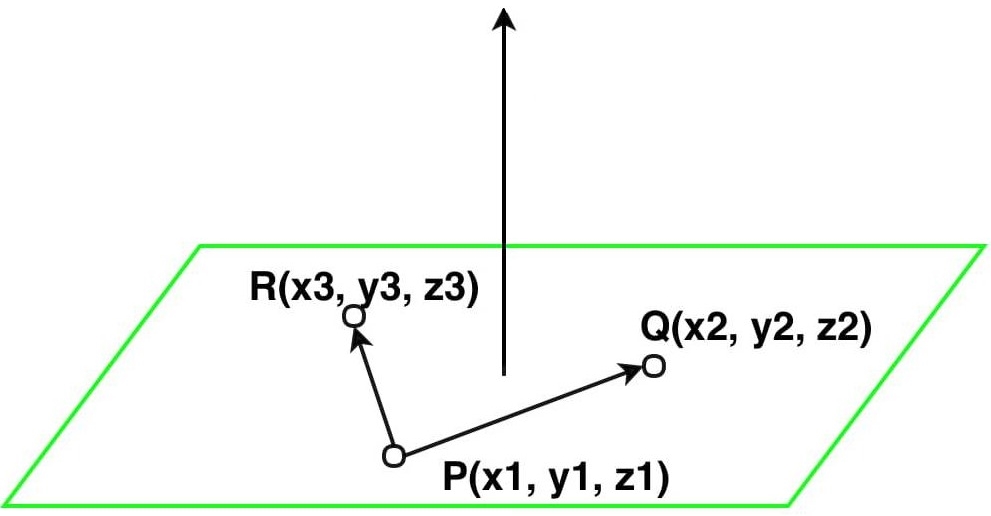
در این حالت نیز در ابتدا دو بردار b و c را به صورت زیر بدست می‌آوریم.

$$\overrightarrow{b} = (2,4,6) - (1,2,3) = (1,2,3) \enspace , \enspace \overrightarrow{c} =(1,2,3) - (-3,-6,-9) = (4, 8, 12)$$

در مرحله بعد حاصل ضرب خارجی دو بردار فوق به صورت زیر بدست می‌آید.

$$\begin{align*} \overrightarrow{n} &= \overrightarrow{b} \times \overrightarrow{c}\\ &= \left| \begin{array}{rrr} \overrightarrow{ i } & \overrightarrow{ j } & \overrightarrow{ k }\\ 1 & 2 & 3\\ 4 & 8 & 12 \end{array} \right| \\ &= \overrightarrow { i } (24 -24) - \overrightarrow { j } (12 -12) + \overrightarrow { k } (8 -8)\\ &= (0, 0, 0) \end{align*}$$

همان‌طور که می‌بینید حاصل ضرب خارجی این دو بردار برابر با صفر است! حال این سوال مطرح می‌شود که صفر بودن ضرب خارجی به چه معنا و معادله صفحه به چه صورت قابل دست یابی است؟

توجه داشته باشید که ما با سه نقطه مواجه هستیم که حاصل ضرب خارجی بردار‌های ایجاد شده‌ در نتیجه آن‌ها، برابر با صفر است. این جمله به معنای آن است که سه نقطه روی یک خط قرار دارند. لذا سه نقطه‌ی روی یک خط، شرایطی کافی به‌منظور توصیف یک صفحه را دارا نیستند. برای نمونه همان‌طور که در شکل زیر نیز مشاهده می‌کنید، سه نقطه وجود دارد که دو صفحه‌ی متفاوت می‌تواند خط گذرنده از آن‌ها را قطع کند.

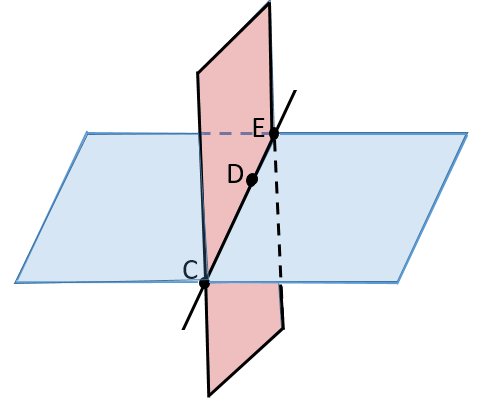
مثال ۴

معادله دو صفحه به صورت $$3x + 6y - 5z = - 3$$ و $$- 2x + 7y - z = 24$$ است. با فرض این که دو صفحه در یک خط همدیگر را قطع کنند، معادله خط مذکور را بیابید.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

احتمالا همان‌طور که می‌دانید برای نوشتن معادله یک خط نیازمند بردار هادی و یک نقطه از آن هستیم. بدیهی است که نقطه قرار گرفته روی خط متقاطع، روی هر دو صفحه نیز قرار خواهد داشت. هم‌چنین واضح است که خط مقطع دو صفحه یکی از صفحات اصلی را قطع می‌کند. برای نمونه در ابتدا z=0 را در معادله دو صفحه قرار می‌دهیم. در این صورت با حل دو معادله بدست آمده، محل تقاطع خط مشترک با صفحه‌ی z بدست می‌آید.

$$\begin {align*} 3 x + 6 y & = - 3\\ - 2 x + 7 y & = 24 \end {align*}$$

با حل دستگاه دو معادله دو مجهول فوق، مقادیر x و y برابرند با:

$$x = - 5\hspace{0.5in}\,\,\,\,y = 2$$

مقادیر بدست آمده x و y نشان می‌دهند که خط مشترک دو صفحه مذکور، صفحه‌ی x-y را در نقطه $$\left( { - 5 , 2 , 0 } \right)$$ قطع می‌کند. از طرفی هما‌نطور که در شکل زیر نشان داده شده بردار هادی خط مشترک دو صفحه، به بردار‌های نرمال دو صفحه عمود هستند.

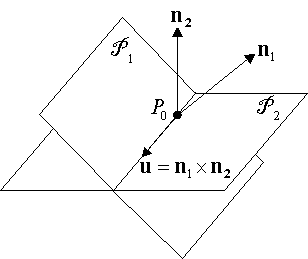
لذا بردار هادی را می‌توان برابر با حاصل‌ضرب خارجی بردار‌های نرمال تصور کرد. با توجه به رابطه دو صفحه، بردار‌های نرمال آن‌ها برابرند با:

$${ \overrightarrow n_1} = \left \langle {3,6, - 5} \right \rangle \hspace { 0.75 in } { \overrightarrow n_2} = \left\langle { - 2 , 7, - 1} \right \rangle$$

در نتیجه حاصل ضرب خارجی دو بردار برابر است با:

$$ \begin{align*}{ { \overrightarrow n}_1} \times {{\overrightarrow n}_2} = \left| {\begin{array}{*{20}{c}}{\overrightarrow i}&{\overrightarrow j}&{\overrightarrow k}\\3&6&{ - 5}\\{ - 2}&7&{ - 1}\end{array}} \right| = - 6\overrightarrow i + 10\overrightarrow j + 21\overrightarrow k - \left( { - 3\overrightarrow j} \right) - \left( { - 35 \overrightarrow i} \right) - \left( { - 12\overrightarrow k} \right) = 29 \overrightarrow i + 13 \overrightarrow j + 33\overrightarrow k\end {align*} $$

در مرحله آخر، شکل پارامتری معادله خط در فضا نیز به صورت زیر بدست می‌آید.

$$ \require{bbox} \bbox[2pt,border:1px solid black]{{\overrightarrow r\left( t \right) = \left\langle { - 5,2,0} \right\rangle + t\left\langle {29,13,33} \right\rangle = \left\langle { - 5 + 29t,2 + 13t,33t} \right\rangle }} $$