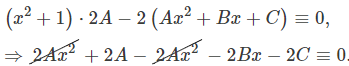در راستای معرفی مفاهیم مربوط به معادلات دیفرانسیل، در این مطلب قصد داریم تا نحوه حل معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر را توضیح دهیم. از این رو به منظور درک بهتر پیشنهاد میشود مطالب معادلات دیفرانسیل مرتبه دوم و معادلات دیفرانسیل را مطالعه فرمایید.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
مقدمه
توجه داشته باشید که هدف ما یافتن پاسخ معادله دیفرانسیل مرتبه دوم خطی است. از این رو در ابتدا باید با شکل کلی این نوع از معادلات آشنا باشید. شکل کلی یک معادله دیفرانسیل مرتبه دوم با ضرایب متغیر به صورت زیر است.
y ′ ′ + a 1 ( x ) y ′ + a 2 ( x ) y = 0 \large { y ^ { \prime \prime } + { a _ 1 } \left ( x \right ) y ^ { \prime } } + { { a _ 2 } \left ( x \right ) y } ={ 0 } y ′′ + a 1 ( x ) y ′ + a 2 ( x ) y = 0
این نکته را نیز در نظر بگیرید که ضرایب a 1 ( x ) a_1(x) a 1 ( x ) a 2 ( x ) a_2(x) a 2 ( x ) [ a , b ] \left [ { a , b } \right ] [ a , b ]
رونسکین
توابع y 1 ( x ) , y 2 ( x ) , … , y n ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right ) , \ldots , { y _ n } \left ( x \right ) y 1 ( x ) , y 2 ( x ) , … , y n ( x ) α 1 , α 2 , … , α n { \alpha _ 1 } , { \alpha _ 2 } , \ldots , { \alpha _ n } α 1 , α 2 , … , α n
α 1 y 1 ( x ) + α 2 y 2 ( x ) + … + α n y n ( x ) ≡ 0 \large { { \alpha _ 1 } { y _ 1 } \left ( x \right ) + { \alpha _ 2 } { y _ 2 } \left ( x \right ) + \ldots } + { { \alpha _ n } { y_ n } \left ( x \right ) } \equiv { 0 } α 1 y 1 ( x ) + α 2 y 2 ( x ) + … + α n y n ( x ) ≡ 0
اگر رابطه فوق تنها در زمانی درست باشد که تمامی ضرایب α \alpha α α 1 = α 2 = … { \alpha _1 } = { \alpha _ 2 } = \ldots α 1 = α 2 = … y y y y 1 ( x ) y_1(x) y 1 ( x ) y 2 ( x ) y_2(x) y 2 ( x )
y 1 ( x ) y 2 ( x ) ≠ const \large \frac { { { y _1 } \left ( x \right ) } }{ { { y _ 2 } \left ( x \right ) } } \ne \text {const } y 2 ( x ) y 1 ( x ) = const
در غیر این صورت دو تابع نسبت هم وابسته خطیاند. حال به منظور بررسی وابستگی n n n y 1 ( x ) , y 2 ( x ) , … , y n ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right), \ldots , { y _ n } \left ( x \right ) y 1 ( x ) , y 2 ( x ) , … , y n ( x ) n − 1 n-1 n − 1 n − 1 n-1 n − 1
$$ \large {W\left( x \right) = {W_{{y_1},{y_2}, \ldots ,{ y _ n } } } \left ( x \right ) }<br />
= {\left| {\begin{array}{*{20} { c } } { { y _ 1 } } & { { y _ 2 } } & \ldots &{{y_n}}\\<br />
{{y ^{\prime} _ 1 } } & { { y ^ { \prime } _ 2 } } & \ldots & { { y ^ { \prime } _ n } } \\<br />
\ldots & \ldots & \ldots & \ldots \\ { y _ 1 ^ { \left( {n – 1} \right ) } } & { y _ 2 ^ { \left ( { n – 1 } \right)}}& \ldots &{y_n^{\left( {n – 1 } \right ) } } \end{array}} \right|}$$
آزمون رونسکین
اگر سیستم توابع y 1 ( x ) , y 2 ( x ) , … , y n ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right), \ldots , { y _ n } \left ( x \right ) y 1 ( x ) , y 2 ( x ) , … , y n ( x ) [ a , b ] [a,b] [ a , b ] y 1 ( x ) , y 2 ( x ) , … , y n ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right), \ldots , { y _ n } \left ( x \right ) y 1 ( x ) , y 2 ( x ) , … , y n ( x )
سیستم پاسخهای پایه
دو پاسخ خصوصی مستقلِ یک معادله دیفرانسیل همگن مرتبه دوم، تشکیلدهنده سیستم پاسخهای پایه معادله مذکور هستند.
در حقیقت اگر y 1 ( x ) , y 2 ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right ) y 1 ( x ) , y 2 ( x )
y ( x ) = C 1 y 1 ( x ) + C 2 y 2 ( x ) \large { y \left ( x \right) } = { { C _ 1 } { y _ 1 } \left ( x \right ) + { C _ 2} { y _2 } \left ( x \right ) } y ( x ) = C 1 y 1 ( x ) + C 2 y 2 ( x )
در رابطه فوق C C C y 1 ( x ) , y 2 ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right ) y 1 ( x ) , y 2 ( x )
$$\large \left| {\begin{array}{*{20} { c } } { { y _ 1} } & { { y_2}} & y \\ { { y ^ { \prime } _ 1 } } & { { y ^ {\prime} _ 2 } } & y ^ { \prime } \\ { { y ^ { \prime \prime} _ 1} } & { { y^ { \prime \prime } _ 2 } } & y ^ { \prime \prime } \end{array} } \right| = 0 $$
فرمول لیوویل
بنابراین همانطور که در بالا نیز اشاره شد، پاسخ عمومی یک معادله دیفرانسیل همگن، ترکیبی خطی از دو پاسخ خصوصیِ مستقلِ y 1 ( x ) , y 2 ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right ) y 1 ( x ) , y 2 ( x ) W ( x ) W(x) W ( x ) y 1 ( x ) y_1(x) y 1 ( x ) y 2 ( x ) y_2(x) y 2 ( x ) a 1 ( x ) a_1(x) a 1 ( x )
به منظور بدست آوردن این فرمول در ابتدا W ( x ) W(x) W ( x ) y 1 ( x ) , y 2 ( x ) { y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right ) y 1 ( x ) , y 2 ( x )
y ′ ′ + a 1 ( x ) y ′ + a 2 ( x ) y = 0 \large { y ^ { \prime \prime } + { a _ 1 } \left ( x \right ) y ^ { \prime } } + { { a _ 2 } \left ( x \right ) y } = { 0 } y ′′ + a 1 ( x ) y ′ + a 2 ( x ) y = 0
توجه داشته باشید که دو ضریب a 1 ( x ) a_1(x) a 1 ( x ) a 2 ( x ) a_2(x) a 2 ( x ) [ a , b ] [a,b] [ a , b ] x 0 x_0 x 0 x ∈ [ a , b ] x \in \left [ { a , b } \right ] x ∈ [ a , b ]
W ( x ) = W ( x 0 ) exp ( – ∫ x 0 x a 1 ( t ) d t ) \large { W \left( x \right ) } = { W \left ( { { x _ 0 } } \right ) \exp \left ( { – \int\limits _ { { x _0 } } ^ x { { a _1 } \left ( t \right ) d t } } \right ) } W ( x ) = W ( x 0 ) exp – x 0 ∫ x a 1 ( t ) d t
حل معادله دیفرانسیل همگن مرتبه دو
متاسفانه روشی کلی به منظور یافتن پاسخ خصوصی یک معادله وجود ندارد. معمولا پاسخ خصوصی با استفاده از شکل و ضرایب معادله، حدس زده میشود. اگر پاسخ خصوصی y 1 ( x ) ≠ 0 { y _ 1 } \left ( x \right ) \ne 0 y 1 ( x ) = 0 y = y 1 ( x ) z ( x ) y = { y _ 1 } \left ( x \right ) z \left ( x \right ) y = y 1 ( x ) z ( x ) z ′ ( x ) = u z ^ { \prime } \left ( x \right ) = u z ′ ( x ) = u
روش دیگر کاهش مرتبه معادله دیفرانسیل، مبتنی بر فرمول لیوویل است. در این روش پاسخ خصوصی y 1 ( x ) y_1(x) y 1 ( x )
مثال ۱
وضعیت وابستگی دو تابع y 1 ( x ) = x + 2 { y _1 } \left ( x \right ) = x + 2 y 1 ( x ) = x + 2 y 2 ( x ) = 2 x – 1 { y _ 2 } \left ( x \right ) = 2 x – 1 y 2 ( x ) = 2 x –1
همانطور که در بالا نیز بیان شد، سریعترین روش به منظور بررسی وابستگی دو تابع، محاسبه تقسیم آنها است. بنابراین این حاصل تقسیم برابر است با:
y 1 ( x ) y 2 ( x ) = x + 2 2 x – 1 = x – 1 2 + 5 2 2 x – 1 = 1 2 ( 2 x – 1 ) + 5 2 2 x – 1 = 1 2 + 5 2 ( 2 x – 1 ) = 1 2 + 5 4 x – 2 \large \begin {align*} \frac { { { y _ 1 } \left( x \right)}}{{{y_2}\left( x \right)}} & = {\frac{{x + 2 } } { {2 x – 1}} } \\ & = {\frac { { x – \frac { 1 } { 2 } + \frac{5}{2}}}{{2x – 1}} } = {\frac { { \frac{ 1 } { 2 } \left( {2x – 1} \right ) + \frac { 5 } {2 } } } { { 2 x – 1 } } } \\ & = { \frac { 1 } { 2 } + \frac { 5 } { { 2 \left( {2x – 1} \right ) } } } = {\frac { 1 } { 2 } + \frac{5}{{4x – 2 } } } \end {align*} y 2 ( x ) y 1 ( x ) = 2 x –1 x + 2 = 2 x –1 x – 2 1 + 2 5 = 2 x –1 2 1 ( 2 x –1 ) + 2 5 = 2 1 + 2 ( 2 x –1 ) 5 = 2 1 + 4 x –2 5
همانطور که میبینید حاصل تقسیم برابر با عددی ثابت نیست؛ بنابراین این دو تابع مستقل خطیاند.
مثال ۲
رونسکین دو تابع y 1 ( x ) = cos x { y _1 } \left ( x \right ) = \cos x y 1 ( x ) = cos x y 2 ( x ) = sin x { y _ 2 } \left ( x \right ) = \sin x y 2 ( x ) = sin x
رونسکین دو تابع برابر با دترمینان زیر است.
$$ { { W _{ { y _ 1 } , { y _ 2 } } } \left( x \right) } = { \left| { \begin {array}{*{20}{c}}<br />
{ { y _ 1 } \left( x \right ) } & { { y _ 2 } \left ( x \right ) } \\ { { y ^ { \prime } _ 1 } \left( x \right ) } & { { y ^ { \prime } _ 2 } \left ( x \right ) }<br />
\end {array}} \right| } $$
در نتیجه با قرار دادن دو تابع سینوس و کسینوس در رابطه فوق، اندازه رونسکین برابر است با:
$$ \large { { W_ { { y _ 1 } , { y _ 2 } } } \left ( x \right ) } = { \left| { \begin {array} {*{ 20 } { c } } { \cos x } & { \sin x } \\ { – \sin x } & { \cos x }<br />
\end {array} } \right| } = { { \cos ^ 2 } x + { \sin ^ 2 } x = 1 } $$
با توجه به غیر صفر بودن رونسکین، میتوان نتیجه گرفت که این دو تابع مستقل خطیاند.
مثال ۳
معادله دیفرانسیلی را بدست آورید که پاسخهای پایهای آن دو تابع x x x e x e^x e x
در ابتدا باید مشتقات دو تابع را به صورت زیر بدست آوریم.
y 1 ′ = x ′ = 1 , y 1 ′ ′ = 1 ′ = 0 \large { { y ^ { \prime } _ 1 } = x ^ { \prime } = 1 \ \ , \;\;}\kern-0.3pt { {y ^ { \prime \prime } _1 } = 1 ^ { \prime } = 0 } y 1 ′ = x ′ = 1 , y 1 ′′ = 1 ′ = 0
y 2 ′ = ( e x ) ′ = e x , y 2 ′ ′ = ( e x ) ′ = e x \large { { y ^ { \prime } _ 2 } = { \left ( { { e ^ x } } \right ) ^ \prime } = { e ^ x } \ \ ,\;\;}\kern 0.3pt { { y ^ { \prime \prime } _ 2 } = { \left ( { { e ^ x } } \right ) ^ \prime } = { e ^ x } } y 2 ′ = ( e x ) ′ = e x , y 2 ′′ = ( e x ) ′ = e x
معادله دیفرانسیل مربوطه باید شرایط زیر را ارضا کند.
$$ \large {\left| {\begin{array}{*{20}{c}} { { y _ 1 } } & { { y _2 } } & y \\ { { y ^ { \prime } _ 1 } } & { { y ^ { \prime } _ 2 } } & y ^ { \prime } \\ { { y ^ { \prime \prime } _ 1} } & { { y ^ { \prime \prime } _ 2 } } & y ^ { \prime \prime } \end {array} } \right| = 0 \; \; } \Rightarrow { \left| { \begin {array}{*{20 } { c } } x & { { e ^ x } }&y\\ 1& { { e ^ x } } & y ^ { \prime } \\ 0 & { { e^ x } } & y ^ { \prime \prime } \end {array} } \right| = 0 }$$
اگر دترمینان را مبتنی بر ستون اول ماتریس بسط دهیم، خواهیم داشت:
x ( e x y ′ ′ – e x y ′ ) − 1 ⋅ ( e x y ′ ′ – e x y ) = 0 ⇒ e x [ ( x y ′ ′ – x y ′ ) − ( y ′ ′ – y ) ] = 0 \large \begin {align*} {{x\left( { { e ^ x }y ^ { \prime \prime } – { e ^ x } y ^ { \prime } } \right) }-{ 1 \cdot \left ( { { e ^ x } y ^ { \prime \prime } – { e ^ x } y } \right ) = 0}} \\ \Rightarrow { { { e ^ x }\left[ {\left( { x y ^ { \prime \prime} – xy ^ {\prime} } \right) }\right.}-{\left.{ \left( { y ^ { \prime \prime } – y } \right ) } \right] = 0 } } \end {align*} x ( e x y ′′ – e x y ′ ) − 1 ⋅ ( e x y ′′ – e x y ) = 0 ⇒ e x [ ( x y ′′ – x y ′ ) − ( y ′′ – y ) ] = 0
با توجه به غیر صفر بودنِ عبارتِ نمایی (e x ≠ 0 , {e^x} \ne 0, e x = 0 ,
x y ′ ′ – x y ′ – y ′ ′ + y = 0 ⇒ ( x – 1 ) y ′ ′ – x y ′ + y = 0 \large { x y ^ { \prime \prime } – x y ^ { \prime } – y ^ { \prime \prime} + y = 0 \;\;} \Rightarrow { \left ( { x – 1} \right ) y ^ { \prime \prime } – x y ^ { \prime } + y = 0 } x y ′′ – x y ′ – y ′′ + y = 0 ⇒ ( x –1 ) y ′′ – x y ′ + y = 0
مثال ۴
پاسخ عمومی معادله x 2 y ′ ′ – 2 x y ′ + 2 y = 0 { x ^ 2 } y ^ { \prime \prime } – 2 x y ^ { \prime } + 2 y = 0 x 2 y ′′ –2 x y ′ + 2 y = 0 y 1 = x y_1=x y 1 = x
همانطور که بیان شد در این حالت از تغییر متغیر y = y 1 z = x z y = { y _ 1 } z = x z y = y 1 z = x z y y y
y ′ = ( x z ) ′ = z + x z ′ , y ′ ′ = ( z + x z ′ ) ′ = z ′ + z ′ + x z ′ ′ = 2 z ′ + x z ′ ′ \large \begin {align*} y ^ { \prime } & = { \left ( { x z } \right ) ^ \prime } \\ & = z + x z ^ { \prime } ,\kern-0.3pt { y ^ { \prime \prime} = { \left ( { z + x z ^ { \prime } } \right ) ^ \prime } } \\ & = {z ^ { \prime } + z ^ { \prime } + x z ^ { \prime\prime} } \\ & = { 2 z ^{\prime} + x z ^ { \prime \prime } } \end {align*} y ′ = ( x z ) ′ = z + x z ′ , y ′′ = ( z + x z ′ ) ′ = z ′ + z ′ + x z ′′ = 2 z ′ + x z ′′
پس از قرار دادن مشتق محاسبه شده در معادله، به رابطه زیر میرسیم.
با جایگذاری z ′ = p z ^ { \prime } = p z ′ = p x 3 p ′ = 0 { x ^ 3 } p ^ { \prime } = 0 x 3 p ′ = 0
p = C 1 \large p = { C _ 1 } p = C 1
در نتیجه تابع z z z
p = C 1 ⇒ z ′ = C 1 ⇒ z = C 1 x + C 2 \large { p = { C _ 1 } \; \; } \Rightarrow { z ^ { \prime } = { C _ 1 } \; \; } \Rightarrow { z = { C _ 1 } x + { C _2 } } p = C 1 ⇒ z ′ = C 1 ⇒ z = C 1 x + C 2
با بدست آمدن z z z y y y
y ( x ) = x z = x ( C 1 x + C 2 ) = C 1 x 2 + C 2 x \large { y \left ( x \right ) = x z } = { x \left ( { { C _1 } x + { C _ 2 } } \right ) } = { { C _ 1 } { x ^ 2 } + { C _ 2 } x } y ( x ) = x z = x ( C 1 x + C 2 ) = C 1 x 2 + C 2 x
مثال ۵
پاسخ عمومی معادله زیر را بیابید.
( x 2 + 1 ) y ′ ′ – 2 y = 0 \large \left ( { { x ^ 2 } + 1 } \right ) y ^ { \prime \prime } – 2 y = 0 ( x 2 + 1 ) y ′′ –2 y = 0
در ابتدا با توجه به شکل تابع، تابعی از درجه ۲ را به عنوان حدس اولیه در نظر میگیریم. این تابع به صورت زیر است.
y 1 = A x 2 + B x + C \large { y _ 1 } = A { x ^ 2 } + B x + C y 1 = A x 2 + B x + C
در نتیجه مشتقات اول و دوم تابع نیز به صورت زیر بدست خواهند آمد.
y 1 ′ = 2 A x + B , y 1 ′ ′ = 2 A \large { { y ^ { \prime } _1 } = 2 A x + B,\;\;}\kern-0.3pt { { y ^ { \prime \prime } _ 1 } = 2 A } y 1 ′ = 2 A x + B , y 1 ′′ = 2 A
با قرار دادن مشتقات بدست آمده در معادله اصلی، ضرایب ثابت A , B , C A,B,C A , B , C
بنابراین رابطه بین ضرایب ثابت به صورت زیر خواهد بود:
{ – 2 B = 0 2 A – 2 C = 0 ⇒ { B = 0 A = C \large { \left \{ \begin {array} { l } – 2 B = 0 \\ 2 A – 2 C = 0 \end {array} \right. \;\; } \Rightarrow { \left \{ \begin{array} { l } B = 0 \\ A = C \end {array} \right.} { –2 B = 0 2 A –2 C = 0 ⇒ { B = 0 A = C
در نتیجه شکل تابع به صورت y 1 = C ( x 2 + 1 ) y _1 = C \left ( { { x ^ 2 } + 1 } \right ) y 1 = C ( x 2 + 1 )
y 1 = x 2 + 1 \large { y _ 1 } = { { x ^ 2 } + 1 } y 1 = x 2 + 1
با توجه به بدست آمدن y 1 y_1 y 1
y = y 1 z = ( x 2 + 1 ) z ⇒ y ′ = 2 x z + ( x 2 + 1 ) z ′ ⇒ y ′ ′ = 2 z + 2 x z ′ + 2 x z ′ + ( x 2 + 1 ) z ′ ′ = 2 z + 4 x z ′ + ( x 2 + 1 ) z ′ ′ \begin {align*} y & = {y_1}z = \left( {{x^2} + 1} \right)z \\ & \Rightarrow y ^ { \prime } = 2xz + \left( { { x ^ 2 } + 1 } \right ) z ^ { \prime } \\ & \Rightarrow { { y ^ { \prime \prime } = 2 z + 2 x z ^{\prime} + 2 x z ^ { \prime } } + { \left( { { x ^ 2 } + 1} \right ) z ^ { \prime \prime } } } = { { 2 z + 4 x z ^ {\prime} } + { \left ( { { x ^2 } + 1 } \right )z ^ { \prime \prime } } } \end {align*} y = y 1 z = ( x 2 + 1 ) z ⇒ y ′ = 2 x z + ( x 2 + 1 ) z ′ ⇒ y ′′ = 2 z + 2 x z ′ + 2 x z ′ + ( x 2 + 1 ) z ′′ = 2 z + 4 x z ′ + ( x 2 + 1 ) z ′′
در نتیجه با جایگذاری y y y
$$ \large \begin {align*} \require {cancel} { { \left( {{x^2} + 1} \right) \cdot}\kern0pt{ \left[ {2z + 4 x z ^{\prime} + \left( {{x^2} + 1} \right)z^{\prime\prime}} \right] }-{ 2\left( {{x^2} + 1} \right)z }={ 0}} \\ \Rightarrow {{\left( {{x^2} + 1} \right) \cdot}}\kern0pt{{ \left[ {\cancel { 2 z } + 4xz ^{\prime} + \left( { { x ^ 2 } + 1} \right ) z ^ { \prime \prime } – \cancel { 2 z } } \right] } = { 0 } } \\ \Rightarrow { \left( { { x ^ 2 } + 1} \right)z ^{ \prime \prime } + 4 x z ^ { \prime } = 0 } \end {align*} $$
در این مرحله نیاز است تا از تغییر متغیر دوم نیز استفاده شود. این تغییر متغیر به صورت z ′ = p ( x ) z ^ { \prime } = p \left ( x \right ) z ′ = p ( x )
( x 2 + 1 ) p ′ + 4 x p = 0 \large \left ( { { x ^ 2 } + 1 } \right ) p ^ { \prime } + 4 x p = 0 ( x 2 + 1 ) p ′ + 4 x p = 0
حال ما با معادلهای از مرتبه اول روبرو هستیم که میتوان آن را با استفاده از روش جداسازی متغیرها حل کرد. بنابراین حاصل انتگرال برابر است با:
( x 2 + 1 ) d p d x = – 4 x p ⇒ d p p = – 4 x d x x 2 + 1 ⇒ ∫ d p p = – 2 ∫ d ( x 2 + 1 ) x 2 + 1 ⇒ ln ∣ p ∣ = – 2 ln ( x 2 + 1 ) + ln C 1 ⇒ ln ∣ p ∣ = ln C 1 ( x 2 + 1 ) 2 ⇒ p = C 1 ( x 2 + 1 ) 2 \large \begin {align*} \left( { { x ^ 2 } + 1 } \right ) \frac { { d p} } {{ d x } } = – 4 x p \;\; & \Rightarrow { \frac { { d p } } { p } = – \frac{{4x dx } } {{ { x ^ 2 } + 1}} \;\;} \\ & \Rightarrow { { \int {\frac{{dp}}{p}} }={ – 2\int {\frac { { d \left( {{x^2} + 1} \right)}}{{{x^2} + 1 } } } \;\;}} \\ & \Rightarrow { { \ln \left| p \right| } = { – 2\ln \left( { { x ^ 2 } + 1} \right) }+{ \ln {C_1} \;\; } } \\ & \Rightarrow { \ln \left| p \right| = \ln \frac{ { { C _ 1} } } { { {{\left( { { x ^ 2 } + 1} \right ) }^ 2}}} \;\;} \\ & \Rightarrow {p = \frac { { {C _ 1 } } }{ {{ { \left ( { { x ^ 2 } + 1} \right ) } ^ 2}} } } \end {align*} ( x 2 + 1 ) d x d p = –4 x p ⇒ p d p = – x 2 + 1 4 x d x ⇒ ∫ p d p = –2 ∫ x 2 + 1 d ( x 2 + 1 ) ⇒ ln ∣ p ∣ = –2 ln ( x 2 + 1 ) + ln C 1 ⇒ ln ∣ p ∣ = ln ( x 2 + 1 ) 2 C 1 ⇒ p = ( x 2 + 1 ) 2 C 1
با بدست آمدن p p p z z z
p = z ′ = C 1 ( x 2 + 1 ) 2 ⇒ z = ∫ d x ( x 2 + 1 ) 2 \large {p = z ^ { \prime } = \frac { { { C _ 1 } }} { { { { \left ( { { x ^ 2 } + 1 } \right ) } ^ 2 } } } \ } \Rightarrow { z = \int { \frac { { d x } } {{ { { \left ( { { x ^ 2 } + 1} \right ) } ^ 2 } } } } } p = z ′ = ( x 2 + 1 ) 2 C 1 ⇒ z = ∫ ( x 2 + 1 ) 2 d x
نحوه محاسبه انتگرال توابع کسری را پیشتر توضیح داده بودیم. حاصل این انتگرال به صورت زیر بدست خواهد آمد.
∫ d x ( x 2 + 1 ) 2 = x 2 ( x 2 + 1 ) + 1 2 ∫ d x x 2 + 1 = x 2 ( x 2 + 1 ) + 1 2 arctan x + C 2 \large \begin {align*} \int {\frac { { dx }} { { { {\left( { { x ^ 2 } + 1} \right ) } ^ 2 } } } } &= { \frac { x } { { 2 \left( { { x ^ 2} + 1} \right ) } } } + { \frac { 1 } { 2 } \int { \frac { { d x } } { { { x ^ 2 } + 1 } } } } \\ & = { \frac { x } { { 2 \left ( { { x ^ 2 } + 1 } \right ) } } } + { \frac { 1 } { 2 } \arctan x } + { { C _ 2 } } \end {align*} ∫ ( x 2 + 1 ) 2 d x = 2 ( x 2 + 1 ) x + 2 1 ∫ x 2 + 1 d x = 2 ( x 2 + 1 ) x + 2 1 arctan x + C 2
در نتیجه تابع z z z
z = C 1 [ x 2 ( x 2 + 1 ) + 1 2 arctan x + C 2 ] = C 1 x x 2 + 1 + C 1 arctan x + C 2 \large \begin {align*} z & = { C _ 1 } \left[ { \frac { x } { { 2 \left ( { { x ^ 2 } + 1} \right ) } } } \right. + \left. { \frac { 1 } { 2 } \arctan x + { C _ 2 } } \right] \\ & = { \frac { { { C _ 1 } x } } { { { x ^ 2 } + 1} } } + { { C _ 1 } \arctan x } + { { C _ 2 } } \end {align*} z = C 1 [ 2 ( x 2 + 1 ) x + 2 1 arctan x + C 2 ] = x 2 + 1 C 1 x + C 1 arctan x + C 2
بنابراین نهایتا تابع y y y
y = ( x 2 + 1 ) z = C 1 x + C 1 ( x 2 + 1 ) arctan x + C 2 ( x 2 + 1 ) = C 1 [ x + ( x 2 + 1 ) arctan x ] + C 2 ( x 2 + 1 ) \large \begin {align*} y & = \left ( { { x ^ 2 } + 1} \right ) z \\ & = { { C _1 } x } + { { C _ 1 } \left ( { { x ^ 2 } + 1} \right ) \arctan x } + { { C _ 2 } \left ( { { x ^ 2 } + 1} \right) } \\ & = { { C _ 1 } \left [ {x + \left ( { { x ^ 2 } + 1 } \right ) \arctan x } \right] } + { { C _ 2 } \left ( { { x ^ 2 } + 1 } \right ) } \end {align*} y = ( x 2 + 1 ) z = C 1 x + C 1 ( x 2 + 1 ) arctan x + C 2 ( x 2 + 1 ) = C 1 [ x + ( x 2 + 1 ) arctan x ] + C 2 ( x 2 + 1 )
مثال ۶
پاسخ عمومی معادله x 2 y ′ ′ – 4 x y ′ + 6 y = 0 { x ^ 2 } y ^ { \prime \prime } – 4 x y ^ { \prime } + 6 y = 0 x 2 y ′′ –4 x y ′ + 6 y = 0 y 1 = x 2 { y _ 1 } = { x ^ 2 } y 1 = x 2
به منظور پاسخ به این سوال در ابتدا y 1 y_1 y 1 y 2 y_2 y 2
$$ \large {\begin {align*} W \left( x \right) & = {W_{{y_1},{y_2}}}\left( x \right)<br />
= {\left| {\begin{array}{*{20} { c } } { { y _1 } } & { { y _2 } } \\<br />
{ { y ^ { \prime }_1}}& { { y ^ { \prime } _ 2 } } \end {array} } \right| } \\ & = { { W _ 0 } \left ( x \right)\exp \left( { – \int \limits _ {{ x _ 0 } } ^ x { \frac { { { a _1 } \left( t \right ) } } { { {a _ 0 } \left ( t \right ) } } d t } } \right ) } \end {align*}} $$
حاصل انتگرال موجود در رابطه فوق نیز به صورت زیر بدست خواهد آمد.
∫ x 0 x a 1 ( t ) a 0 ( t ) d t = ∫ x 0 x ( – 4 t t 2 ) d t = ( – 4 ln t ) ∣ x 0 x = – 4 ln x + 4 ln x 0 = – ln x 4 + ln x 0 4 = – ln x 4 x 0 4 \large \begin {align*} \int\limits _ { { x_0 } } ^ x { \frac { { {a _ 1 } \left( t \right)}}{{{a_0}\left( t \right ) }} d t } & = { \int \limits _ { { x _ 0 } } ^ x { \left ( { \frac { { – 4 t } } { { { t ^ 2} } } } \right)dt} } \\ & = {\left. {\left( { – 4 \ln t } \right ) } \right|_ { { x _0 } } ^ x } \\ & = { – 4\ln x + 4 \ln { x _ 0 } } \\ & = { – \ln { x ^ 4 } + \ln x_0^4 } = { – \ln \frac { { { x ^ 4 }} } { { x _0 ^ 4 } } } \end {align*} x 0 ∫ x a 0 ( t ) a 1 ( t ) d t = x 0 ∫ x ( t 2 –4 t ) d t = ( –4 ln t ) ∣ x 0 x = –4 ln x + 4 ln x 0 = – ln x 4 + ln x 0 4 = – ln x 0 4 x 4
بنابراین رونسکین نیز به صورت زیر بدست خواهد آمد.
$$ \large \begin {align*} {\left| {\begin{array}{*{20}{c}} { { y _ 1 } } & { { y _2 } } \\<br />
{{y ^ { \prime } _ 1 } } & { { y ^{\prime} _ 2 } } \end{array}} \right| } & = {{W_0}\left( x \right)\exp \left ( {\ln \frac { { { x ^ 4} } } {{ x _0 ^ 4 } } } \right) } \\ & = { \frac { { { W_0}\left( x \right)}}{{x_0^4}}{ x ^ 4 } } = { { C _1 } { x ^ 4 } } \end {align*} $$
با توجه به اینکه y 1 y_1 y 1 y 2 y_2 y 2
$$\large \require {cancel} \begin {align*} \left. { { y ^ { \prime } _ 2 } { y_ 1 } – { y _2 } { y ^ { \prime } _ 1 } = { C _ 1 } { x ^ 4 } } \right|:y _ 1 ^ 2 \ \\~\\ \Rightarrow {\frac { { { y ^ { \prime } _2 } { y _ 1 } – { y _2 } { y ^ { \prime } _ 1} } } { { y _ 1 ^ 2} } = \frac { { {C _ 1 } { x ^4 } } } { {y _ 1 ^ 2 } } } \\~\\ \Rightarrow { { \left( {\frac { { { y _ 2 } } } { { { y_ 1 } } } } \right ) ^ \prime } } = {\frac { {{ C _ 1 } { x^ 4 } } } { { y _ 1 ^ 2 } } } = { \frac { { { C _ 1 } \cancel { x ^ 4}} } { { \cancel { x ^ 4 }} } } = { { C _ 1 } } \end {align*} $$
در نتیجه تابع y 2 y_2 y 2
y 2 y 1 = C 1 x + C 2 ⇒ y 2 = y 1 ( C 1 x + C 2 ) x 2 ( C 1 x + C 2 ) = C 1 x 3 + C 2 x 2 \large \begin {align*} \frac { { { y_ 2 } } } { { { y _ 1 } } } & = {C_1}x + {C_2} \;\; \Rightarrow { y _ 2 } \\ & = { y _ 1 } \left ( { { C _1 } x + { C _ 2 } } \right ) { { x ^ 2 } \left ( { { C_ 1 } x + { C _ 2 } } \right ) } \\ & = { { C_ 1 } { x ^ 3 } + { C _ 2 }{ x ^2 } } \end {align*} y 1 y 2 = C 1 x + C 2 ⇒ y 2 = y 1 ( C 1 x + C 2 ) x 2 ( C 1 x + C 2 ) = C 1 x 3 + C 2 x 2
همانطور که میبینید تابع y 2 y_2 y 2 y 1 y_1 y 1 y 2 y_2 y 2
مثال ۷
پاسخ عمومی معادله x 2 y ′ ′ + x y ′ – y = 0 \begin {align*} { x ^ 2} y ^ { \prime \prime } + x y ^ { \prime } – y = 0 \end {align*} x 2 y ′′ + x y ′ – y = 0 y 1 = x { y _ 1 } = x y 1 = x
در ابتدا فرمول لیوویل را به صورت زیر مینویسیم.
$$ \large { W \left( x \right) = { W _ {{ y _ 1 } , { y _ 2} } } \left( x \right) }<br />
= {\left| {\begin{array}{*{20} { c } } { { y _ 1} } & { {y _ 2 } } \\<br />
{{ y ^{\prime} _ 1 } } &{{y ^ { \prime } _2 } } \end{array}} \right| } = {{C_1}\exp \left( { – \int {\frac{{{a_1}\left( x \right) } } { { { a_ 0 }\left( x \right ) } }d x } } \right) } $$
از طرفی انتگرال موجود در این فرمول نیز برابر خواهد بود با:
∫ a 1 ( x ) a 0 ( x ) d x = ∫ x x 2 d x = ∫ d x x = ln ∣ x ∣ \large \begin {align*} \int { \frac { { {a _1 } \left ( x \right ) } } {{ { a _ 0 } \left( x \right) } } d x } & = {\int {\frac { x }{ { { x ^ 2 } } } d x } } \\ & = { \int { \frac { { d x } } { x } } } = {\ln \left| x \right| } \end {align*} ∫ a 0 ( x ) a 1 ( x ) d x = ∫ x 2 x d x = ∫ x d x = ln ∣ x ∣
در نتیجه معادله مد نظر برای بدست آوردن y 2 y_2 y 2
y 2 ′ y 1 – y 2 y 1 ′ = C 1 e – ln ∣ x ∣ ⇒ y 2 ′ y 1 – y 2 y 1 ′ = C 1 e ln 1 ∣ x ∣ ⇒ y 2 ′ y 1 – y 2 y 1 ′ = C 1 x \large \begin {align*} { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2} { y ^ { \prime } _ 1 } = { C _ 1 } { e ^ { – \ln \left| x \right| } } & \Rightarrow { { y ^ { \prime } _2}{y_1} – { y _ 2 } { y ^ { \prime } _1} = { C _1 } { e ^ { \ln \large\frac{1}{ { \left| x \right| } } \normalsize } }} \\ & \Rightarrow { { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2 } { y ^{\prime} _ 1 } = \frac { { { C_ 1 } } } { x } } \end {align*} y 2 ′ y 1 – y 2 y 1 ′ = C 1 e – l n ∣ x ∣ ⇒ y 2 ′ y 1 – y 2 y 1 ′ = C 1 e l n ∣ x ∣ 1 ⇒ y 2 ′ y 1 – y 2 y 1 ′ = x C 1
با تقسیم کردن طرفین رابطه فوق به y 1 2 = x 2 y _ 1 ^ 2 = { x ^ 2 } y 1 2 = x 2
y 2 ′ y 1 – y 2 y 1 ′ y 1 2 = C 1 x y 1 2 ⇒ ( y 2 y 1 ) ′ = C 1 x ⋅ x 2 = C 1 x 3 ⇒ y 2 y 1 = ∫ C 1 x 3 d x = – C 1 2 x 2 + C 2 = C 1 x 2 + C 2 \large \begin {align*} {\frac { { { y ^{\prime} _ 2 } { y _ 1 } – {y_2}{y^{\prime}_1}}}{ { y_ 1 ^ 2 } } = \frac{{{C_ 1 } } } { { x y _ 1^ 2 } } } & \Rightarrow { { \left ( { \frac { { {y_2 } }} { { { y _ 1 } } } } \right)^\prime } = \frac{{ { C_ 1 } } } { {x \cdot { x ^ 2 } } } = \frac{{ { C _1 } }} {{{ x ^ 3} } } } \\ & \Rightarrow {\frac { { {y _ 2} } } { { { y _1 } } } = \int {\frac { { { C_ 1 } } } { {{ x ^ 3 }}} d x} } = { – \frac { { { C_ 1 } } } {{ 2 { x ^2 } } } + {C_2} }={ \frac { { {C _1 } } } { {{ x ^ 2 } }} + {C _ 2 } } \end {align*} y 1 2 y 2 ′ y 1 – y 2 y 1 ′ = x y 1 2 C 1 ⇒ ( y 1 y 2 ) ′ = x ⋅ x 2 C 1 = x 3 C 1 ⇒ y 1 y 2 = ∫ x 3 C 1 d x = – 2 x 2 C 1 + C 2 = x 2 C 1 + C 2
در این مرحله ثابتِ − C 1 2 - \frac { C _ 1 } { 2 } − 2 C 1 C 1 C_1 C 1 – C 1 2 → C 1 – { \large \frac { { { C _ 1 } } } { 2 } \normalsize} \to { C _ 1 } – 2 C 1 → C 1
y 2 = y 1 ( C 1 x 2 + C 2 ) = x ( C 1 x 2 + C 2 ) = C 1 x + C 2 x \large \begin {align*} { y _ 2 } = {y_1}\left( {\frac { { {C _ 1 } }} { {{ x ^2 } } } + { C _ 2} } \right) & = { x \left( {\frac { { { C _1 } } } {{ { x ^2 } } } + { C _2 } } \right ) } \\ & = { \frac { { { C _ 1} } } { x } + { C _ 2 } x } \end {align*} y 2 = y 1 ( x 2 C 1 + C 2 ) = x ( x 2 C 1 + C 2 ) = x C 1 + C 2 x
فیلم های آموزش معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر – از صفر تا صد (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی رونسکین فیلم آموزشی تشکیل معادله دیفرانسیل با داشتن جوابهای پایه فیلم آموزشی حل معادله دیفرانسیل همگن مرتبه دو فیلم آموزشی حل چند مثال از معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر