روش های مشتق گیری – به همراه مثال
پیشتر در وبلاگ فرادرس و در مطلبی تحت عنوان مفاهیم مشتق، به معرفی این مفهومِ مهم از ریاضیات پرداختیم. در این مطلب از مجله فرادرس قصد داریم تا در مورد قوانین حاکم بر مشتق گیری صحبت کنیم و مثالهایی نیز از کاربرد این قوانین ارائه خواهیم داد. این قوانین هم در محاسبه مشتق ضمنی و هم در محاسبه مشتق صریح کاربرد خواهند داشت.


قوانین حاکم در مشتق گیری
برای محاسبه راحتتر مشتق، قوانینی وجود دارند که میتوان از آنها استفاده کرد. برای نمونه شیب یک تابع ثابت برابر با صفر است. یا اینکه شیب تابع 2x برابر با ۲ و تابع 3x برابر با ۳ است. این استدلال را میتوان به همین شکل ادامه داد و گفت شیب تابع nx برابر با n است.
در نمودارهای زیر میتوانید شیب مرتبط با هر کدام از این توابع را مشاهده کنید.

در بخش مفاهیم مشتق، جداولی را ارائه دادیم که قادریم با استفاده از قوانین معرفی شده در آنها، مشتق گیری بسیاری از توابع را انجام دهیم. این جداول به صورت زیر هستند.
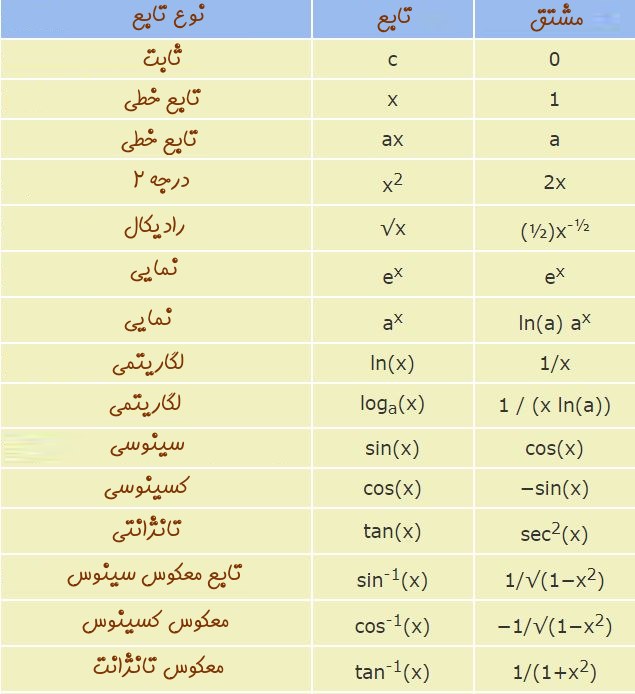
جدول بالا نشان دهنده مشتق توابع مختلف است. اگر دقت کنید همواره میتوان الگویی را برای این مشتقات مشخص کرد. برای نمونه میتوان از جدول این استدلال را کرد که توابع سینوس و کسینوس در مشتق گیری به یکدیگر تبدیل میشوند. یا اینکه یک تابع نمایی خودش را تکرار میکند. یافتن این الگوها در به خاطر سپردن مشتق یک تابع، بسیار موثر است. البته در مطلبی جداگانه در مجله فرادرس مشتق توابع لگاریتمی و نمایی توضیح داده شده است.
از طرفی میتوان این سوال را مطرح کرد که آیا با دانستن مشتق تابع sin x و cos x، میتوان مشتق تابع f(x)=sinx × cosx را یافت؟ پاسخ این سوال مثبت است. با استفاده از قوانینی که در جدول زیر ارائه شدهاند میتوان مشتق هر تابعی را محاسبه کرد.
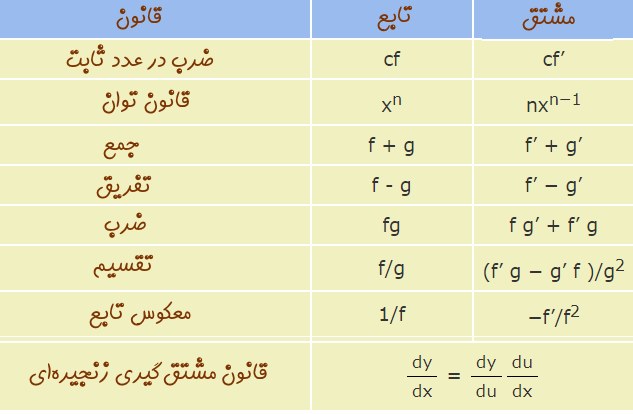
لطفا موارد ذکر شده در جدول بالا را به دقت مطالعه فرمایید، چرا که در مثالهای پایین از آنها استفاده خواهیم کرد.
توجه داشته باشید که مشتق تابع (y=f(x را به یکی از شکلهای زیر نشان میدهند.
روشهای نشان دادن مشتق یک تابع
در مثالی که در ادامه آمده، ادبیات استفاده شده در فرآیند مشتق گیری را بیان خواهیم کرد. همچنین روشهای نشان دادن مشتق یک تابع ارائه خواهد شد.
مثال ۱: مشتق تابع (y=sin (x ؟
در جدول بالا بیان شده که مشتق تابع sin x برابر با cos x است. توجه داشته باشید که میتوان این عملیات را به شکلهای زیر نشان داد.
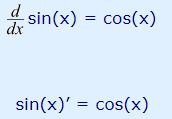
استفاده از قانون توانی در محاسبه مشتق
قانون توانی در محاسبه مشتق بیان میکند که مشتق تابع xn برابر با nxn-1 است.
مثال ۲: مقدار عبارت را محاسبه کنید
این عبارت بیان کننده مشتق تابع x3 نسبت به متغیر x است. با استفاده از قانون توانی، میتوان مشتق تابع مذکور را به شکل زیر محاسبه کرد:
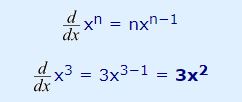
بنابراین میتوان گفت: «مشتق تابع x3 برابر با 3x2 میشود.» در ادامه شماتیک نحوه محاسبه این مشتق نمایش داده شده.
مثال ۳: مشتق تابع را بدست آورید
این تابع در حقیقت برابر با f(x)=x-1 است. بنابراین میتوان با استفاده از قانون توان، حاصل این مشتق را محاسبه کرد. از این رو میتوان گفت:
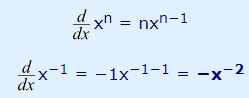
در حقیقت برای محاسبه این مشتق، به ترتیب زیر عمل کردهایم.
محاسبه مشتق تابعی با ضریب ثابت
همانطور که احتمالا حدس زدهاید، بهمنظور محاسبه مشتق تابعی که در عددی ثابت ضرب شده، میتوان عدد مذکور را از عملگر مشتق بیرون کشید. یعنی فرض کنید تابعی به صورت زیر داشته باشیم.
که در آن، c ضریبی ثابت و (f(x یک تابع است.
با این فرضیات مشتق این تابع برابر با مقدار زیر است.
برای نمونه مشتق (5f(x برابر با 5f'x است.
مثال 4: مشتق را بدست آورید
برای محاسبه این مشتق در ابتدا ضریب ثابت ۵ را بیرون کشیده و پس از آن با استفاده از قانون توان، مشتق x3 را محاسبه میکنیم. بنابراین میتوان گفت:
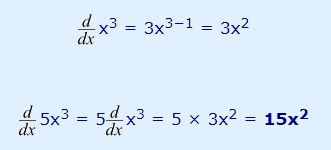
قانون جمع و تفریق
دو تابع (f(x و (g(x را تصور کنید. فرض کنید میخواهیم مشتق تابع (f(x)+g(x را بیابیم. برای انجام اینکار از هر کدام از این توابع به تنهایی مشتق گرفته و سپس با یکدیگر جمع میکنیم. بنابراین میتوان گفت:
مشتق { f(x)+g(x) } = مشتق f + مشتق g
و یا به بیان ریاضیاتی:
مثال 5: مشتق x2+x3 برابر با چه تابعی است؟
همانطور که در بالا نیز بیان کردیم، برای محاسبه مشتق جمع دو تابع، از هر کدام از آنها مشتق گرفته و با یکدیگر جمع میکنیم. همانطور که در عنوان مثال نیز میبینید، دو تابعی که با یکدیگر جمع شدهاند، به شکل توانی هستند؛ بنابراین در ابتدا بایستی با استفاده از قانون توان، مشتق هر کدام از آنها را محاسبه کرد. در نتیجه با استفاده از این قانون و قانون جمع میتوان حاصل این مشتق را به شکل زیر محاسبه کرد.

بر همین مبنا میتوان مشتق توابعی که از یکدیگر کم شدهاند را نیز بدست آورد. برای درک بهتر به مثال زیر توجه فرمایید.
مثال 6: حاصل عبارت را بیابید.
توجه داشته باشید که متغیر وابسته یک تابع را به هر اسمی میتوان صدا زد. برای مثال ما میگوییم گربه و در استرالیا به همین موجود Cat گفته میشود! در این مثال نیز اتفاق خاصی نیفتاده و فقط به جای اسم x از v استفاده شده.
مشابه با قانون جمع، به منظور محاسبه مشتق تفریق دو تابع، میتوان از هر کدام از آنها مشتق گرفت و از هم کم کرد. بنابراین مشتق این تابع به صورت زیر محاسبه میشود:
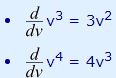
حال میتوان به شکل زیر این مشتقات را از یکدیگر کم کرد. در نتیجه:
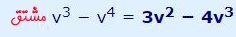
مثال 7: حاصل عبارت را بیابید.
برای محاسبه عبارت بالا میتوان از قوانین بیان شده استفاده کرد. بنابراین با استفاده از قوانین توان، ضریب ثابت، جمع و تفریق داریم:
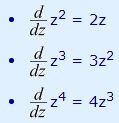
در نتیجه مشتق این تابع برابر است با:
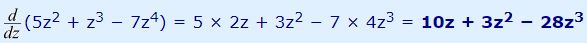
قانون ضرب
به جرأت یکی از پرکاربردترین قوانین، بهمنظور محاسبه مشتق توابع، قانون ضرب است. برای درک مفهوم این قانون، دو تابع (f(x و (g(x را فرض کنید. هدف ما محاسبه مشتق تابع (f(x)×g(x است. قانون ضرب، بیان میکند:
(f×g) مشتق تابع = f مشتق تابع × g + g مشتق تابع × f
به بیان ریاضی، گذاره بالا معادل است با:
مثال 8: حاصل مشتق تابع (sin(x)cos(x چیست؟
در ابتدا بایستی مشتق هر کدام از دو تابعی که در هم ضرب شدهاند را به صورت جداگانه محاسبه کرد. بنابراین میتوان گفت:
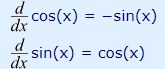
در نتیجه با استفاده از رابطه * میتوان گفت:
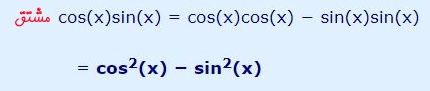
قانون عکس تابع
تابع (f(x را تصور کنید. فرض کنید میخواهیم مشتق تابع را محاسبه کنیم. این مشتق را میتوان با استفاده از قانون عکسِ تابع و به صورت زیر محاسبه کرد.

در مطلب مشتق ضمنی در مجله فرادرس نیز روشی ارائه خواهد شد که با استفاده از آن میتوانید مشتق توابع معکوس را بهصورتی بسیار سادهتر بدست آورید.
مثال 9: مشتق تابع را بیابید.
این تابع در حقیقت عکس sin x است. در نتیجه در ابتدا بایستی مشتق تابع sin x را داشته باشیم. سپس با استفاده از قانون عکس تابع، مشتق را یافت. با توجه به اطلاعات جدول، مشتق تابع sin x برابر با cos x است. در نتیجه با استفاده از این قانون داریم:
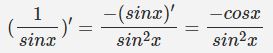
قانون مشتق گیری زنجیرهای
تابع (g(x و (f(x را در نظر بگیرید. تصور کنید میخواهیم مشتق ( (f( g(x را محاسبه کنیم. قانون مشتق گیری زنجیرهای بیان میکند که مشتق این تابع برابر است با:

مشتق تابع ((f(g(x را میتوان بترتیب مراحل زیر محاسبه کرد:
۱. مشتق تابع (g(x را محاسبه کنید.
۲. در تابع ( (f (g(x به جای (g(x، متغیر وابسته را قرار دهید و مشتق گیری کنید.
۳. در تابع بدست آمده در قدم دوم، به جای متغیر وابسته، تابع (g(x را قرار دهید.
۴. عبارت حاصل شده در مرحله سوم را در عبارت بدست آمده در قدم اول، ضرب کنید.
بهمنظور درک بهتر مشتق گیری زنجیرهای، به مثالی که در ادامه آمده توجه فرمایید.
مثال 10: حاصل عبارت چیست؟
اگر دقت کنید این تابع حاصل قرار گرفتن x2 در sin x است. بنابراین اگر تابع f(x)=sin x و g(x)=x2 در نظر بگیریم، میتوان گفت:
f(g(x))=sin (x2)
مراحل بالا را برای مشتق گیریِ تابع ( (f ( g(x، به شکل زیر پیاده سازی میکنیم:
۱. مشتق گیری از تابع (g(x
تابع داخلی برابر با g(x)=x2 است. بنابراین مشتق آن برابر با g'(x)=2x است.
۲. به جای تابع (g(x، متغیر وابسته - که در اینجا x است - قرار دهید و مشتق گیری کنید.
با قرار دادن x به جای (g(x، عبارت sin x حاصل شده و با مشتق گیری از آن به تابع cos x میرسیم.
۳. در تابع بدست آمده در قدم دوم، به جای متغیر وابسته، تابع درونی را قرار دهید.
در قدم دوم، تابع cos x بدست آمد. بنابراین با قرار دادن g(x)=x2 به جای x در تابعِ cos x، عبارت (cos (x2 حاصل میشود.
۴. تابع حاصل شده در مرحله سوم را در عبارت بدست آمده در قدم اول ضرب کنید.
با ضرب تابع بدست آمده در مرحله سوم و تابع بدست آمده در مرحله اول، به تابع (2xcos(x2 میرسیم.
بنابراین نهایتاً میتوان گفت:
مشتق گیری زنجیرهای تکنیکی کاربردی بهمنظور حل بسیاری از مسائل مربوط به مشتق است که با تمرین بسیار میتوانید به این روش مسلط شوید. در ادامه مثالی به نسبت مشکلتر را مطرح کردهایم.
مثال ۱1: مشتق تابع را بیابید.
اگر دقت کنید این تابع متشکل از دو تابع cosx و است. در حقیقت اگر f(x)=1/x و g(x)=cos x باشد، تابع ((f(g(x برابر با میشود.
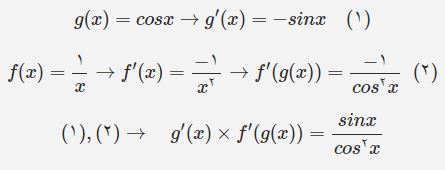
مثال ۱2: مشتق تابع برابر با چه مقداری است؟
قبل از مطالعه ادامه حل در مورد اینکه f و g چه هستند، فکر کنید. بله درست حدس زدید تابع f برابر با x3 و تابع g برابر با 5x-2 هستند. در نتیجه مشتق این تابع برابر است با:
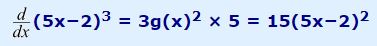
به منظور ارزیابی خود میتوانید به سوالات زیر پاسخ دهید.
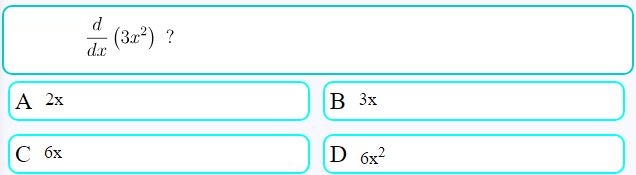

آزمون روش های مشتق گیری
۱. کدام گزینه قانون توانی را برای مشتقگیری از تابع x به توان n بیان میکند؟
مشتق همیشه یک عدد ثابت برابر با n است.
مشتق برابر x تقسیم بر n به توان n منهای یک است.
مشتق برابر n ضربدر x به توان n منهای یک است.
مشتق برابر n تقسیم بر x به توان n است.
عبارت «مشتق برابر n ضربدر x به توان n منهای یک است» همان فرمولی است که به عنوان قانون توانی ارائه شده است و طبق متن مشتق $$ $$ x^n $$ $$ را با تعریف میکند.
۲. در مشتقگیری توابع ترکیبی، چه تفاوتی میان قانون قانون ضرب و قاعده زنجیرهای وجود دارد؟
هیچ تفاوت کارکردی بین این دو قانون وجود ندارد و همیشه به صورت یکسان استفاده میشوند.
قانون ضرب صرفا برای جمع و تفریق توابع استفاده میشود و قاعده زنجیرهای برای هر ضرب به کار میرود.
هر دو قانون فقط برای مشتق توابع کسری قابل استفادهاند و ساختار خاصی ندارند.
قانون ضرب زمانی استفاده میشود که دو تابع به صورت حاصلضرب در هم باشند، اما قاعده زنجیرهای برای توابع پیچیده به کار میرود.
هنگامی که دو تابع در هم ضرب شوند (مانند ) باید از قانون ضرب استفاده کرد و هر تابع را جداگانه مشتق گرفت و طبق فرمول ترکیب کرد. اما اگر تابعی به صورت تو در تو باشد (مانند )، لازم است از قاعده زنجیرهای بهره برد که مشتق تابع بیرونی و ضرب آن در مشتق تابع درونی را به کار میبرد.
۳. برای مشتقگیری تابع کدام شیوه با توجه به قوانین پایه مشتقگیری صحیح است؟
ضریب ثابت را حذف کرده و فقط قسمت توانی را مشتق بگیریم.
کل تابع را مشابه یک عبارت توانی مشتق بگیریم.
هر جزء را جداگانه مشتق بگیریم و سپس جمع کنیم.
اول مشتقگیری از و بعد ضرب در کل تابع
در تابع باید بر اساس قانون جمع و نیز قانون ضرایب ثابت، مشتق هر جزء را جدا محاسبه کنیم و سپس نتایج را با هم جمع کنیم. این روش مطابق قواعد اولیه مشتق برای توابع جمعی و ضرب در عدد ثابت است.
۴. در مشتقگیری از عبارتی مانند چرا رعایت استفاده ترکیبی از چند قانون مشتق اهمیت دارد؟
صرفا استفاده از جدول مشتقات پایه بدون ترکیب کافی است.
فقط کافی است قانون جمع را روی همه عبارتها استفاده کنیم.
چون برای هر جزء باید قانون مربوط به آن مانند ضرب، توان و جمع را به صورت همزمان بکار برد.
زیرا هر تابع باید جداگانه فقط با قانون توانی مشتق شود.
در حالتی مثل اگر فقط یک قانون مانند قانون توانی یا فقط جمع اجرا شود، مشتق هر جزء بدرستی به دست نمیآید. بخش نیازمند قانون ضرب و بخش به قانون توانی و جمع به کارگیری همزمان آنها است.













مشتق f(x)=x به توان n اثبات فرمولش چی میشه
با سلام خدمت شما همراه گرامی؛
ابتدا از تعریف اصلی مشتق یعنی حد کسر تغییرات hf(x+h)−f(x) شروع میکنیم. حالا عبارت (x+h)n را با استفاده از بسط دو جملهای خیام – نیوتن باز میکنیم. در صورت کسر، xnهای مثبت و منفی حذف میشوند. سپس از تمام جملات باقیمانده در صورت، یک h فاکتور گرفته و با مخرج ساده میکنیم. پس از سادهسازی، فقط جمله اول یعنی nxn−1 فاقد h است و بقیه جملات h دارند که با میل کردن h به سمت صفر، تمام جملات دارای h حذف میشوند و در نهایت فرمول nxn−1 بهدست میآید.
از بازخورد و همراهی شما با مجله فرادرس سپاسگزاریم.
با تشکر از زحمات شما عزیزان
حدود ۳۰سال قبل درسهای دبیرستان را تمام کرده بودم و همان سال در رشته عمران (کارشناسی) قبول شدم و تا امروز که همه مطالب برایم یادآوری شد
بسیار عالی اطلاعات دسته بندی شده و مثالهای خوبی حل شده
با تشکر
فرادرس بی رقیب?
واقعا ممنونم
خیلی خیلی ممنونم
خیلی خیلی خیلی ممنونم:)))
شیر مادر نان پدر حلالت باشع❤️❤️❤️♥️♥️😊
وای مرسی مرسییی مرسییییی مرسییییییی
چطوری از قدر مطلقی که درونش متغیر وجود دارد مشتق بگیریم؟
باید تعیین علامت کنی اگه مثبت شد از عبارت داخلش مشتق می گیری اگه منفی شد از قرینه عبارت داخل قدر مطلق مشتق بگیر.
مشتق رادیکال۲تقسیم بررادیکالLچند میشه؟
من از مطالب آموزشی شما نهایت بهره رو بردم،برای دکتری اقتصاد.
خدا بهتون عوض این نیکی رو بده.
با آرزوی موفقیت و شادکامی
مشتق رادیکال۲تقسیم بررادیکالL را دقیقتر توضیح بدین که چطوری محاسبه کردین؟؟ چون من جواب -1/√2(L^3/2) حساب کردم. منفی یک تقسیم بر رادیکال 2 در L به توان سه دوم. خواهشا بگید چه قوانینی را بکار بردین. بسیار ممنونم.
سلام. این عبارت به صورت زیر محاسبه میشود:
f=L2=L212=2L−21⇒f’=2(−21)L−21−1=−22L−23=−2L232=−2L32
از همراهیتان با مجله فرادرس خوشحالیم.
کاش اثبات قوانین رو هم میذاشتید
درس بسیار ارزشمندی بود. سپاسگزارم.
سلام مشتق y=1/4x^2 -x چند میشه؟
سلام خسته نباشید میشه لطفا این عبارت رو حل کنید؟
Xsin(xy-y²) +1=x²
مشتق رو خواسته
مشتق lnرادیکال x^2 چی میشه؟
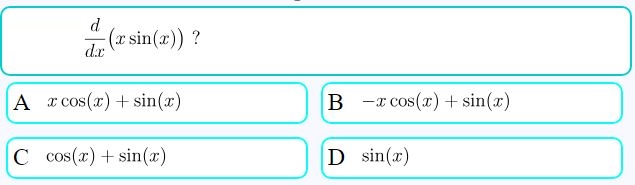
سلام مشتق (x sin(x چند می شه؟؟
مرسی از سایت خوبتون
سلام.
همانگونه که در این آموزش اشاره شده است، مشتق xsin(x) با استفاده از قاعده مشتق ضرب دو تابع، برابر با sin(x)+xcos(x) است.
موفق باشید.
سلام
مشتق [x]x رو نگفتید
اصلا مشتق براکت چحوریه
یا مشتق براکت ایکس به توان دو؟
فرمول مشتق(sin(uبه صورت (u’cos(u
است که جواب شما
sin2x=2cos2x
سلام ممنون از مطالب خوبتون،مشتق sin2x و چه جوری باید حساب کرد؟
مشتق داخل سینویس ضرب در مشتق خود سینوس بدون در نظر گرفتن داخلش
2*cos2x
مشتق ۴ پی به توان ۲ چی میشه؟
اگر منظور از پی 3/14…. است پس یک عدد است نه متغیر که به توان رسیده و مشتق عدد ثابت صفر است.
سلام مشتق sin² چند می شه ؟
= 2 sin(x) cos(x)
سلام. مشتق تابع sin2x برابر با 2sinx است.
سلام میشه بگید (مشتق سینوس توان 2 داخل پرانتز پی ششم بعلاوه ایکس دوم) چند می شود؟
با سلام و ممنون از بازخورد ارائه شده. در تصویر زیر این مشتق بدست آمده است.
واقعا استفاده کردم
ممنون و متشکرم
واقعا عالی بود ،کاملا فراموشم شده بود ،عالی آموزش داده شد